推导部分和——带权并查集

题解:
带权并查集
引言: 带权并查集是一种进阶的并查集,通常,结点i的权值等于结点i到根节点的距离,对于带权并查集,有两种操作需要掌握——Merge与Find,涉及到路径压缩与维护权值等技巧。
带权并查集的数据结构
-
使用顺序存储结构,定义结构体数组,其中a[i]的root代表节点 i 的根节点编号,weight代表它与root号节点之间的距离,也就是权值。
struct node {int root;ll weight;node() :root(0), weight(0) {} }a[100005];
Find函数+权值合并
-
首先,在执行整个并查集算法之前,需要首先初始化每一个结点的根节点编号为它本身,意思就是说,每一个结点在初始状态时都被视为一颗单独的并查集树,即:
for (int i = 1; i <= n; i++) {a[i].root = i; } -
当我们想要去查询一个节点的根节点时,调用find函数:
-
传入:想要查询的结点编号x
-
返回: 第x号结点的根节点编号
//路径压缩+权值合并 int find(int x) {if (x != a[x].root) {//更新x的根节点int tmp = a[x].root;a[x].root = find(a[x].root);a[x].weight += a[tmp].weight;}return a[x].root; } -
在函数体内:
- 当结点x的root值为它自己时,即 x == a[x].root 时,直接返回a[x].root
- 否则,递归查找它根节点的根节点
- 在递归之前,使用tmp暂存x当前的根节点编号。这是由于在查找的过程中,我们使用了路径压缩的技巧,使a[x].root被赋值为find函数的返回值,但是在后续的计算中,我们又需要使用到这个旧的a[x].root值。
- 在路径压缩的同时,我们必须要维护权值a[x].weight使其始终等于x号结点到a[x].root号结点的距离。
- 在路径压缩之前,a[x].weight存储的是x到旧的root的距离,但root发生更改后,此时新的权值a[x].weight应该修改为dist(新root,旧root) + dist(旧root,x)才能符合权值的定义,dis(新root, 旧root)将会被递归计算出来,而dis(旧root, x)正是a[x].weight现在存储的值,因此,我们必须要记下旧root的编号才能找到旧root的位置,这也就是tmp发挥的作用。
-
合并
- 当我们得到了两个结点之间的距离,并且想要将这两个结点合并,按照并查集的思想,应当先找到他们各自的根节点,然后再将两颗树合并。然而,我们现在所获取的信息并不是根节点的信息,因此我们需要对已知的信息做一个转化:
-
假设我们现在得到的新的信息是第l-1个节点到第r个节点的距离为w,设第l-1个节点的根节点编号为x,第r个节点的根节点编号为y。
-
首先,我们通过find(l−1)find(l - 1)find(l−1)和find(r)find(r)find(r)获得x与y的值,经过find函数内部的权值维护之后,此时,a[l-1].weight和a[r].weight已经分别被修改为l-1到x和r到y的距离了,设它们分别为w1和w2.

-
通过上图,其实我们很容易就能看出x到y的距离为:w+w2−w1w+w_2-w1w+w2−w1
-
在这,我们只需要算出x到y的距离就好了,在后续调用find函数执行路径压缩和权值合并时将会处理掉它,因此,我们合并的操作就是:
int l, r, w; l = read(), r = read(), w = read(); //x为l-1的根节点,y为r的根节点 int x = find(l - 1), y = find(r); //若l-1与r的根节点不相同 if (x != y) {//将结点x并入y的子树a[x].root = y;//根据向量的思想计算a[x].weight = w + a[r].weight - a[l - 1].weight; }
-
查询
写到这里,这个题目已经接近尾声。(此处再次强调a[i].weight的意义是从第i个节点到第a[i].root个节点的距离,接下来要用的) 当我们维护好了一颗带权并查集树之后,那我们查询区间和就只有两种情况:
- 设区间左端点为l,右端点为r,则
- 当l与r的根不相同时,则无法查询出l到r的区间和。
- 当l与r的根相同时,则有s[l..r]=a[l−1].weight−a[r].weights[l.. r]=a[l-1].weight-a[r].weights[l..r]=a[l−1].weight−a[r].weight
- 以图形的方式表达,蓝色部分即为所求的区间和:

完整代码:
#include <iostream>
#include <cmath>
#include <algorithm>
#define ll long long
using namespace std;
ll n, m, q;//带权并查集结点
struct node {int root;ll weight;node() :root(0), weight(0) {}
}a[100005];
//快读
int read() {char ch = getchar(); int res = 0;while (ch < '0' || ch>'9') {ch = getchar();}while (!(ch < '0' || ch>'9')) {res = res * 10 + (ch - '0');ch = getchar();}return res;
}
//快写
void print(ll x) {if (x > 9) {print(x / 10);}putchar(x % 10 + '0');
}//路径压缩+权值合并
int find(int x) {if (x != a[x].root) {//更新x的根节点int tmp = a[x].root;a[x].root = find(a[x].root);a[x].weight += a[tmp].weight;}return a[x].root;
}int main()
{cin >> n >> m >> q;for (int i = 1; i <= n; i++) {a[i].root = i;}for (int i = 1; i <= m; i++) {int l, r, w;l = read(), r = read(), w = read();//x为l-1的根节点,y为r的根节点int x = find(l - 1), y = find(r);//若l-1与r的根节点不相同if (x != y) {//将结点x并入y的子树a[x].root = y;//根据向量的思想计算a[x].weight = w + a[r].weight - a[l - 1].weight;}}for (int i = 1; i <= q; i++) {int l, r; cin >> l >> r;if (find(l - 1) != find(r)) {puts("UNKNOWN");}else {print(a[l - 1].weight - a[r].weight);putchar('\n');}}return 0;
}
相关文章:

推导部分和——带权并查集
题解: 带权并查集 引言: 带权并查集是一种进阶的并查集,通常,结点i的权值等于结点i到根节点的距离,对于带权并查集,有两种操作需要掌握——Merge与Find,涉及到路径压缩与维护权值等技巧。 带…...
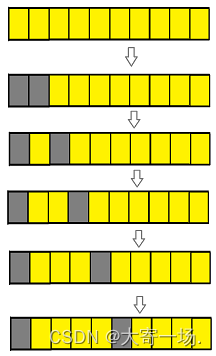
费解的开关/翻硬币
🌱博客主页:大寄一场. 🌱系列专栏: 算法 😘博客制作不易欢迎各位👍点赞⭐收藏➕关注 题目:费解的开关 你玩过“拉灯”游戏吗? 25盏灯排成一个 55 的方形。 每一个灯都有一个开关&…...
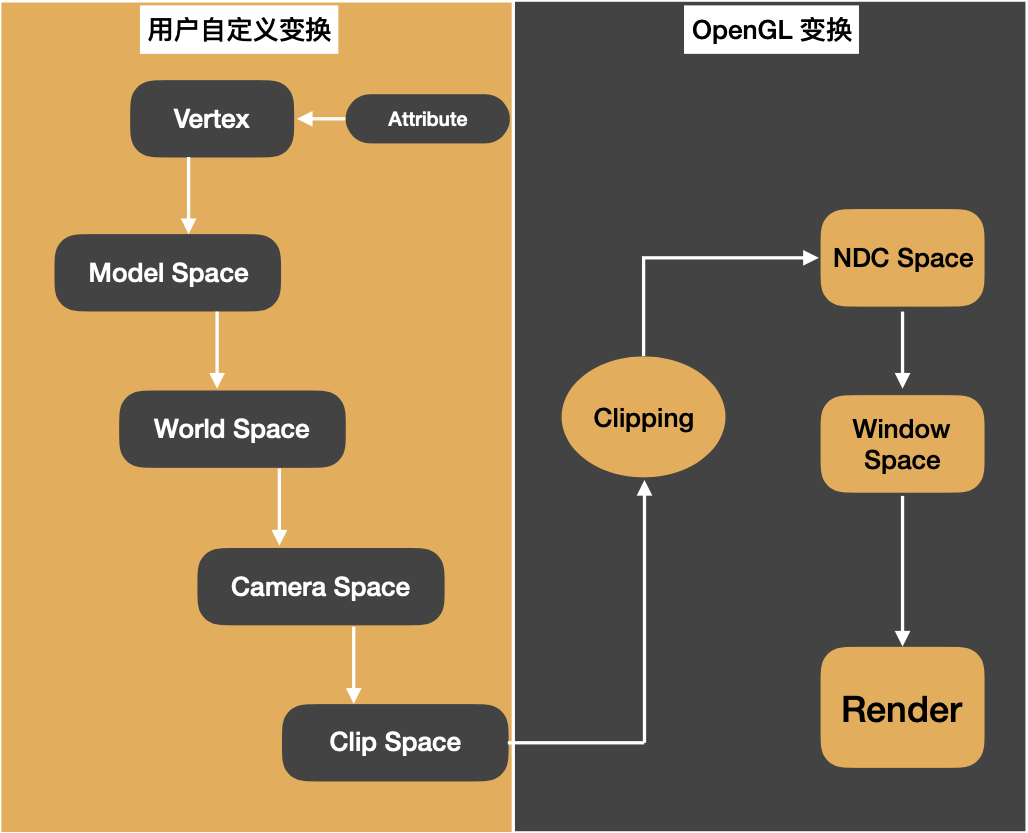
OpenGL中的坐标系
1、2D笛卡尔坐标系2D笛卡尔坐标系跟我们高中的时候学习的坐标系一样,是由x、y决定的。2、3D笛卡尔坐标系3D笛卡尔坐标系坐标由x、y、z决定,满足右手定则。3、视口glViewport(GLint x,GLint y,GLsizei width,GLsizei height)窗口和视口大小可以相同&#…...

Spring——Spring介绍和IOC相关概念
Spring是以Spring Framework为核心,其余的例如Spring MVC, Spring Cloud,Spring Data,Spring Security SpringBoot的基础都是Spring Framework。 Spring Boot可以在简化开发的基础上加速开发。 Spring Cloud分布式开发 Spring有…...

A+B Problem
AB Problem 题目描述 输入两个整数 a,ba, ba,b,输出它们的和(∣a∣,∣b∣≤109|a|,|b| \le {10}^9∣a∣,∣b∣≤109)。 注意 Pascal 使用 integer 会爆掉哦!有负数哦!C/C 的 main 函数必须是 int 类型,…...
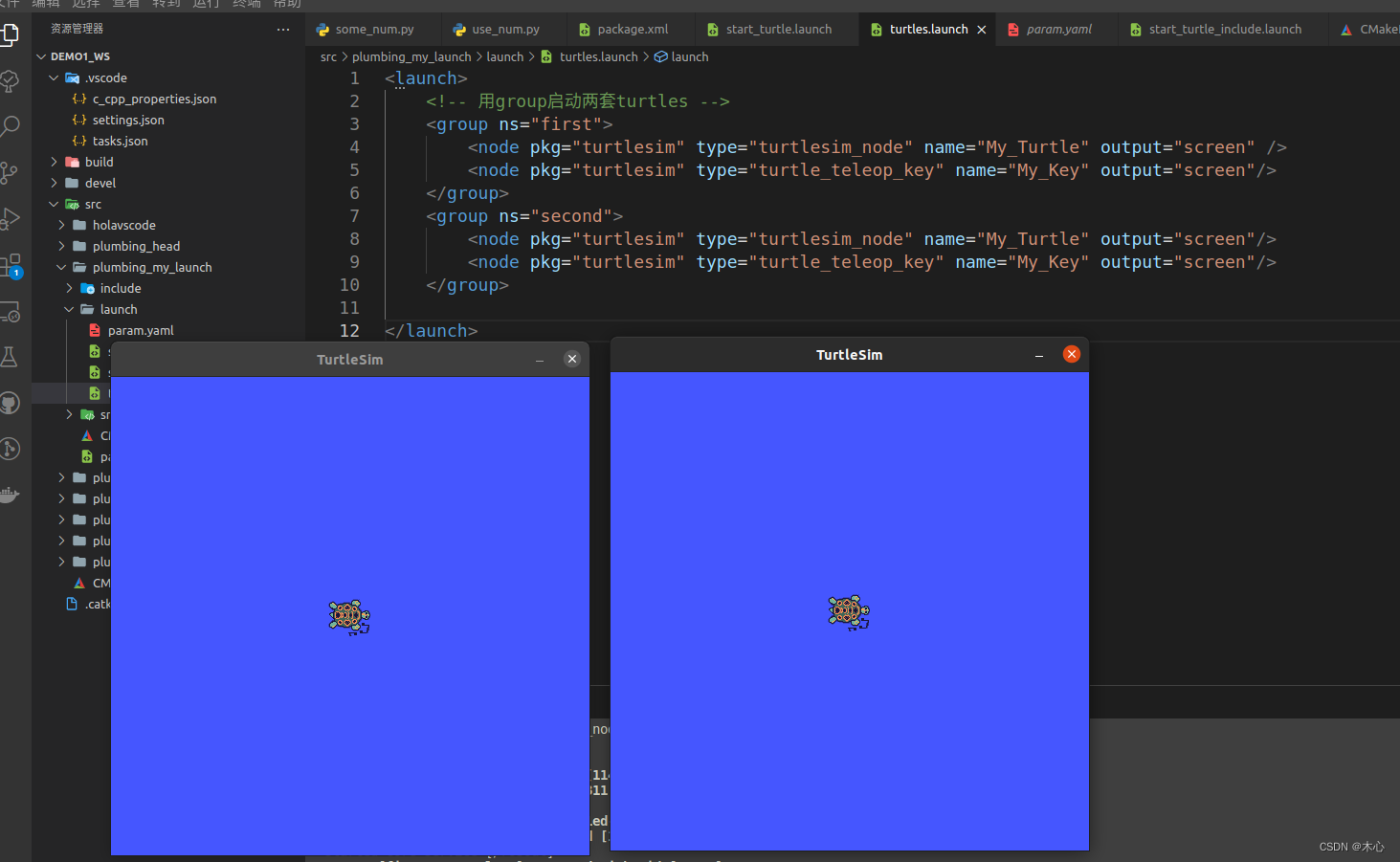
【ROS学习笔记11】ROS元功能包与launch文件的使用
【ROS学习笔记11】ROS元功能包与launch文件的使用 文章目录【ROS学习笔记11】ROS元功能包与launch文件的使用前言一、ROS元功能包二、ROS节点运行管理launch文件2.1 launch文件标签之launch2.2 launch文件标签之node2.3 launch文件标签之include2.4 launch文件标签之remap2.5 l…...

【python】
print函数 同时输出多行变量 print(a, b, sep\n) (23条消息) python3 中print函数参数详解,print(*values, sep , end\n, filesys.stdout, flushFalse)中参数介绍_sep,_phantom-dapeng的博客-CSDN博客 input() 输入浮点数,不能用int(input()) int()…...
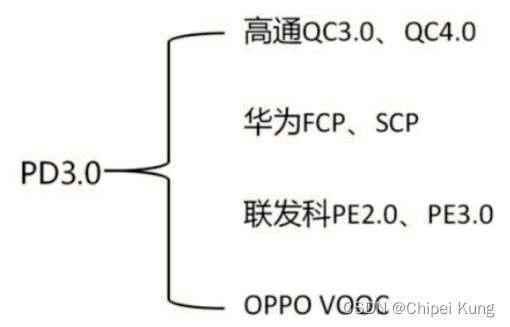
充电协议: 快充协议,如何选充电宝?
快充协议(存在两种:电压; 电流) 目前市面上的快充技术大多遵循2个技术方向: 以高通QC、联发科PEP、华为FCP为首的高压低电流快充技术; 另一种就是以OPPO的VOOC以及华为SCP为首的低电压大电流快充技术。 目前常见的快充标准还有三星AFC、联发…...
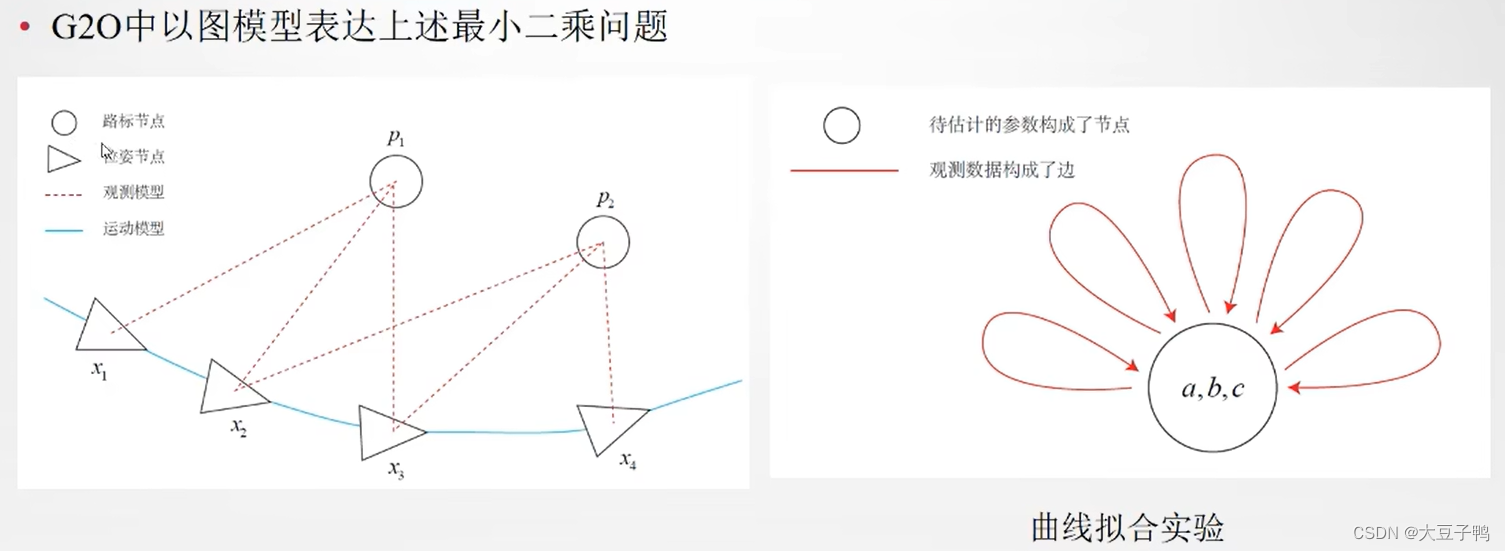
视觉SLAM十四讲ch6 非线性优化笔记
视觉SLAM十四讲ch6 非线性优化笔记本讲目标上讲回顾状态估计问题非线性最小二乘Gauss-Newton:高斯牛顿Levenburg-Marquadt:列文伯格-马夸尔特小结实践:CERES实践:G2O本讲目标 理解最小二乘法的含义和处理方式。 理解Gauss-Newton…...

Nikto工具使用指南
NiktoNikto是一款开源网站服务器扫描器,使用Perl开发,可以对服务器进行全面扫描,包括6400多个潜在危险的文件/cgi(通用网关接口(Common Gateway Interface)),废话不多说,直接上命令:基本测试&am…...
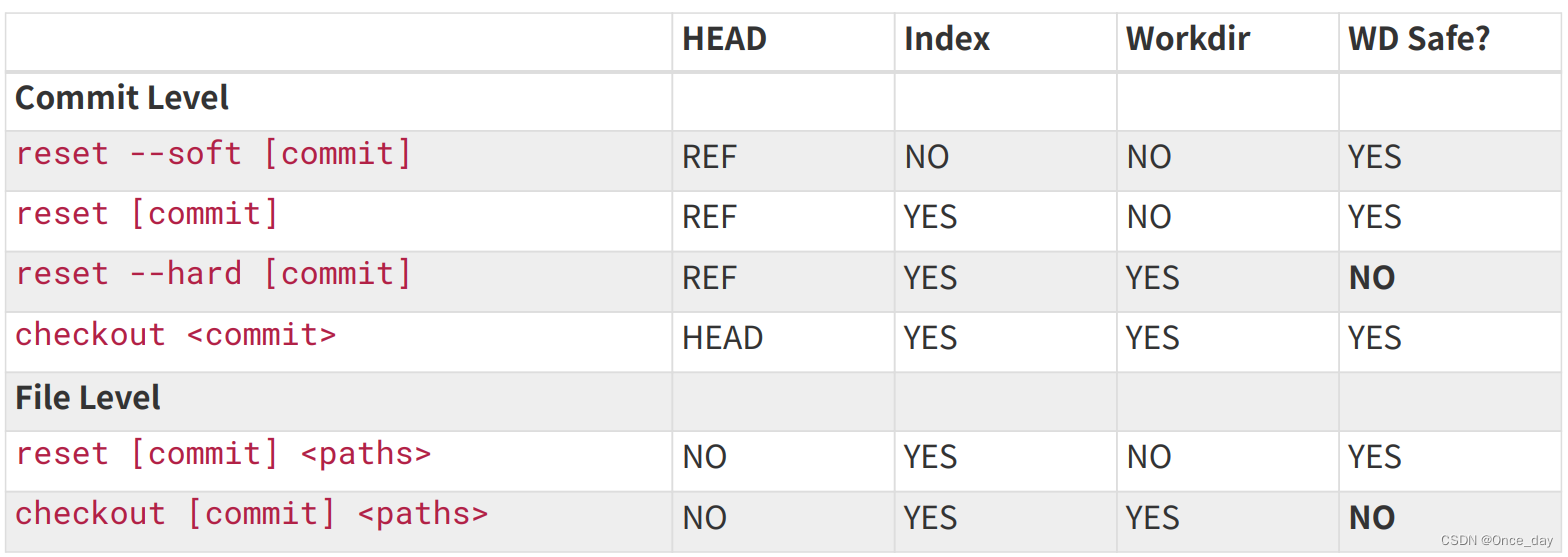
Git(4)之基本工具
Git基础之基本工具 Author:onceday date:2023年3月5日 满满长路有人对你微笑过嘛… windows安装可参考文章:git简易配置_onceday_CSDN博客 參考文档: 《progit2.pdf》,Progit2 Github。《git-book.pdf》 文章目录…...

好书推荐。
个人喜欢看传记,散文,历史等 二战名人传记,苏联列宁,朱可夫,斯大林等 英国首相丘吉尔,美国富兰克林,中国毛泽东等 创业:比尔盖,扎克伯格,苹果公司创始人乔…...

[Pytorch]DataSet和DataLoader逐句详解
将自己的数据集引入Pytorch是搭建属于自己的神经网络的重要一步,这里我设计了一个简单的实验,结合这个实验代码,我将逐句教会大家如何将数据引入DataLoader。 这里以目标检测为例,一个batch中包含图片文件、先验框的框体坐标、目标…...
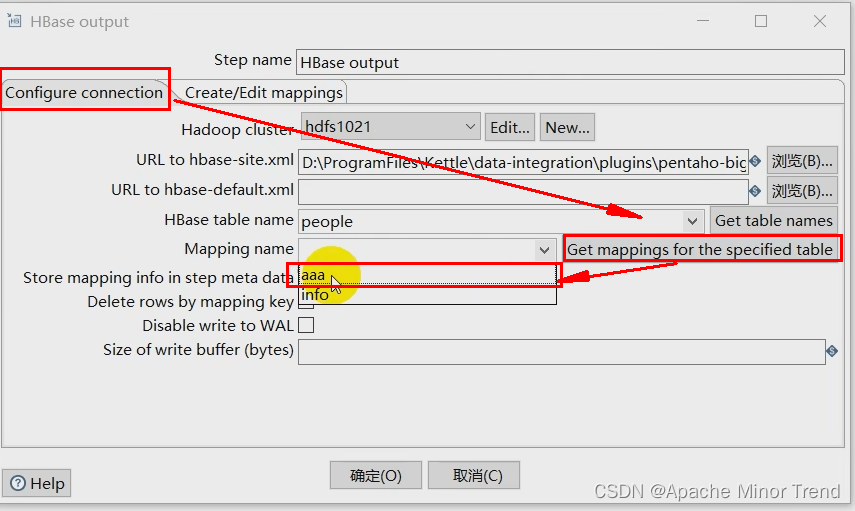
【Kettle-佛系总结】
Kettle-佛系总结Kettle-佛系总结1.kettle介绍2.kettle安装3.kettle目录介绍4.kettle核心概念1.转换2.步骤3.跳(Hop)4.元数据5.数据类型6.并行7.作业5.kettle转换1.输入控件1.csv文件输入2.文本文件输入3.Excel输入4.XML输入5.JSON输入6.表输入2.输出控件…...

JavaSE网络编程
JavaSE网络编程一、基本概念二、常用类三、使用方法1、创建服务器端Socket2、创建客户端Socket3、创建URL对象JavaSE中的网络编程模块提供了一套完整的网络编程接口,可以方便地实现各种基于网络的应用程序。本文将介绍JavaSE中网络编程模块的基本知识、常用类以及使…...

9万字“联、管、用”三位一体雪亮工程整体建设方案
本资料来源公开网络,仅供个人学习,请勿商用。部分资料内容: 1、 总体设计方案 围绕《公共安全视频监控建设联网应用”十三五”规划方案》中的总体架构和一总两分结构要求的基础上,项目将以“加强社会公共安全管理,提高…...

springboot自动装配原理
引言 springboot的自动装配是其重要特性之一,在使用中我们只需在maven中引入需要的starter,然后相应的Bean便会自动注册到容器中。例如: <dependency><groupId>org.springframework.boot</groupId><artifactId>spr…...
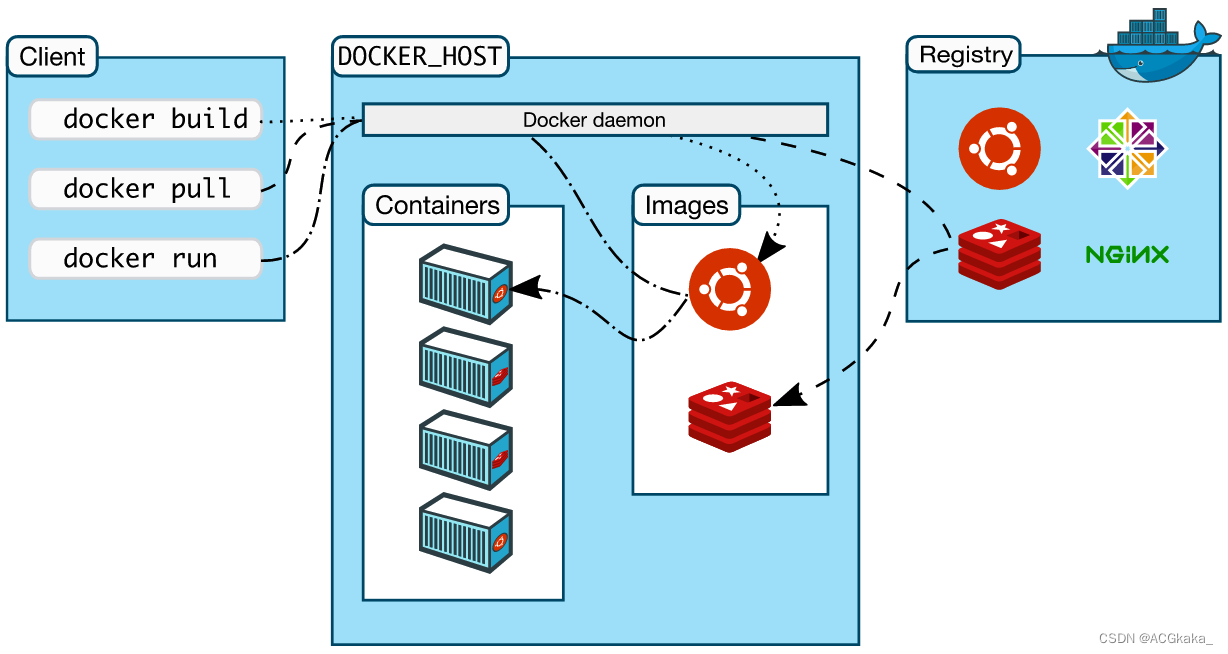
Docker学习(二十)什么是分层存储?
目录1.简介2.什么是 Union Mount?3.分层介绍1)lowerdir 层(镜像层)2)upperdir 层(容器层)3)merged 层4.工作原理1)读:2)写:3ÿ…...
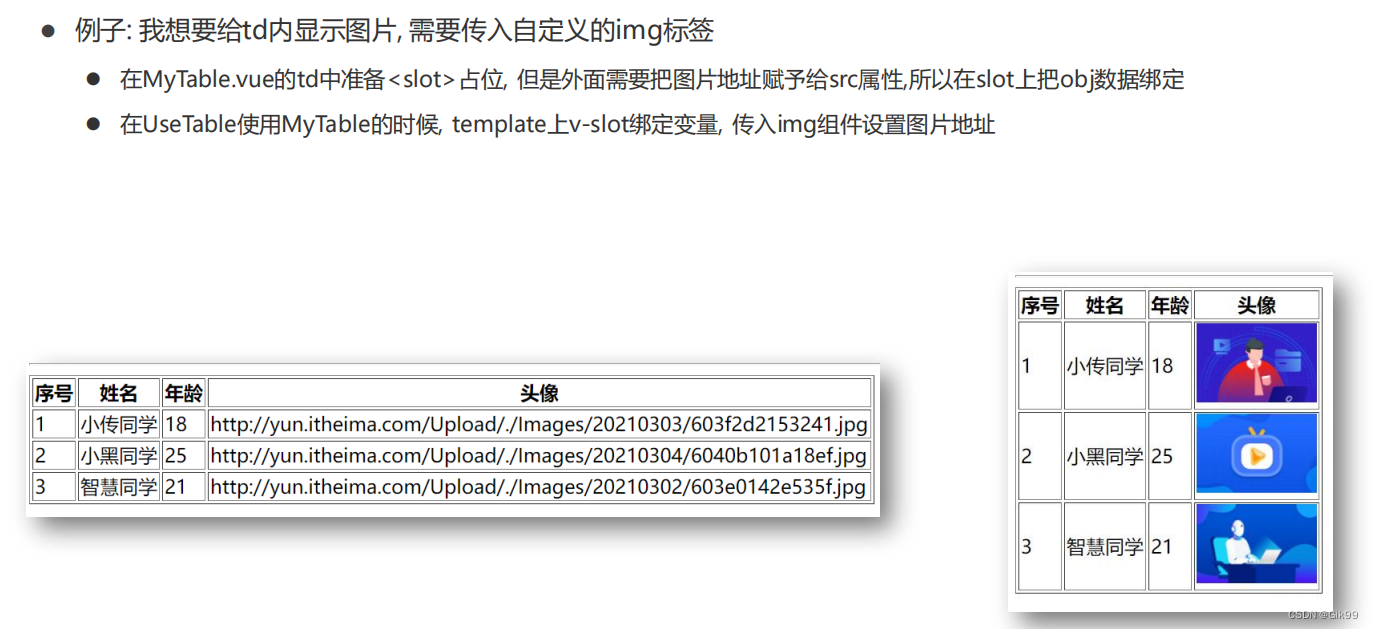
Vue组件进阶(动态组件,组件缓存,组件插槽,具名插槽,作用域插槽)与自定义指令
Vue组件进阶与自定义指令一、Vue组件进阶1.1 动态组件1.2 组件缓存1.3 组件激活和非激活1.4 组件插槽1.5 具名插槽1.6 作用域插槽1.7 作用域插槽使用场景二、自定义指令2.1 自定义指令--注册2.2 自定义指令-传参一、Vue组件进阶 1.1 动态组件 多个组件使用同一个挂载点&#x…...

僵尸进程与孤儿进程
概念 在 Unix/Linux 系统中,正常情况下,子进程是通过父进程创建的,且两者的运行是相互独立的,父进程永远无法预测子进程到底什么时候结束。当一个进程调用 exit 命令结束自己的生命时,其实它并没有真正的被销毁&#…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...
