费解的开关/翻硬币
🌱博客主页:大寄一场.
🌱系列专栏: 算法
😘博客制作不易欢迎各位👍点赞+⭐收藏+➕关注
题目:费解的开关
你玩过“拉灯”游戏吗?
25盏灯排成一个 5×5 的方形。
每一个灯都有一个开关,游戏者可以改变它的状态。
每一步,游戏者可以改变某一个灯的状态。
游戏者改变一个灯的状态会产生连锁反应:和这个灯上下左右相邻的灯也要相应地改变其状态。
我们用数字 1 表示一盏开着的灯,用数字 0 表示关着的灯。
下面这种状态
10111
01101
10111
10000
11011在改变了最左上角的灯的状态后将变成:
01111
11101
10111
10000
11011再改变它正中间的灯后状态将变成:
01111
11001
11001
10100
11011给定一些游戏的初始状态,编写程序判断游戏者是否可能在 6 步以内使所有的灯都变亮。
输入格式
第一行输入正整数 n,代表数据中共有 n 个待解决的游戏初始状态。
以下若干行数据分为 n 组,每组数据有 5 行,每行 5个字符。
每组数据描述了一个游戏的初始状态。
各组数据间用一个空行分隔。
输出格式
一共输出 n 行数据,每行有一个小于等于 6的整数,它表示对于输入数据中对应的游戏状态最少需要几步才能使所有灯变亮。
对于某一个游戏初始状态,若 6步以内无法使所有灯变亮,则输出 −1。
数据范围
0<n≤500
输入样例:
3
00111
01011
10001
11010
1110011101
11101
11110
11111
1111101111
11111
11111
11111
11111输出样例:
3
2
-1
例如:
00111
01011
10001
11010
11100
则最少需要3步
算法思路:
我们枚举第一行的点击方法(按或不按),共2^5=32种,完成第一行的点击后,固定第一行,
从第一行开始递推,若最后一行有0(暗),说明这种方式无解。在所有合法的点击方式中取点击次数最少的就是答案。若点击次数大于6还无法使所有灯变亮,则输出 −1。
时间复杂度:32*25*5*500 = 200 000 000
对第一行操作有32种可能 * 25个格子 * 每一次操作都要改变5个灯的状态 * 最多读入的时候可能有500次light矩阵
最关键的两点
1.要使得步数最少则每一个位置最多只会被点击一次
2.每一行开关的操作被前一行灯的亮灭所操作。

比如说 上图若固定第一行,则第二行只能操作第二格。
所以说第一行的固定可以决定整个棋盘的操作。
那么我们如何枚举第一行的操作呢?
若用0 (不操作)1(操作)来表示
举个栗子 :
1 1 1 1 1->用10进制表示为31
0 0 0 0 0->用10进制表示为0
即第一行的操作可以用 0~2^5 -1=31来对应
tips:这里如何判断op的二进制表示的第k位是否为1
op>>k&1
再举个栗子 26->1 1 0 1 0 (位数分别为 4 3 2 1 0) 判断它的第一位是否为1
1 1 0 1 0>>1 ->1 1 0 1
1 1 0 1&1=1(&运算 两个位都为1时,结果为1。)
for (int op = 0; op < 32; op ++ )//枚举第一行的操作{int step = 0;for (int i = 0; i < 5; i ++ )if (op >> i & 1){step ++ ;turn(0, i);}}操作五个灯(偏移量)
turn(x,y)
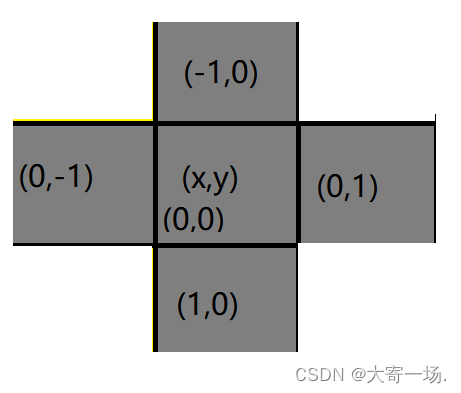
int dx[5] = {-1, 0, 1, 0, 0}, dy[5] = {0, 1, 0, -1, 0};//偏移量
void turn(int x, int y)
{for (int i = 0; i < 5; i ++ ){int a = x + dx[i], b = y + dy[i];if (a < 0 || a >= 5 || b < 0 || b >= 5)//判断是否出界continue; g[a][b] ^= 1;//‘0’的ascall码为48;二进制表示110000,‘1’的ascall码为49;二进制表示110001}
}判断最后一行灯的情况
bool dark = false;//判断最后一行是否有暗,有则方案无解for (int i = 0; i < 5; i ++ )if (g[4][i] == '0'){dark = true;break;}if (!dark) res = min(res, step);//无则记录最小步数完整代码:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 6;// /‘0’
char g[N][N], backup[N][N];
int dx[5] = {-1, 0, 1, 0, 0}, dy[5] = {0, 1, 0, -1, 0};//偏移量void turn(int x, int y)
{for (int i = 0; i < 5; i ++ ){int a = x + dx[i], b = y + dy[i];if (a < 0 || a >= 5 || b < 0 || b >= 5)//判断是否出界continue; g[a][b] ^= 1;//‘0’的ascall码为48;二进制表示110000,‘1’的ascall码为49;二进制表示110001}
}int main()
{int T;cin >> T;while (T -- )//T组测试数据{for (int i = 0; i < 5; i ++) //打印棋盘5*5cin >> g[i];int res = 10;for (int op = 0; op < 32; op ++ )//枚举第一行的操作{memcpy(backup, g, sizeof g);int step = 0;for (int i = 0; i < 5; i ++ )if (op >> i & 1){step ++ ;turn(0, i);}for (int i = 0; i < 4; i ++ )for (int j = 0; j < 5; j ++ )if (g[i][j] == '0'){step ++ ;turn(i + 1, j);}bool dark = false;//判断最后一行是否有暗,有则方案无解for (int i = 0; i < 5; i ++ )if (g[4][i] == '0'){dark = true;break;}if (!dark) res = min(res, step);memcpy(g, backup, sizeof g);}if (res > 6) res = -1;cout << res << endl;}return 0;
}题目:翻硬币
小明正在玩一个“翻硬币”的游戏。
桌上放着排成一排的若干硬币。我们用 * 表示正面,用 o 表示反面(是小写字母,不是零)。
比如,可能情形是:
**oo***oooo如果同时翻转左边的两个硬币,则变为:
oooo***oooo现在小明的问题是:如果已知了初始状态和要达到的目标状态,每次只能同时翻转相邻的两个硬币,那么对特定的局面,最少要翻动多少次呢?
我们约定:把翻动相邻的两个硬币叫做一步操作。
输入格式
两行等长的字符串,分别表示初始状态和要达到的目标状态。
输出格式
一个整数,表示最小操作步数
数据范围
输入字符串的长度均不超过100。
数据保证答案一定有解。输入样例1:
********** o****o****输出样例1:
5输入样例2:
*o**o***o*** *o***o**o***输出样例2:
1
从左开始遍历,一次翻转相邻的俩个
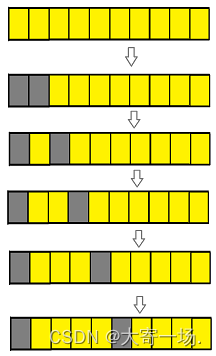
关键的两点
1.操作顺序无影响
2.最多一次
翻转操作
void turn(int i)
{if(start[i]=='*') start[i]='o';else start[i]='*';}完整代码:
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;const int N=110;//输入字符串的长度均不超过100。
int n;
char start[N],ed[N];//两行等长的字符串,分别表示初始状态和要达到的目标状态。void turn(int i)
{if(start[i]=='*') start[i]='o';else start[i]='*';}int main()
{cin>>start>>ed;n=strlen(start);int res=0;for(int i=0;i<n-1;i++)//从左开始遍历if(start[i]!=ed[i]) //判断初始状态和目标状态是否相同{turn(i),turn(i+1); //不同则翻转相邻俩个硬币res++;}cout<<res<<endl;
return 0;
}看到这里的话,感谢各位佬的支持!
相关文章:

费解的开关/翻硬币
🌱博客主页:大寄一场. 🌱系列专栏: 算法 😘博客制作不易欢迎各位👍点赞⭐收藏➕关注 题目:费解的开关 你玩过“拉灯”游戏吗? 25盏灯排成一个 55 的方形。 每一个灯都有一个开关&…...
OpenGL中的坐标系
1、2D笛卡尔坐标系2D笛卡尔坐标系跟我们高中的时候学习的坐标系一样,是由x、y决定的。2、3D笛卡尔坐标系3D笛卡尔坐标系坐标由x、y、z决定,满足右手定则。3、视口glViewport(GLint x,GLint y,GLsizei width,GLsizei height)窗口和视口大小可以相同&#…...

Spring——Spring介绍和IOC相关概念
Spring是以Spring Framework为核心,其余的例如Spring MVC, Spring Cloud,Spring Data,Spring Security SpringBoot的基础都是Spring Framework。 Spring Boot可以在简化开发的基础上加速开发。 Spring Cloud分布式开发 Spring有…...

A+B Problem
AB Problem 题目描述 输入两个整数 a,ba, ba,b,输出它们的和(∣a∣,∣b∣≤109|a|,|b| \le {10}^9∣a∣,∣b∣≤109)。 注意 Pascal 使用 integer 会爆掉哦!有负数哦!C/C 的 main 函数必须是 int 类型,…...
【ROS学习笔记11】ROS元功能包与launch文件的使用
【ROS学习笔记11】ROS元功能包与launch文件的使用 文章目录【ROS学习笔记11】ROS元功能包与launch文件的使用前言一、ROS元功能包二、ROS节点运行管理launch文件2.1 launch文件标签之launch2.2 launch文件标签之node2.3 launch文件标签之include2.4 launch文件标签之remap2.5 l…...

【python】
print函数 同时输出多行变量 print(a, b, sep\n) (23条消息) python3 中print函数参数详解,print(*values, sep , end\n, filesys.stdout, flushFalse)中参数介绍_sep,_phantom-dapeng的博客-CSDN博客 input() 输入浮点数,不能用int(input()) int()…...
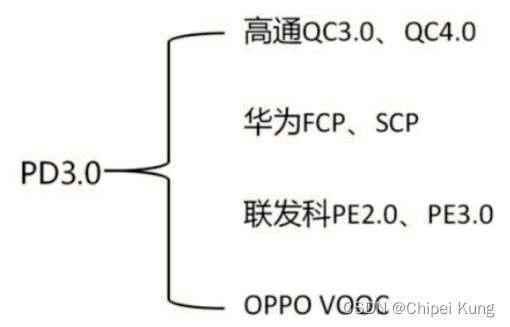
充电协议: 快充协议,如何选充电宝?
快充协议(存在两种:电压; 电流) 目前市面上的快充技术大多遵循2个技术方向: 以高通QC、联发科PEP、华为FCP为首的高压低电流快充技术; 另一种就是以OPPO的VOOC以及华为SCP为首的低电压大电流快充技术。 目前常见的快充标准还有三星AFC、联发…...
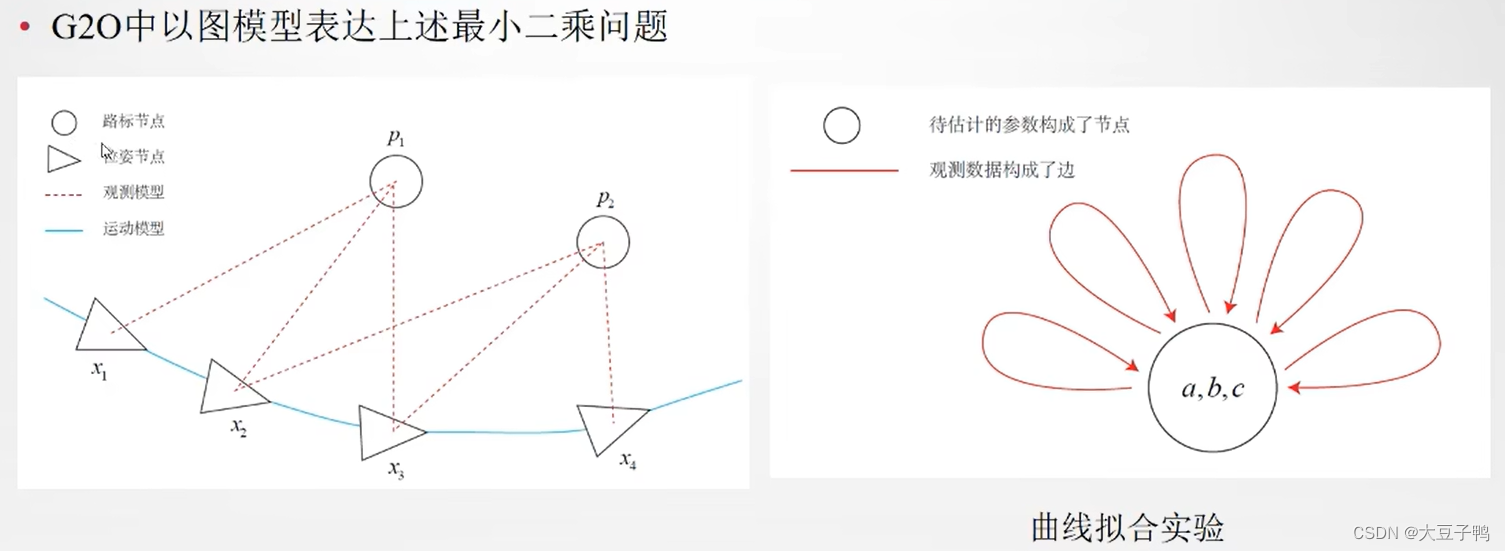
视觉SLAM十四讲ch6 非线性优化笔记
视觉SLAM十四讲ch6 非线性优化笔记本讲目标上讲回顾状态估计问题非线性最小二乘Gauss-Newton:高斯牛顿Levenburg-Marquadt:列文伯格-马夸尔特小结实践:CERES实践:G2O本讲目标 理解最小二乘法的含义和处理方式。 理解Gauss-Newton…...

Nikto工具使用指南
NiktoNikto是一款开源网站服务器扫描器,使用Perl开发,可以对服务器进行全面扫描,包括6400多个潜在危险的文件/cgi(通用网关接口(Common Gateway Interface)),废话不多说,直接上命令:基本测试&am…...
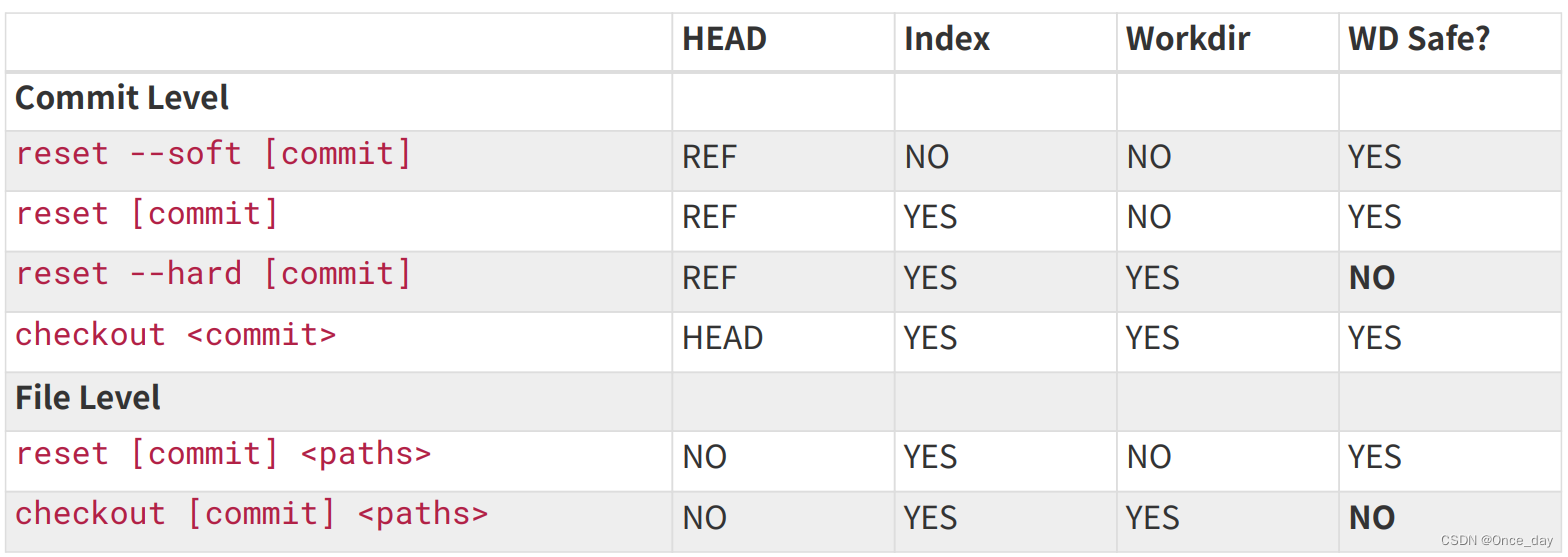
Git(4)之基本工具
Git基础之基本工具 Author:onceday date:2023年3月5日 满满长路有人对你微笑过嘛… windows安装可参考文章:git简易配置_onceday_CSDN博客 參考文档: 《progit2.pdf》,Progit2 Github。《git-book.pdf》 文章目录…...

好书推荐。
个人喜欢看传记,散文,历史等 二战名人传记,苏联列宁,朱可夫,斯大林等 英国首相丘吉尔,美国富兰克林,中国毛泽东等 创业:比尔盖,扎克伯格,苹果公司创始人乔…...

[Pytorch]DataSet和DataLoader逐句详解
将自己的数据集引入Pytorch是搭建属于自己的神经网络的重要一步,这里我设计了一个简单的实验,结合这个实验代码,我将逐句教会大家如何将数据引入DataLoader。 这里以目标检测为例,一个batch中包含图片文件、先验框的框体坐标、目标…...
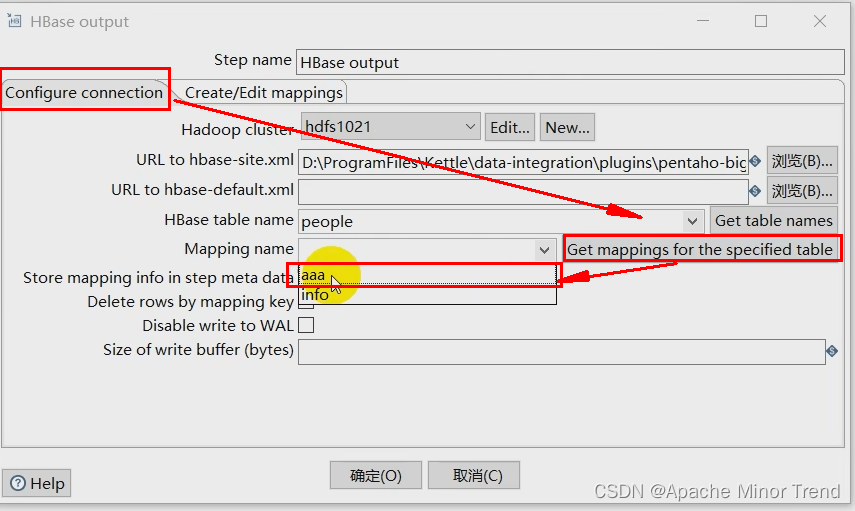
【Kettle-佛系总结】
Kettle-佛系总结Kettle-佛系总结1.kettle介绍2.kettle安装3.kettle目录介绍4.kettle核心概念1.转换2.步骤3.跳(Hop)4.元数据5.数据类型6.并行7.作业5.kettle转换1.输入控件1.csv文件输入2.文本文件输入3.Excel输入4.XML输入5.JSON输入6.表输入2.输出控件…...

JavaSE网络编程
JavaSE网络编程一、基本概念二、常用类三、使用方法1、创建服务器端Socket2、创建客户端Socket3、创建URL对象JavaSE中的网络编程模块提供了一套完整的网络编程接口,可以方便地实现各种基于网络的应用程序。本文将介绍JavaSE中网络编程模块的基本知识、常用类以及使…...

9万字“联、管、用”三位一体雪亮工程整体建设方案
本资料来源公开网络,仅供个人学习,请勿商用。部分资料内容: 1、 总体设计方案 围绕《公共安全视频监控建设联网应用”十三五”规划方案》中的总体架构和一总两分结构要求的基础上,项目将以“加强社会公共安全管理,提高…...

springboot自动装配原理
引言 springboot的自动装配是其重要特性之一,在使用中我们只需在maven中引入需要的starter,然后相应的Bean便会自动注册到容器中。例如: <dependency><groupId>org.springframework.boot</groupId><artifactId>spr…...
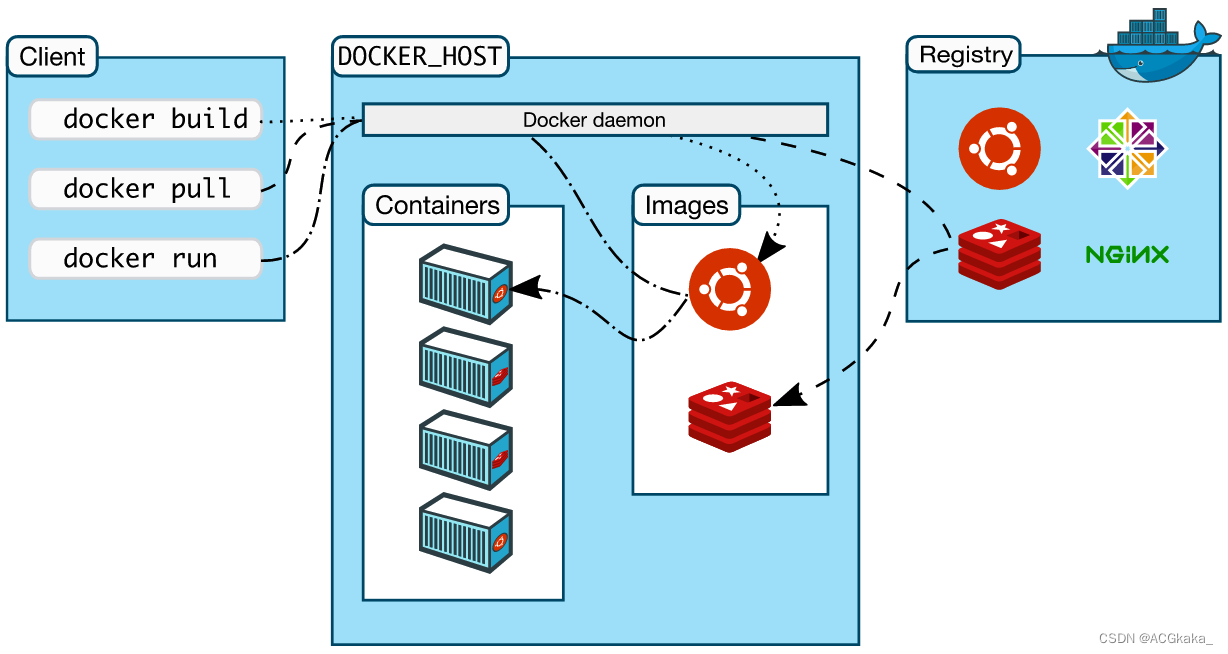
Docker学习(二十)什么是分层存储?
目录1.简介2.什么是 Union Mount?3.分层介绍1)lowerdir 层(镜像层)2)upperdir 层(容器层)3)merged 层4.工作原理1)读:2)写:3ÿ…...
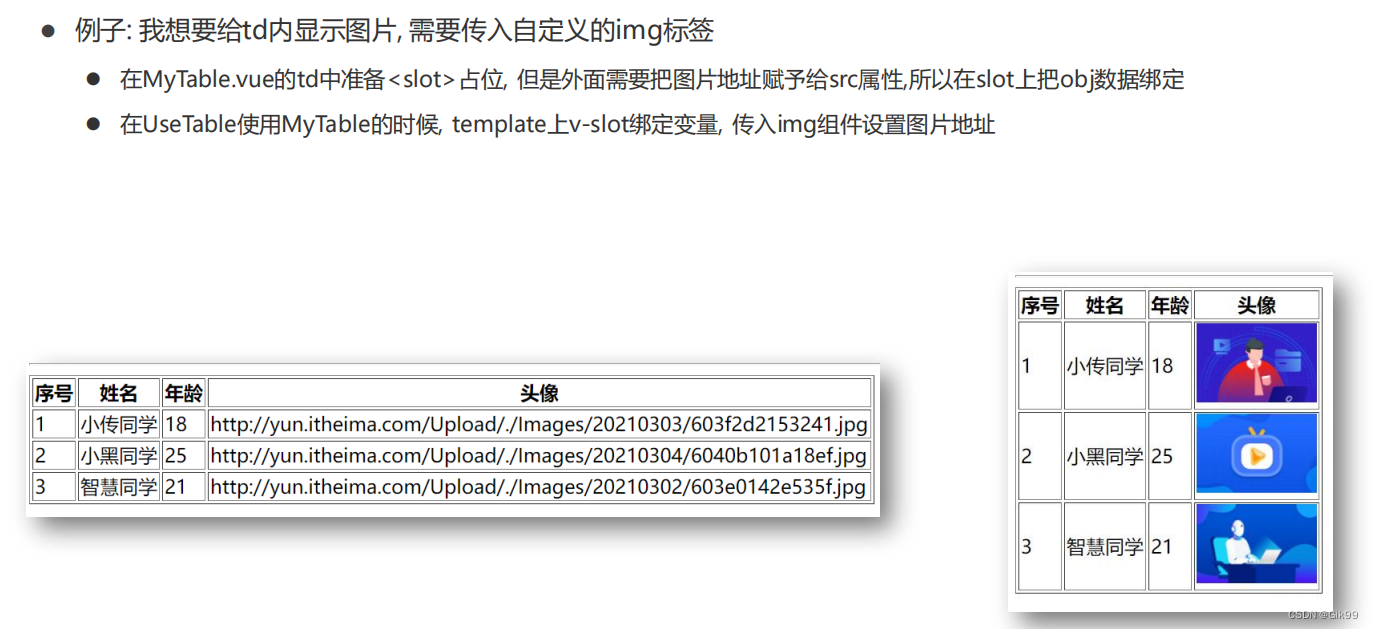
Vue组件进阶(动态组件,组件缓存,组件插槽,具名插槽,作用域插槽)与自定义指令
Vue组件进阶与自定义指令一、Vue组件进阶1.1 动态组件1.2 组件缓存1.3 组件激活和非激活1.4 组件插槽1.5 具名插槽1.6 作用域插槽1.7 作用域插槽使用场景二、自定义指令2.1 自定义指令--注册2.2 自定义指令-传参一、Vue组件进阶 1.1 动态组件 多个组件使用同一个挂载点&#x…...

僵尸进程与孤儿进程
概念 在 Unix/Linux 系统中,正常情况下,子进程是通过父进程创建的,且两者的运行是相互独立的,父进程永远无法预测子进程到底什么时候结束。当一个进程调用 exit 命令结束自己的生命时,其实它并没有真正的被销毁&#…...
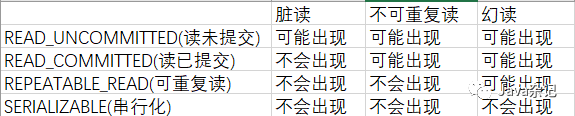
基于注解@Transactional事务基本用法
关于概念性的放在最下面,熟读几遍 在使用时候也没多关注,总是加个Transactional 初识下 一般查询 Transactional(propagation Propagation.SUPPORTS) 增删改 Transactional(propagation Propagation.REQUIRED) 当然不能这么马虎 Spring中关于事务的传播 一个个测试,事…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...
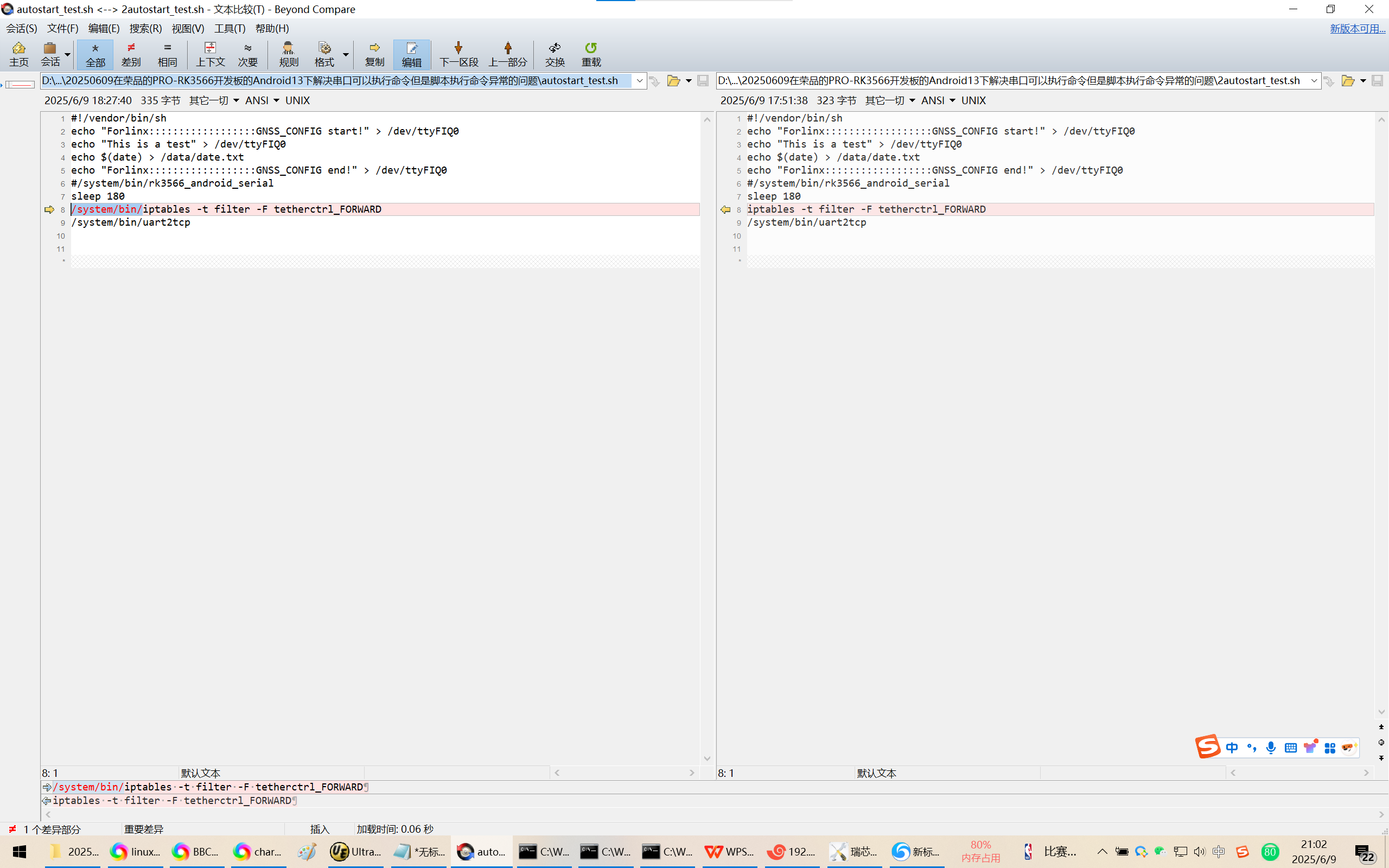
20250609在荣品的PRO-RK3566开发板的Android13下解决串口可以执行命令但是脚本执行命令异常的问题
20250609在荣品的PRO-RK3566开发板的Android13下解决串口可以执行命令但是脚本执行命令异常的问题 2025/6/9 20:54 缘起,为了跨网段推流,千辛万苦配置好了网络参数。 但是命令iptables -t filter -F tetherctrl_FORWARD可以在调试串口/DEBUG口正确执行。…...

Python 解释器安装全攻略(适用于 Linux / Windows / macOS)
目录 一、Windows安装Python解释器1.1 下载并安装Python解释1.2 测试安装是否成功1.3 设置pip的国内镜像------永久配置 二、macOS安装Python解释器三、Linux下安装Python解释器3.1 Rocky8.10/Rocky9.5安装Python解释器3.2 Ubuntu2204/Ubuntu2404安装Python解释器3.3 设置pip的…...

Async-profiler 内存采样机制解析:从原理到实现
引言 在 Java 性能调优的工具箱中,async-profiler 是一款备受青睐的低开销采样分析器。它不仅能分析 CPU 热点,还能精确追踪内存分配情况。本文将深入探讨 async-profiler 实现内存采样的多种机制,结合代码示例解析其工作原理。 为什么需要内…...


