图论基础(一)
一、图论
图论是数学的一个分支,它以图为研究对象。图论中的图是若干给定的点(顶点)以及连接两点的线(边)构成的图像,这种图形通常用来描述某些事物之间的某种特定关系,用点代表事物,用连接两点的线表示相应两个事物间具有这种关系。
图几乎可以用来表现所有类型的结构或系统,从交通网络到通信网络,从下棋游戏到最优流程,从任务分配到人际交互网络,图都有广阔的用武之地。
表示出最基础的图:(这些与点的大小,边的粗细都无关,只表示点与点之间通过边的关系)

二、图的基础

1.顶点(vertex)
在图的应用中,每个顶点代表的含义均不相同,而是相互通过边相联系,因此将图中的每个顶点进行标号进行区分。
①.度数(degree)
与该顶点相关联的总变数,一个图G的总度数 d(V) 等于总边数的两倍,当图的边有方向时(有向图),一个顶点的度可分为出度(out-degree)和入度(in-degree),出度是以该顶点为起点的边数,入度则是以该顶点为终点的边数。
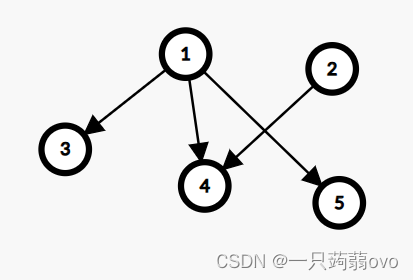
②阶数(order)
图中含有顶点的个数,即含有 n 个顶点,为 n 阶图
2. 边(edge)
顶点与顶点之间通过边联系,构成一个完整的图。
①权重(weight)
边的权重(权值),即每条边都有与之对应的值。
例如将两个顶点看成两个地点,边看成两个地点之间的距离。
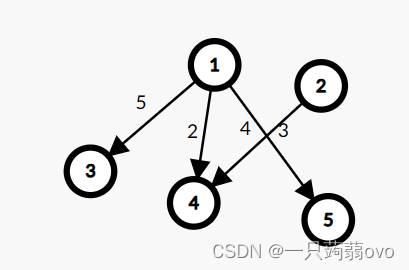
三、图的分类
综合以上,图可以分为以下几种
1.有向图/无向图
最基本的图通常被定义为“无向图”,与之对应的则被称为“有向图”。两者唯一的区别在于,有向图中的边是有方向性的。
无向边:无固定方向的边,既可 x 到 y,又可以 y 到 x
有向边:固定方向的边,即只能 x 到 y ,不能 y 到 x
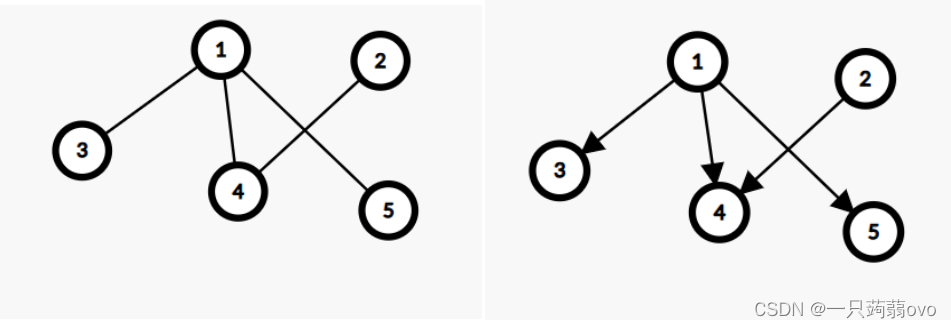
2.有权图/无权图
有权图: 权值就是一条边的长度或代价。
无权图: 不是边的权值为0,而是全都为1。
3.特殊的图——环
在图论中,环是一条只有第一个和最后一个顶点重复的非空路径。一个没有环的图被称作无环图,一个没有有向环的有向图被称做有向无环图。一个无环的连通图被称作树。
4.连通图/连通分量
在图G中,任意两个顶点之间都存在路径,则称G为连通图
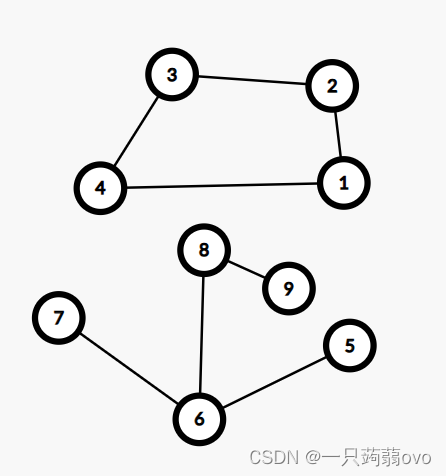
上图虽然不是一个连通图(例 点8 与 点4 不连通),但它有两个连通子图,1234,56789,
把一个图的最大连通子图称为它的连通分量。5,6,7,8,9顶点构成的子图就是该图的最大连通子图,也就是连通分量。
连通分量特点:①子图
②子图是连通的
③子图含有最大的顶点数
对于连通图而言,最大连通分量就是其本身
相关文章:

图论基础(一)
一、图论 图论是数学的一个分支,它以图为研究对象。图论中的图是若干给定的点(顶点)以及连接两点的线(边)构成的图像,这种图形通常用来描述某些事物之间的某种特定关系,用点代表事物,…...

使用 React 和 MUI 创建多选 Checkbox 树组件
在本篇博客中,我们将使用 React 和 MUI(Material-UI)库来创建一个多选 Checkbox 树组件。该组件可以用于展示树形结构的数据,并允许用户选择多个节点。 前提 在开始之前,确保你已经安装了以下依赖: Reac…...

vue3里面使用el-image-vie出现图片预览导致页面卡顿停止加载问题
需求:我们在使用element-plus组件里面的图片预览时候,通过点击按钮来实现图片预览的效果。在开发过程中我们会遇到图片预览的时候出现卡顿出不来,导致当前的页面停止加载了。 具体思路如下: 我们需要添加:preview-teleported“t…...
Leetcoder Day26| 回溯part06:总结+三道hard题
332.重新安排行程 给定一个机票的字符串二维数组 [from, to],子数组中的两个成员分别表示飞机出发和降落的机场地点,对该行程进行重新规划排序。所有这些机票都属于一个从 JFK(肯尼迪国际机场)出发的先生,所以该行程必…...
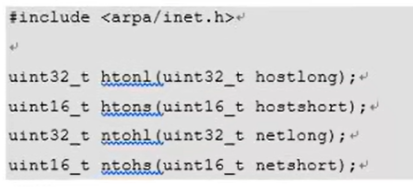
浅谈 Linux 网络编程 - 网络字节序
文章目录 前言核心知识关于 小端法关于 大端法网络字节序的转换 函数 前言 在进行 socket 网络编程时,会用到字节流的转换函数、例如 inet_pton、htons 等,那么为什么要用到这些函数呢,本篇主要就是对这部分进行介绍。 核心知识 重点需要记…...
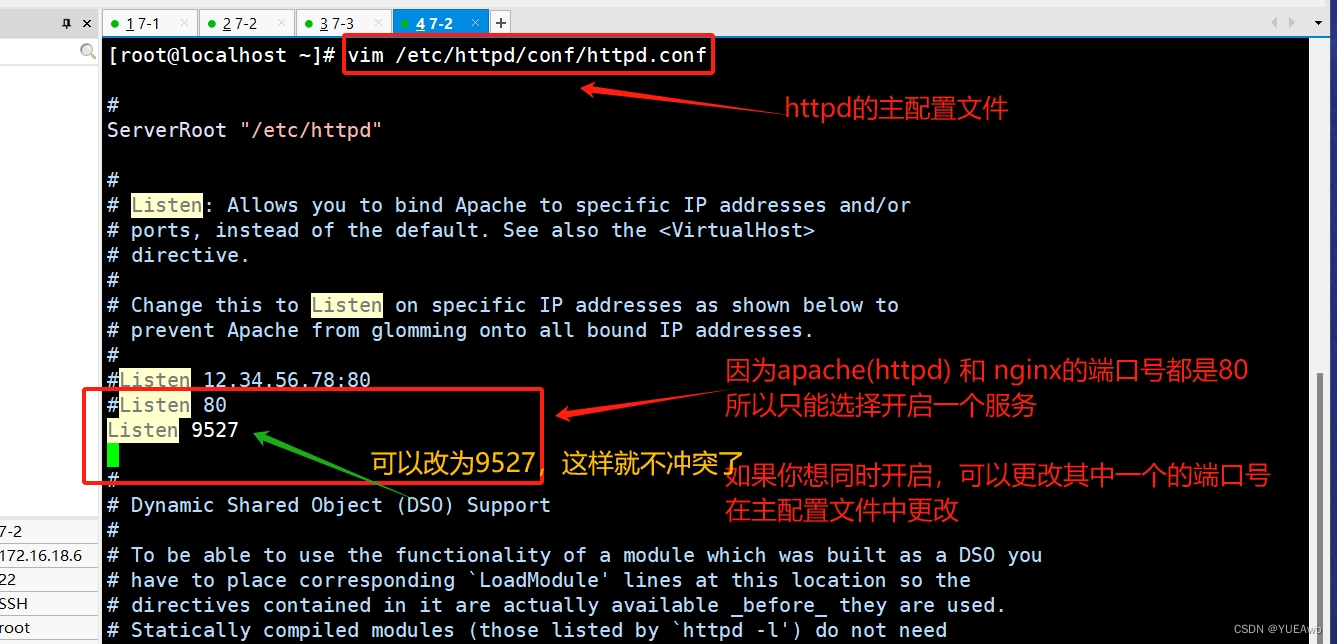
Nginx网络服务六-----IP透传、调度算法和负载均衡
1.实现反向代理客户端 IP 透传 就是在日志里面加上一个变量 Module ngx_http_proxy_module [rootcentos8 ~]# cat /apps/nginx/conf/conf.d/pc.conf server { listen 80; server_name www.kgc.org; location / { index index.html index.php; root /data/nginx/html/p…...
【Linux进程】进程状态---进程僵尸与孤儿
📙 作者简介 :RO-BERRY 📗 学习方向:致力于C、C、数据结构、TCP/IP、数据库等等一系列知识 📒 日后方向 : 偏向于CPP开发以及大数据方向,欢迎各位关注,谢谢各位的支持 目录 1.进程排队2.进程状态…...
一)
MySQL数据库基础知识总结(适合小白入门使用)一
文章目录 一 数据库数据表的创建等基本操作二 数据类型的测试三 完整性约束条件四 数据表结构的相关操作五 对表中数据的操作六 表达式与查询七 高级的查询功能 一 数据库数据表的创建等基本操作 #注释内容(与python很像) -- 也为注释内容 -- 创建一个数…...

历史新知网:寄快递寄个电脑显示器要多少钱?
以下文字信息由(新史知识网)编辑整理发布。 让我们赶紧来看看吧! 问题1:快递寄电脑显示器要多少钱? 此物有多重? 顺丰寄就可以了,但是必须是原包装的,不然不好寄。 问题2࿱…...

在两台CentOS 7服务器上部署MinIO集群。
环境说明: 2台Centos7服务器 IP地址分别为172.16.1.9和172.16.1.10 1. 创建minio用户和目录 在两台服务器上执行以下命令: sudo useradd -m -d /app/minio minio sudo mkdir -p /app/minioData sudo mkdir -p /app/minio/logs sudo chown -R mini…...

【计算机网络】深度学习使用应用层的HTTP协议
💓 博客主页:从零开始的-CodeNinja之路 ⏩ 收录文章:【计算机网络】深度学习使用应用层的HTTP协议 🎉欢迎大家点赞👍评论📝收藏⭐文章 文章目录 一:HTTP是什么二:HTTP请求1.HTTP请求的组成2.HTTP请求的方法…...
Ubuntu18.04 系统上配置并运行SuperGluePretrainedNetwork(仅使用CPU)
SuperGlue是Magic Leap在CVPR 2020上展示的研究项目,它是一个图神经网络(Graph Neural Network)和最优匹配层(Optimal Matching layer)的结合,训练用于对两组稀疏图像特征进行匹配。这个项目提供了PyTorch代…...
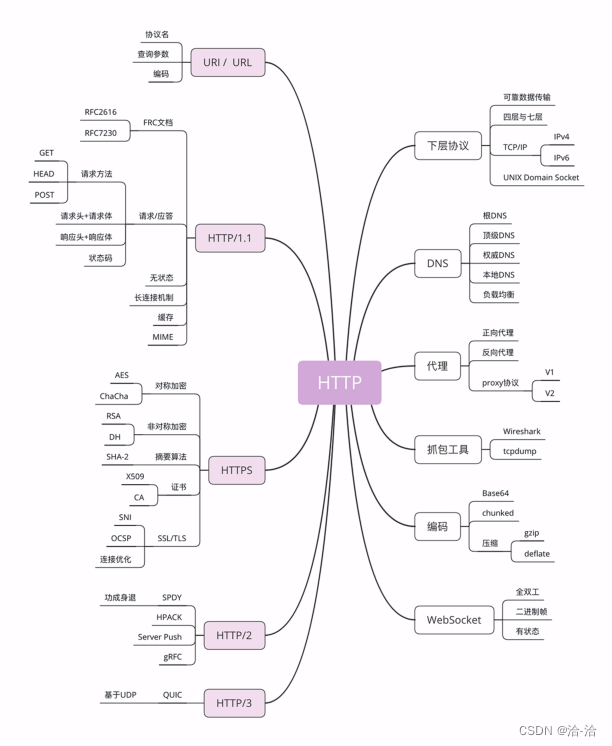
协议-http协议-基础概念01-发展历程-http组成-http是什么-相关的应用-相关的协议
发展历程-http组成-http是什么-相关的应用-相关的协议 参考来源: 极客时间-透视HTTP协议(作者:罗剑锋); 01-HTTP的发展历程 1989 年,任职于欧洲核子研究中心(CERN)的蒂姆伯纳斯 - 李(Tim Ber…...

UI学习-学习内容
教程网址1:UI 新手如何从设计规范中提升自己 推荐一下高质量的设计规范 满屏干货 语雀 B站地址1:新像素 UI 新手如何从设计规范中提升自己 推荐一下高质量的设计规范 满屏干货 UI设计培训_哔哩哔哩_bilibili 教程地址2:UI 新手成长经验分享…...

Flink CDC 提取记录变更时间作为事件时间和 Hudi 表的 precombine.field 以及1970-01-01 取值问题
博主历时三年精心创作的《大数据平台架构与原型实现:数据中台建设实战》一书现已由知名IT图书品牌电子工业出版社博文视点出版发行,点击《重磅推荐:建大数据平台太难了!给我发个工程原型吧!》了解图书详情,…...

【网络安全】网络安全意识教育实用指南
随着科技的不断发展和数字世界的变革,我们不仅从中获得前所未有的力量,也同时面临着前所未有的风险挑战。多数CISO(首席信息安全官)时刻致力于协助企业抵御各种安全威胁。在“武器库”中有一件珍贵的法宝:网络安全意识…...

wordpress模板购买网站推荐
简站wordpress主题 老牌wordpress开发团队,开发过数百款wordpress主题,作品是最好的简历,靠作品说话,看作品喜欢不喜欢就可以了。 https://www.jianzhanpress.com WP模板牛 免费wordpress下载网站,上面有上百款免费…...

LeetCode 刷题 [C++] 第240题.搜索二维矩阵 II
题目描述 编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性: 每行的元素从左到右升序排列。 每列的元素从上到下升序排列。 题目分析 通过分析矩阵的特点发现,其左下角和右上角可以看作一个“二叉搜索树的根节…...
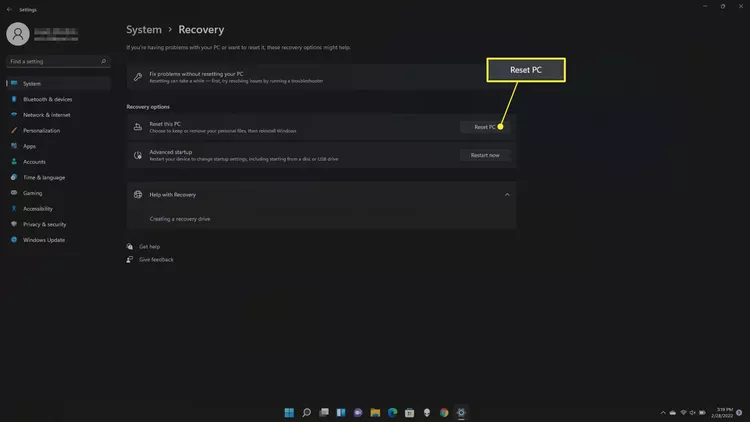
HP笔记本电脑如何恢复出厂设置?这里提供几种方法
要恢复出厂设置Windows 11或10的HP笔记本电脑,你可以使用操作系统的标准方法。如果你运行的是早期版本,你可以使用HP提供的单独程序清除计算机并重新安装操作系统。 恢复出厂设置运行Windows 11的HP笔记本电脑 所有Windows 11计算机都有一个名为“重置此电脑”的功能,可…...
Elasticsearch:了解人工智能搜索算法
作者:来自 Elastic Jessica Taylor, Aditya Tripathi 人工智能工具无处不在,其原因并不神秘。 他们可以执行各种各样的任务并找到许多日常问题的解决方案。 但这些应用程序的好坏取决于它们的人工智能搜索算法。 简单来说,人工智能搜索算法是…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...
