动态规划之买卖股票问题
🌈🌈😄😄
欢迎来到茶色岛独家岛屿,本期将为大家揭晓动态规划之买卖股票问题 ,做好准备了么,那么开始吧。
🌲🌲🐴🐴
- 动态规划算法本质上就是穷举「状态」,然后在「选择」中选择最优解。
- 这个问题的「状态」有三个,第一个是天数,第二个是允许交易的最大次数,第三个是当前的持有状态(即之前说的
rest的状态,我们不妨用 1 表示持有,0 表示没有持有)。然后我们用一个三维数组就可以装下这几种状态的全部组合: - 比如说
dp[3][2][1]的含义就是:今天是第三天,我现在手上持有着股票,至今最多进行 2 次交易。再比如dp[2][3][0]的含义:今天是第二天,我现在手上没有持有股票,至今最多进行 3 次交易。
时刻牢记「状态」的定义,状态
k的定义并不是「已进行的交易次数」,而是「最大交易次数的上限限制」。如果确定今天进行一次交易,且要保证截至今天最大交易次数上限为k,那么昨天的最大交易次数上限必须是k - 1。
状态转移方程:
base case:
dp[-1][...][0] = dp[...][0][0] = 0
dp[-1][...][1] = dp[...][0][1] = -infinity状态转移方程:
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])121. 买卖股票的最佳时机
一、力扣示例
121. 买卖股票的最佳时机 - 力扣(LeetCode) https://leetcode.cn/problems/best-time-to-buy-and-sell-stock/
https://leetcode.cn/problems/best-time-to-buy-and-sell-stock/
二、解决办法
现在发现 k 都是 1,不会改变,即 k 对状态转移已经没有影响了。
可以进行进一步化简去掉所有 k:
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], -prices[i])三、代码实现
class Solution {public int maxProfit(int[] prices) {int n = prices.length;int[][] dp = new int[n][2];for (int i = 0; i < n; i++) {if (i - 1 == -1) {// base casedp[i][0] = 0;dp[i][1] = -prices[i];continue;}dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);dp[i][1] = Math.max(dp[i-1][1], -prices[i]);}return dp[n - 1][0];}
}
122. 买卖股票的最佳时机 II
一、力扣示例
122. 买卖股票的最佳时机 II - 力扣(LeetCode)![]() https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-ii/
https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-ii/
二、解决办法
我们发现数组中的 k 已经不会改变了,也就是说不需要记录 k 这个状态了:
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i])三、代码实现
class Solution {public int maxProfit(int[] prices) {int n=prices.length;int dp[][]=new int[n][2];dp[0][0]=0;dp[0][1]=-prices[0];for(int i=1;i<n;i++){dp[i][0]=Math.max(dp[i-1][0],dp[i-1][1]+prices[i]);dp[i][1]=Math.max(dp[i-1][1],dp[i-1][0]-prices[i]);}return dp[n-1][0];}
}
309. 最佳买卖股票时机含冷冻期
一、力扣示例
309. 最佳买卖股票时机含冷冻期 - 力扣(LeetCode)![]() https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-with-cooldown/
https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-with-cooldown/
二、解决办法
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-2][0] - prices[i])
解释:第 i 天选择 buy 的时候,要从 i-2 的状态转移,而不是 i-1 。三、代码实现
class Solution {public int maxProfit(int[] prices) {int n=prices.length;int dp[][]=new int[n][2];dp[0][0] = 0;dp[0][1] = -prices[0];for(int i=1;i<n;i++){if (i - 2 == -1) {// base case 2dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);dp[i][1] = Math.max(dp[i-1][1], -prices[i]);continue;}dp[i][0]=Math.max(dp[i-1][0],dp[i-1][1]+prices[i]);dp[i][1]=Math.max(dp[i-1][1],dp[i-2][0]-prices[i]);}return dp[n-1][0];}
}
714. 买卖股票的最佳时机含手续费
一、力扣示例
714. 买卖股票的最佳时机含手续费 - 力扣(LeetCode) https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-with-transaction-fee/
https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-with-transaction-fee/
二、解决办法
每次交易要支付手续费,只要把手续费从利润中减去即可,改写方程:dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i] - fee)
解释:相当于买入股票的价格升高了。
在第一个式子里减也是一样的,相当于卖出股票的价格减小了。三、代码实现
class Solution {public int maxProfit(int[] prices, int fee) {int n = prices.length;int[][] dp = new int[n][2];for (int i = 0; i < n; i++) {if (i - 1 == -1) {// base casedp[i][0] = 0;dp[i][1] = -prices[i] - fee;continue;}dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i] - fee);}return dp[n - 1][0];}
}
123. 买卖股票的最佳时机 III
一、力扣示例
123. 买卖股票的最佳时机 III - 力扣(LeetCode)![]() https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iii/
https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iii/
二、解决办法
原始的状态转移方程,没有可化简的地方
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])三、代码实现
class Solution {public int maxProfit(int[] prices) {int max_k = 2, n = prices.length;int[][][] dp = new int[n][max_k + 1][2];for (int i = 0; i < n; i++) {for (int k = 1; k <= max_k; k++) {if (i - 1 == -1) {// 处理 base casedp[i][k][0] = 0;dp[i][k][1] = -prices[i];continue;}dp[i][k][0] = Math.max(dp[i-1][k][0], dp[i-1][k][1] + prices[i]);dp[i][k][1] = Math.max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i]);}}// 穷举了 n × max_k × 2 个状态,正确。return dp[n - 1][max_k][0];}}

188. 买卖股票的最佳时机 IV
一、力扣示例
188. 买卖股票的最佳时机 IV - 力扣(LeetCode)![]() https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iv/
https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iv/
二、解决办法
有了上一题
k = 2的铺垫,这题应该和上一题的第一个解法没啥区别,你把上一题的k = 2换成题目输入的k就行了。但试一下发现会出一个内存超限的错误,原来是传入的
k值会非常大,dp数组太大了。那么现在想想,交易次数k最多有多大呢?一次交易由买入和卖出构成,至少需要两天。所以说有效的限制
k应该不超过n/2,如果超过,就没有约束作用了,相当于k没有限制的情况,而这种情况是之前解决过的。
三、代码实现
class Solution {public int maxProfit(int max_k, int[] prices) {int n = prices.length;if (n <= 0) {return 0;}if (max_k > n / 2) {// 复用之前交易次数 k 没有限制的情况return maxProfit_k_inf(prices);}int[][][] dp = new int[n][max_k + 1][2];// k = 0 时的 base casefor (int i = 0; i < n; i++) {dp[i][0][1] = Integer.MIN_VALUE;dp[i][0][0] = 0;}for (int i = 0; i < n; i++) for (int k = max_k; k >= 1; k--) {if (i - 1 == -1) {// 处理 i = -1 时的 base casedp[i][k][0] = 0;dp[i][k][1] = -prices[i];continue;}dp[i][k][0] = Math.max(dp[i-1][k][0], dp[i-1][k][1] + prices[i]);dp[i][k][1] = Math.max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i]); }return dp[n - 1][max_k][0];}public int maxProfit_k_inf(int[] prices) {int n = prices.length;int[][] dp = new int[n][2];for (int i = 0; i < n; i++) {if (i - 1 == -1) {// base casedp[i][0] = 0;dp[i][1] = -prices[i];continue;}dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] - prices[i]);}return dp[n - 1][0];}
}
相关文章:

动态规划之买卖股票问题
🌈🌈😄😄 欢迎来到茶色岛独家岛屿,本期将为大家揭晓动态规划之买卖股票问题 ,做好准备了么,那么开始吧。 🌲🌲🐴🐴 动态规划算法本质上就是穷举…...

MySQL学习笔记之子查询
自连接方式 自连接就是表A连接表A,通过where关键字实现,比如查询工资比Abel高的员工信息: SELECTe2.last_name,e2.salary FROMemployees e1,employees e2 WHEREe1.last_name "Abel" AND e2.salary > e1.salary;子查询 亦称为…...

HCIP-5OSPF域内域间外部路由学习笔记
1、OSPF区域 每个区域都维护一个独立的LSDB。 Area 0是骨干区域,其他区域都必须与此区域相连。 划分OSPF区域可以缩小路由器的LSDB规模,减少网络流量。 区域内的详细拓扑信息不向其他区域发送,区域间传递的是抽象的路由信息,而不…...

【编程实践】简单是好软件的关键:Simplicity is key to good software
Simplicity is key to good software 简单是好软件的关键 目录 Simplicity is key to good software简单是好软件的关键 Complexity is tempting. 复杂性很诱人。 The smallest way to create value创造价值的最小方法 Simple 简单的 Complexity is tempting. 复杂性很诱人…...
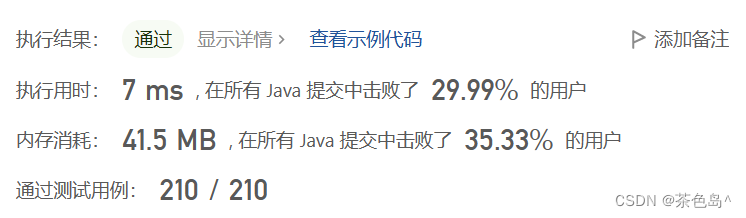
Python|贪心|数组|二分查找|贪心|数学|树|二叉搜索树|在排序数组中查找元素的第一个和最后一个位置|计数质数 |将有序数组转换为二叉搜索树
1、在排序数组中查找元素的第一个和最后一个位置(数组,二分查找) 给定一个按照升序排列的整数数组 nums,和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。 如果数组中不存在目标值 target,返回 […...
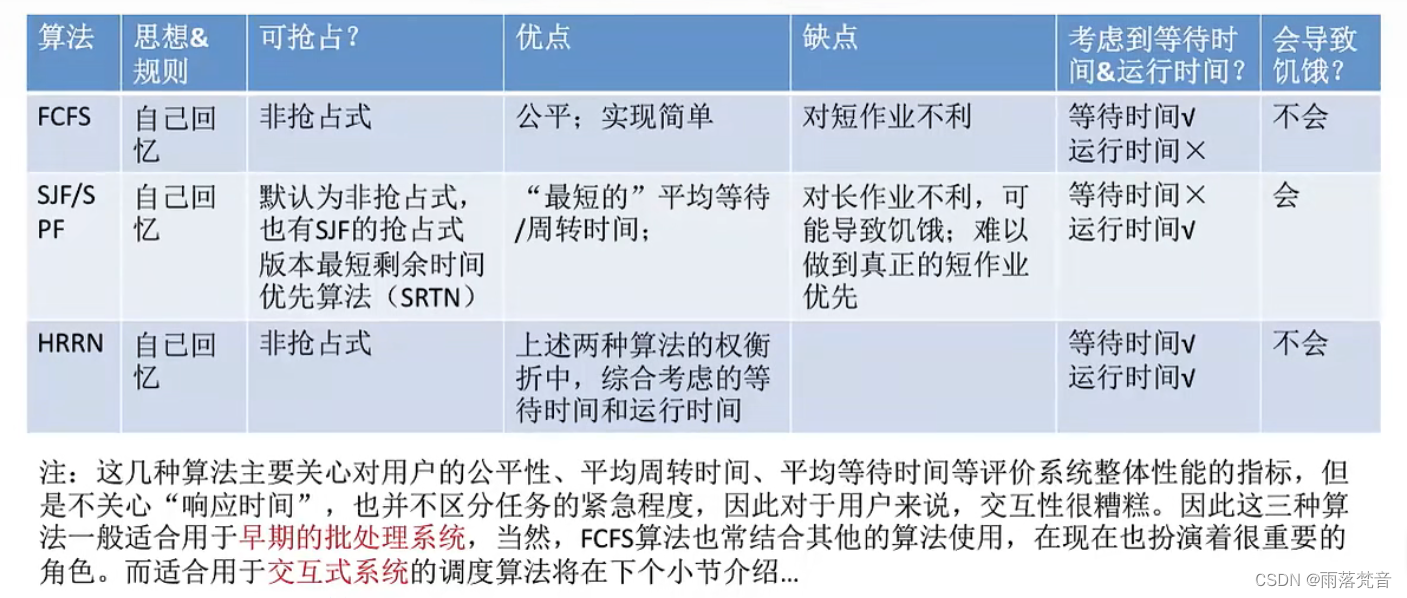
操作系统——15.FCFS、SJF、HRRN调度算法
这节我们来看一下进程调度的FCFS、SJF、HRRN调度算法 目录 1.概述 2.先来先服务算法(FCFS,First Come First Serve) 3.短作业优先算法(SJF,Shortest Job First) 4.高响应比优先算法(HRRN&…...
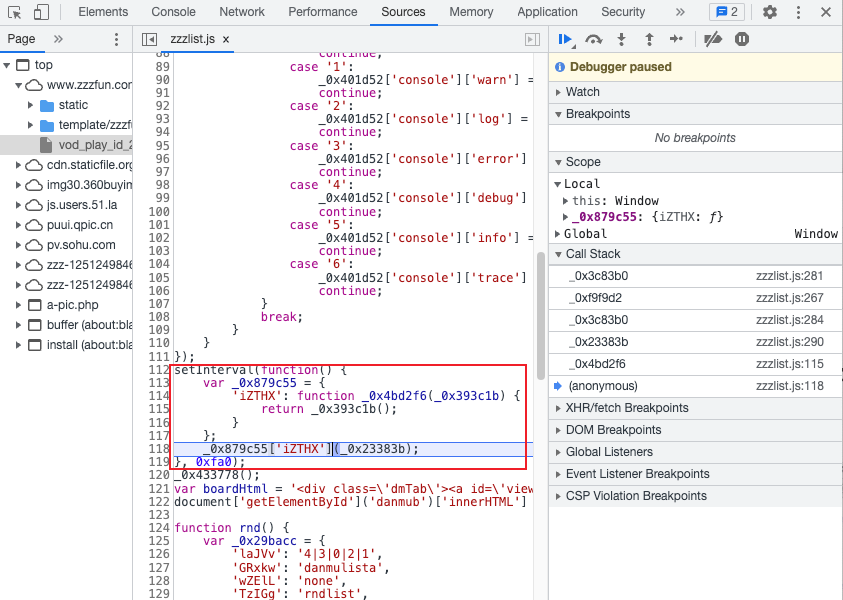
如何防止用户打开浏览器开发者工具?
大家好,我是前端西瓜哥。作为一名前端开发,在浏览一些网页时,有时会在意一些交互效果的实现,会打开开发者工具查看源码实现。 但有些网站做了防窥探处理,打开开发者工具后,会无法再正常进行网页的操作。 …...
C语言-基础了解-12-C数组
C数组 一、C数组 C 语言支持数组数据结构,它可以存储一个固定大小的相同类型元素的顺序集合。数组是用来存储一系列数据,但它往往被认为是一系列相同类型的变量。 数组的声明并不是声明一个个单独的变量,比如 runoob0、runoob1、…、runoo…...

RocksDB 架构
文章目录1、RocksDB 摘要1.1、RocksDB 特点1.2、基本接口1.3、编译2、LSM - Tree2.1、Memtable2.2、WAL2.3、SST2.4、BlockCache3、读写流程3.1、读取流程3.2、写入流程4、LSM-Tree 放大问题4.1、放大问题4.2、compactionRocksDB 是 Facebook 针对高性能磁盘开发开源的嵌入式持…...

MVVM和MVC的区别
首先,MVVM 和 MVC 都是一种设计模式MVCM(Model): 模型层。 用于处理应用程序数据逻辑的部分,模型对象负责在数据库中存取数据V (View): 视图层。 处理数据显示的部分 ,视…...

c++11 标准模板(STL)(std::unordered_map)(三)
定义于头文件 <unordered_map> template< class Key, class T, class Hash std::hash<Key>, class KeyEqual std::equal_to<Key>, class Allocator std::allocator< std::pair<const Key, T> > > class unordered…...
OpenGL环境配置
方法一:1.下载GLFW点击GLFW跳转2.下载后解压3.下载glad,解压后4.用vs2019新建Cmake项目5.在新建的Cmake项目下建立depend文件夹在depend里放置我们下载解压的glad和glfw-3.3.8.bin.WIN646.项目中可以看到我们加进来的文件7.编写我们项目的CMakeLists.txt…...

SpringCloud之 Eureka注册中心
文章目录Eureka注册中心一、服务注册与发现1.1 依赖导入①父工程 SpringCloud 版本管理②Eureka 服务端依赖③Eureka 客户端依赖1.2 服务注册①创建 Eureka 服务端的主类②设置 Eureka 服务端的配置文件③设置 Eureka 客户端的配置文件④关闭自我保护机制1.3 服务发现①远程调用…...

Linux入门篇-用户管理
简介 linux基本的用户管理。 ⽤户的管理(切换到root) ⽤户的添加(useradd) ⽤户的删除(userdel) ⽤户的修改(usermod) ⽤户的查看(查看/etc/passwd) id⽤户组的管理(切换到root) …...
)
G. Special Permutation(构造)
1、题目 G. Special Permutation 这道题的意思是给我们从111到nnn的排列,然后我们对这个排列的顺序上进行调换,需要满足的条件是任意两个相邻元素的绝对值的差满足条件:2≤∣pi−pi1∣≤42\leq |p_i-p_{i 1}|\leq 42≤∣pi−pi1∣≤4 …...
QML动态对象管理
QML中有多种方式来动态创建和管理QML对象: Loader (加载器)Repeater(复制器)ListView,GridWiew,PethView(视图) (之后会介绍)使用加载器ÿ…...

cmake入门03 -自定义find外部库
自定义检测外部库使用pkg-config查找库搜索.pc配置文件cmake函数链接到库自定义find库检测外部库的便捷方法:使用CMake自带的find-module使用<package>Config.cmake, <package>ConfigVersion.cmake和<package>Targets.cmake。这些文件由软件商提供…...
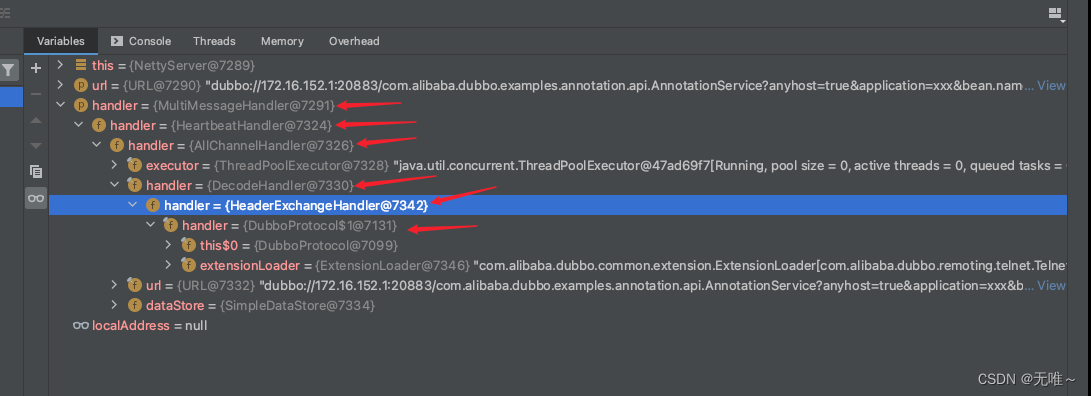
Dubbo源码解析-——服务导出
前言 在之前我们讲过Spring和Dubbo的集成,我们在服务上标注了DubboService的注解,然后最终Dubbo会调用到ServiceBean#export方法中,本次我们就来剖析下服务导出的全流程。 一、前置回顾 由于ServiceBean实现了ApplicationListener接口&…...

vue+django+neo4j 基于知识图谱红楼梦问答系统
vuedjangoneo4j 基于知识图谱红楼梦问答系统 项目背景 知识图谱是一种以图谱形式描述客观世界中存在的各种实体、概念及其关系的技术, 广泛应用于智能搜索、自动问答和决策支持等领域. 可视分析技术可以将抽象的知识图谱映射为图形元素, 帮助用户直观地感知和分析数据, 从而提…...

2023年全国最新食品安全管理员精选真题及答案13
百分百题库提供食品安全管理员考试试题、食品安全员考试预测题、食品安全管理员考试真题、食品安全员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 121.关于食品召回的说法,以下表述不正确的是(&am…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

PH热榜 | 2025-06-08
1. Thiings 标语:一套超过1900个免费AI生成的3D图标集合 介绍:Thiings是一个不断扩展的免费AI生成3D图标库,目前已有超过1900个图标。你可以按照主题浏览,生成自己的图标,或者下载整个图标集。所有图标都可以在个人或…...

【若依】框架项目部署笔记
参考【SpringBoot】【Vue】项目部署_no main manifest attribute, in springboot-0.0.1-sn-CSDN博客 多一个redis安装 准备工作: 压缩包下载:http://download.redis.io/releases 1. 上传压缩包,并进入压缩包所在目录,解压到目标…...

深入解析光敏传感技术:嵌入式仿真平台如何重塑电子工程教学
一、光敏传感技术的物理本质与系统级实现挑战 光敏电阻作为经典的光电传感器件,其工作原理根植于半导体材料的光电导效应。当入射光子能量超过材料带隙宽度时,价带电子受激发跃迁至导带,形成电子-空穴对,导致材料电导率显著提升。…...
