单元测试、集成测试、系统测试有什么不同?
单元测试、集成测试和系统测试是软件测试开发中不可或缺的部分。
单元测试:
-
范围:单元测试是对软件中最小的可测试单元的测试,通常是函数、方法或类。
-
目的:它的目标是验证每个单独的单元是否按照预期工作,以增加代码的可靠性和稳定性。
-
特点:单元测试通常由开发人员编写和执行,用于检查特定函数或方法对输入的处理和输出的结果是否正确。它们通常是自动化的,可以频繁地运行,并及早发现问题。
集成测试:
-
范围:集成测试是将已通过单元测试的组件组合在一起,并测试它们之间的交互。
-
目的:它的目标是检查不同组件之间的接口问题、通信问题和功能兼容性问题。通过集成测试,确保组件在合并到整个系统中时能够正确地协同工作。
-
特点:集成测试可以逐步的增加复杂度,测试系统中的子系统、模块或组件之间的相互作用。它们通常由开发团队或专门的集成测试团队编写和执行。
系统测试:
-
范围:系统测试是对整个软件系统进行的测试,包括所有的组件、模块和外部依赖。
-
目的:它旨在验证整个系统是否符合规范和需求,并检查其功能、性能、安全性、可靠性等方面。
-
特点:系统测试在一个模拟的真实环境中进行,以确保软件在用户使用环境中的正确运行。它涵盖了各种功能和用户场景,并检查系统是否满足用户的预期。
综上所述,单元测试针对代码中的最小功能单元,集成测试关注于组件之间的协作和兼容性,而系统测试则验证整个软件系统的完整性和性能。通过这三种测试的综合使用,可以有效地提高软件质量、稳定性。
软件测试持续集成?
在软件开发中,持续集成是一种将代码的集成和测试过程自动化的实践。它的目标是频繁地将开发人员的代码变更合并到主干分支,并自动构建、测试和部署应用程序。以下是一些实施持续集成的步骤和最佳实践:
-
使用版本控制系统:使用像Git这样的版本控制系统来跟踪代码的变更,确保开发人员可以方便地共享和合并代码。
-
自动化构建过程:创建一个自动化的构建过程,以编译和构建应用程序。这涉及到使用构建工具(如Maven、Gradle或Ant)来管理依赖项,并执行必要的构建任务。
-
编写自动化测试:编写全面的自动化测试套件,包括单元测试、集成测试和系统测试。这些测试应该覆盖代码的各个功能和路径,以确保代码的质量和稳定性。
-
设置持续集成服务器:配置一个持续集成服务器,例如Jenkins、Travis CI或GitLab CI。该服务器将监视代码库中的变更,并自动触发构建和测试过程。
-
频繁地提交代码:开发人员应该经常提交他们的代码变更,推荐每天多次。这有助于减少代码合并的复杂性,并使问题能够更早地被发现和解决。
-
自动化部署:在通过测试的代码变更后,自动部署应用程序到目标环境(如开发、测试或生产环境)。这可以使用自动化部署工具(例如Docker、Ansible或Kubernetes)来实现。
-
结果反馈和监测:持续集成服务器应该能够向团队成员提供构建和测试结果的反馈。这些结果包括编译错误、测试失败等。此外,可以设置监控和告警系统,以及日志记录来捕获潜在的问题和故障。
通过实施持续集成,可以加速软件开发过程,提高代码质量,并让团队更快地检测和解决问题。确保每次代码变更都经过全面的测试和验证。
最后:下方这份完整的软件测试视频教程已经整理上传完成,需要的朋友们可以自行领取【保证100%免费】

软件测试面试文档
我们学习必然是为了找到高薪的工作,下面这些面试题是来自阿里、腾讯、字节等一线互联网大厂最新的面试资料,并且有字节大佬给出了权威的解答,刷完这一套面试资料相信大家都能找到满意的工作。


相关文章:

单元测试、集成测试、系统测试有什么不同?
单元测试、集成测试和系统测试是软件测试开发中不可或缺的部分。 单元测试: 范围:单元测试是对软件中最小的可测试单元的测试,通常是函数、方法或类。 目的:它的目标是验证每个单独的单元是否按照预期工作,以增加代码…...
数据迁移DTS | 云上MySQL 数据库迁移至达梦数据库
引入 云上 MySQL 数据库 —> 向达梦国产化数据库迁移 下载&安装 达梦客户端工具 DM->可参考之前国产化专栏达梦文章 创建模式 在客户端分别依次执行以下命令脚本(这里没有通过客户端管理工具去创建达梦数据库的模式,当然也可以通过图形化界…...

Linux进程管理:(二)进程调度原语
文章说明: Linux内核版本:5.0 架构:ARM64 参考资料及图片来源:《奔跑吧Linux内核》 Linux 5.0内核源码注释仓库地址: zhangzihengya/LinuxSourceCode_v5.0_study (github.com) 进程调度的概念比较简单,…...

Compose 介绍
Compose 介绍 Android Compose 是 Google 官方推出的用于构建原生 Android UI 的现代工具包。它使用 Kotlin 语言编写,可以帮助开发人员更轻松、更快速地创建精美、响应式和高性能的 Android 应用。 Compose 的优势 声明式 UI: Compose 使用声明式 UI…...

5分钟搞定Python中函数的参数
函数的灵活性非常高,除了常规定义的位置参数以外,还支持默认参数、关键字参数、以及可变参数 ... 这样以来,不但能应对各种复杂的情况,甚至还可以简化调用者的代码。 位置参数 在调用函数时,一般会根据函数定义的参数…...
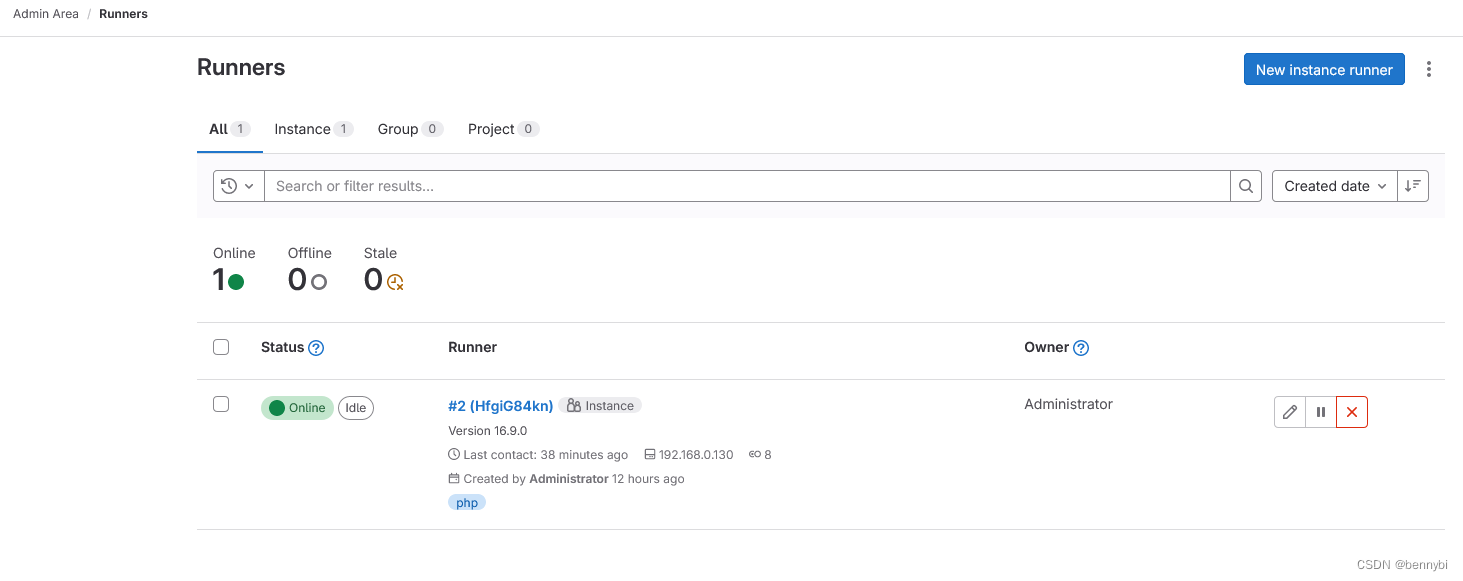
Gitlab: 私有化部署
目录 1. 说明 2. 资源要求 3. 安装 4. 配置实践 4.1 服务器 4.2 人员与项目 4.2 部署准备 4.2.1 访问变量及用户账号设置 4.2.2 Runner设置 4.2.3 要点 5. 应用项目 CI/CD 6. 参考 1. 说明 gitlab是一个强大且免费的代码管理/部署工具,能统一集成代码仓…...

深入理解Linux线程(LWP):概念、结构与实现机制(2)
🎬慕斯主页:修仙—别有洞天 ♈️今日夜电波:会いたい—Naomile 1:12━━━━━━️💟──────── 4:59 🔄 ◀️ ⏸ ▶️ ☰ &a…...

VBS脚本搞定,快速批量提取一堆Excel文件中的数据
1.需求诞生 小王就职于一家国有大型企业,工作业务十分繁忙,在处理企业某业务数据时,需要从上千个Excel文件中提取某一单元格位置的数据,并整理到另一个Excel文件。要说是这样的Excel文件仅有几个或者十几个也还好,手动…...
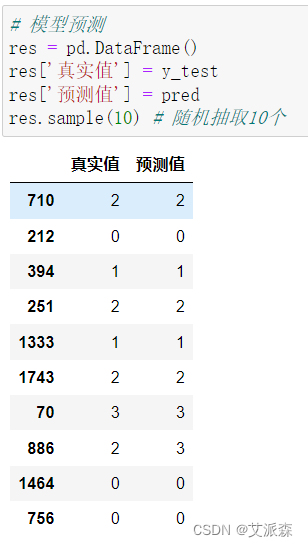
大数据分析案例-基于SVM支持向量机算法构建手机价格分类预测模型
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...

WPF 滑动条样式
效果图: 浅色: 深色: 滑动条部分代码: <Style x:Key"RepeatButtonTransparent" TargetType"{x:Type RepeatButton}"><Setter Property"OverridesDefaultStyle" Value"true"/&g…...

论文设计任务书学习文档|基于Web的个性化简历职位推荐系统的设计与实现
文章目录 论文(设计)题目:基于Web的个性化简历职位推荐系统的设计与实现1、论文(设计)的主要任务及目标2、论文(设计)的主要内容3、论文(设计)的基本要求4、进度安排论文(设计)题目:基于Web的个性化简历职位推荐系统的设计与实现 1、论文(设计)的主要任务及目标…...

Win11系统安装安卓子系统教程
随着Win11系统的不断普及,以及硬件设备的更新换代,我相信很多同学都已经更新并使用到了最新的Win11系统。那么,Win11系统最受期待的功能“Windows Subsystem for Android”(简称WSA),即《安卓子系统》。他可…...
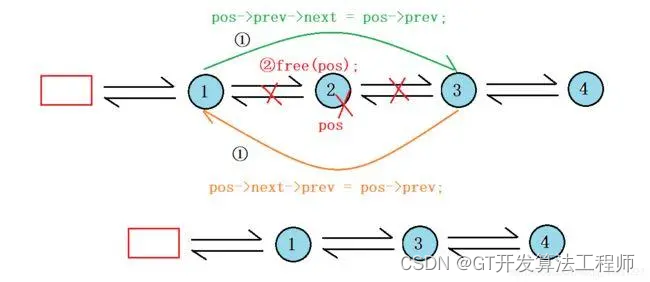
Python实现双向链表:从基础到应用
一、引言 双向链表是一种比单向链表更复杂的数据结构,每个节点除了包含数据和指向下一个节点的指针外,还包含一个指向前一个节点的指针。这种结构使得我们可以从链表的任何节点开始,向前或向后遍历链表。 目录 一、引言 二、节点定义 三、…...

c# 读取DataGridView中的数据
/// <summary> /// 读取DataGridView中的数据 /// </summary> /// <param name"dgv">DataGridView对象</param> /// <returns>DataTable对象</returns> private DataTable GetDgvToTab…...
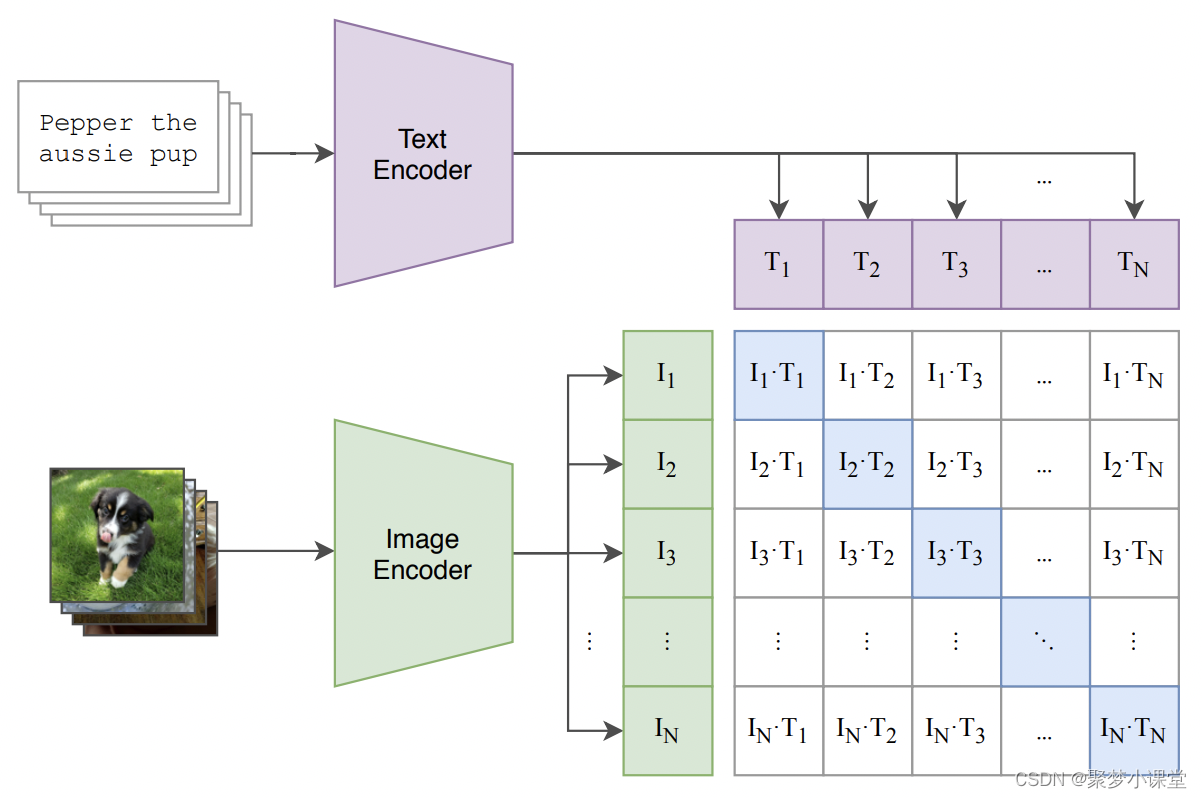
Stable Diffusion中的Clip模型
基础介绍 Stable Diffusion 是一个文本到图像的生成模型,它能够根据用户输入的文本提示(prompt)生成相应的图像。在这个模型中,CLIP(Contrastive Language-Image Pre-training)模型扮演了一个关键的角色&a…...

Python批量提取文件夹中图片的名称及路径到指定的.txt文件中
目录 一、代码二、提取效果 一、代码 import os# 定义要保存的文件名 file_name "TestImage/Image_Visible_Gray.txt"# 读取文件夹路径 folder_path "TestImage/Image_Visible_Gray"# 遍历文件夹中的所有文件 with open(file_name, "w") as f…...
微软开源 SBOM 生成工具:sbom-tool下载及使用详解
github地址 GitHub - microsoft/sbom-tool: The SBOM tool is a highly scalable and enterprise ready tool to create SPDX 2.2 compatible SBOMs for any variety of artifacts.The SBOM tool is a highly scalable and enterprise ready tool to create SPDX 2.2 compatib…...

【办公类-18-03】(Python)中班米罗可儿证书批量生成打印(班级、姓名)
作品展示——米罗可儿证书打印幼儿姓名 背景需求 2024年3月1日,中4班孩子一起整理美术操作材料《米罗可儿》的操作本——将每一页纸撕下来,分类摆放、确保纸张上下位置正确。每位孩子们都非常厉害,不仅完成了自己的一本,还将没有…...
)
js【详解】数据类型原理(含变量赋值详解-浅拷贝)
JavaScript 中的数据按存储方式的不同,分为值类型和引用类型。 值类型(共 6 种):赋值的时候传值 —— 数字、字符串、布尔值、null 、undefined,Symbol引用类型(仅 1 种):赋值的时候…...

SAM 影像分割——地理空间数据的分段模型的数据调参和自动分割分析
本笔记本展示了如何使用 Segment Anything Model (SAM) 从图像中分割对象,只需几行代码即可完成。 请确保在本笔记本中使用 GPU 运行时。对于 Google Colab,请转到运行时 -> 更改运行时类型,然后选择 GPU 作为硬件加速器。 地理空间数据的分段模型 Segment Anything M…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...
