【C++】平衡二叉搜索(AVL)树的模拟实现
一、 AVL树的概念
map、multimap、set、multiset 在其文档介绍中可以发现,这几个容器有个共同点是:其底层都是按照二叉搜索树来实现的,但是二叉搜索树有其自身的缺陷,假如往树中插入的元素有序或者接近有序,二叉搜索树就会退化成单支树,时间复杂度会退化成O(N)O(N)O(N),因此map、set等关联式容器的底层结构是对二叉树进行了平衡处理,即采用平衡树来实现。
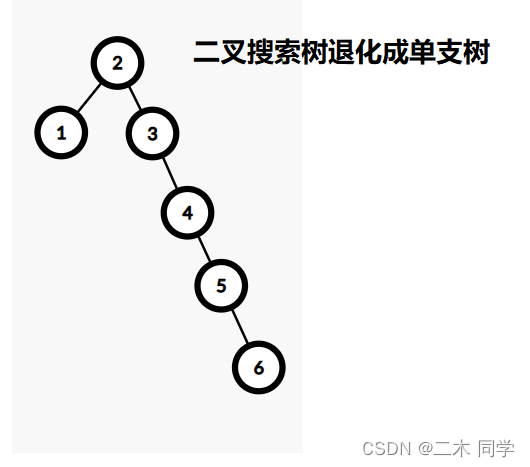
二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元素,效率低下。
因此,两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年
发明了一种解决上述问题的方法:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。
一棵AVL树或者是空树,或者是具有以下性质的二叉搜索树:
- 它的左右子树都是AVL树
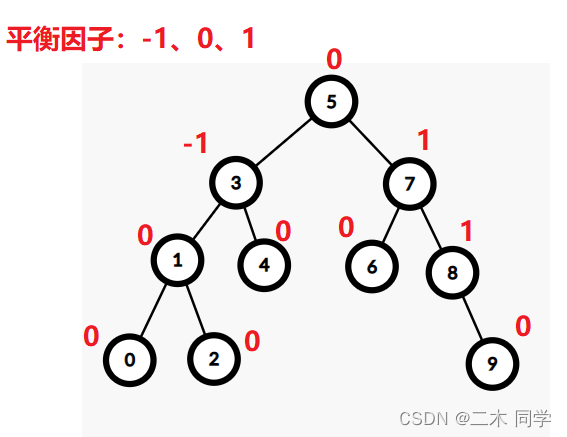
- 左右子树高度之差(简称平衡因子,balance factor)的绝对值不超过1(-1/0/1)
如果一棵二叉搜索树是高度平衡的,它就是AVL树。如果它有n个结点,其高度可保持在O(log2n)O(log_2 n)O(log2n),搜索时间复杂度O(log2nlog_2 nlog2n)。
二、AVL树节点的定义
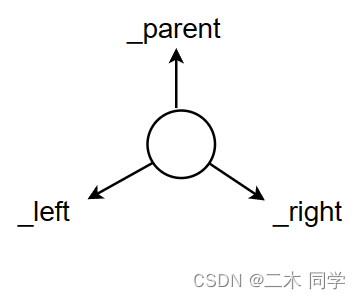
AVL树的节点是三叉链结构:即parent、left和right,它们分别指向当前节点的父节点、左子节点和右子节点。通过这种方式,可以在O(1)O(1)O(1)的时间内找到一个节点的父节点、左子节点和右子节点。
namespace AVL
{template<class K, class V>struct AVLTreeNode {AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent; //指向父节点的指针pair<K, V> _kv;int _bf; // 平衡因子AVLTreeNode(const pair<K, V>& kv) :_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_bf(0){}};template<class K, class V>class AVLTree{typedef AVLTreeNode<K, V> Node;public:private:Node* _root = nullptr;};
}
三、AVL树的插入
AVL树就是在二叉搜索树的基础上引入了平衡因子,因此AVL树也可以看成是二叉搜索树。那么AVL树的插入过程可以分为两步:
- 按照二叉搜索树的方式插入新节点
- 调整节点的平衡因子
插入在左平衡因子-1,插入在右平衡因子+1
是否继续更新的依据:parent所在子树的高度是否变化
-
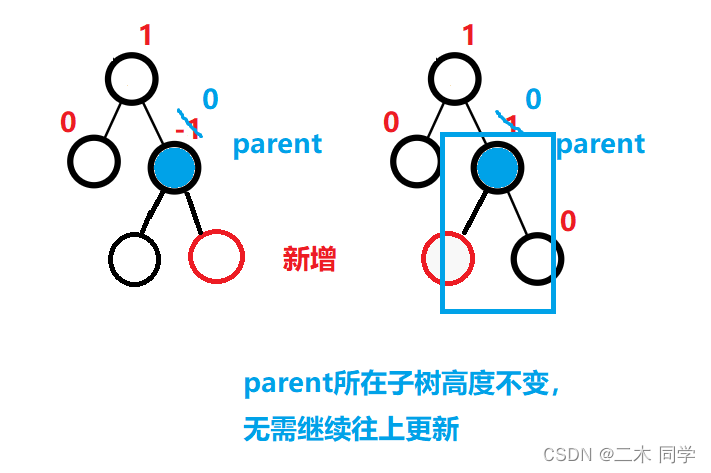
parent->_bf == 0说明之前parent->_bf是 1 或者 -1 说明之前parent一边高一边低,这次插入填上矮的那边,parent所在子树高度不变,不需要继续往上更新
-
parent->_bf == 1或-1说明之前是parent->_bf = 0,两边一样高,现在插入一边更高了,parent所在子树高度变了,继续往上更新
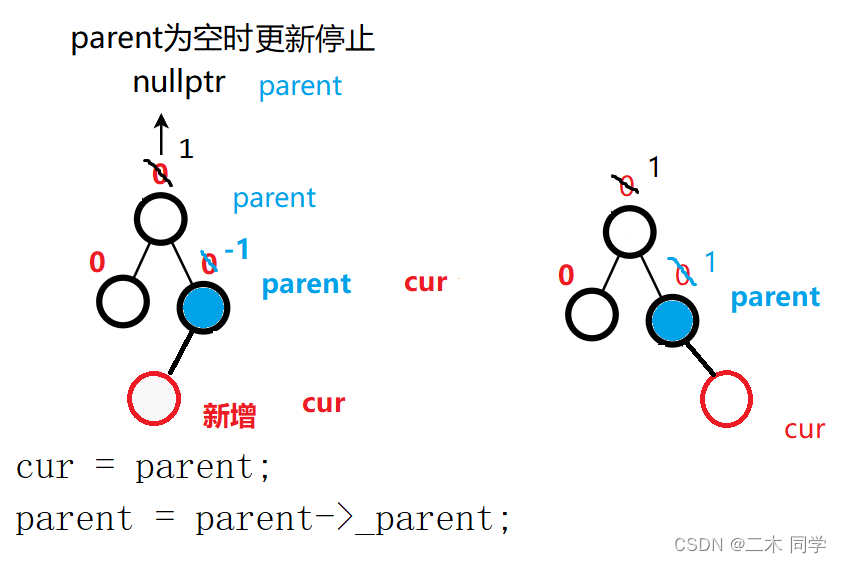
-
parent->_bf == 2或-2,说明之前parent->_bf == 1或者-1,现在插入严重不平衡,违反规则,就地处理–旋转
bool insert(const pair<K, V>& kv)
{// 1. 先按照二叉搜索树的规则将节点插入到AVL树中// 空树直接构建根if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (kv.first > cur->_kv.first) // 大了往右边走{parent = cur;cur = cur->_right;}else if (kv.first < cur->_kv.first) // 小了往左边走{parent = cur;cur = cur->_left;}else{return false;// 相等不插入}}//开始插入cur = new Node(kv);// 新插入的节点// 小的插入左,大的插入右if (kv.first < parent->_kv.first){parent->_left = cur;cur->_parent = parent;// 三叉链,不要忘记更新父指针}else{parent->_right = cur;cur->_parent = parent;}// 2. 新节点插入后,AVL树的平衡性可能会遭到破坏// 此时需要更新平衡因子,并检测是否破坏了AVL树的平衡性while (parent) // parent为空,也就更新到根停止{// 更新平衡因子// 新增在左,parent->bf--;// 新增在右,parent->bf++;if (cur == parent->_left){parent->_bf--;}else{parent->_bf++;}//检测平衡因子if (parent->_bf == 0){break;// 无需继续更新}else if (parent->_bf == 1 || parent->_bf == -1){// 插入前parent的平衡因子是0,插入后parent的平衡因为为1 或者 - 1 ,说明以parent为根的二叉树// 的高度增加了一层,因此需要继续向上调整cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){// parent的平衡因子为-2/2,违反了AVL树的平衡性// 需要对以 parent 为根的树进行 旋转 处理// 旋转break; // 旋转完成后,原 parent 为根的子树高度降低,已经平衡,不需要再向上更新}else{assert(false); // 平衡因子异常:绝对值大于2}}return true;
}
四、AVL树的旋转
在一棵原本是平衡的AVL树中插入一个新节点,可能造成不平衡,此时可通过旋转调整树的结构,使之平衡化。
旋转的目的:
- 让这颗子树左右高度不超过1
- 旋转过程中继续保持是搜索树
- 更新调整孩子节点的平衡因子
- 让这颗子树的高度跟插入前保持一致
根据节点插入位置的不同,AVL树的旋转分为四种:
- 新节点插入 较高 左左左子树的左左左侧—左左:右单旋
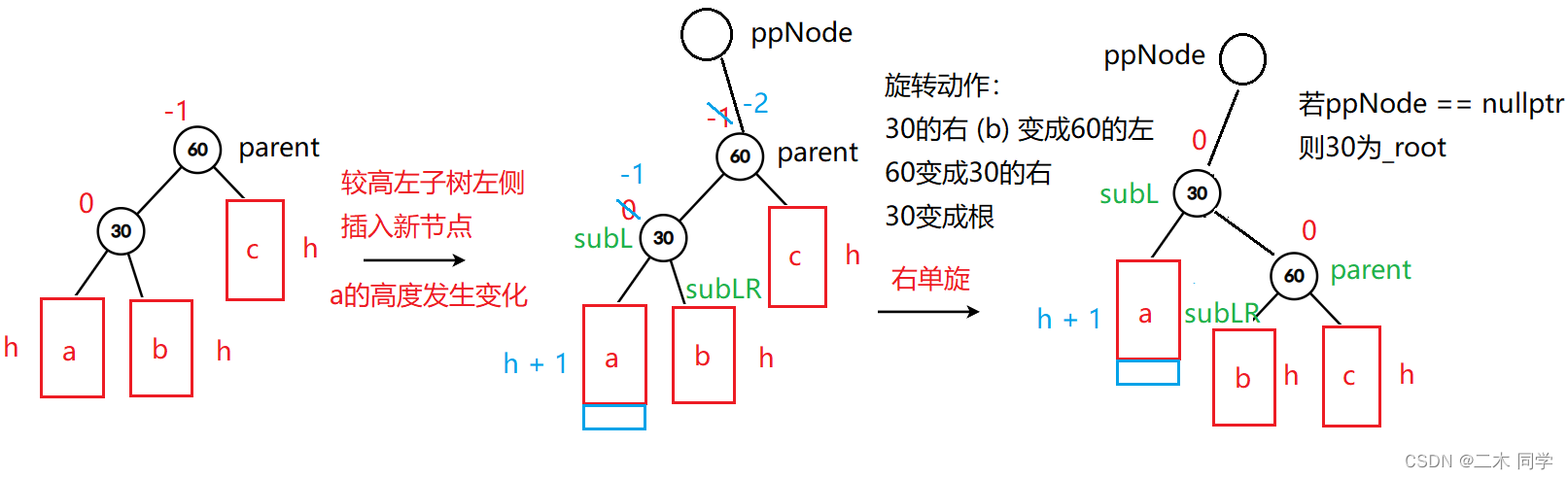
在插入前,图中AVL树是平衡的,新节点插入到30的左子树(注意:此处不是左孩子,图中a/b/c是高度为 h 的AVL子树)中,30左子树增加了一层,导致以60为根的二叉树不平衡
要让60平衡,只能将60左子树的高度减少一层,右子树增加一层,即将左子树往上提,这样60转下来,因为60比30大,只能将其放在30的右子树,而如果30有右子树,右子树根的值一定大于30,小于60,只能将其放在60的左子树,旋转完成后,更新节点的平衡因子即可。
在旋转过程中,有以下几种情况需要考虑:
- 30节点的右孩子可能存在,也可能不存在
- 60可能是根节点,也可能是子树,如果是根节点,旋转完成后,要更新根节点,如果是子树,可能是某个节点的左子树,也可能是右子树
这里举一些详细的例子进行画图,考虑各种情况,加深旋转的理解
h == 0,则a/b/c是空树:
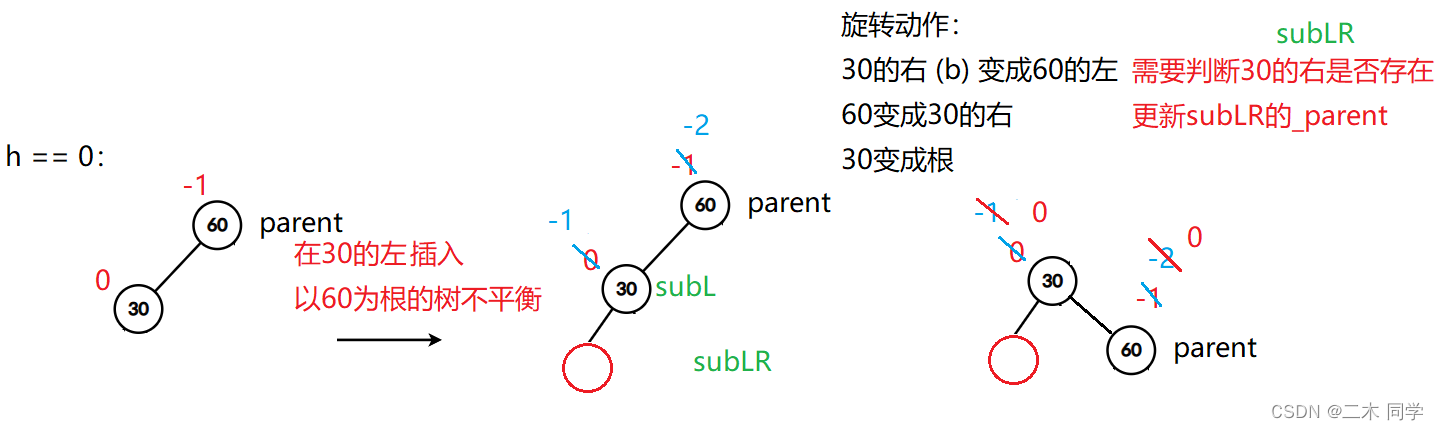
h == 1:
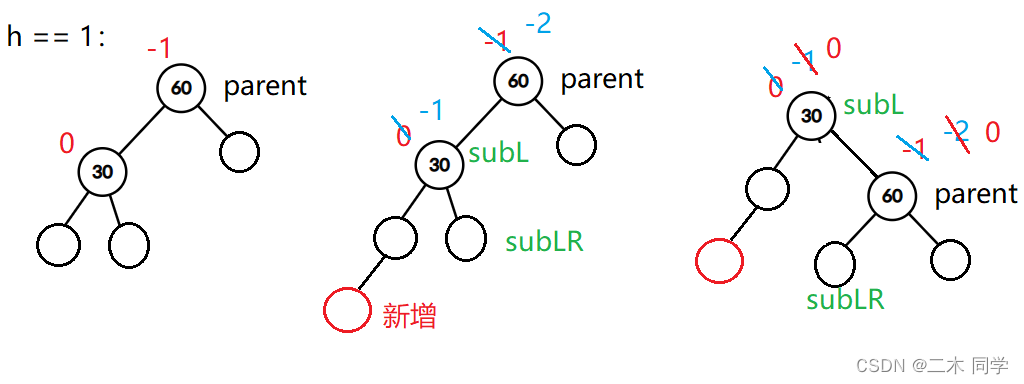
h == 2的情况已经有很多种了,随着h的增加情况会越来越复杂
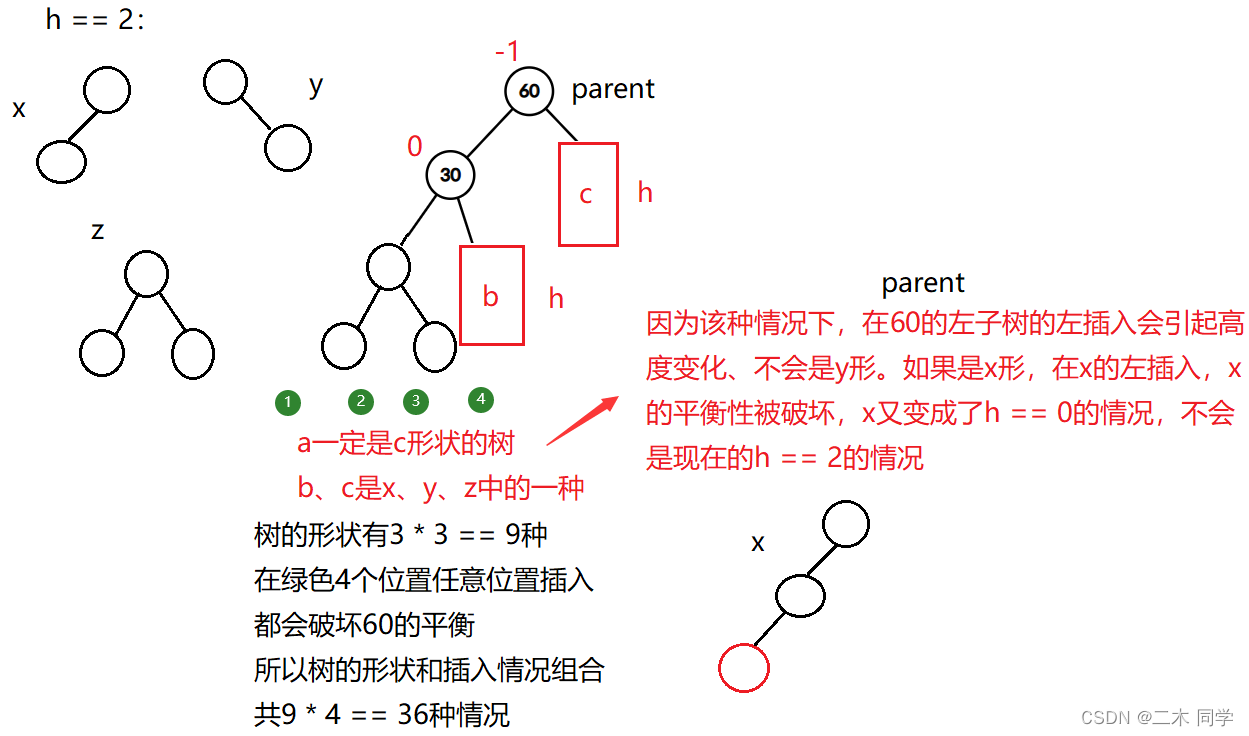
看图写代码:
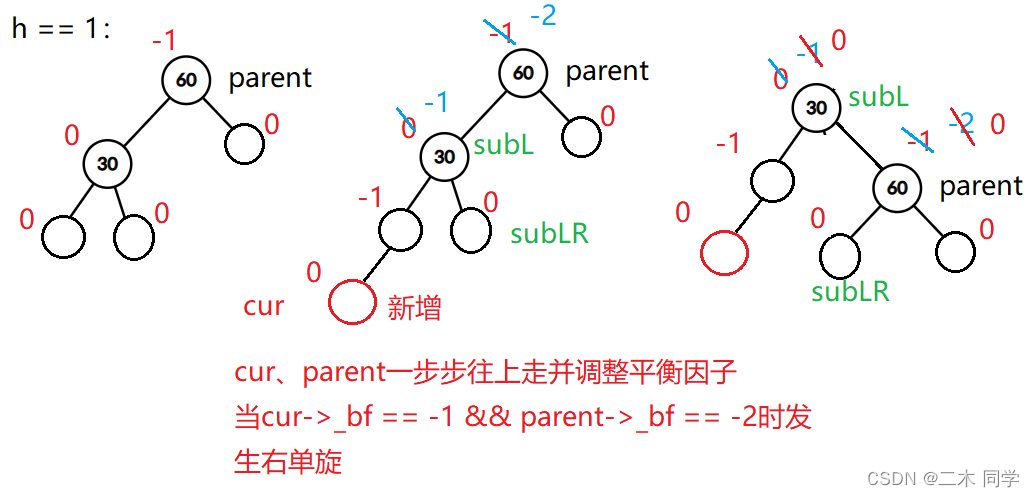
void RotateR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;// 30的右变成60的左parent->_left = subLR;if (subLR != nullptr) // 30的右不为空,更新_parent指针{subLR->_parent = parent;}Node* ppNode = parent->_parent;// 60变成30的右parent = subL->_right;parent->_parent = subL;//不要忘记更新parent的父指针if (_root == parent) // parent就是根//if (ppNode == nullptr) //也可以使用这个判断条件{_root = subL;_root->_parent = nullptr;}else // parent是左或右子树{// parent是左就把subL链接到左,是右就链接到右if (parent == ppNode->_left){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;// 同样不要忘记更新subL的父指针}// 最后更新parent和subL的平衡因子parent->_bf = subL->_bf = 0;
}- 新节点插入较高右右右子树的右右右侧—右右:左单旋
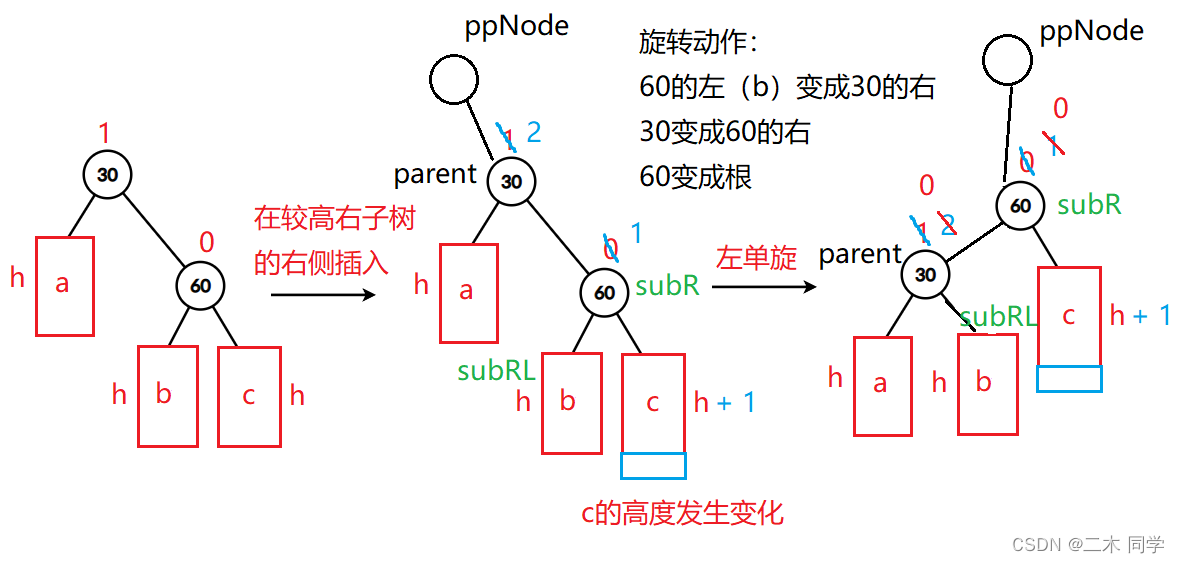
左单旋实现及情况考虑可参考右单旋
h == 0的情况:
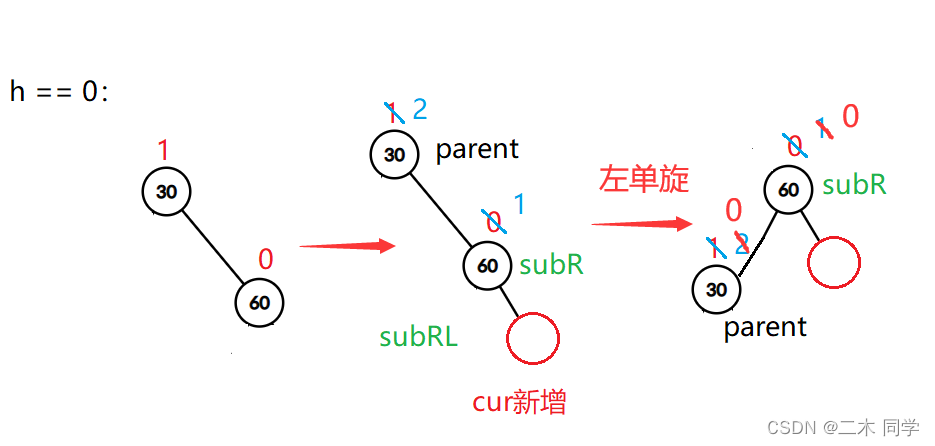
h == 1:
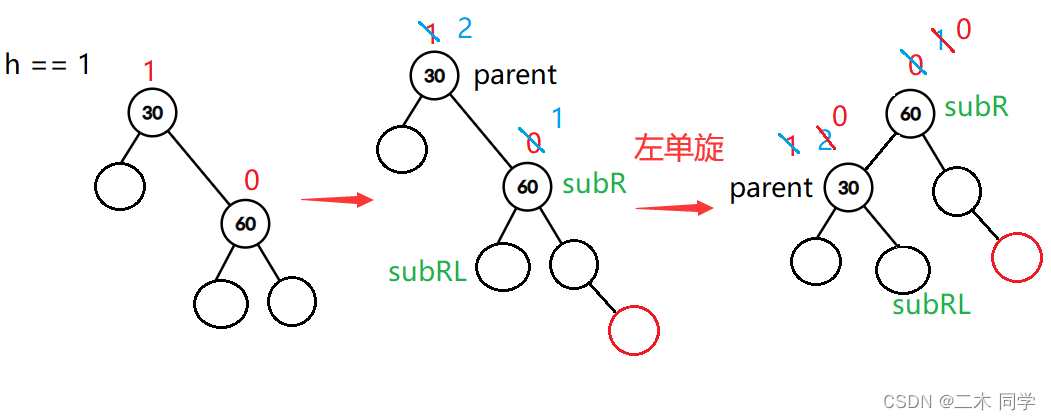
void RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;// 60的左变成30的右parent->_right = subRL;// 更新subRL的父指针if (subRL){subRL->_parent = parent;}Node* ppNode = parent->_parent;// 30变成60的左subR->_left = parent;parent->_parent = subR;//if (_root == parent)if (ppNode == nullptr){_root = subR;_root->_parent = nullptr;}else{if (parent == ppNode->_left){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_parent = ppNode;}parent->_bf = subR->_bf = 0;
}
像下图的情况简单的单旋已经不能正确调整平衡,需要使用双旋(不同轴点的单旋):
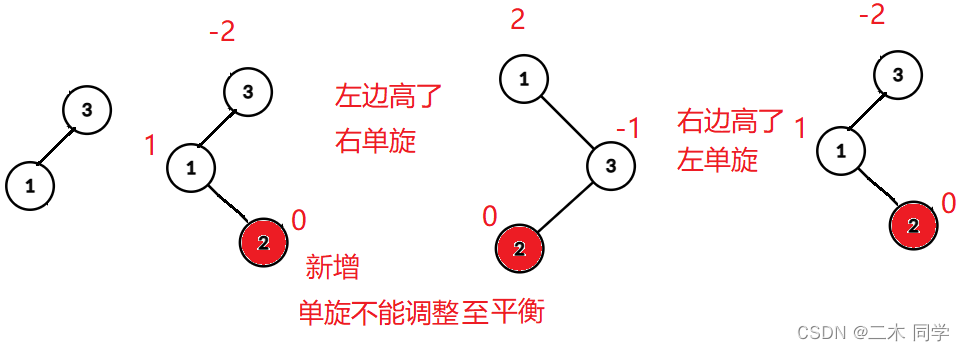
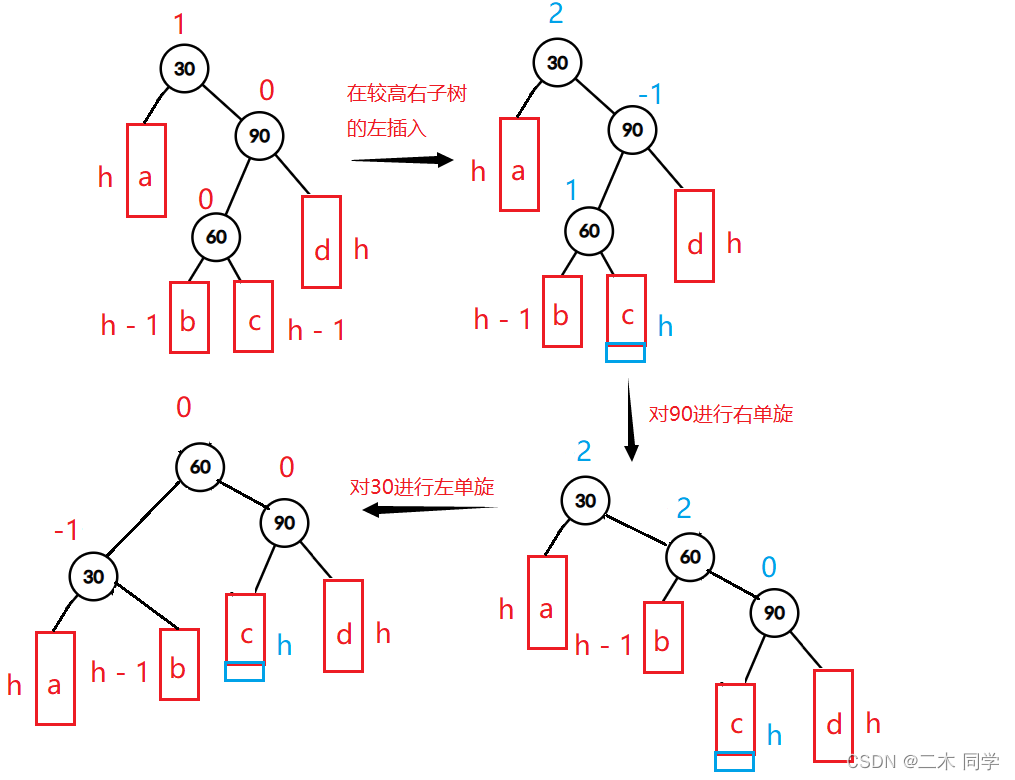
- 新节点插入较高左左左子树的右右右侧—左右:先左单旋再右单旋
a/d是高度为 h 的AVL树
b/c是高度为 h - 1 的AVL树
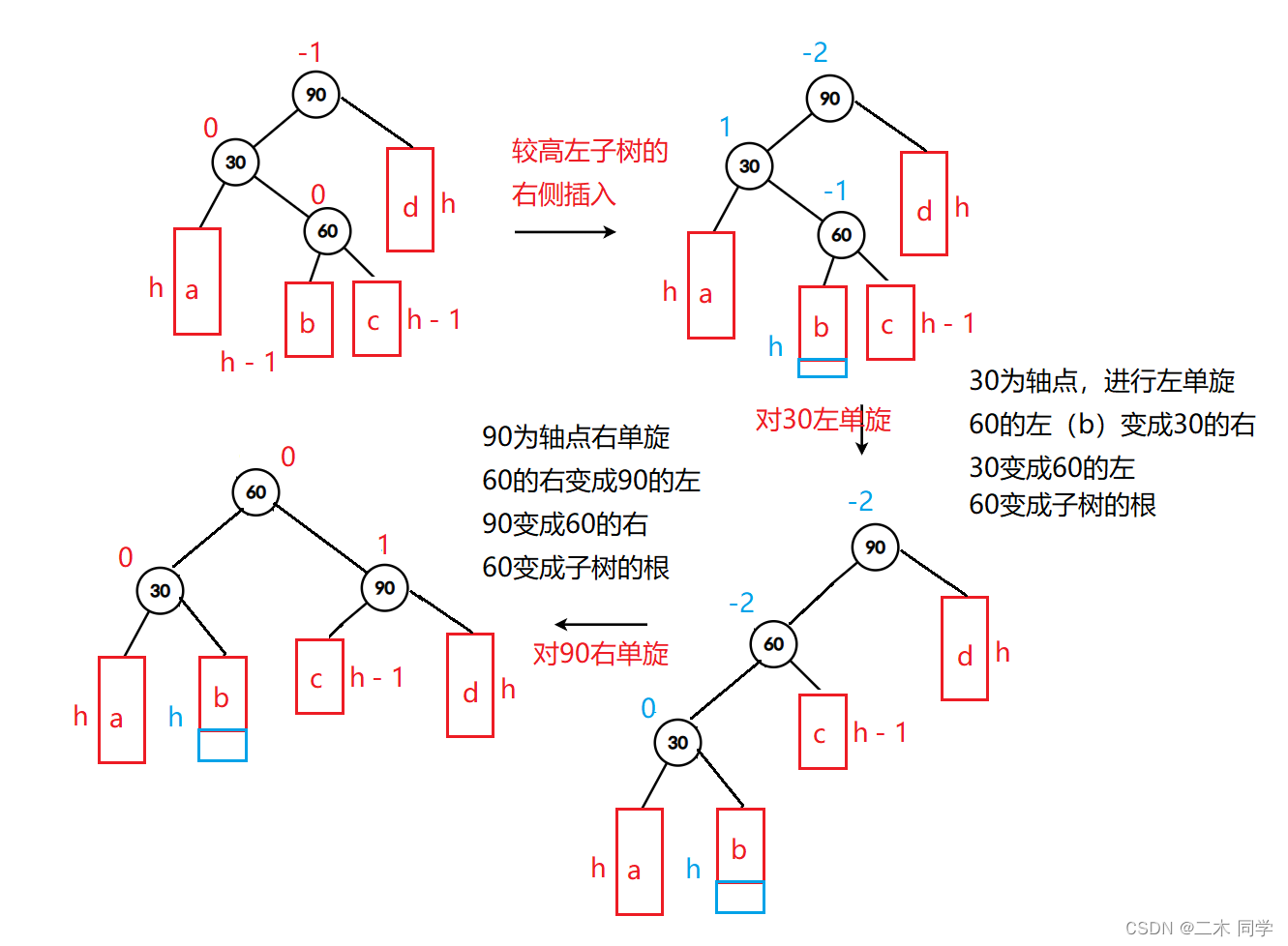
h == 0:
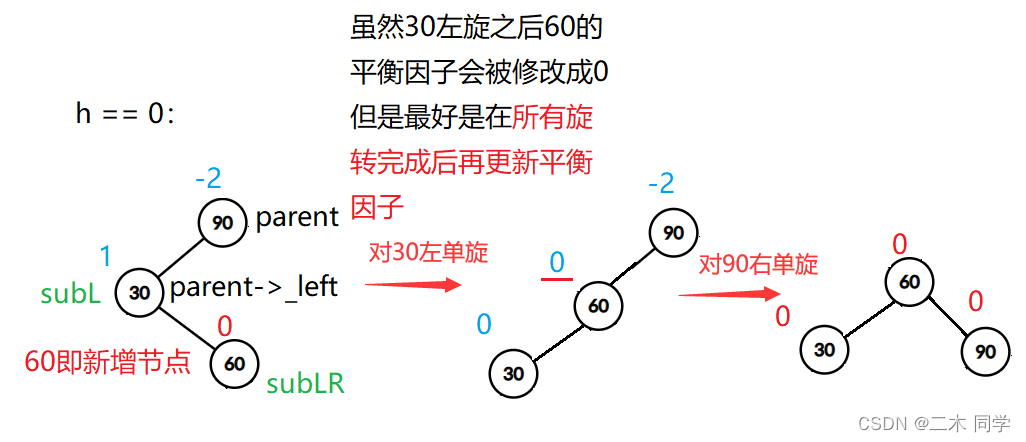
h == 1:
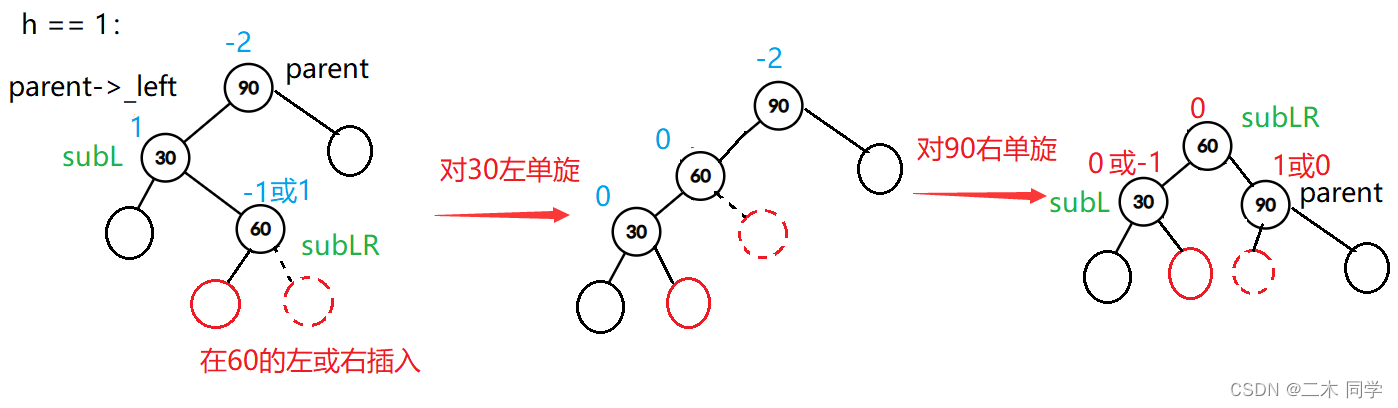
看图写代码:
void RotateLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;// 对30左单旋,对90右单旋RotateL(parent->_left);RotateR(parent);// 最后更新平衡因子if (bf == 0) // subLR自己是新增{parent->_bf = 0;subL->_bf = 0;subLR->_bf = 0;}else if (bf == -1) // 在subLR的左新增{parent->_bf = 1;subL->_bf = 0;subLR->_bf = 0;}else if (bf == 1) // 在subLR的右新增{parent->_bf = 0;subL->_bf = -1;subLR->_bf = 0;}else{assert(false);// 异常处理}
}
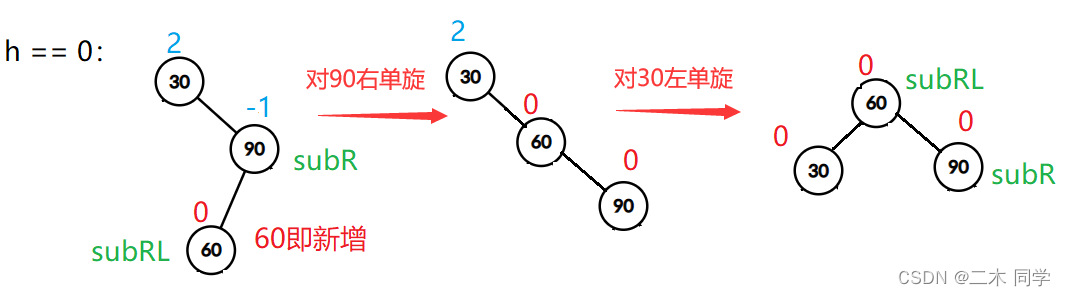
- 新节点插入较高右右右子树的左左左侧—右左:先右单旋再左单旋
h == 0:
h == 1:
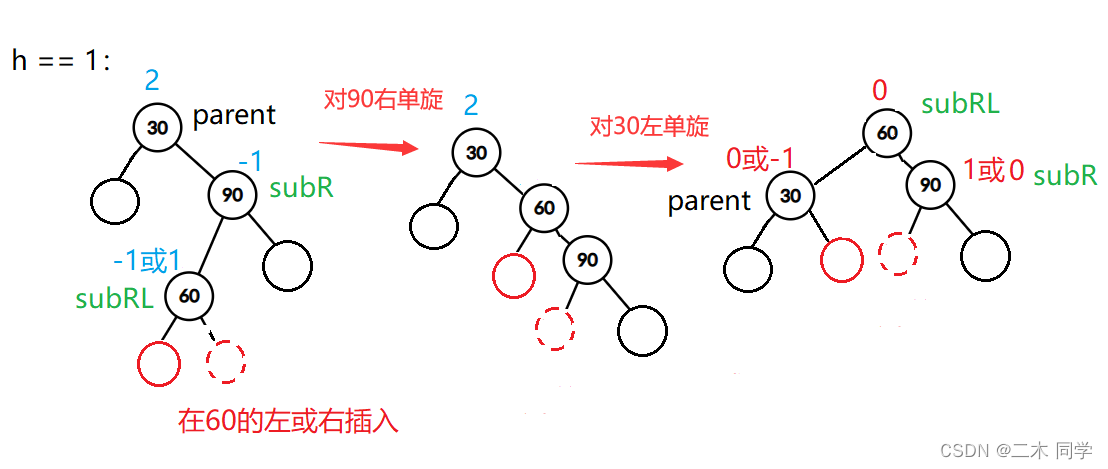
void RotateRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);if (bf == 0){parent->_bf = 0;subR->_bf = 0;subRL->_bf = 0;}else if (bf == -1){parent->_bf = 0;subR->_bf = 1;subRL->_bf = 0;}else if (bf == 1){parent->_bf = -1;subR->_bf = 0;subRL->_bf = 0;}else{assert(false);}
}
总结:
假如以 parent 为根的子树不平衡,即 parent 的平衡因子为 2 或者 -2 ,分以下情况考虑:
- parent 的平衡因子为 2,说明 parent 的右子树高,设 parent 的右子树的根为 subR
- 当 subR 的平衡因子为 1 时,执行左单旋
- 当 subR 的平衡因子为 -1 时,执行右左双旋
- parent 的平衡因子为 -2 ,说明 parent 的左子树高,设 parent的左子树的根为 subL
- 当 subL 的平衡因子为 -1 是,执行右单旋
- 当 subL 的平衡因子为 1 时,执行左右双旋
旋转完成后,原 parent 为根的子树高度降低,已经平衡,不需要再向上更新。
insert 时平衡因子检测的整体代码:
while (parent) // parent为空,也就更新到根停止
{// 更新平衡因子// 新增在左,parent->bf--;// 新增在右,parent->bf++;if (cur == parent->_left){parent->_bf--;}else{parent->_bf++;}//检测if (parent->_bf == 0){break;// 无需继续更新}else if (parent->_bf == 1 || parent->_bf == -1){// 插入前parent的平衡因子是0,插入后parent的平衡因为为1 或者 - 1 ,说明以parent为根的二叉树// 的高度增加了一层,因此需要继续向上调整cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){// parent的平衡因子为-2/2,违反了AVL树的平衡性// 需要对以 parent 为根的树进行 旋转 处理if (parent->_bf == -2 && cur->_bf == -1) // 右单旋{RotateR(parent);}else if (parent->_bf == 2 && cur->_bf == 1) // 左单旋{RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == 1) // 左右双旋{RotateLR(parent);}else if (parent->_bf == 2 && cur->_bf == -1) // 右左双旋{RotateRL(parent);}else{assert(false);// 平衡因子异常}break; // 旋转完成后,原 parent 为根的子树高度降低,已经平衡,不需要再向上更新}else{assert(false); // 平衡因子异常:绝对值大于2}
}
AVL树的整体代码:AVL树的简单模拟实现
五、AVL树的验证
AVL树是在二叉搜索树的基础上加入了平衡性的限制,因此要验证AVL树,可以分两步:
- 验证其为二叉搜索树
如果中序遍历可得到一个有序的序列,就说明为二叉搜索树 - 验证其为平衡树
每个节点子树高度差的绝对值不超过1(注意节点中如果有平衡因子,还需验证节点的平衡因子是否计算正确
int Height(Node* root)
{if (root == nullptr)return 0;int lh = Height(root->_left);int rh = Height(root->_right);return lh > rh ? lh + 1 : rh + 1;
}bool IsBalance()
{return IsBalance(_root);
}bool IsBalance(Node* root)
{if (root == nullptr){return true;}int leftHeight = Height(root->_left);int rightHeight = Height(root->_right);if (rightHeight - leftHeight != root->_bf){std::cout << root->_kv.first << " 平衡因子异常" << std::endl;return false;}return abs(rightHeight - leftHeight) < 2&& IsBalance(root->_left)&& IsBalance(root->_right);
}
六、AVL树的性能
AVL树是一棵绝对平衡的二叉搜索树,其要求每个节点的左右子树高度差的绝对值都不超过1,这样可以保证查询时高效的时间复杂度,即log2(N)log_2 (N)log2(N)。
但是如果要对AVL树做一些结构修改的操 作,性能非常低下,比如:插入时要维护其绝对平衡,旋转的次数比较多,更差的是在删除时,有可能一直要让旋转持续到根的位置。因此:如果需要一种查询高效且有序的数据结构,而且数据的个数为静态的(即不会改变),可以考虑AVL树,但一个结构经常修改,就不太适合。
相关文章:

【C++】平衡二叉搜索(AVL)树的模拟实现
一、 AVL树的概念 map、multimap、set、multiset 在其文档介绍中可以发现,这几个容器有个共同点是:其底层都是按照二叉搜索树来实现的,但是二叉搜索树有其自身的缺陷,假如往树中插入的元素有序或者接近有序,二叉搜索树…...
[2019红帽杯]childRE
题目下载:下载 参考:re学习笔记(24)BUUCTF-re-[2019红帽杯]childRE_Forgo7ten的博客-CSDN博客 这道题涉及到c函数的修饰规则,按照规则来看应该是比较容易理解的。上面博客中有总结规则,可以学习一下。 载…...
(附源码))
2D图像处理:九点标定_下(机械手轴线与法兰轴线不重合)(附源码)
文章目录 2. 机械手轴线与法兰轴线不重合2.1 两次拍照避免标定旋转中心2.2 旋转中心标定2.3 非标定中心的方法2.3.1 预备内容-点坐标旋转计算2.3.2 工件存在平移和旋转3. 代码(待更新)上一篇:2D图像处理:九点标定_上(机械手轴线与法兰轴线重合)(附源码) 2. 机械手轴线…...

【二分查找】分巧克力、机器人跳跃、数的范围
Halo,这里是Ppeua。平时主要更新C语言,C,数据结构算法......感兴趣就关注我吧!你定不会失望。 🌈个人主页:主页链接 🌈算法专栏:专栏链接 我会一直往里填充内容哒! &…...

Hyperf使用RabbitMQ消息队列
Hyperf连接使用RabbitMQ消息中间件 传送门 使用Docker部署RabbitMQ,->传送门<使用Docker部署Hyperf,->传送门-< 部署环境 安装amqp扩展 composer require hyperf/amqp安装command命令行扩展 composer require hyperf/command配置参数 假…...
【Linux】P3 用户与用户组
用户与用户组root 超级管理员设置超级管理员密码切换到超级管理员sudo 临时使用超级权限用户与用户组用户组管理用户管理getentroot 超级管理员 设置超级管理员密码 登陆后不会自动开启 root 访问权限,需要首先执行如下步骤设定 root 超级管理员密码 1、解除 roo…...

Spring核心模块——Aware接口
Aware接口前言基本内容例子结尾前言 Spring的依赖注入最大亮点是所有的Bean对Spring容器对存在都是没有意识到,Spring容器中的Bean的耦合度是很低的,我们可以将Spring容器很容易换成其他的容器。 但是实际开发的时候,我们经常要用到Spring容…...

Linux网络编程 第六天
目录 学习目标 libevent介绍 libevent的安装 libevent库的使用 libevent的使用 libevent的地基-event_base 等待事件产生-循环等待event_loop 使用libevent库的步骤: 事件驱动-event 编写一个基于event实现的tcp服务器: 自带buffer的事件-buff…...
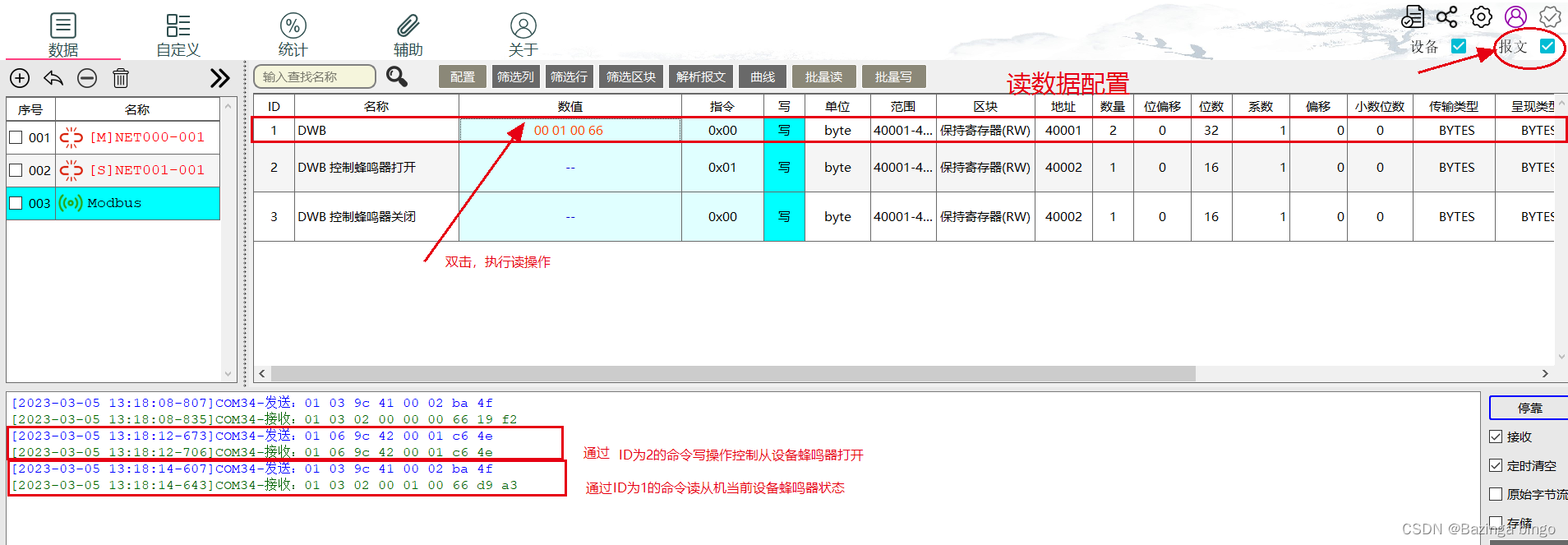
STM32开发(六)STM32F103 通信 —— RS485 Modbus通信编程详解
文章目录一、基础知识点二、开发环境三、STM32CubeMX相关配置1、STM32CubeMX基本配置2、STM32CubeMX RS485 相关配置四、Vscode代码讲解五、结果演示以及报文解析一、基础知识点 了解 RS485 Modbus协议技术 。本实验是基于STM32F103开发 实现 通过RS-485实现modbus协议。 准备…...

AcWing1049.大盗阿福题解
前言如果想看状态机的详解,点机这里:dp模型——状态机模型C详解1049. 大盗阿福阿福是一名经验丰富的大盗。趁着月黑风高,阿福打算今晚洗劫一条街上的店铺。这条街上一共有 N家店铺,每家店中都有一些现金。阿福事先调查得知,只有当…...

python日志模块,loggin模块
python日志模块,loggin模块loggin模块日志的格式处理器种类日志格式的参数使用loggin模块 logging库采用模块化方法,并提供了几类组件:记录器,处理程序,过滤器和格式化程序。 记录器(Logger)&a…...
接口自动化入门-TestNg
目录1.TestNg介绍2、TestNG安装3、TestNG使用3.1 编写测试用例脚本3.2 创建TestNG.xml文件(1)创建testng.xml文件(2)修改testng.xml4、测试报告生成1.TestNg介绍 TestNg是Java中开源的自动化测试框架,灵感来源于Junit…...

Spring AOP —— 详解、实现原理、简单demo
目录 一、Spring AOP 是什么? 二、学习AOP 有什么作用? 三、AOP 的组成 3.1、切面(Aspect) 3.2、切点(Pointcut) 3.3、通知(Advice) 3.4、连接点 四、实现 Spring AOP 一个简…...

(蓝桥真题)异或数列(博弈)
题目链接:P8743 [蓝桥杯 2021 省 A] 异或数列 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 样例输入: 4 1 1 1 0 2 2 1 7 992438 1006399 781139 985280 4729 872779 563580 样例输出: 1 0 1 1 分析:容易想到对于异或最大值…...

4万字数字政府建设总体规划方案WORD
本资料来源公开网络,仅供个人学习,请勿商用。部分资料内容: 我省“数字政府”架构 (一) 总体架构。 “数字政府”总体架构包括管理架构、业务架构、技术架构。其中,管理架构体现“管运分离”的建设运营模式…...

CCF/CSP 201709-2公共钥匙盒100分
试题编号:201709-2试题名称:公共钥匙盒时间限制:1.0s内存限制:256.0MB问题描述:问题描述 有一个学校的老师共用N个教室,按照规定,所有的钥匙都必须放在公共钥匙盒里,老师不能带钥…...

【OC】Blocks模式
1. Block语法 Block语法完整形式如下: ^void (int event) {printf("buttonId:%d event%d\n", i, event); }完整形式的Block语法与一般的C语言函数定义相比,仅有两点不同。 没有函数名。带有“^”(插入记号)。 因为O…...
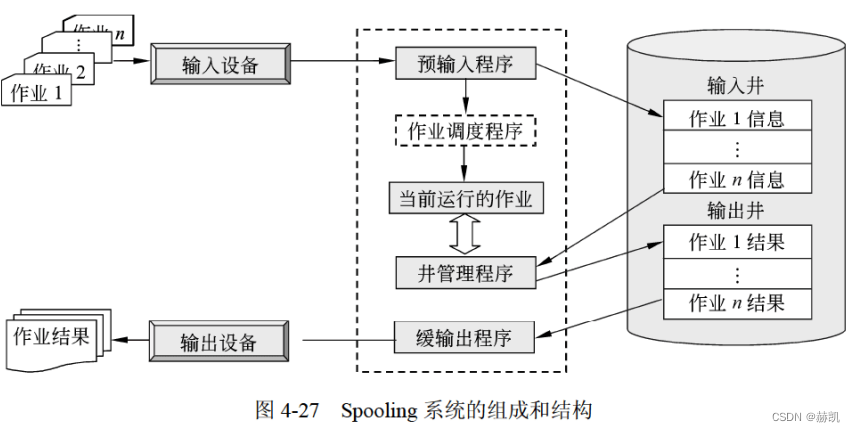
软件设计师教程(七)计算机系统知识-操作系统知识
软件设计师教程 软件设计师教程(一)计算机系统知识-计算机系统基础知识 软件设计师教程(二)计算机系统知识-计算机体系结构 软件设计师教程(三)计算机系统知识-计算机体系结构 软件设计师教程(…...

蓝桥杯2023/3/2
1. 小蓝正在学习一门神奇的语言,这门语言中的单词都是由小写英文字母组 成,有些单词很长,远远超过正常英文单词的长度。小蓝学了很长时间也记不住一些单词,他准备不再完全记忆这些单词,而是根据单词中哪个字母出现得最…...

【IoT】创业成功不可或缺的两个因素:能力和趋势
今天就来谈谈能力和趋势究竟哪个更重要的问题。 在谈成功的十大要素时,我曾经讲到: 一命、二运、三风水,这三个要素几乎不涉及任何个人的努力。 而趋势跟这三个要素又是息息相关的,这也类似雷军所说的飞猪理论。 只要风足够大&…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

快速排序算法改进:随机快排-荷兰国旗划分详解
随机快速排序-荷兰国旗划分算法详解 一、基础知识回顾1.1 快速排序简介1.2 荷兰国旗问题 二、随机快排 - 荷兰国旗划分原理2.1 随机化枢轴选择2.2 荷兰国旗划分过程2.3 结合随机快排与荷兰国旗划分 三、代码实现3.1 Python实现3.2 Java实现3.3 C实现 四、性能分析4.1 时间复杂度…...

TJCTF 2025
还以为是天津的。这个比较容易,虽然绕了点弯,可还是把CP AK了,不过我会的别人也会,还是没啥名次。记录一下吧。 Crypto bacon-bits with open(flag.txt) as f: flag f.read().strip() with open(text.txt) as t: text t.read…...
Android屏幕刷新率与FPS(Frames Per Second) 120hz
Android屏幕刷新率与FPS(Frames Per Second) 120hz 屏幕刷新率是屏幕每秒钟刷新显示内容的次数,单位是赫兹(Hz)。 60Hz 屏幕:每秒刷新 60 次,每次刷新间隔约 16.67ms 90Hz 屏幕:每秒刷新 90 次,…...

C++ 类基础:封装、继承、多态与多线程模板实现
前言 C 是一门强大的面向对象编程语言,而类(Class)作为其核心特性之一,是理解和使用 C 的关键。本文将深入探讨 C 类的基本特性,包括封装、继承和多态,同时讨论类中的权限控制,并展示如何使用类…...
JUC并发编程(二)Monitor/自旋/轻量级/锁膨胀/wait/notify/锁消除
目录 一 基础 1 概念 2 卖票问题 3 转账问题 二 锁机制与优化策略 0 Monitor 1 轻量级锁 2 锁膨胀 3 自旋 4 偏向锁 5 锁消除 6 wait /notify 7 sleep与wait的对比 8 join原理 一 基础 1 概念 临界区 一段代码块内如果存在对共享资源的多线程读写操作…...
