深度学习-神经网络原理
文章目录
- 神经网络原理
- 1.单层神经网络
- 1.1 回归单层神经网络:线性回归
- 1.2 二分类单层神经网络:sigmoid与阶跃函数
- 1.3 多分类单层神经网络:softmax回归
神经网络原理
人工神经网络(Artificial Neural Network,ANN),通常简称为神经网络,它是机器学习当中独树一帜的,最强大的强学习器没有之一。
人脑通过构建复杂的网络可以进行逻辑,语言,图像的学习,而传统机器学习算法不具备和人类相似的学习能力。机器学习研究者们相信,模拟大脑结构可以让机器的学习能力更上一层楼,于是人工神经网络算法应运而生,现在基本都简称为”神经网络“。有了神经网络,基于其算法延申出来的机器学习分枝学科——深度学习也从此走入了人们的视野,成为所有让世人惊叹的人工智能技术的根基。在深度学习中,我们使用圆来表示神经元,使用线表示数据流动的方向。

1.单层神经网络
1.1 回归单层神经网络:线性回归
了解神经网络,可以从线性回归算法开始。线性回归算法是机器学习中最简单的回归类算法,多元线性回归指的就是一个样本有多个特征的线性回归问题。对于一个有个特征的样本 而言,它的回归结果可以写作一个几乎人人熟悉的方程:
z i ^ = b + w 1 x i 1 + w 2 x i 2 + . . . + w n x i n \hat{z_i} = b + w_1x_{i1} + w_2x_{i2} + ... +w_nx_{in} zi^=b+w1xi1+w2xi2+...+wnxin
w w w和 b b b被统称为模型的参数,其中 b b b被称为截距(intercept),也叫做偏差(bias), w 1 w n w_1~w_n w1 wn被称为回归系数(regression coefficient),也叫作权重(weights)。这个表达式,其实就和我们小学时就无比熟悉的 y = a x + b y = ax+b y=ax+b是同样的性质。其中 y y y是我们的目标变量,也就是标签。
现在假设,我们的数据只有2个特征,则线性回归方程可以写作如下结构:
z ^ = b + x 1 w 1 + x 2 w 2 \hat{z} = b + x_1w_1 + x_2w_2 z^=b+x1w1+x2w2
此时,我们只要对模型输入特征 x 1 x_1 x1和 x 2 x_2 x2的取值,就可以得出对应的预测值 z ^ \hat{z} z^ 。在上一节中我们提到,神经网络的预测过程是从神经元左侧输入特征,让神经元处理数据,并从右侧输出预测结果。这个过程和我们刚才说到的线性回归输出预测值的过程是一 致的。如果我们使用一个神经网络来表达线性回归上的过程,则可以有:

在神经网络中,竖着排列在一起的一组神经元叫做“一层网络”,所以线性回归的网络直观看起来有两层,两层神经网络通过写有参数的线条相连。我们从左侧输入常数 1 1 1和特征取值 x 1 x_1 x1, x 2 x_2 x2,再让它们与相对应的参数相乘,就可以得到 b b b, w 1 x 1 w_1x_1 w1x1, w 2 x 2 w_2x_2 w2x2三个结果。这三个结果通过连接到下一层神经元的直线,被输入下一层神经元。我们在第二层的神经元中将三个乘积进行加和(使用符号 ∑ \sum ∑表示),就可以得到加和结果 z ^ \hat{z} z^,即 b + x 1 w 1 + x 2 w 2 b + x_1w_1 + x_2w_2 b+x1w1+x2w2,这个值正是我们的预测值。可见,线性回归方程与上面的神经网络图达到的效果是一模一样的。
在上述过程中,左侧的是神经网络的输入层(input layer)。输入层由众多承载数据用的神经元组成,数据从这里输入,并流入处理数据的神经元中。在所有神经网络中,输入层永远只有一层,且每个神经元上只能承载一个特征或一个常量。现在的二元线性回归只有两个特征,所以输入层上只需要三个神经元,包括两个特征和一个常量,其中这里的常量仅仅是被用来乘以偏差用的。对于没有偏差的线性回归来说,我们可以不设置常量1。
右侧的是输出层(output layer)。输出层由大于等于一个神经元组成,我们总是从这一层来获取预测结果。输出层的每个神经元上都承载着单个或多个功能,可以处理被输入神经元的数据。在线性回归中,这个功能就是“加和”,当我们把加和替换成其他的功能,就能够形成各种不同的神经网络。
在神经元之间相互连接的线表示了数据流动的方向,就像人脑神经细胞之间相互联系的“轴突”。在人脑神经细胞中,轴突控制电子信号流过的强度,在人工神经网络中,神经元之间的连接线上的权重也代表了”信息可通过的强度“。最简单的例子是,当 w 1 w_1 w1为0.5时,在特征 x 1 x_1 x1上的信息就只有0.5倍能够传递到下一层神经元中,因为被输入到下层神经元中去进行计算的实际值是 0.5 x 0.5x 0.5x。相对的,如果 w 1 w_1 w1是2.5,则会传递2.5倍的 x 1 x_1 x1上的信息。
到此,我们已经了解了线性回归的网络是怎么一回事,它是最简单的回归神经网络,同时也是最简单的神经网络。类似于线性回归这样的神经网络,被称为单层神经网络。
单层神经网络
从直观来看,线性回归的网络结构明明有两层,为什么线性回归被叫做“单层神 经网络”呢?实际上,在描述神经网络的层数的时候,我们不考虑输入层。输入层是每个神经网络都必须存在的一层,任意两个神经网络之间的不同之处就在输入层之后的所有层。所以,我们把输入层之后只有一层的神经网络称为单层神经网络。
#首先使用numpy来创建数据
import numpy as np
X = np.array([[0,0],[1,0],[0,1],[1,1]])
z_reg = np.array([-0.2, -0.05, -0.05, 0.1])
X
X.shape
z_reg
#定义实现简单线性回归的函数
def LinearR(x1,x2):w1, w2, b = 0.15, 0.15,-0.2 #给定一组系数w和bz = x1*w1 + x2*w2 + b #z是系数*特征后加和的结果return z
LinearR(X[:,0],X[:,1])
可以看到,只要能够给到适合的w和b,回归神经网络其实非常容易实现。从这样的一个简单回归神经网络,我们很容易就可以把它推广到分类模型上。
1.2 二分类单层神经网络:sigmoid与阶跃函数
-
sigmoid函数
在过去我们学习逻辑回归时,我们了解到sigmoid函数可以帮助我们将线性回归连续型的结果转化为0-1之间的概率值,从而帮助我们将回归类算法转变为分类算法逻辑回归。对于神经网络来说我们也可以使用相同的方法。首先先来复习一下Sigmoid函数的的公式和性质:Sigmoid函数是一个 S S S型的函数,当自变量 z z z趋近正无穷时,因变量 g ( z ) g(z) g(z)趋近于 1 1 1, 而当 z z z趋近负无穷时, g ( z ) g(z) g(z)趋近于 0 0 0,因此它能够将任何实数映射到 ( 0 , 1 ) (0,1) (0,1)区间,使其可用于将任意值函数转换为更适合二分类的函数。通常来说,自变量往往是回归类算法(如线性回归)的结果。将回归类算法的连续型数值压缩到 ( 0 , 1 ) (0,1) (0,1)之间后,我们使用阈值 0.5 0.5 0.5来将其转化为分类。即当 g ( z ) g(z) g(z)大于0.5时,我们认为样本 z i z_i zi对应的分类结果为 1 1 1类,反之则为 0 0 0类。
g ( z ) = 1 1 + e − z g(z) = \frac{1}{1+ e^{-z}} g(z)=1+e−z1

来看下面这组数据。很容易注意到,这组数据和上面的回归数据的特征 ( x 1 , x 2 ) (x_1,x_2) (x1,x2)是完全一致的,只不过标签 y y y由连续型结果转变为了分类型。这一组分类的规律是这样的:当两个特征都为 1 1 1的时候标签就为 1 1 1,否则标签就为 0 0 0。这一组特殊的数据被我们称之为“与门”(AND GATE),这里的“与”正是表示“特征一与特征二都是 1 1 1”的含义。
#重新定义数据中的标签
y_and = [0,0,0,1]
#根据sigmoid公式定义sigmoid函数
def sigmoid(z): return 1/(1 + np.exp(-z))
def AND_sigmoid(x1,x2): w1, w2, b = 0.15, 0.15,-0.2 #给定的系数w和b不变 z = x1*w1 + x2*w2 + b o = sigmoid(z) #使用sigmoid函数将回归结果转换到(0,1)之间 y = [int(x) for x in o >= 0.5] #根据阈值0.5,将(0,1)之间的概率转变 为分类0和1 return o, y #o:sigmoid函数返回的概率结果
#y:对概率结果按阈值进行划分后,形成的0和1,也就是分类标签
o, y_sigm = AND_sigmoid(X[:,0],X[:,1])
y_sigm == y_and
- sign函数
表达式:
g ( z ) = y = { 1 i f z > 0 0 i f z = = 0 − 1 i f z < 0 g(z) = y = \left\{\begin{matrix} 1 & if z>0\\ 0 &if z==0\\ -1 &if z<0 \end{matrix}\right. g(z)=y=⎩ ⎨ ⎧10−1ifz>0ifz==0ifz<0

由于函数的取值是间断的,符号函数也被称为“阶跃函数”,表示在 0 0 0的两端,函数的结果 y y y是从 − 1 -1 −1直接阶跃到了 1 1 1。在这里,我们使用 y y y而不是 g ( z ) g(z) g(z)来表示输出的结果,是因为输出结果直接是 0 0 0、 1 1 1、 − 1 -1 −1这样的类别。对于sigmoid函数而言, g ( z ) g(z) g(z)返回的是 0 1 0~1 0 1之间的概率值,如果我们希望获取最终预测出的类别,还需要将概率转变成 0 0 0或 1 1 1这样的数字才可以。但符号函数可以直接返回类别,因此我们可以认为符号函数输出的结果就是最终的预测结果 y y y。在二分类中,符号函数也可以忽略中间 z = = 0 z==0 z==0的时 候,直接分为 0 0 0和 1 1 1两类,用如下式子表示:
y = { 1 i f z > 0 − 1 i f z ≤ 0 ∵ z = w 1 x 1 + w 2 x 2 + b ∴ y = { 1 i f w 1 x 1 + w 2 x 2 + b > 0 − 1 i f w 1 x 1 + w 2 x 2 + b ≤ 0 ∴ y = { 1 i f w 1 x 1 + w 2 x 2 > − b − 1 i f w 1 x 1 + w 2 x 2 ≤ − b y = \left\{\begin{matrix} 1 & if z>0\\ -1 &if z\le 0\\ \end{matrix}\right. \\ \because z = w_1x_1 + w_2x_2 +b \\ \therefore y =\left\{\begin{matrix} 1 & if w_1x_1 + w_2x_2 +b >0\\ -1 &if w_1x_1 + w_2x_2 +b \le 0\\ \end{matrix}\right. \\ \therefore y =\left\{\begin{matrix} 1 & if w_1x_1 + w_2x_2 >-b\\ -1 &if w_1x_1 + w_2x_2 \le -b\\ \end{matrix}\right. y={1−1ifz>0ifz≤0∵z=w1x1+w2x2+b∴y={1−1ifw1x1+w2x2+b>0ifw1x1+w2x2+b≤0∴y={1−1ifw1x1+w2x2>−bifw1x1+w2x2≤−b
此时, − b -b −b就是一个阈值,我们可以使用任意字母来替代它,比较常见的是字母 θ \theta θ。当然,不把它当做阈值,依然保留 w 1 x 1 + w 2 x 2 + b w_1x_1 + w_2x_2 +b w1x1+w2x2+b与0进行比较的关系也没有任何问题。和sigmoid一样,我们也可以使用阶跃函数来处理”与门“的数据:
def AND(x1,x2): w1, w2, b = 0.15, 0.15, -0.23 #和sigmoid相似的w和b z = x1*w1 + x2*w2 + b y = [int(x) for x in z >= 0] return y AND(X[:,0],X[:,1]) y_and
阶跃函数和sigmoid都可以完成二分类的任务。在神经网络的二分类中, g ( z ) g(z) g(z)几乎默认是sigmoid函数,少用阶跃函数,这是由神经网络的解法决定的.
1.3 多分类单层神经网络:softmax回归
在了解二分类后,我们可以继续将神经网络推广到多分类。逻辑回归通过Many-vs-Many(多对多)和Onevs-Rest(一对多)模式来进行多分类。其中,OvR是指将多个标签类别中的一类作为类别 1 1 1,其他所有类别作为类别 0 0 0,分别建立多个二分类模型,综合得出多分类结果的方法。MvM是指把好几个标签类作为 1 1 1,剩下的几个标签类别作为 0 0 0,同样分别建立多个二分类模型来得出多分类结果的方法。这两种方法非常有效,尤其是在逻辑回归做多分类的问题上能够解决很多问题,但是对于神经网络却不奏效。理由非常简单:
-
- 逻辑回归是一个单层神经网络,计算非常快速,在使用OvR和MvM这样需要同时建立多个模型的方法时,运算速度不会成为太大的问题。但真实使用的神经网络往往是一个庞大的算法,建立一个模型就会耗费很多时间,因此必须建立很多个模型来求解的方法对神经网络来说就不够高效。
-
- 我们有更好的方法来解决这个问题,那就是softmax回归。
Softmax函数是深度学习基础中的基础,它是神经网络进行多分类时,默认放在输出层中处理数据的函数。假设现在神经网络是用于三分类数据,且三个分类分别是苹果,柠檬和百香果,序号则分别是分类 1、分类2和分类3。则使用softmax函数的神经网络的模型会如下所示:

与二分类一样,我们从网络左侧输入特征,从右侧输出概率,且概率是通过线性回归的结果 z z z外嵌套softmax函数来进行计算。在二分类时,输出层只有一个神经元,只输出样本对于正类别的概率(通常是标签为 1 1 1的概率),而softmax的输出层有三个神经元,分别输出该样本的真实标签是苹果、柠檬或百香果的概率。在多分类中,神经元的个数与标签类别的个数是一致的,如果是十分类,在输出层上就会存在十个神经元,分别输出十个不同的概率。此时,样本的预测标签就是所有输出的概率 σ 1 \sigma_1 σ1, σ 2 \sigma_2 σ2, σ 3 \sigma_3 σ3中最大的概率对应的标签类别。
那每个概率是如何计算出来的呢?来看Softmax函数的公式:
σ k = S o f t m a x ( z k ) = e z k ∑ K e z \sigma_k = Softmax(z_k) = \frac{e^{z_k}}{\sum^K e^z} σk=Softmax(zk)=∑Kezezk
其中 e e e为自然常数(约为2.71828), z z z与sigmoid函数中的一样,表示回归类算法(如线性回归)的结果。 K K K表示该数据的标签中总共有 K K K个标签类别,如三分类时 K = 3 K=3 K=3 ,四分类时 K = 4 K=4 K=4 。 k k k表示标签类别 k k k类。很容易可以看出,Softmax函数的分子是多分类状况下某一个标签类别的回归结果的指数函数,分母是多分类状况下所有标签类别的回归结果的指数函数之和,因此Softmax函数的结果代表了样本的结果为类别 k k k的概率。
举个例子,当我们有三个分类,分别是苹果,梨,百香果的时候,样本 i i i被分类为百香果的概率 σ 百香果 \sigma_{百香果} σ百香果为:
σ 百香果 = σ 百香果 σ 苹果 + σ 梨 + σ 百香果 \sigma_{百香果} = \frac{\sigma_{百香果}}{\sigma_{苹果}+\sigma_{梨}+\sigma_{百香果}} σ百香果=σ苹果+σ梨+σ百香果σ百香果
相关文章:

深度学习-神经网络原理
文章目录 神经网络原理1.单层神经网络1.1 回归单层神经网络:线性回归1.2 二分类单层神经网络:sigmoid与阶跃函数 1.3 多分类单层神经网络:softmax回归 神经网络原理 人工神经网络(Artificial Neural Network,ANN&…...

Chat GPT:智能对话的下一步
Chat GPT:智能对话的下一步 介绍 Chat GPT(Generative Pre-trained Transformer)是一种基于Transformer架构的强大对话模型,可以产生自然流畅的回答,并实现人机对话的感觉。本文将探讨Chat GPT在智能对话领域的影响和…...
[数据集][目标检测]鸡蛋破蛋数据集VOC+YOLO格式792张2类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):792 标注数量(xml文件个数):792 标注数量(txt文件个数):792 标注类别…...

RabbitMQ实战学习
RabbitMQ实战学习 文章目录 RabbitMQ实战学习RabbitMQ常用资料1、安装教程2、使用安装包3、常用命令4、验证访问5、代码示例 一、RabbitMQ基本概念1.1. MQ概述1.2 MQ 的优势和劣势1.3 MQ 的优势1. 应用解耦2. 异步提速3. 削峰填谷 1.4 MQ 的劣势1.5 RabbitMQ 基础架构1.6 JMS 二…...
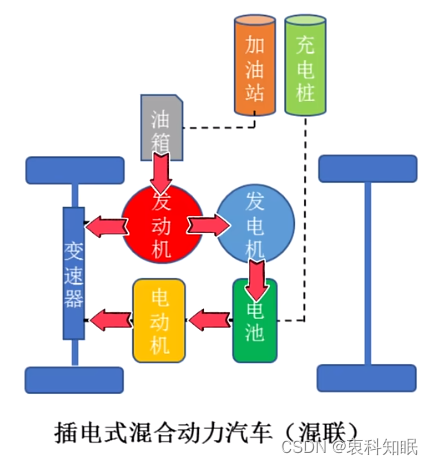
插混、油混、增程式、轻混、强混,啥区别
这里写自定义目录标题 随着我国新能源汽车的大力推进,电车可以说是世界未来的主流,只不过现在是处在一个过渡时代 这是个好时代,因为我们见证并体验着历史过渡的细节 这是个不好的时代,因为我们可能只是未来新新人类的试验品 帮他…...
优化补充)
React 模态框的设计(八)优化补充
在之前的弹窗的设计中,有两处地方现在做一点小小的优化,就是把_Draggable.jsx中的 onPointerEnter 事件 用 useLayoutEffect来规换,效果更佳,同样的,在_ModelContainer.jsx中也是一样。如下所示: _Draggabl…...
:深度学习相关概念(查看检索时看到))
知识积累(三):深度学习相关概念(查看检索时看到)
文章目录 1. 知识蒸馏2. 可微搜索索引(DSI)参考资料 在找论文时,发现的相关概念。 1. 知识蒸馏 知识蒸馏(knowledge distillation)是模型压缩的一种常用的方法,不同于模型压缩中的剪枝和量化,知…...

计算机专业必看的几部电影
目录 编辑 1. 《第九区》(District 9,2009) 2. 《谍影重重》(The Bourne Identity,2002) 3. 《源代码》(Source Code,2011) 4. 《她》(Her,…...

工业人工智能需要注意的10件事
我们无法逃避人工智能这个风口,宣传人工智能软件的广告铺天盖地,似乎每个供应商都在推出最新的工具包,每天都有关于 ChatGPT、Bard 等新用例的文章。似乎全世界都在说:你现在需要人工智能! 人工智能确实正在成为自动化…...

软考-系统集成项目管理中级-信息系统建设与设计
本章重点考点 1.信息系统的生命周期 信息系统建设的内容主要包括设备采购、系统集成、软件开发和运维服务等。信息系统的生命周期可以分为四个阶段:立项、开发、运维和消亡。 2.信息系统开发方法 信息系统常用的开发方法有结构化方法、原型法、面向对象方法等 1)结构化方法 …...
)
C++从零开始的打怪升级之路(day39)
这是关于一个普通双非本科大一学生的C的学习记录贴 在此前,我学了一点点C语言还有简单的数据结构,如果有小伙伴想和我一起学习的,可以私信我交流分享学习资料 那么开启正题 今天分享的是关于模板的知识点 1.非类型模板参数 模板参数分为…...

Java面试题之并发
并发 1.并发编程的优缺点?2.并发编程三要素?3.什么叫指令重排?4.如何避免指令重排?5.并发?并行?串行?6.线程和进程的概念和区别?7.什么是上下文切换?8.守护线程和用户线程的定义?9.什么是线程死锁?10.形成死锁的四个条件?11.怎么避免死锁?12.创建线程的四种方式?…...

Python GUI自动化定位代码参考
一、pyautogui原始逻辑 import pyautogui # 获取指定图片在屏幕上的位置 image_path path/to/image.png target_position pyautogui.locateCenterOnScreen(image_path) if target_position is not None: # 获取偏移量 offset_x 10 offset_y 10 # 计算实际点…...

11.网络游戏逆向分析与漏洞攻防-游戏网络架构逆向分析-接管游戏接收网络数据包的操作
内容参考于:易道云信息技术研究院VIP课 上一个内容:接管游戏发送数据的操作 码云地址(master 分支):https://gitee.com/dye_your_fingers/titan 码云版本号:8256eb53e8c16281bc1a29cb8d26d352bb5bbf4c 代…...
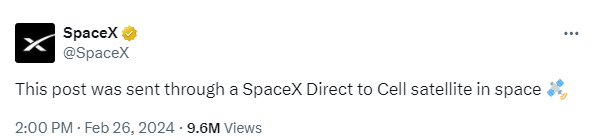
特斯拉一面算法原题
来自太空的 X 帖子 埃隆马斯克(Elon Musk)旗下太空探索技术公司 SpaceX 于 2 月 26 号,从太空往社交平台 X(前身为推特,已被马斯克全资收购并改名)发布帖子。 这是 SpaceX 官号首次通过星链来发送 X 帖子&a…...

【Leetcode每日一题】二分查找 - 山脉数组的峰顶索引(难度⭐⭐)(23)
1. 题目解析 Leetcode链接:852. 山脉数组的峰顶索引 这个问题的理解其实相当简单,只需看一下示例,基本就能明白其含义了。 核心在于找到题目中所说的峰值所在的下标并返回他们的下标即可。 2. 算法原理 峰顶及两侧数据特点分析 峰顶数据…...
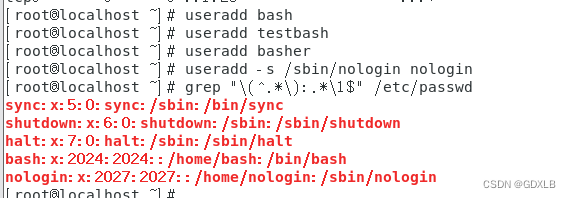
Linux添加用户分组练习
一、复制/etc/skel目录为/home/tuser1(/home/tuser1及其内部文件的属组和其它用户均没有任何访问权限)。 cp -a /etc/skel /home/tuser1 chown -R tuser1:tuser1 /home/tuser1 chmod -R 700 /home/tuser1 二、编辑/etc/group文件,添加组h…...

云快充充电桩系统设计书
充电桩系统设计书 一、系统设计概述 随着新能源汽车市场的快速发展,充电桩作为电动汽车的重要配套设施,其市场需求日益增长。本系统旨在提供一套稳定、高效、易用的充电桩解决方案,以满足市场上新能源充电桩的主流需求。通过实现云快充V1.6协…...

oracle DG 原理
在Oracle中,什么是DG?DG有哪些优缺点? DG(Data Guard,数据卫士)不是一个备份恢复的工具,然而,DG却拥有备份的功能,在物理DG下它可以和主库一模一样,但是它存…...

MySQL篇—持久化和非持久化统计信息介绍(第一篇,总共三篇)
☘️博主介绍☘️: ✨又是一天没白过,我是奈斯,DBA一名✨ ✌✌️擅长Oracle、MySQL、SQLserver、Linux,也在积极的扩展IT方向的其他知识面✌✌️ ❣️❣️❣️大佬们都喜欢静静的看文章,并且也会默默的点赞收藏加关注❣…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...
