算法复习之二分【备战蓝桥杯】
二分模板一共有两个,分别适用于不同情况。
算法思路:假设目标值在闭区间[l, r]中, 每次将区间长度缩小一半,当l = r时,我们就找到了目标值。
版本一
当我们将区间[l, r]划分成[l, mid]和[mid + 1, r]时,其更新操作是r = mid或者l = mid + 1;计算mid时不需要加1。
int bsearch_1(int l, int r)
{while (l < r){int mid = l + r >> 1;if (check(mid)) r = mid;else l = mid + 1;}return l;
}
版本二
当我们将区间[l, r]划分成[l, mid - 1]和[mid, r]时,其更新操作是r = mid - 1或者l = mid;此时为了防止死循环,计算mid时需要加1。
int bsearch_2(int l, int r)
{while (l < r){int mid = l + r + 1 >> 1;if (check(mid)) l = mid;else r = mid - 1;}return l;
}
总结
假设有一个总区间,经由我们的 check 函数判断后,可分成两部分,
这边以o作 true,…作 false 示意较好识别
如果我们的目标是下面这个v,那麽就必须使用模板 1
…vooooooooo
假设经由 check 划分后,整个区间的属性与目标v如下,则我们必须使用模板 2
oooooooov…
所以下次可以观察 check 属性再与模板1 or 2 互相搭配就不会写错啦
练习题
503. 借教室
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;typedef long long LL;
const int N = 1000010;
int n, m;
int w[N];
int d[N], l[N], r[N];
LL b[N];bool check(int mid)
{memset(b, 0, sizeof b);for (int i = 1; i <= mid; i ++ ) {b[l[i]] += d[i];b[r[i] + 1] -= d[i];}for (int i = 1; i <= n; i ++ ) {b[i] += b[i - 1];if (b[i] > w[i]) return false;}return true;
}int main()
{scanf("%d%d", &n, &m);for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);for (int i = 1; i <= m; i ++ ) scanf("%d%d%d", &d[i], &l[i], &r[i]);int l = 0, r = m;while(l < r){int mid = l + r + 1>> 1;if (check(mid)) l = mid;else r = mid - 1;}if (r == m) printf("0\n");else printf("-1\n%d", r + 1);return 0;
}作者:大四萌新.
链接:https://www.acwing.com/activity/content/code/content/7899026/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
1227. 分巧克力
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 1e5 + 10;int n, k;
int h[N], w[N];bool check(int mid)
{int sum = 0;for (int i = 0; i < n; i ++ ) {sum += (h[i] / mid) * (w[i] / mid);if (sum >= k) return true;}return false;
}int bsearch()
{int l = 1, r = 1e5 + 10;while (l < r) {int mid = l + r + 1 >> 1;if (check(mid)) l = mid;else r = mid - 1;}
}int main()
{scanf("%d%d", &n, &k);for (int i = 0; i < n; i ++ ) scanf("%d%d", &h[i], &w[i]);printf("%d", bsearch());return 0;
}作者:大四萌新.
链接:https://www.acwing.com/activity/content/code/content/7878482/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
4956. 冶炼金属
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 10010;
int n;
int a[N], b[N];bool check_1(int mid)
{// 找最小的 那么其他部分都得满足小于等于b[i]for (int i = 0; i < n; i ++ ) if (a[i] / mid > b[i]) return false;return true;
}bool check_2(int mid)
{// 找最大得 那么其他部分都得满足大于等于b[i]for (int i = 0; i < n; i ++ ) if (a[i] / mid < b[i]) return false;return true;
}int main()
{scanf("%d", &n);for (int i = 0; i < n; i ++ ) scanf("%d%d", &a[i], &b[i]);int l = 1, r = 1e9 + 1;while (l < r) {int mid = l + r >> 1;if (check_1(mid)) r = mid;else l = mid + 1;}printf("%d ", l);r = 1e9 + 1;while (l < r){int mid = l + r + 1 >> 1;if (check_2(mid)) l = mid;else r = mid - 1;}printf("%d", l);return 0;
}作者:大四萌新.
链接:https://www.acwing.com/activity/content/code/content/7899986/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
相关文章:

算法复习之二分【备战蓝桥杯】
二分模板一共有两个,分别适用于不同情况。 算法思路:假设目标值在闭区间[l, r]中, 每次将区间长度缩小一半,当l r时,我们就找到了目标值。 版本一 当我们将区间[l, r]划分成[l, mid]和[mid 1, r]时,其更…...
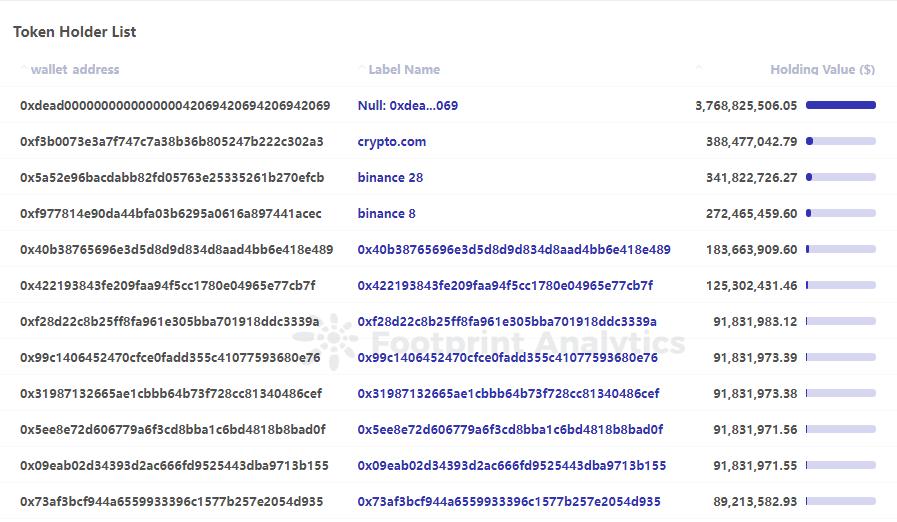
如何做代币分析:以 SHIB 币为例
作者:lesleyfootprint.network 编译:cicifootprint.network 数据源:SHIB Token Dashboard (仅包括以太坊数据) 在加密货币和数字资产领域,代币分析起着至关重要的作用。代币分析指的是深入研究与代币相关…...
Springboot+vue的考勤管理系统(有报告)。Javaee项目,springboot vue前后端分离项目。
演示视频: Springbootvue的考勤管理系统(有报告)。Javaee项目,springboot vue前后端分离项目。 项目介绍: 采用M(model)V(view)C(controller)三层…...
https://htmlunit.sourceforge.io/
https://htmlunit.sourceforge.io/ 爬虫 HtmlUnit – Welcome to HtmlUnit HtmlUnit 3.11.0 API https://mvnrepository.com/artifact/net.sourceforge.htmlunit/htmlunit/2.70.0 https://s01.oss.sonatype.org/service/local/repositories/releases/content/org/htmlunit…...
)
回文链表(leetcode)
我自己第一个写的代码: bool isPalindrome(struct ListNode* head){struct ListNode* tail NULL;struct ListNode* pos NULL;if( head->next NULL){return true;}while( 1 ){if( head->next NULL || (head->next->next NULL && head->…...
技术名词表(一))
大语言模型(LLM)技术名词表(一)
LLMs on a Phone:指在手机设备上运行的大型语言模型。 Scalable Personal AI:指用户可以在个人设备上对AI模型进行微调的技术。 Responsible Release:发布AI模型时考虑社会、法律和伦理影响的做法。 Multimodality:AI模型能处理…...

C++ 快速排序快速选择
目录 1、75. 颜色分类 2、912. 排序数组 3、 215. 数组中的第K个最大元素 4、LCR 159. 库存管理 III 1、75. 颜色分类 思路:利用快速排序思路,使用三指针分块进行优化。 [0,left]——小于key[left1,right-1]——等于key[right,nums.size()]——大于k…...
雅马哈伺服器TS-S系列说明具体详情内容可参看PDF目录内容
雅马哈伺服器TS-S系列说明具体详情内容可参看PDF目录内容...
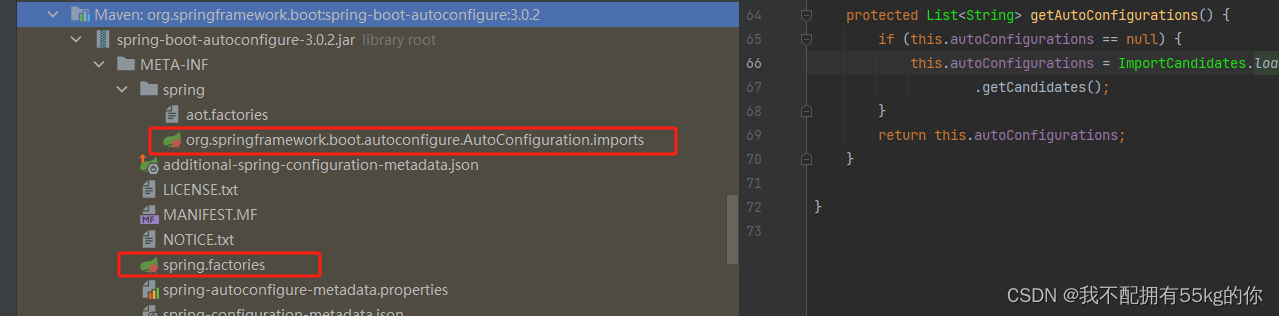
SpringBoot底层原理
SpringBoot底层原理 一 配置优先级 1.配置方式 Springboot中支持三种配置方式,分别为: application.propertiesapplication.ymlapplication.yaml 2.配置优先级 当存在多份配置文件时,配置文件会按照它们的优先级生效。 优先级从高到底…...
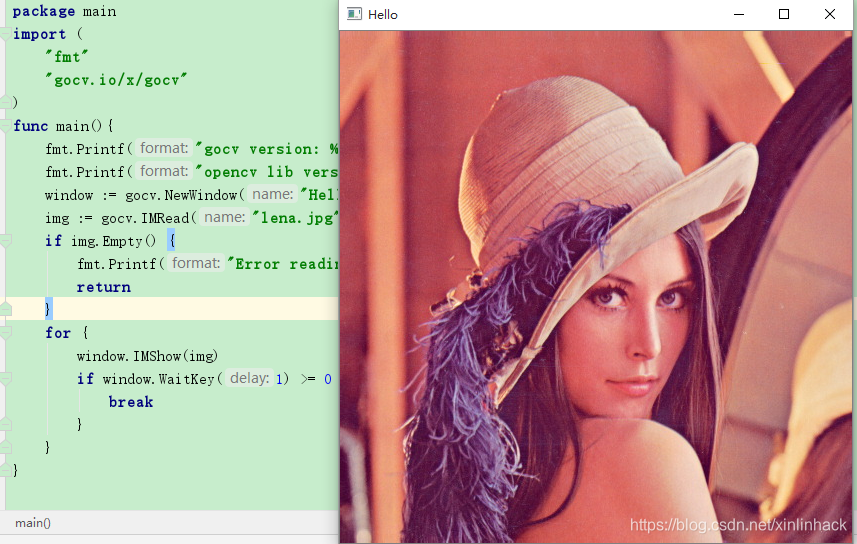
【golang】25、图片操作
用 “github.com/fogleman/gg” 可以画线, 框 用 “github.com/disintegration/imaging” 可以变换颜色 一、渲染 1.1 框和字 import "github.com/fogleman/gg"func DrawRectangles(inPath string, cRects []ColorTextRect, fnImgNameChange FnImgNameChange) (st…...
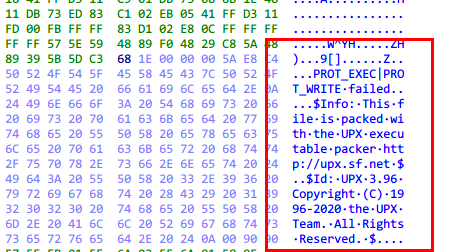
kswapd0挖矿病毒攻击记录
文章目录 一、起因与病毒分析1、起因2、阿里云告警2.1 恶意脚本代码执行12.2 恶意脚本代码执行22.3恶意脚本代码执行32.4 恶意脚本代码执行4 3、病毒简单分析3.1 病毒的初始化3.2 病毒本体执行 4、总结 二、ubuntu自救指南1、病毒清理2、如何防御 一、起因与病毒分析 1、起因 …...

如何使用 takeUntil RxJS 操作符来声明性地管理订阅
简介 Angular 处理取消订阅可观察对象的操作,比如从 HTTP 服务返回的可观察对象或者使用 async 管道时。然而,对于其他情况,管理所有订阅并确保取消长期存在的订阅可能会变得困难。而且,取消大部分订阅的策略也会带来自己的问题。…...
在Centos中用Docker部署oracle-12c
一、介绍 Oracle 12c是Oracle 11g的后续版本。12c代表云计算(Cloud Computing),这是Oracle在该版本中强调的一个关键概念。它具有多租户架构、数据库内存、安全增强、大数据管理和自动化管理等功能。它被广泛应用于企业级应用程序和大型数据…...

JS进阶——高级技巧
版权声明 本文章来源于B站上的某马课程,由本人整理,仅供学习交流使用。如涉及侵权问题,请立即与本人联系,本人将积极配合删除相关内容。感谢理解和支持,本人致力于维护原创作品的权益,共同营造一个尊重知识…...

TG-ADMIN 权限管理系统
项目简介 该项目是一款基于 SpringBoot + Vue2 + Jwt + ElementUi的 RBAC模型管理系统。 主要以自定义拦截器和jwt结合进行权限验证 通过自定义指令实现按钮级别权限,使用经典的RBAC模型 什么是RBAC? 1、RBAC模型概述 RBAC模型(Role-Based Access Control:基于角色的…...
)
十五届蓝桥杯第三期模拟赛题单(C++、java、Python)
备战2024年蓝桥杯 省赛第三期模拟赛题单 备战Python大学A组 第一题 【问题描述】 请问 2023 有多少个约数?即有多少个正整数,使得 2023 是这个正整数的整数倍。 【问题描述】 这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果…...

嵌入式驱动学习第一周——git的使用
前言 本文主要介绍git的使用,包括介绍git,gitee,以及使用gitee创建仓库并托管代码 嵌入式驱动学习专栏将详细记录博主学习驱动的详细过程,未来预计四个月将高强度更新本专栏,喜欢的可以关注本博主并订阅本专栏…...
界面控件DevExpress .NET MAUI v23.2新版亮点 - 拥有全新的彩色主题
DevExpress拥有.NET开发需要的所有平台控件,包含600多个UI控件、报表平台、DevExpress Dashboard eXpressApp 框架、适用于 Visual Studio的CodeRush等一系列辅助工具。屡获大奖的软件开发平台DevExpress 今年第一个重要版本v23.1正式发布,该版本拥有众多…...
的意义)
大语言模型LLM Pro+中Pro+(Prompting)的意义
—— Pro ,即Prompting,构造提示 1.LLM Pro中Pro(Prompting)的意义 Prompting不仅是大语言模型交互和调用的一种高效手段,而且已成为推动模型泛化能力和应用灵活性的关键技术路径,它不仅极大地拓展了模型功…...

React 中,children 属性
在 React 中,children 属性是一个特殊的属性,它允许你将组件作为其他组件的子元素传递。这意味着你可以在组件内部嵌套任何类型的子组件或元素,并且在父组件中通过 props.children 访问它们。这为组件的复用和组合提供了极大的灵活性。 以下…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...
