m位数问题(c++题解)
题目描述
考官只给两个整数n和m(1 <= n <= 8,1<= m <=5),要求选手从1,2,…,n中取出m个数字,组成一个m位整数,统计所有的m位整数中一共有多少个素数。 如n=3,m=2时,符合条件的整数有:11 12 13 21 22 23 31 32 33。 其中素数有:11 13 23 31,一共有4个。
输入格式
一行,两个整数n m,(1 <= n <= 8,1<= m <=5 )。
输出格式
一行,一个整数,表示素数的个数。
样例
样例输入
复制3 2
样例输出
复制4
_____________________________________________________________________________
气死我啦,优化判断素数时没注意把2的情况漏了,90排错排了好久
写作不易,点个赞呗!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
_____________________________________________________________________________
#include <bits/stdc++.h>
using namespace std;
int su(int x){if(x==2)return 0;if(x%2==0||x==1)return 1;int y=sqrt(x);int cnt=0;for(int i=3;i<=y;i+=2)if(x%i==0)return 1; return 0;
}
int a[100005],n,m,ans;
void node(int y,int z){if(z==m){if(su(y)==0)ans++;return;}for(int i=1;i<=n;i++){node(y*10+i,z+1);}
}
int main(){cin>>n>>m;if(n==4&&m==2)cout<<2;else{node(0,0);cout<<ans;}
}相关文章:
)
m位数问题(c++题解)
题目描述 考官只给两个整数n和m(1 < n < 8,1< m <5),要求选手从1,2,…,n中取出m个数字,组成一个m位整数,统计所有的m位整数中一共有多少个素数。 如n3,m2时,符合条件的整数有&…...

洛谷P1331海战
题目背景 在峰会期间,武装部队得处于高度戒备。警察将监视每一条大街,军队将保卫建筑物,领空将布满了 F-2003 飞机。 此外,巡洋船只和舰队将被派去保护海岸线。不幸的是,因为种种原因,国防海军部仅有很少…...

如何利用Flutter来写后端 服务端应用
前言 Flutter是谷歌推出的一款跨平台开发框架,现在属于此领域star最多的框架,其被广泛应用于构建前台界面,但或许很少人知道,他也可以写后端应用。 本文主角 flutter非常著名的getx库推出的get server jonataslaw/get_server:…...
)
数据页和缓存页(BufferPool)
1. 数据页(dataPage) 什么是数据页? 数据页是 MySQL 存储引擎在磁盘和内存之间传输数据的基本单位,默认大小为16KB。 数据页的结构: 表头:储存与页相关的元信息,比如,页号&#…...

LibreOJ 136. 最小瓶颈路 题解 最小生成树 倍增
题目链接:LibreOJ 136. 最小瓶颈路 题目描述: 给定一张无向图,询问两个结点之间的最小瓶颈路。u和v两个结点之间最小瓶颈路指的是u和v的每条路径中经过的最大边权的最小值。 题解: 给出结论:无向图的最小瓶颈路与其最小…...

前端学习第三天-css基础
1. CSS简介 从HTML被发明开始,样式就以各种形式存在。不同的浏览器结合它们各自的样式语言为用户提供页面效果的控制。最初的HTML只包含很少的显示属性。 随着HTML的成长,为了满足页面设计者的要求,HTML添加了很多显示功能。但是随着这些功能…...

各种使用chatgpt prompts技巧
1,利用chatgpt生成照片 1.1,从现在起, 当你想发送一张照片时,请使用 Markdown ,并且 不要有反斜线, 不要用代码块。使用 Unsplash API (https://source.unsplash.com/1280x720/? < PUT YOUR QUERY HERE >)。如果你明白了,请回复“明白” 1.2,开始提问生成指定场景照…...

基于单片机的企业指纹考勤系统设计
摘要: 考勤系统是企业人力资源管理的重要依据,传统的考勤系统不能保证准确性,也存在地域局限,不能满足一些跨区域集团公司的考勤要求。文章以单片机技术以及生物特征识别技术为基础,分析企业单片机智能化指纹考勤系统的设计思路,从硬件设备的选型和配置、软件系统的开发、…...
的常见类介绍)
JUC(java.util.concuurrent)的常见类介绍
Java 并发包(java.util.concurrent,简称 JUC)提供了一系列的工具和框架,用于简化并发编程。以下是 JUC 包中常见类的介绍: Callable: Callable 接口是 Java 提供的一个带返回值的任务接口,类似于…...
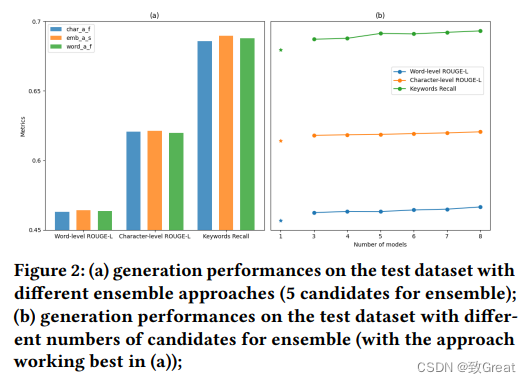
【中科院计算所】WSDM 2024冠军方案:基于大模型进行多文档问答
作者:李一鸣 张兆 中科院计算所 会话式多文档问答旨在根据检索到的文档以及上下文对话来回答特定问题。 在本文中,我们介绍了 WSDM Cup 2024 中“对话式多文档 QA”挑战赛的获胜方法,该方法利用了大型语言模型 (LLM) 卓越的自然语言理解和生…...

Android提供了多种方式来打开特定文件夹中的视频
使用 MediaStore获取指定文件夹的视频,更优化方法: import android.content.ContentResolver; import android.content.ContentValues; import android.content.Context; import android.net.Uri; import android.os.Build; import android.os.Environme…...
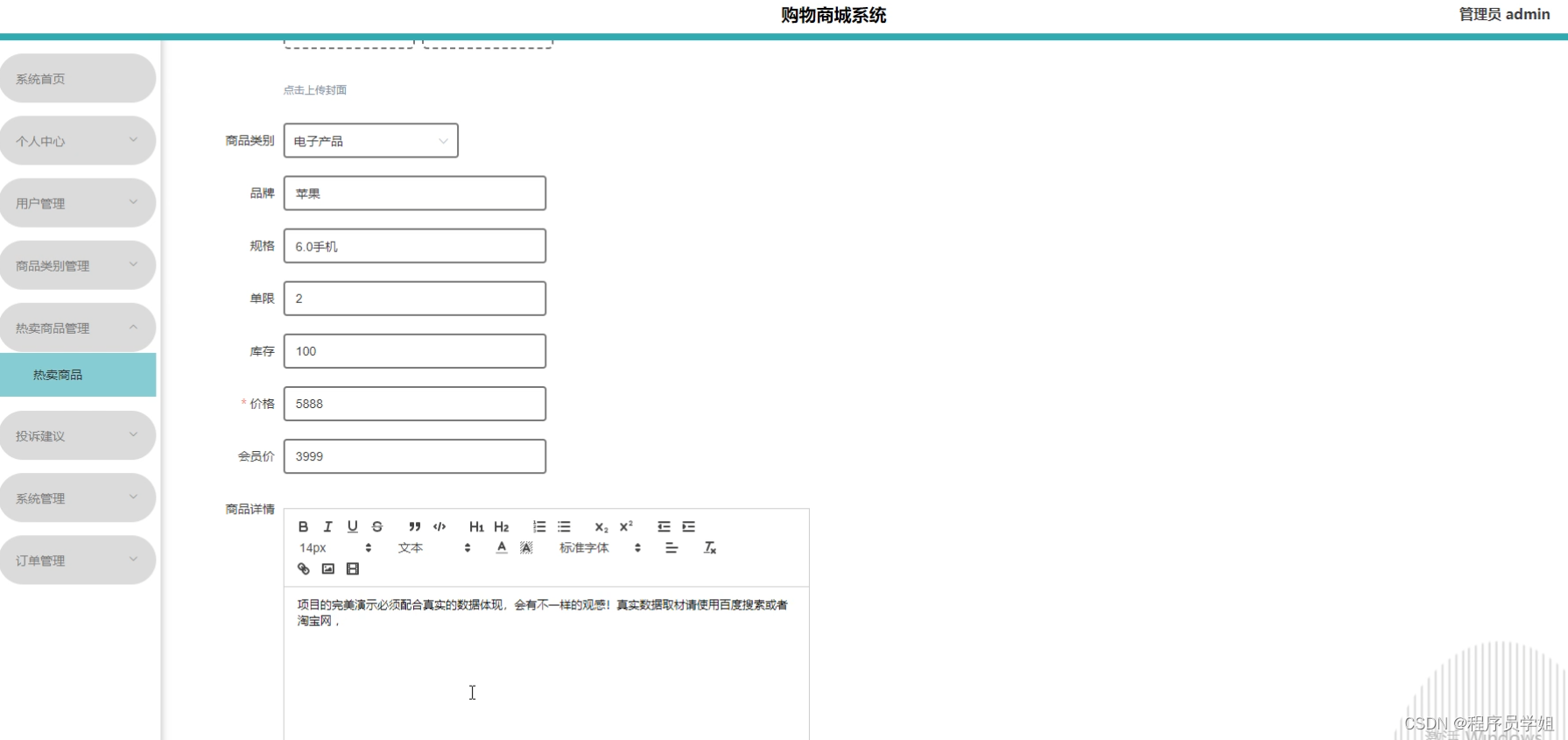
基于django的购物商城系统
摘要 本文介绍了基于Django框架开发的购物商城系统。随着电子商务的兴起,购物商城系统成为了许多企业和个人创业者的首选。Django作为一个高效、稳定且易于扩展的Python web框架,为开发者提供了便捷的开发环境和丰富的功能模块,使得开发购物商…...
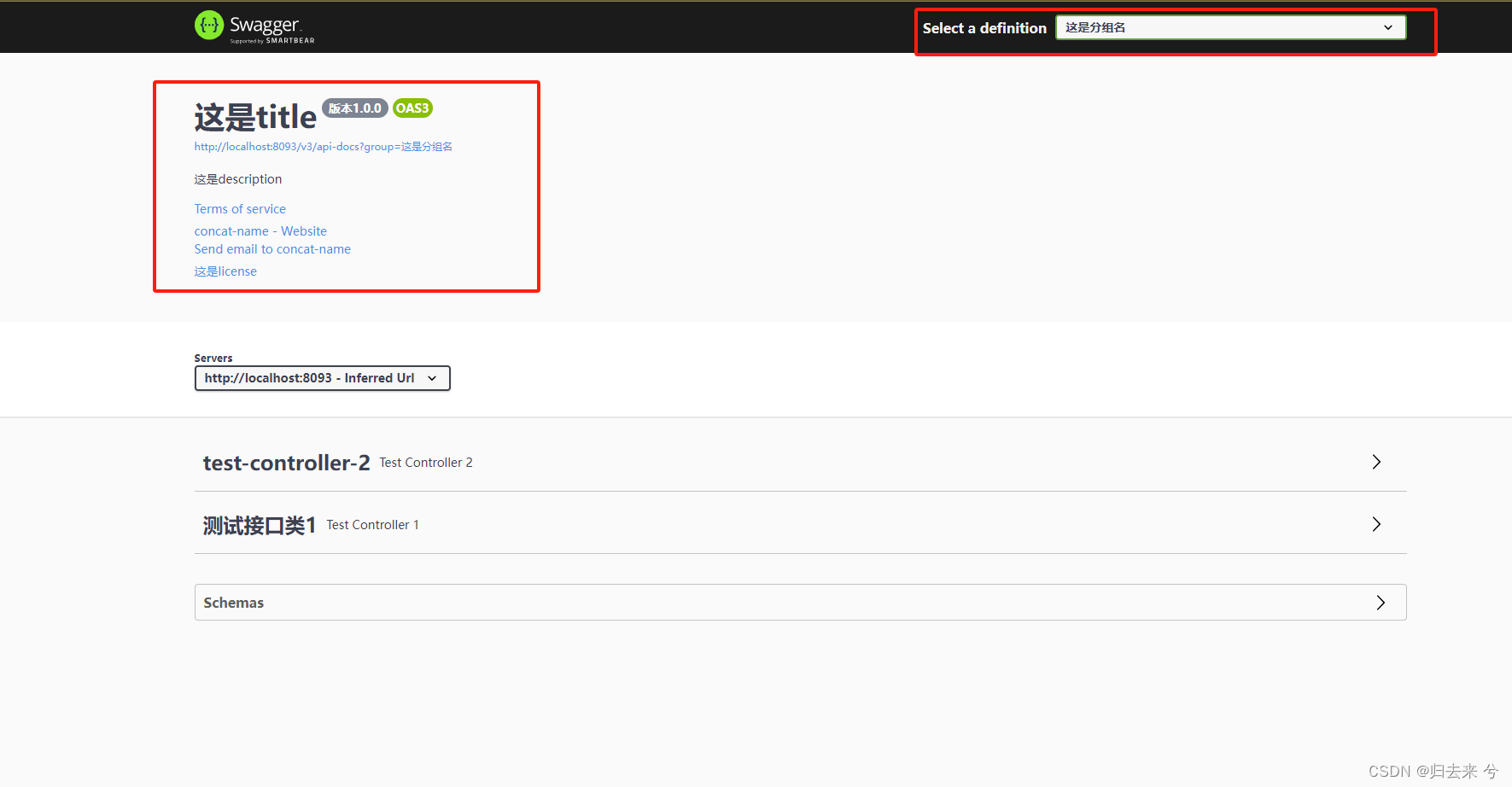
Swagger3 使用详解
Swagger3 使用详解 一、简介1 引入依赖2 开启注解3 增加一个测试接口4 启动服务报错1.5 重新启动6 打开地址:http://localhost:8093/swagger-ui/index.html 二、Swagger的注解1.注解Api和ApiOperation2.注解ApiModel和ApiModelProperty3.注解ApiImplicitParams和Api…...

JVM 第二部分-2(堆,方法区)
4.堆 堆 一个Java程序(main方法)对应一个jvm实例,一个jvm实例只有一个堆空间堆是jvm启动的时候就被创建,大小也确定了。大小可以用参数设置。堆是jvm管理的一块最大的内存空间 核心区域,是垃圾回收的重点区域堆可以位…...
蓝桥杯Java B组历年真题(2013年-2019年)
一、2013年真题 1、世纪末的星期 使用日期类判断就行,这里使用LocalDate,也可以使用Calendar类 答案 2099 使用LocalDate import java.time.LocalDate; import java.time.format.DateTimeFormatter; // 1:无需package // 2: 类名必须Main, 不可修改p…...

你是谁,便会遇见谁
就会进什么样的圈子。努力提升自己,才是提升阶层最可靠的方法。 在人生的舞台上,每一个人都是自己人生的主角。而在这个旅程中,我们会遇见各种各样的人,进入不同的社交圈子。正如一句古训所说:“你是谁,便…...
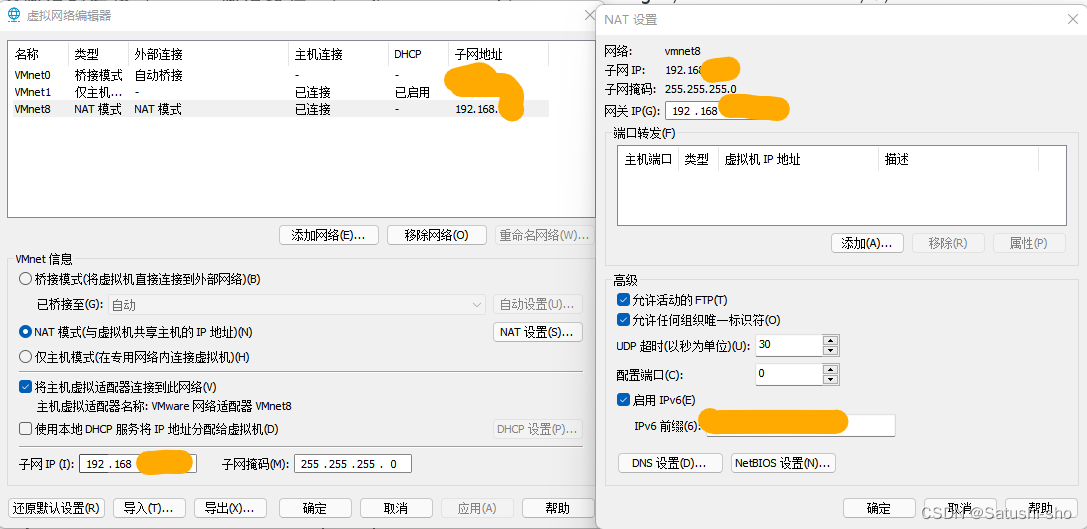
Linux/Centos 部署静态IP,解决无法访问目标主机、Destination Host Unreachable、无法ping通互联网的问题
Linux/Centos 部署IP,解决无法访问目标主机、Destination Host Unreachable、无法ping通互联网的问题 Linux/Centos 部署静态IP查物理机/自身电脑的IP设置VMware上的虚拟网络编辑器设置网卡IP,激活至此就可访问百度了 Linux/Centos 部署静态IP 需要注意…...
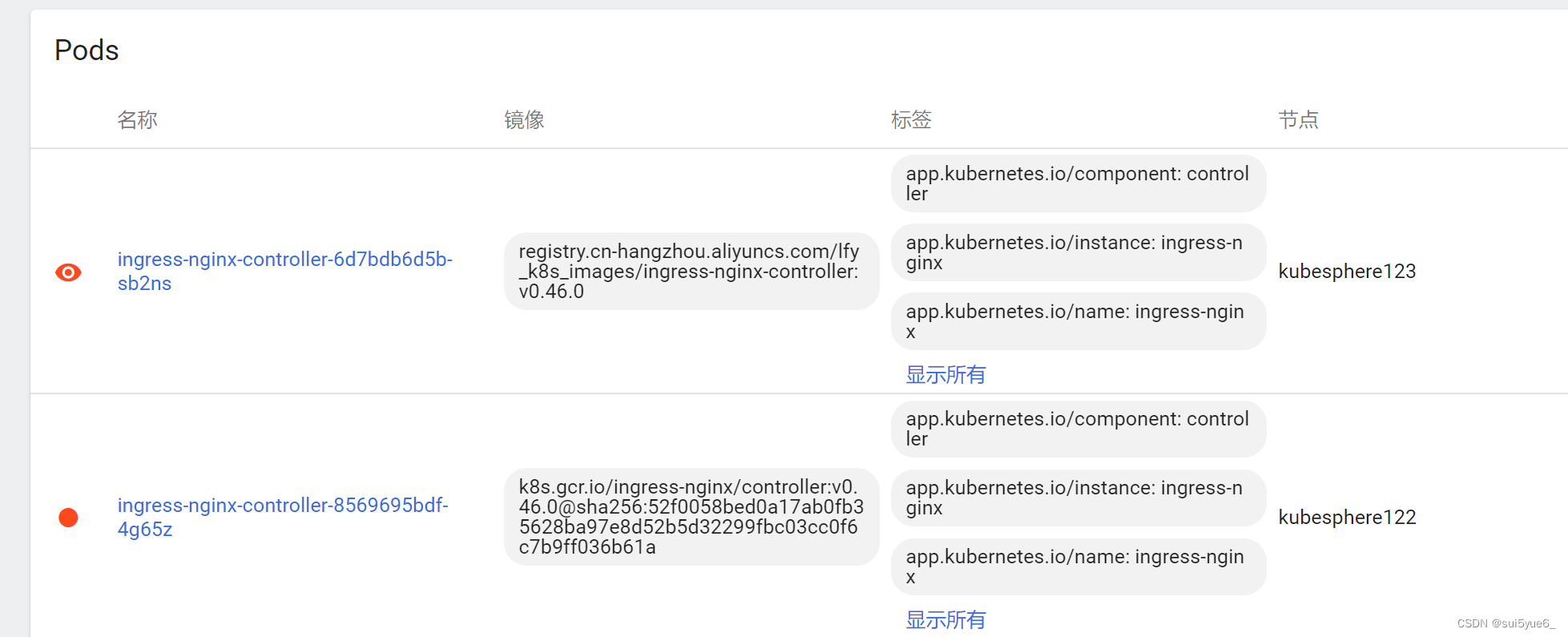
在学习云原生的时候,一直会报错ImagePullBackOff Back-off pulling image
在学习云原生的时候,一直会报错 (见最后几张图) ImagePullBackOff Back-off pulling image 然后我就在像。这个配置的镜像是不是可以自己直接下载,但是好像不怎么搜索得到 然后就在想,这个lfy_k8s_images到底是个啥玩…...

Android Activity跳转详解
在Android应用程序中,Activity之间的跳转是非常常见的操作,通过跳转可以实现不同界面之间的切换和交互。在本篇博客中,我们将介绍Android中Activity跳转的相关知识,包括基本跳转、传递参数、返回数据以及跳转到浏览器、拨号应用和…...

计算机网络(2)-----数据链路层
目录 一.数据链路层的基本概念 二.数据链路层的功能概述 功能一:为网络层提供服务。无确认无连接服务,有确认无连接服务,有确认面向连接服务。 功能二:链路管理,即连接的建立、维持、释放(用于面向连接的服务)。 功能三:组帧 透明传输:…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...
