吴恩达机器学习全课程笔记第四篇
目录
前言
P61-P68
激活函数
Softmax算法
P69-P73
Adam算法
更多类型的层
模型评估
P74-P79
偏差和方差
建立表现基准
学习曲线
偏差和方差与神经网络
前言
这是吴恩达机器学习笔记的第四篇,第三篇笔记请见:
吴恩达机器学习全课程笔记第三篇
完整的课程链接如下:
吴恩达机器学习教程(bilibili)
推荐网站:
scikit-learn中文社区
吴恩达机器学习资料(github)
P61-P68
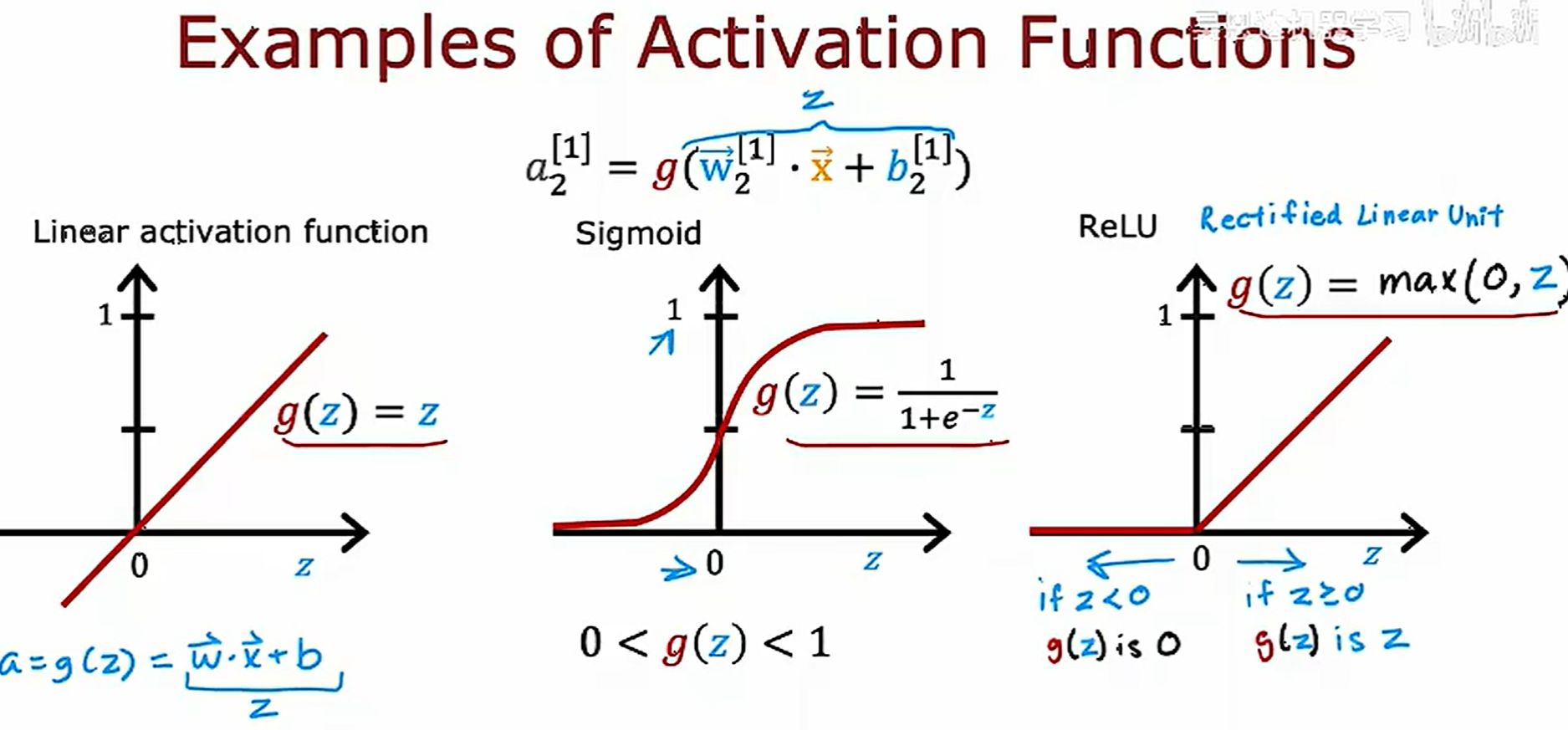
激活函数
激活函数(Activation Function)是一种添加到人工神经网络中的函数,旨在帮助网络学习数据中的复杂模式。在神经元中,输入的input经过一系列加权求和后作用于另一个函数,这个函数就是这里的激活函数

sigmoid的替代品-ReLU
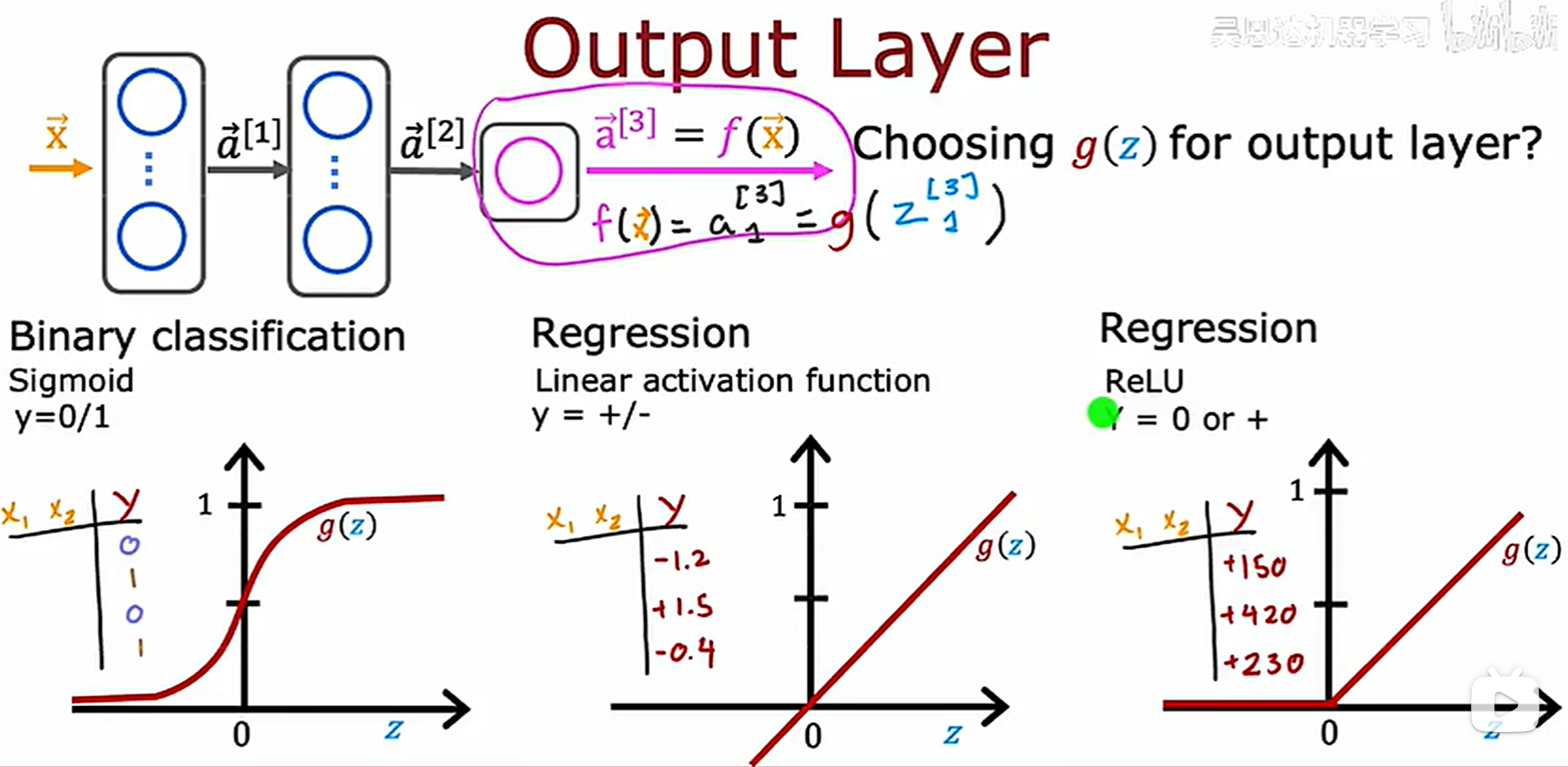
对于二进制分类问题,使用sigmoid激活函数或许是最好的选择,输出的刚好是标签为1的概率
在解决一个回归问题的时候,可以选择不同的激活函数,对于股票问题,可以选择普通的线性激活函数,对于其它的结果不为负的问题,可以选用ReLU
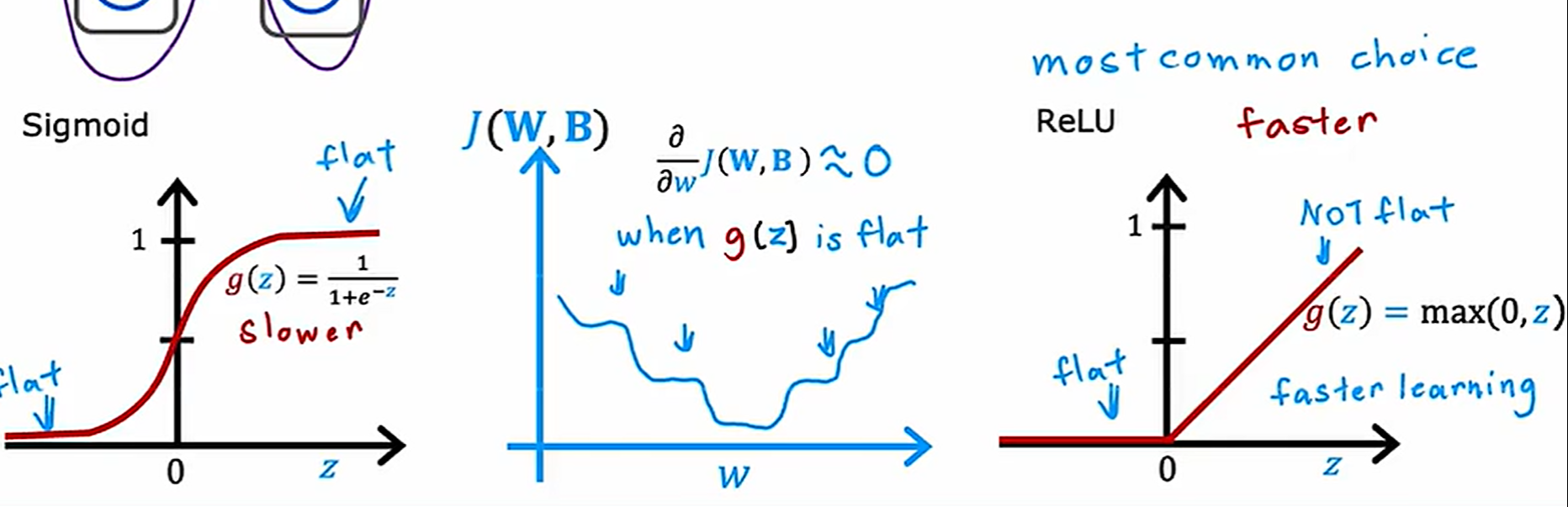
使用relu激活函数不仅本身计算快,而且可以使神经网络梯度下降得快一些
结合之前的神经网络例子,给出tensorflow代码:

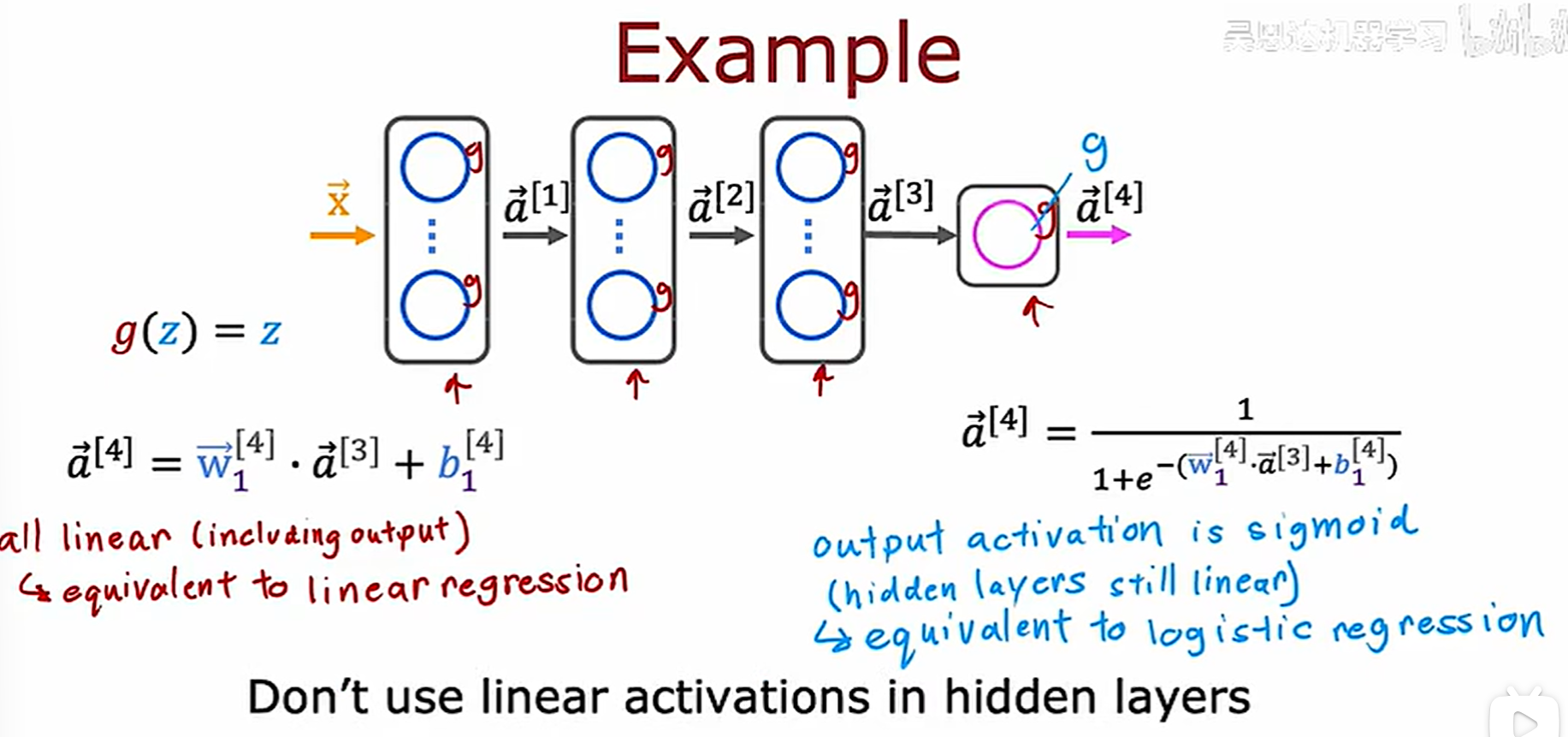
在神经网络的隐藏层中需要使用非线性激活函数, 这是因为需要在网络中引入非线性来学习复杂的模式。 如果没有非线性激活函数,具有许多隐藏层的神经网络将成为一个巨大的线性回归模型,这对于从现实世界数据中学习复杂模式毫无用处。
如果不用激活函数,每一层输出都是上层输入的线性函数,无论神经网络有多少层,输出都是输入的线性组合,即W = W3*[W2*(W1*x)]。
如果隐藏层不使用激活函数,仅在输出层使用sigmoid函数,那么效果仅仅和标准Logistic回归一样
Softmax算法
多分类问题:

softmax回归算法是logistics回归的推广

下面展示softmax的成本函数
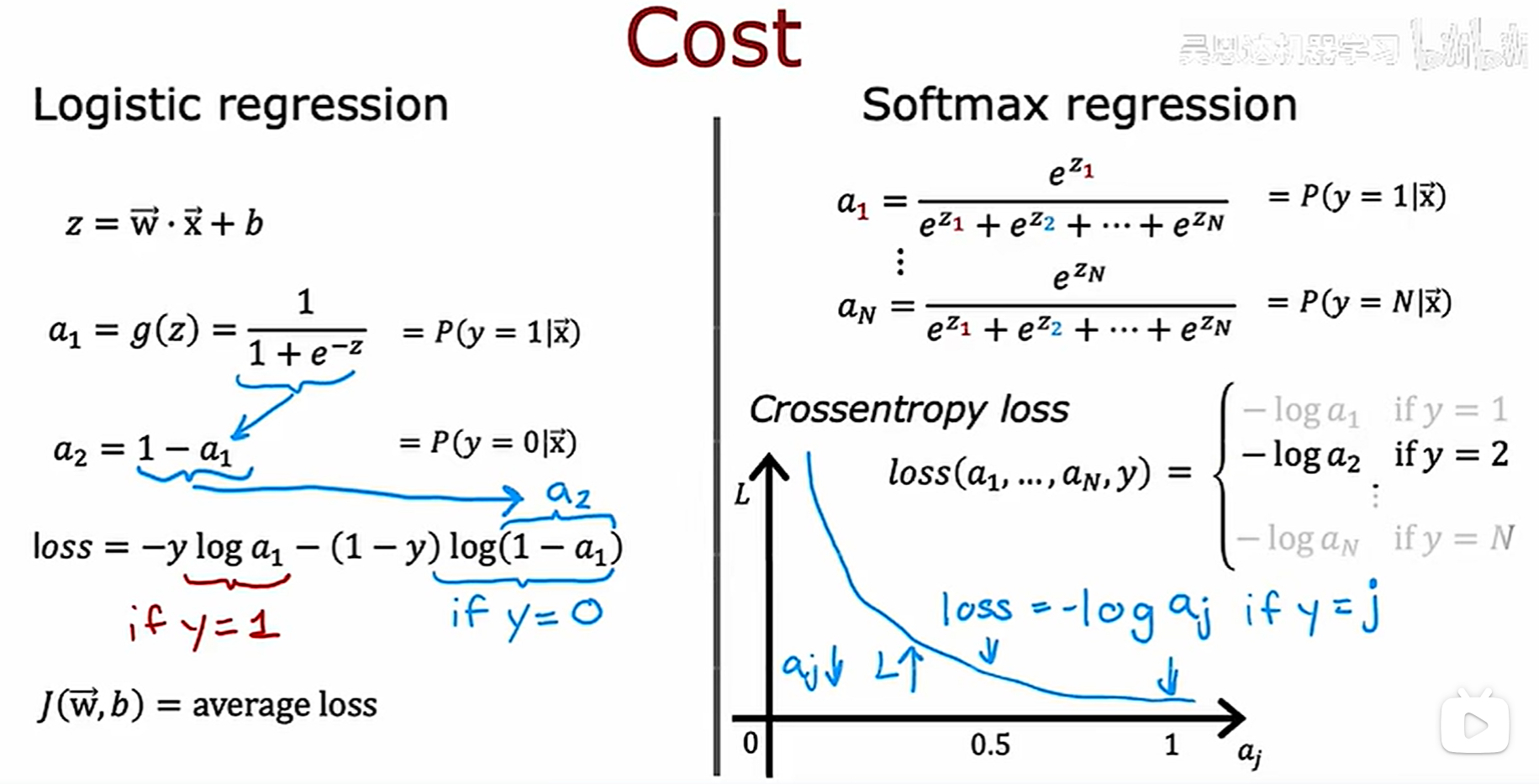
softmax作为输出的激活函数可以使每个激活值都依赖于z的所有值,还是拿之前那个识别手写数字的例子来看
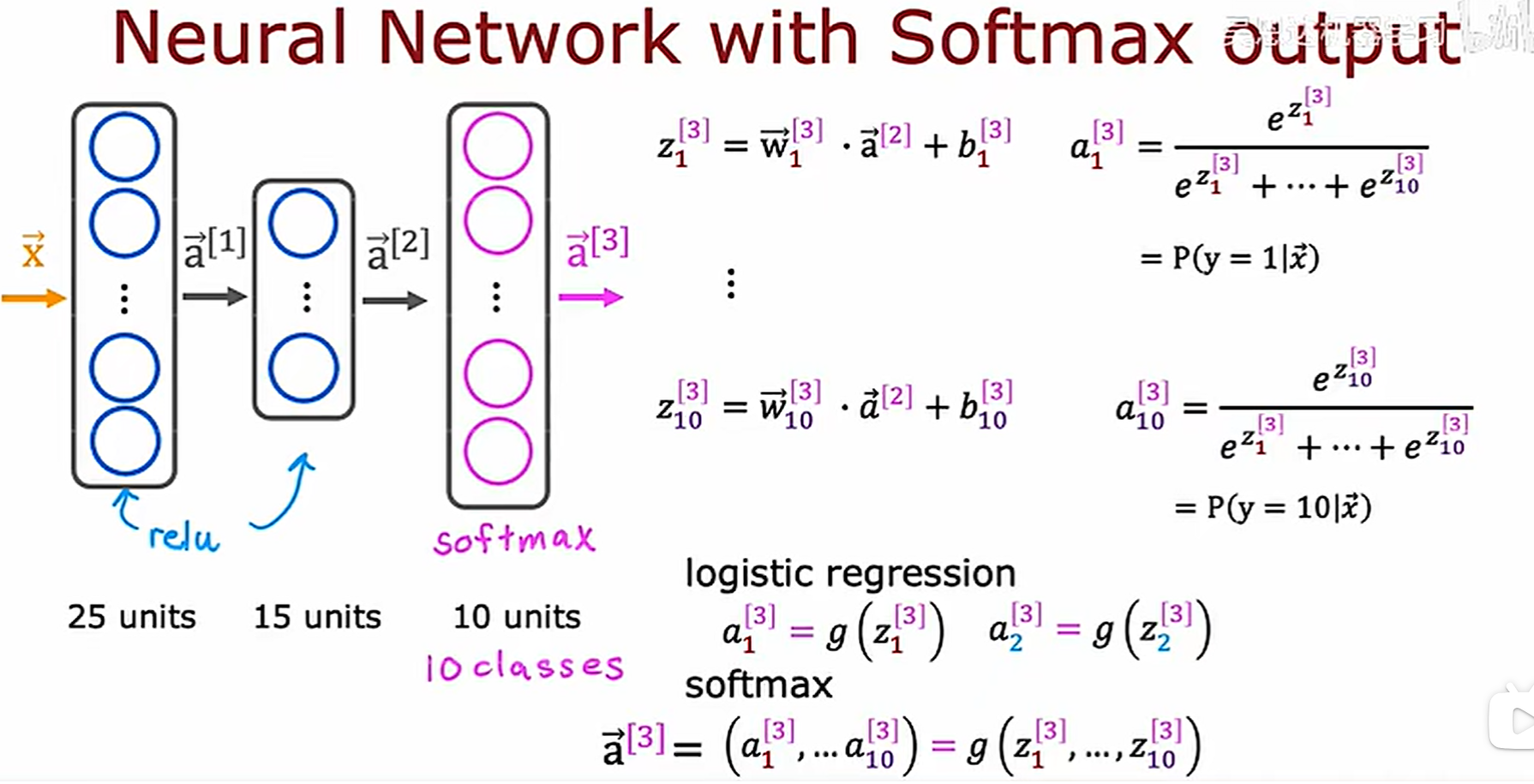
写成代码的形式:

数字精确度问题:

通过这个例子知道,虽然我们计算softmax成本函数的方法是正确的,还有一种更加准确的计算方法可以去减少误差
对于logistics回归

对于softmax

完整的tensorflow代码为:

多标签输出分类问题(注意和多分类问题的区别)
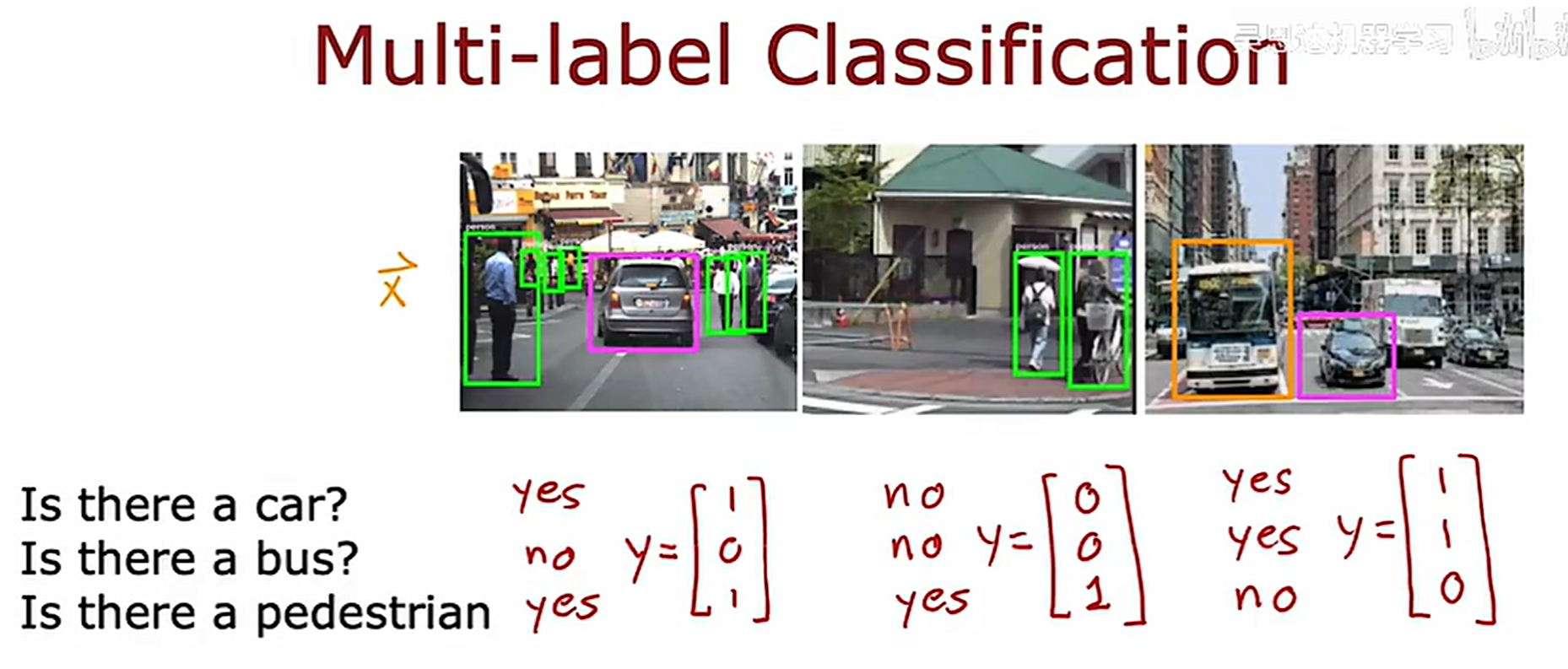
解决这种问题的一种方法是把它看作三个完全独立的机器学习问题,建立神经网络检测是否有车?是否有公交?等
还有一种方法是训练一个可以直接输出三个结果的神经网络

P69-P73
Adam算法
梯度下降是一种最小化成本函数的方法,下面介绍其它的方法
有一种方法叫做Adam algorithm可以自动调整学习率

算法的原理是:如果w和b能够朝着一个大致相同的方向移动,那么就提高学习率,反之,降低学习率,将其应用在MNIST的例子中,代码如下:在compile中增加一个优化器的参数即可,同时包含了初始的学习率

更多类型的层
到目前为止,我们使用的所有神经网络层都是密集层型的,下面给出一个不同类型的神经网络层的例子
密集层

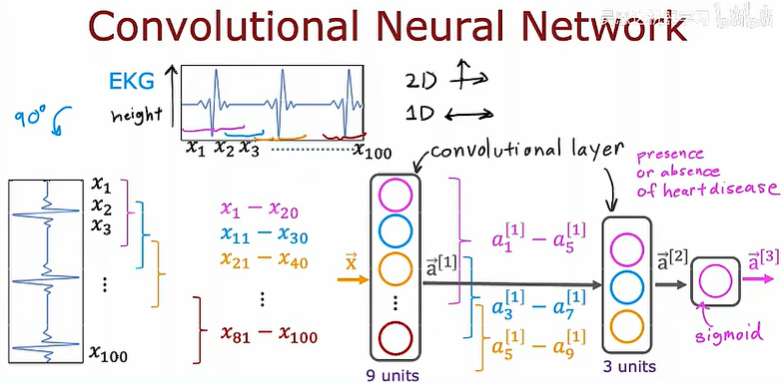
卷积层

卷积神经网络
卷积神经网络(CNN)是一种深度学习模型,主要用于处理具有类似网格结构的数据,如图像。CNN通过使用卷积层自动学习空间层次的特征,无需手动特征提取。卷积层内的卷积操作帮助模型学习图像中的小部分,然后将这些局部特征组合成更高级的形式,以实现复杂任务的学习
核心组件介绍
卷积层:使用一组可学习的滤波器来扫描输入数据,每个滤波器负责提取一种特定的特征。
激活函数:引入非线性,使网络能够学习复杂的模式,常用的激活函数有ReLU。
池化层:降低特征图的空间维度,减少计算量和参数数量,防止过拟合。
全连接层:将前面卷积层和池化层提取到的特征图转换为一维特征向量,进行最终的分类或回归分析。
调试学习算法

模型评估
将数据集分为训练集和测试集
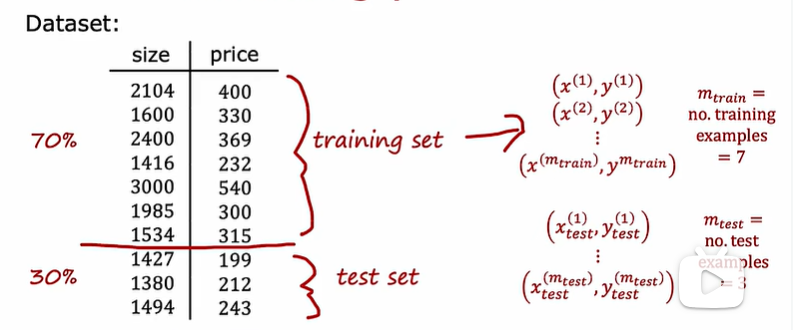
然后分别计算误差

对于分类问题(使用分类的成本函数)

模型选择

此时有一个问题,这里的测试集主要目的是为了挑选在测试集上表现最好的模型,也就是说最后得到模型之后,这个值一定是最小的,但是这个值是被挑选出来的,并不能真正反映模型的性能
还有一种优化的方法是把数据集分为三个部分,除了训练集和测试集,加上一个交叉验证集

此时:三部分数据集的各功能就如下所示:
训练集 (训练阶段)
用于构建我们的模型,我们的模型在训练集上进行学习,通常在这个阶段我们可以有多种方法进行训练
验证集 (模型挑选阶段)
用于挑选最优模型超参的样本集合:使用验证集可以得到反向传播什么时候结束以及超参怎么设置最合理。主要目的是为了挑选在验证集上表现最好的模型。
测试集 (验证阶段 评估泛化误差)
在我们挑选好验证集上表现最好的模型之后,用于评估该模型泛化能力的数据集。

P74-P79
偏差和方差
这部分我没看太懂网课,因为没字幕,但是有一个博客写得很明白,链接如下:
诊断偏差与方差
诊断偏差和方差
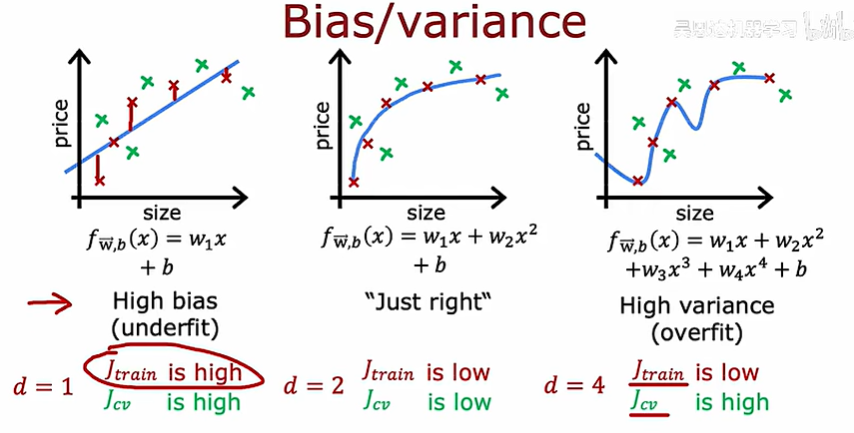
欠拟合为高偏差,过拟合为高方差

当 Jtrain(θ) ≈ Jcv(θ),但两者都非常高时,是模型欠拟合导是高偏差引起的,可以适当增加多项式次数解决
当 Jcv(θ) >> Jtrain(θ),是由于模型过拟合导致高方差引起,可以通过增加样本数据量解决
接下来看看正则化参数λ对偏差和方差的影响:

如图所示,当λ很大时,会发生高偏差,另一个极端,当λ很小时,会发生高方差
具体的Jtrain和Jcv与λ的定性关系,如下所示

建立表现基准
误差达到多大算大?达到多大算小?这时需要建立一个对比的标准去判断一个新算法的性能,可以根据下面三个方面去对比

当然也可以结合上述的基准去研究前面学习的偏差和方差

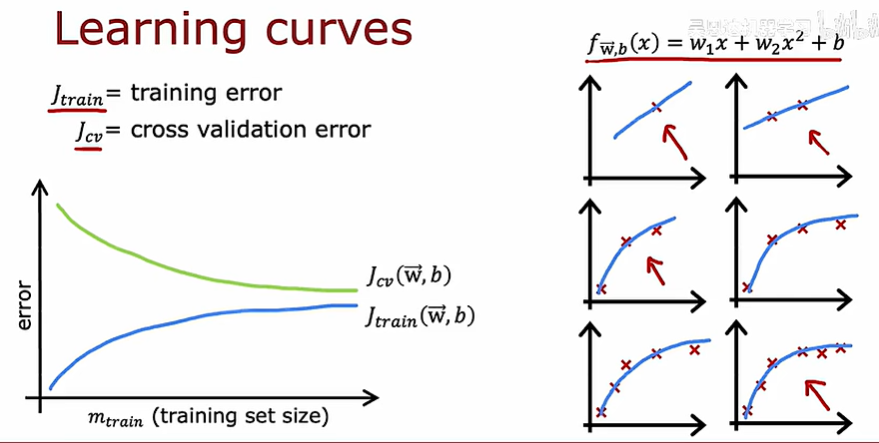
学习曲线
学习曲线是用来帮助理解算法如何工作的一种方法,如下所示,对于二次多项式,当增加训练集的数量时,Jtrain和Jcv的变化
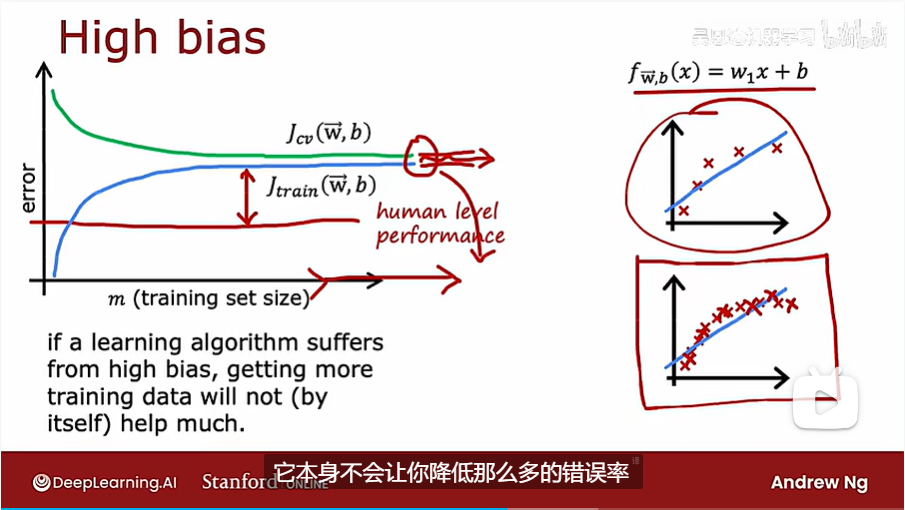
对于高偏差的算法,就算增大数据集的量,也不能明显地改善算法的性能
而对于高方差的曲线,增大数据集数量,有利于改善算法,使学习的效果达到表现基准左右
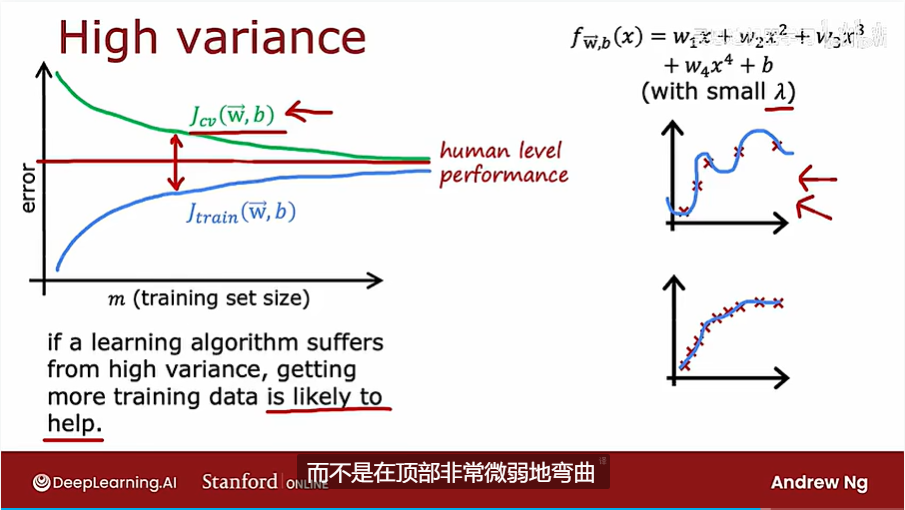
在debug的时候,下面常见的六个操作对偏差和方差的影响关系如下

偏差和方差与神经网络
神经网络给了我们一种新的方法去解决高偏差和高方差的问题,如下所示:
更大的神经网络导致了更大的计算量,这也就促进了gpu等加速硬件的发展

只要合适的进行规则化,神经网络就不会出现方差过大的问题

规则化的神经网络tensorflow代码如下

相关文章:

吴恩达机器学习全课程笔记第四篇
目录 前言 P61-P68 激活函数 Softmax算法 P69-P73 Adam算法 更多类型的层 模型评估 P74-P79 偏差和方差 建立表现基准 学习曲线 偏差和方差与神经网络 前言 这是吴恩达机器学习笔记的第四篇,第三篇笔记请见: 吴恩达机器学习全课程笔记第…...

大数据分析师常用函数
常用函数 当进行大数据分析时,SQL中的函数非常丰富,以下是更详细的展开: 窗口函数 (Window Functions): ROW_NUMBER(): 为结果集中的每一行分配一个唯一的整数,用于排序。RANK(): 为结果集中的每一行分配一个排名,相同值会有相同的排名,但会跳过相同排名数量。DENSE_RAN…...
MySQL 主从读写分离入门——基本原理以及ProxySQL的简单使用
一、读写分离工作原理 读写分离的工作原理:在大型网站业务中,当单台数据库无法满足并发需求时,通过主从同步方式同步数据。设置一台主服务器负责增、删、改,多台从服务器负责查询,从服务器从主服务器同步数据以保持一…...

ROS2从入门到精通:理论与实战
ROS是什么? 随着人工智能技术的飞速发展与进步,机器人的智能化已经成为现代机器人发展的终极目标。机器人发展的速度在不断提升,应用范围也在不断拓展,例如自动驾驶、移动机器人、操作机器人、信息机器人等。机器人系统是很多复杂…...

docker 安装minio 一脚shell脚本
要创建一个用于安装Minio的Docker的Shell脚本,你可以按照以下步骤进行。这个脚本会执行以下操作: 拉取Minio的Docker镜像。创建一个Docker容器并映射端口。设置Minio的访问密钥和秘密密钥。持久化存储数据到本地目录。 以下是一个简单的Shell脚本示例&…...

【数据库】mybatis使用总结
文章目录 1. 批量插入、检索<foreach>2. <if> 判断等于情况3. 模糊查询(pgsql为例)4. 分页5. <resultMap > 中collection 和association 6. no conflict do update 1. 批量插入、检索<foreach> <insert id"insertSystemService" >in…...

VR元宇宙的概念|VR体验店加盟|虚拟现实设备销售
VR元宇宙是一个结合了虚拟现实(Virtual Reality)和增强现实(Augmented Reality)等技术的概念,代表着一个虚拟的多维度世界。它是一个由数字化的空间构成的虚拟环境,可以通过虚拟现实设备进行交互和探索。 元…...
MySQL进阶:全局锁、表级锁、行级锁总结
👨🎓作者简介:一位大四、研0学生,正在努力准备大四暑假的实习 🌌上期文章:MySQL进阶:MySQL事务、并发事务问题及隔离级别 📚订阅专栏:MySQL进阶 希望文章对你们有所帮助…...

Python用函数实现代码复用
归纳编程学习的感悟, 记录奋斗路上的点滴, 希望能帮到一样刻苦的你! 如有不足欢迎指正! 共同学习交流! 🌎欢迎各位→点赞 👍 收藏⭐ 留言📝 生命对某些人来说是美丽的,…...

2024年腾讯云优惠代金券领取入口整理汇总,收藏级笔记
腾讯云优惠代金券领取入口共三个渠道,腾讯云新用户和老用户均可领取8888元代金券,可用于云服务器等产品购买、续费和升级使用,阿腾云atengyun.com整理腾讯云优惠券(代金券)领取入口、代金券查询、优惠券兑换码使用方法…...
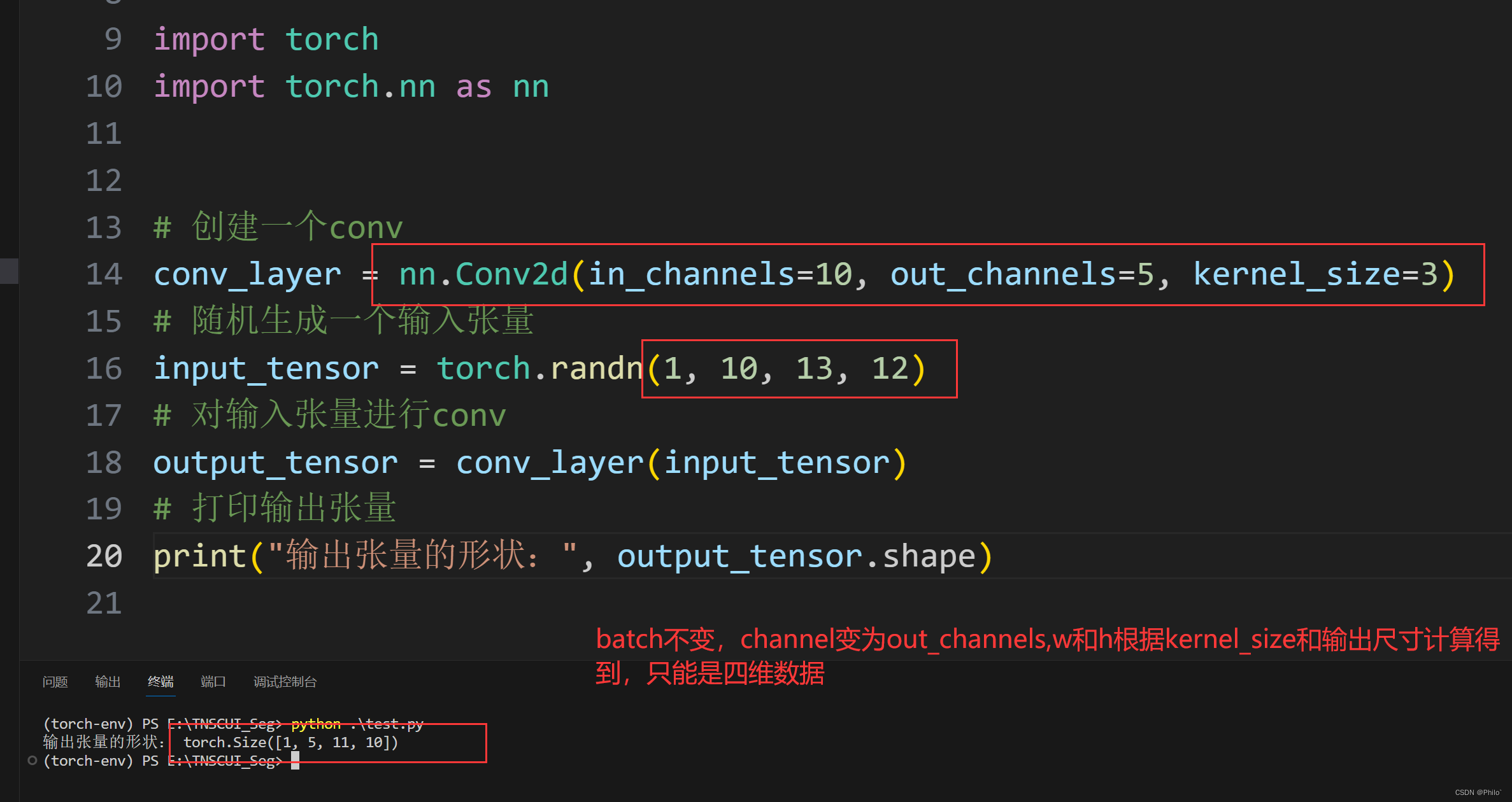
nn.Linear() 使用提醒
原本以为它是和nn.Conv2d()一样,就看第二个维度的数值,今天才知道,它是只看最后一个维度的数值!!! 例子1 Descripttion: Result: Author: Philo Date: 2024-02-27 14:33:50 LastEditors: Philo LastEditT…...

python difflib --- 计算差异的辅助工具
此模块提供用于比较序列的类和函数。 例如,它可被用于比较文件,并可产生多种格式的不同文件差异信息,包括 HTML 和上下文以及统一的 diff 数据。 有关比较目录和文件,另请参阅 filecmp 模块。 class difflib.SequenceMatcher 这…...

HTML5浮动
1.标准文档流组成 块级元素(block) 内联元素(inline) 2.display属性 作用:指定HTML标签的显示方式 常用属性 值 说明 block 块级元素的默认值,元素会被显示为块级元素,该元素前后会带有换行…...
Unity 向量计算、欧拉角与四元数转换、输出文本、告警、错误、修改时间、定时器、路径、
using System.Collections; using System.Collections.Generic; using UnityEngine;public class c2 : MonoBehaviour {// 定时器float t1 0;void Start(){// 向量Vector3 v1 new Vector3(0, 0, 2);Vector3 v2 new Vector3(0, 0, 3);// 计算两个向量的夹角Debug.Log(Vector3…...

前端实现浏览器打印
浏览器的print方法直接调用会打印当前页面的所有元素,使用iframe可以实现局部打印所需要的模块。 组件printView,将传入的信息放入iframe中,调用浏览器的打印功能 <template><div class"print"><iframeid"if…...

iOS卡顿原因与优化
iOS卡顿原因与优化 1. 卡顿简介 卡顿: 指用户在使用过程中出现了一段时间的阻塞,使得用户在这一段时间内无法进行操作,屏幕上的内容也没有任何的变化。 卡顿作为App的重要性能指标,不仅影响着用户体验,更关系到用户留…...
关于synchronized介绍
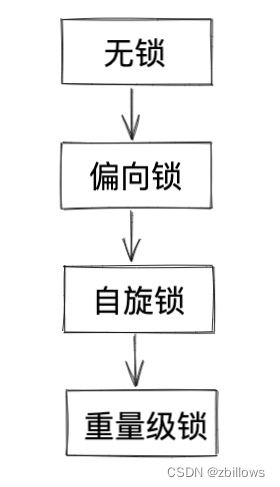
synchronized的特性 1. 乐观锁/悲观锁自适应,开始时是乐观锁,如果锁冲突频繁,就转换为悲观锁 2.轻量级/重量级锁自适应 开始是轻量级锁实现,如果锁被持有的时间较长,就转换成重量级锁 3.自旋/挂起等待锁自适应 4.不是读写锁 5.非公平锁 6,可重入锁 synchronized的使用 1&#…...

NCDA设计大赛获奖作品剖析:UI设计如何脱颖而出?
第十二届大赛简介 - 未来设计师全国高校数字艺术设计大赛(NCDA)开始啦!视觉传达设计命题之一: ui 设计,你想知道的都在这里。为了让大家更好的参加这次比赛,本文特别为大家整理了以往NCDA大赛 UI 设计的优秀获奖作品&a…...

软考中级 软件设计师备考经验
考试介绍 软考中级的软件设计师需要考两个部分,选择题和大题,每科满分75,需要在同一次考试中两科同时大于等于45分才算通过。考试的内容包括计算机组成原理、数据结构、数据库、专业英语、信息安全、计算机网络等,范围比较广但考…...

Python猜数字小游戏
下面这段代码是一个简单的数字猜测游戏,其中计算机已经提前计算出了414 // 23的结果并存储在变量num中。然后,程序会提示用户来猜测这个结果。 以下是代码的主要步骤和功能: 初始化: num 414 // 23:计算414除以23的整…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...

聚六亚甲基单胍盐酸盐市场深度解析:现状、挑战与机遇
根据 QYResearch 发布的市场报告显示,全球市场规模预计在 2031 年达到 9848 万美元,2025 - 2031 年期间年复合增长率(CAGR)为 3.7%。在竞争格局上,市场集中度较高,2024 年全球前十强厂商占据约 74.0% 的市场…...
