【leetcode】圆圈中最后剩下的数字
目录
1. 问题
2. 思路
3. 代码
4. 运行
1. 问题
本题即为典型的约瑟夫问题,通过递推公式倒推出问题的解。原始问题是从n个人中每隔m个数踢出一个人,原始问题变成从n-1个人中每隔m个数踢出一个人……
示例 1:
输入: n = 5, m = 3 输出: 3
示例 2:
输入: n = 10, m = 17 输出: 2
2. 思路
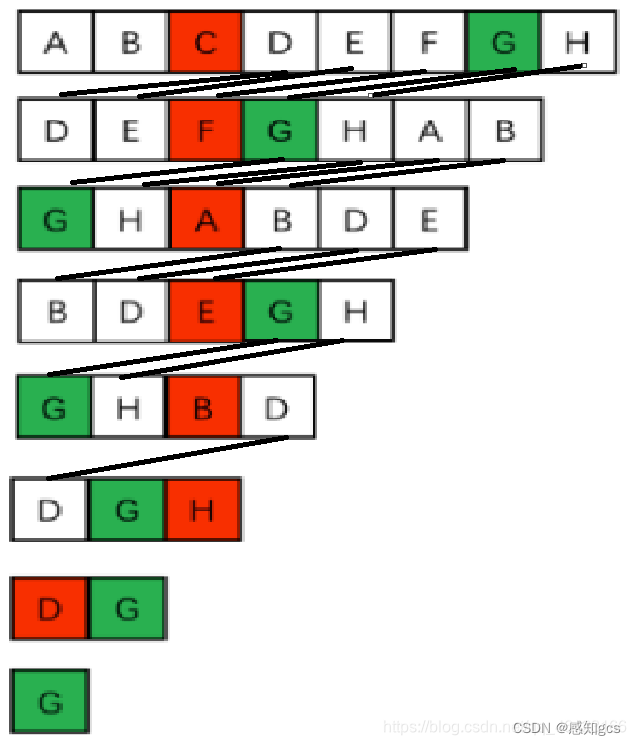
第一行表示每个人的下标,现在要从11个人中删除报数为3的人,从图中可以可看出最后7是胜利者。分析其中的规律:
第一轮中,11个人中胜利者7的角标是6;
第二轮中,10个人中胜利者7的角标是3;
第三轮中,9个人中胜利者7的角标是0;
第四轮中,8个人中胜利者7的角标是6;
第五轮中,7个人中胜利者7的角标是3;
第六轮中,6个人中胜利者7的角标是0;
第七轮中,5个人中胜利者7的角标是3;
第八轮中,4个人中胜利者7的角标是0;
第九轮中,3个人中胜利者7的角标是1;
第十轮中,2个人中胜利者7的角标是1;
第十一轮中,1个人中胜利者7的角标是0;
从第十一轮中倒推到第一轮:
从第十一轮中推出第十轮的角标数,f(2,3) = (f(1,3) + m) % 2 =(0+3) % 2 = 1
从第十轮中推出第九轮的角标数,f(3,3) = (f(2,3) + m) % 3 =(1+3) % 3 = 1
从第九轮中推出第八轮的角标数,f(4,3) = (f(3,3) + m) % 4 =(1+3) % 4 = 0
懒得写了…….
结论:从n个人中每隔m删除一人,递推公式为 f(n,m) = (f(n-1,m)+m) % n
3. 代码
#include <iostream>
using namespace std;class Solution {
public:// n表示多少个人,m表示随机数int LastRemaining_Solution(int n, int m){// 特殊输入if (n == 0 || m < 0) return -1;// 递推公式计算int res = 0;for (int i = 1; i <= n; i++){res = (res + m) % i;cout << res << endl;}return res;}
};
int main()
{int n = 11;int m = 3;Solution solution;solution.LastRemaining_Solution(n, m);return 0;
}
4. 运行
相关文章:

【leetcode】圆圈中最后剩下的数字
目录 1. 问题 2. 思路 3. 代码 4. 运行 1. 问题 本题即为典型的约瑟夫问题,通过递推公式倒推出问题的解。原始问题是从n个人中每隔m个数踢出一个人,原始问题变成从n-1个人中每隔m个数踢出一个人…… 示例 1: 输入: n 5, m 3 输出: 3…...

利用python批量将.shp文件转换坐标生成.geojson文件,再将.geojson转换成.csv文件,最后将csv文件插入数据库表
第一步:.shp批量转.geojson # author: JMY # 创建时间: 2024/2/26 17:12 # 批量将.shp文件生成geojson文件并转换坐标为3857import os import geopandas as gpd# 定义输入和输出文件夹路径 input_folder shp文件 output_folder geojson文件# 定义输入和输出坐标系…...
远程服务器Ubuntu 18.04安装VNC远程桌面
一、安装vnc 1.安装图形化界面工具 # 安装过程中会弹窗让选择配置,选lightdm sudo apt install ubuntu-desktop sudo apt-get install gnome-panel gnome-settings-daemon metacity nautilus gnome-terminal 2.安装vnc sudo apt-get install x11vnc3.安装LightD…...
)
30天自制操作系统(第23天)
23.1 编写malloc 参考第22天的内容,在绘制窗口前先分配了150*50个字节大小的内存,所以导致该文件经编译后有7.6k左右,能否在其中使用指针呢?当需要开辟空间时,移动指针即可。在之前的章节中也有函数memman_alloc函数可…...

基于Rust语言,和WebAssembly技术,与JavaScript结合,的具体应用场景
基于Rust语言与WebAssembly(Wasm)技术并与JavaScript结合,可以应用于多个场景,特别是在需要高性能和/或低级系统访问的情况下。下面是一些具体的应用场景: 性能密集型任务: Rust加上Wasm适合执行计算密集型任务&#x…...
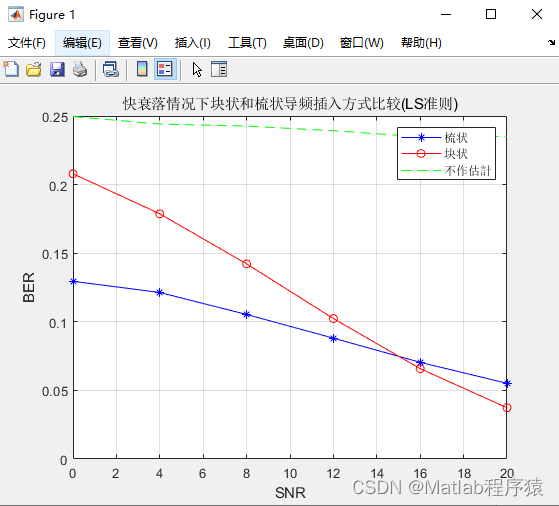
【MATLAB源码-第154期】基于matlab的OFDM系统多径信道下块状和梳妆两种导频插入方式误码率对比仿真。
操作环境: MATLAB 2022a 1、算法描述 OFDM(Orthogonal Frequency Division Multiplexing,正交频分复用)是一种高效的无线信号传输技术,广泛应用于现代通信系统,如Wi-Fi、LTE和5G。OFDM通过将宽带信道划分…...

Linux 下 socket 编程介绍及 TCP 客户端与服务端创建示例
目录 socket 编程接口TCP 服务端TCP 客户端更多内容 本文介绍了 Linux 下的 socket 编程,及总结了使用 socket 接口实现 TCP 服务端和客户端的示例代码。 socket 编程接口 socket() 函数:用于创建一个新的 socket 描述符: int socket(int …...
JetBrains Gateway Github Copilot 客户端插件和主机插件
JetBrains Gateway可以通过插件支持Github Copilot(需另行注册)。 需要安装插件 客户端,而非插件 主机,如图所示: 大概是因为代码显示在客户端(运行在本地的IDE)?...
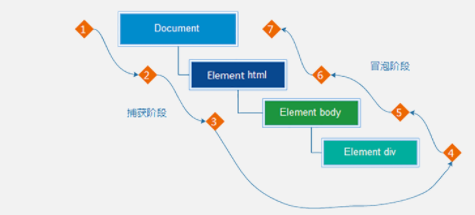
【web APIs】3、(学习笔记)有案例!
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、概念其他事件页面加载事件元素滚动事件页面尺寸事件 元素尺寸与位置 二、案例举例电梯导航 前言 掌握阻止事件冒泡的方法理解事件委托的实现原理 一、概念…...

使用css reset 还是使用Normalize.css
文章目录 使用css reset 还是使用Normalize.cssCSS Reset:Normalize.css:总结Normalize.css 的使用(例如Vue 3.0 和 Vue CLI 4.x 项目)1.安装2.main.js 中导入3.测试引用是否成功。 使用css reset 还是使用Normalize.css 使用 CSS Reset 还是 Normalize…...
(bug提问、bug描述))
英语中的提问方式(问法)(bug提问、bug描述)
文章目录 英语提问方式一、单词、短语、句子的意思1.1 提问单词的意思1.2 提问短语的意思1.3 提问句子的意思 二、在编程中提问2.1 提问bug2.2 请求代码帮助 如何提出反问句1. 构建反问句的基本结构2. 提问反问句的方法3. 理解反问句的意图 在口语中提问:确保清晰度…...
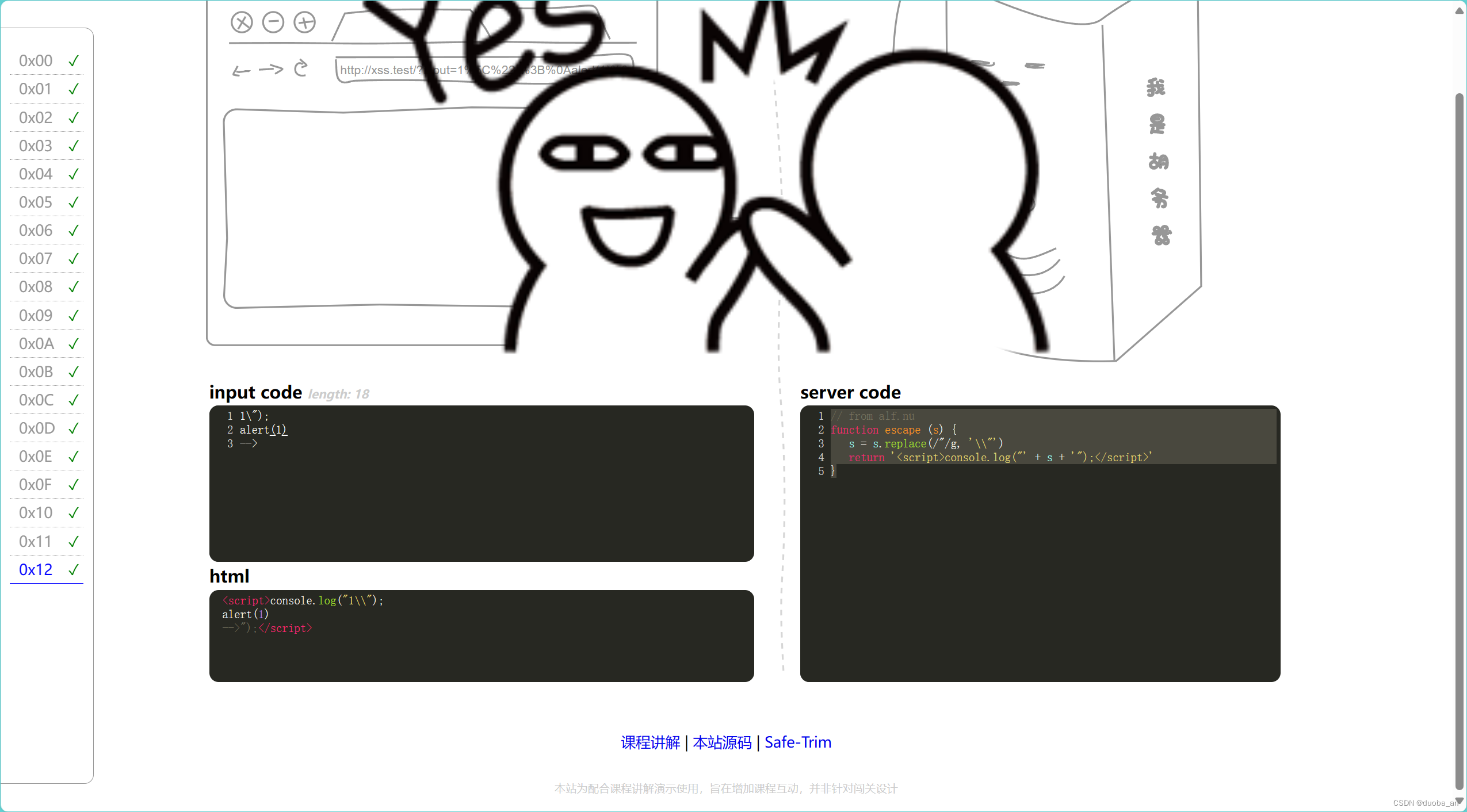
xss.haozi.me靶机练习
目录 第零关: 第一关: 第二关: 第三关: 第四关: 第五关: 第六关: 第七关: 第八关: 第九关: 第十关: 第十一关: 第十二关…...
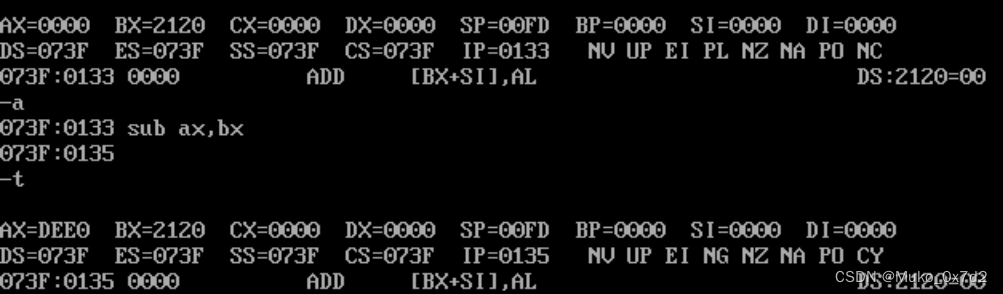
2.1 mov、add和sub加减指令实操体验
汇编语言 1. mov操作 1.1 mov移动值 mov指令把右边的值移动到左边 mount c d:masm c: debug r ax 0034 r 073f:0100 mov ax,7t1.2 mov移动寄存器的值 把右边寄存器的值赋值给左边的寄存器 a 073f:0105 mov bx,axt1.3 mov高八位(high)和低八位&am…...

计算机设计大赛 深度学习机器视觉车道线识别与检测 -自动驾驶
文章目录 1 前言2 先上成果3 车道线4 问题抽象(建立模型)5 帧掩码(Frame Mask)6 车道检测的图像预处理7 图像阈值化8 霍夫线变换9 实现车道检测9.1 帧掩码创建9.2 图像预处理9.2.1 图像阈值化9.2.2 霍夫线变换 最后 1 前言 🔥 优质竞赛项目系列,今天要分…...
有中间件的各类链接和官网信息和漏洞库以及配置问题和开源工具)
中间件安全(概述)有中间件的各类链接和官网信息和漏洞库以及配置问题和开源工具
分类主要包括Apache、IIS、Tomcat、weblogic、websphere、Jboss等相关的技术知识和实践。 以Apache为例讲一讲如何保证中间件安全 中间件安全是指保护中间件软件和服务的安全性,防止被恶意攻击或者滥用。中间件软件是指在操作系统和应用程序之间提供通信和集成功能…...
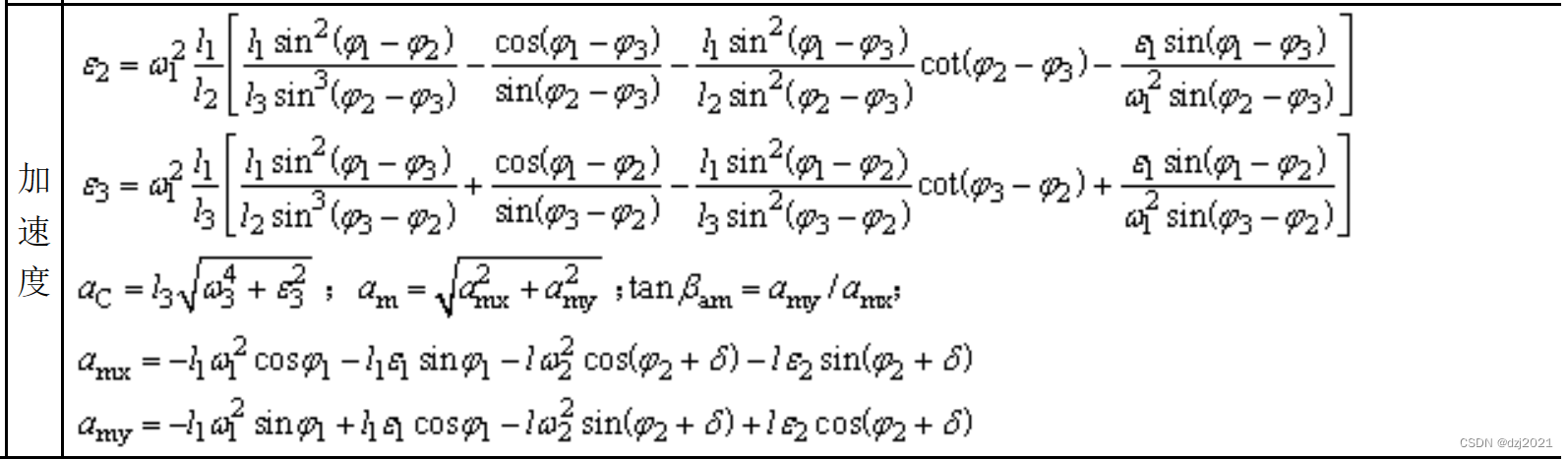
Unity铰链四杆机构设计和运动仿真
一、效果图 设定好各边长度和转速后,点击【设置并启动】,自动生成一个机构模型,并按照原理进行运转 二、铰链四杆机构介绍 机架:A和D是固定位置,叫做机架。 曲柄:B点绕A点旋转,构成曲柄。 连…...

Python爬虫——解析常用三大方式之Xpath
目录 Xpath 安装xpath 安装lxml库 导入lxml库 解析本地文件 etree.parse() 解析服务器响应文件 etree.HTML() xpath基本语法 小案例:获取百度首页的百度一下 大案例:爬取站长素材图片 总结 Xpath 安装xpath 首先要学会安…...

C#判断DataTable1 A列的集合是否为DataTable2 B列的集合的子集
DataSet ds2 (DataSet)res2.Anything; // 检查 集合B是否为集合A的子集 var table1MaterialCodes ds.Tables[2].AsEnumerable().Select(row > row["Code"]).ToList(); //DataSet1 表Code列集合A var table2MaterialCodes ds2.Tables[0].AsEnumerable().Selec…...
VirtualBox 桥接网卡 未指定 “未能启动虚拟电脑Ubuntu,由于下述物理网卡未找到:”
解决办法,安装虚拟网卡,win11查找方式:控制面板→网络和共享中心→更改适配器设置 此时出现下面情况就算安装成功 但是如果报错:找不到指定的模块 则按下面步骤删除干净垃圾重新上面操作 先安装CCleaner, 链接:CCleaner Makes Y…...

基于yolov5的电瓶车和自行车检测系统,可进行图像目标检测,也可进行视屏和摄像检测(pytorch框架)【python源码+UI界面+功能源码详解】
功能演示: 基于yolov5的电瓶车和自行车检测系统_哔哩哔哩_bilibili (一)简介 基于yolov5的电瓶车和自行车检测系统是在pytorch框架下实现的,这是一个完整的项目,包括代码,数据集,训练好的模型…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...
