CF1561C Deep Down Below 题解
CF1561C Deep Down Below 题解
- 题目
- 链接
- 字面描述
- Deep Down Below
- 题面翻译
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- 思路
- TLE算法
- 具体思想
- TLE特例
- AC思想
- 代码实现
- 备注
题目
链接
https://www.luogu.com.cn/problem/CF1561C
字面描述
Deep Down Below
题面翻译
TTT 组数据,每次给定 nnn 个任务,第 iii 个任务给定 kik_iki 个怪物,每个怪物有一个能力值 ai,ja_{i,j}ai,j 你要按顺序把这 kik_iki 个怪物杀死,你能杀死一个怪物当且仅当你的能力值严格大于怪物的能力值,杀死一个怪物后,你的能力值将会 +1+1+1。
你可以按任意顺序完成这 nnn 个任务,你需要确定最小的初始能力值。
T≤105,n≤105,ki≤105,∑ki≤105,ai,j≤109T\leq 10^5,n\leq 10^5,k_i\leq10^5,\sum k_i\leq 10^5,a_{i,j}\leq 10^9T≤105,n≤105,ki≤105,∑ki≤105,ai,j≤109。
题目描述
In a certain video game, the player controls a hero characterized by a single integer value: power. The hero will have to beat monsters that are also characterized by a single integer value: armor.
On the current level, the hero is facing $ n $ caves. To pass the level, the hero must enter all the caves in some order, each cave exactly once, and exit every cave safe and sound. When the hero enters cave $ i $ , he will have to fight $ k_i $ monsters in a row: first a monster with armor $ a_{i, 1} $ , then a monster with armor $ a_{i, 2} $ and so on, finally, a monster with armor $ a_{i, k_i} $ .
The hero can beat a monster if and only if the hero’s power is strictly greater than the monster’s armor. If the hero can’t beat the monster he’s fighting, the game ends and the player loses. Note that once the hero enters a cave, he can’t exit it before he fights all the monsters in it, strictly in the given order.
Each time the hero beats a monster, the hero’s power increases by $ 1 $ .
Find the smallest possible power the hero must start the level with to be able to enter all the caves in some order and beat all the monsters.
输入格式
Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 10^5 $ ). Description of the test cases follows.
The first line of each test case contains a single integer $ n $ ( $ 1 \le n \le 10^5 $ ) — the number of caves.
The $ i $ -th of the next $ n $ lines contains an integer $ k_i $ ( $ 1 \le k_i \le 10^5 $ ) — the number of monsters in the $ i $ -th cave, followed by $ k_i $ integers $ a_{i, 1}, a_{i, 2}, \ldots, a_{i, k_i} $ ( $ 1 \le a_{i, j} \le 10^9 $ ) — armor levels of the monsters in cave $ i $ in order the hero has to fight them.
It is guaranteed that the sum of $ k_i $ over all test cases does not exceed $ 10^5 $ .
输出格式
For each test case print a single integer — the smallest possible power the hero must start the level with to be able to enter all the caves in some order and beat all the monsters.
样例 #1
样例输入 #1
2
1
1 42
2
3 10 15 8
2 12 11
样例输出 #1
43
13
提示
In the first test case, the hero has to beat a single monster with armor $ 42 $ , it’s enough to have power $ 43 $ to achieve that.
In the second test case, the hero can pass the level with initial power $ 13 $ as follows:
- enter cave $ 2 $ :
- beat a monster with armor $ 12 $ , power increases to $ 14 $ ;
- beat a monster with armor $ 11 $ , power increases to $ 15 $ ;
- enter cave $ 1 $ :
- beat a monster with armor $ 10 $ , power increases to $ 16 $ ;
- beat a monster with armor $ 15 $ , power increases to $ 17 $ ;
- beat a monster with armor $ 8 $ , power increases to $ 18 $ .
思路
TLE算法
具体思想
本人最初的想法十分的朴素,针对nnn个任务维护nnn个队首指针。
- 每次比较出nnn个任务队首怪兽的最小值
- 与当前预算的能力值比较是否能继续打怪,是 -> 继续 ,否 -> 加到怪兽能力值+1即可。
TLE特例
如果有1e5个任务,每个任务只有1个怪兽。
按此算法:
时间复杂度退化:O(n⋅Σk)≈1e10O(n·Σk)≈1e10O(n⋅Σk)≈1e10 TLE ! ! !
AC思想
2阶段处理
- 算出每组打怪加能力的情况下每一个怪兽所对应初始能力值,并取max
- 将nnn个max从小到大排序,依次循环,看每个max加上对应任务里的元素数(能加多少次能力),是否能满足下一个max,是 -> continue ,否 -> 加到下一个max。
时间复杂度:O(Σk⋅log(Σk))≈2e6O(Σk·log(Σk))≈2e6O(Σk⋅log(Σk))≈2e6
阶段线性处理,tql !
代码实现
#include<bits/stdc++.h>
using namespace std;const int maxn=1e5+10;
int t,n,ans;
int k[maxn];
vector<int>e[maxn];
struct node{int v,cnt;
}a[maxn];
inline bool cmp(node p,node q){return p.v<q.v;}
int main(){scanf("%d",&t);while(t--){scanf("%d",&n);for(int i=1;i<=n;i++){e[i].clear();scanf("%d",&k[i]);//算每组的最大值for(int j=1;j<=k[i];j++){int x;scanf("%d",&x);x=x+2-j;if(j!=1)x=max(x,e[i][j-2]);e[i].push_back(x);}a[i].v=e[i][k[i]-1];//最大值的最小取值a[i].cnt=k[i];//任务里的怪兽数//printf("%d = %d %d\n",i,a[i].v,a[i].cnt);}sort(a+1,a+n+1,cmp);ans=a[1].v;int l=ans+a[1].cnt;//排序比较for(int i=2;i<=n;i++){if(l<a[i].v){ans=ans+a[i].v-l;l=a[i].v;}l+=a[i].cnt;}printf("%d\n",ans);}return 0;
}
备注
写入好题本
相关文章:

CF1561C Deep Down Below 题解
CF1561C Deep Down Below 题解题目链接字面描述Deep Down Below题面翻译题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1提示思路TLE算法具体思想TLE特例AC思想代码实现备注题目 链接 https://www.luogu.com.cn/problem/CF1561C 字面描述 Deep Down Below 题面翻译…...

秒杀项目之服务调用分布式session
目录 nginx动静分离 服务调用 创建配置zmall-cart购物车模块 创建配置zmall-order订单模块 服务调用 spring session实战 什么是Spring Session 为什么要使用Spring Session 错误案例展示 配置spring-session 二级域名问题 用户登录 nginx动静分离 第1步ÿ…...
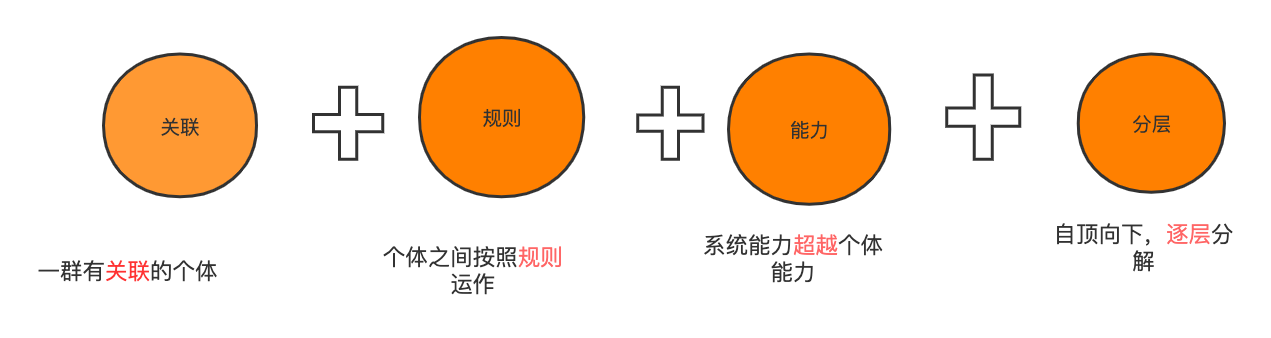
聊聊什么是架构,你理解对了吗?
什么是架构?软件有架构?建筑也有架构?它们有什么相同点和不同点? 下面咱们就介绍一下,容易混淆的几个概念 一、系统与子系统 系统 泛指由一群有关联的个体组成,根据某种规则运作,能完成个别元件不能单独完成的工作的群体。它的意思是 “总体”、“整体”或“联盟” 子系…...
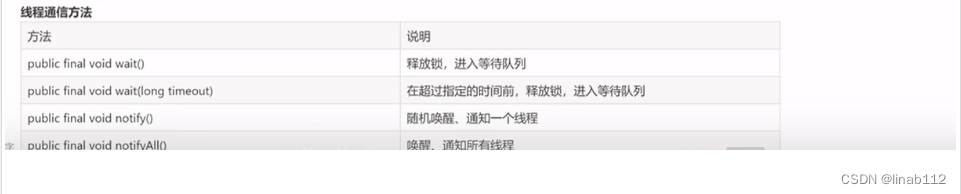
java多线程开发
1.并发和并行 并发:同一时间段内多个任务同时进行。 并行:同一时间点多个任务同时进行。 2.进程线程 进程(Process):进程是程序的一次动态执行过程,它经历了从代码加载、执行、到执行完毕的一个完整过程…...

杂记7--opencv的ar码模块学习
背景:项目需要用到marker知识,所以到官网上临时补一些知识。 概要:主要介绍marker一些接口的含义,纯属个人理解,有误则希望大佬不吝赐教 1、 涉及ar码操作学习,其头文件为: #include <op…...
[项目设计]高并发内存池
目录 1、项目介绍 2、高并发内存池整体框架设计 3、thread cache <1>thread cache 哈希桶对齐规则 <2>Thread Cache类设计 4、Central Cache <1>Central Cache类设计 5、page cache <1>Page Cache类设计 6、性能分析 <1>定长内存池实现…...
28岁才转行软件测试,目前32了,我的一些经历跟感受
我是92年的,算是最早的90后,现在跟你介绍的时候还恬不知耻的说我是90后,哈哈,计算机专业普通本科毕业。在一个二线城市,毕业后因为自身能力问题、认知水平问题,再加上运气不好,换过多份工作&…...
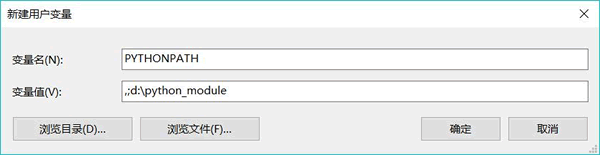
Python导入模块的3种方式
很多初学者经常遇到这样的问题,即自定义 Python 模板后,在其它文件中用 import(或 from...import) 语句引入该文件时,Python 解释器同时如下错误:ModuleNotFoundError: No module named 模块名意思是 Pytho…...
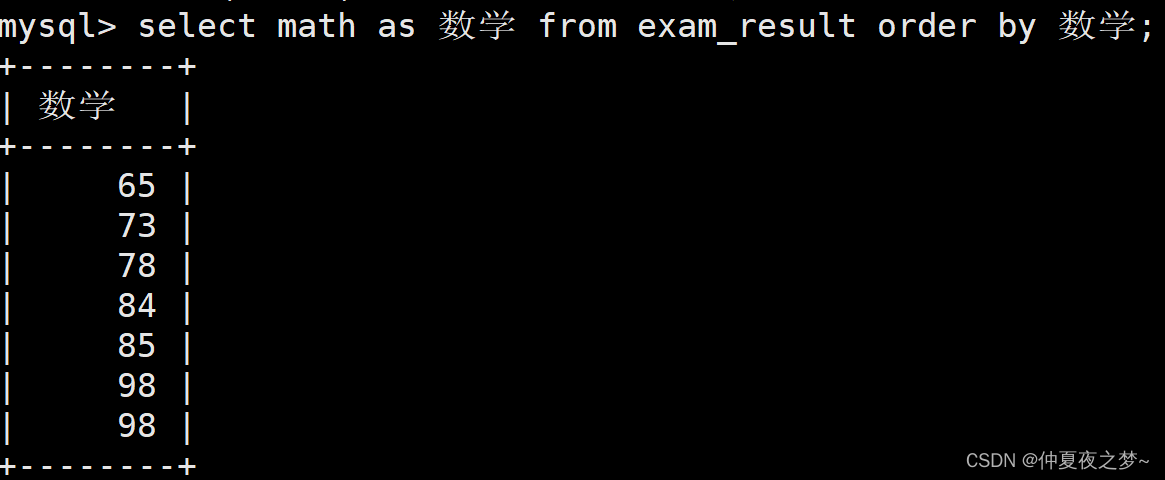
select 与 where、order by、limit 子句执行优先级比较
当 select 和 其他三种语句的一者或者多者同时出现时,他们之间是存在执行先后顺序的。 他们的优先级顺序是:where > select > order by > limit 目录 1、select 与 where 2、select 与 order by 3、order by 与 limit 4、优先级证明 1、s…...
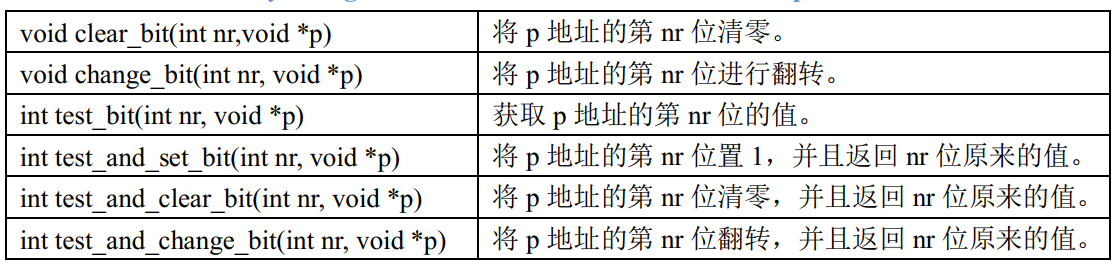
Linux内核并发与竞争-原子操作
一.原子操作的概念首先看一下原子操作,原子操作就是指不能再进一步分割的操作,一般原子操作用于变量或者位操作。假如现在要对无符号整形变量 a 赋值,值为 3,对于 C 语言来讲很简单,直接就是: a3但是 C 语言…...

Java笔记-泛型的使用
参考: Java 泛型,你了解类型擦除吗? 泛型的使用 1、泛型的定义 可以广泛使用的类型,一种较为准确的说法就是为了参数化类型,或者说可以将类型当作参数传递给一个类或者是方法。 2、泛型的使用 2.1泛型类 public c…...
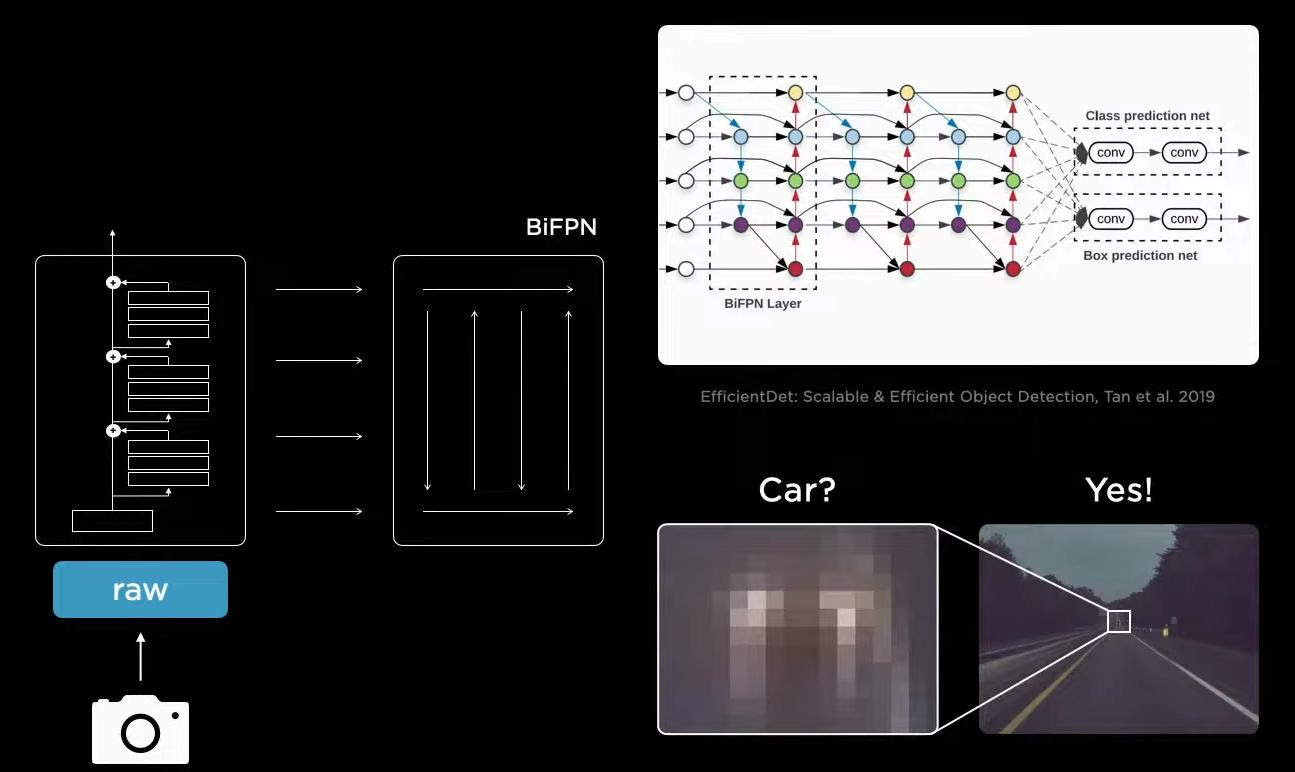
特斯拉无人驾驶解读
来源于Tesla AI Day Tesla无人驾驶算法的核心任务就是如何理解我们所看到的一切呢?也就是说,不使用高端的设备,比如激光雷达,仅仅使用摄像头就能够将任务做得很好。Tesla使用环绕型的8个摄像头获得输入。 第一步是特征提取模块Backbone,无论什么任务都离不开特征…...
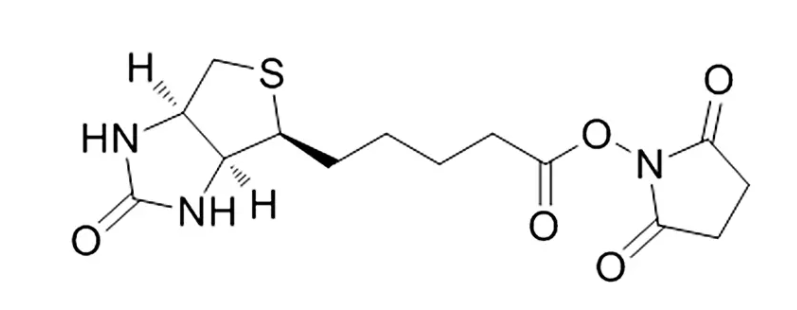
生物素-琥珀酰亚胺酯Biotin-NHS;CAS号:35013-72-0;可对溶液中的抗体,蛋白质和任何其他含伯胺的大分子进行简单有效的生物素标记。
结构式: 生物素-琥珀酰亚胺酯Biotin NHS CAS号:35013-72-0 英文名称:Biotin-NHS 中文名称:D-生物素 N-羟基琥珀酰亚胺酯;生物素-琥珀酰亚胺酯 CAS号:35013-72-0 密度:1.50.1 …...
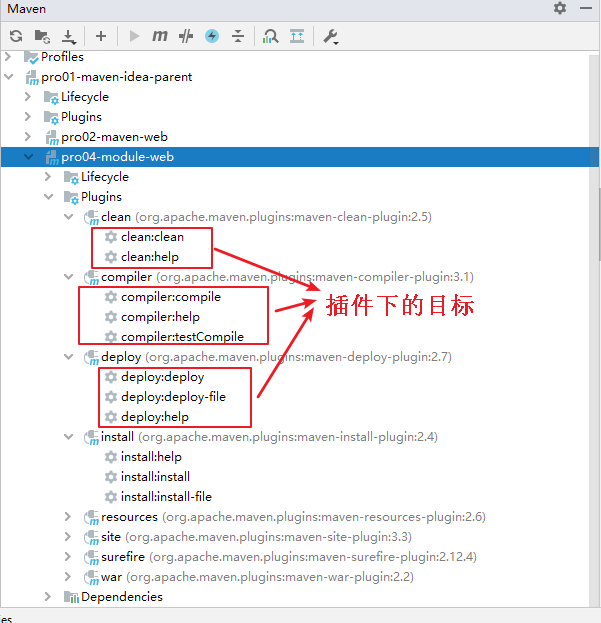
Maven_第五章 核心概念
目录第五章 其他核心概念1、生命周期①作用②三个生命周期③特点2、插件和目标①插件②目标3、仓库第五章 其他核心概念 1、生命周期 ①作用 为了让构建过程自动化完成,Maven 设定了三个生命周期,生命周期中的每一个环节对应构建过程中的一个操作。 …...

【深度学习】人脸识别工程化落地
文章目录前言1、facenet2、使用2.1.其它blog2.2 实践总结前言 老早以前就希望能写一篇关于人脸识别的工程化落地的案例,一年前做疲劳驾驶时使用的dlib插件,它封装好了,人脸检测、对齐、相似度计算三个部分,就是插件比较难装,但同时也少了很多…...
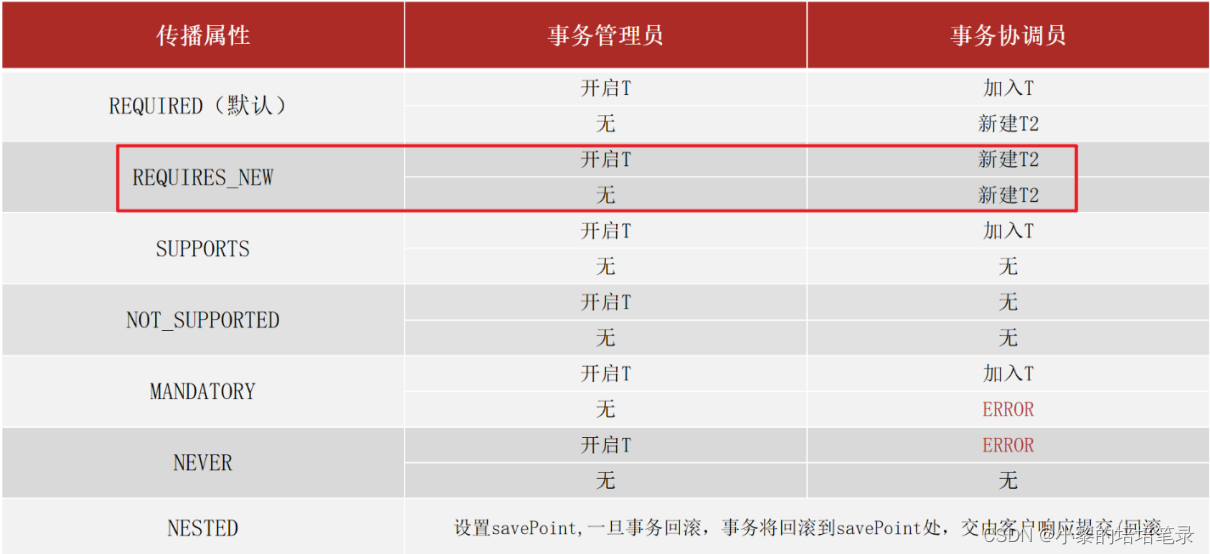
AOP面向切面编程思想。
目录 一、AOP工作流程 1、基本概念 2、AOP工作流程 二、AOP核心配置 1、AOP切入点表达式 2、AOP通知类型 三、AOP通知获取数据 1、获取参数 2、获取返回值 3、获取异常 四、AOP事务管理 1、Spring事务简介 2、Spring事务角色 3、事务属性 一、AOP工作流程 1、…...

实验7-变治技术及动态规划初步
目录 1.统计个数 2.数塔dp -A 3.Horspool算法 4.计数排序 5.找零问题1-最少硬币 1.统计个数 【问题描述】有n个数、每个元素取值在1到9之间,试统计每个数的个数 【输入形式】第一行,n的值;第二行...
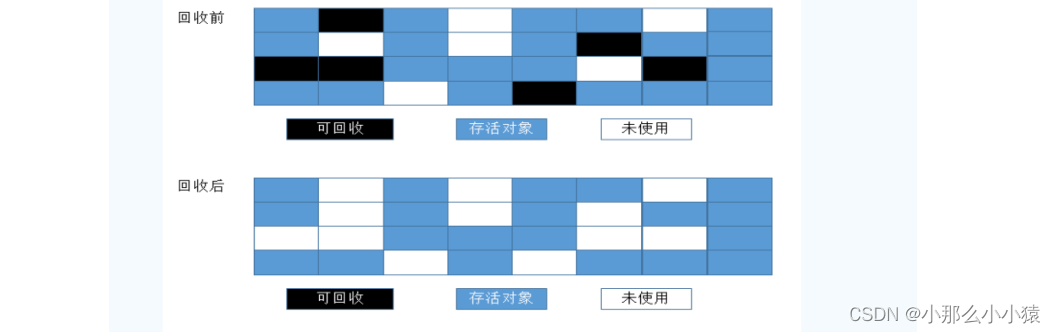
JVM垃圾回收机制GC理解
目录JVM垃圾回收分代收集如何识别垃圾引用计数法可达性分析法引用关系四种类型: 强、软、弱、虚强引用软引用 SoftReference弱引用 WeakReferenceWeakHashMap软引用与虚引用的使用场景虚引用与引用队列引用队列虚引用 PhantomReference垃圾回收算法引用计数复制 Cop…...

C++中的容器
1.1 线性容器1)std::array看到这个容器的时候肯定会出现这样的问题:为什么要引入 std::array 而不是直接使用 std::vector?已经有了传统数组,为什么要用 std::array?先回答第一个问题,与 std::vector 不同,…...
2023备战金三银四,Python自动化软件测试面试宝典合集(五)
接上篇八、抓包与网络协议8.1 抓包工具怎么用 我原来的公司对于抓包这块,在 App 的测试用得比较多。我们会使用 fiddler 抓取数据检查结果,定位问题,测试安全,制造弱网环境;如:抓取数据通过查看请求数据,请…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...
