代码随想录算法训练营|day48
第九章 动态规划
- 121.买卖股票的最佳时机
- 122.买卖股票的最佳时机II
- 代码随想录文章详解
121.买卖股票的最佳时机
本题中股票只能买卖一次
dp[i][0] 表示第i天不买入股票持有的最大现金;dp[i][1] 表示第i天买入股票持有的最大现金。
| 不买股票持有的最大现金 | 买入股票持有的最大现金 |
|---|---|
前一天为未买入状态 dp[i-1][0]前一天为买入状态,今天卖出 dp[i-1][1]+prices[i] | 前一天为买入状态 dp[i-1][1]今天为买入状态 -prices[i] |
func maxProfit(prices []int) int {if len(prices) == 0 {return 0}dp := make([][]int, len(prices))for i := 0; i < len(prices); i++ {dp[i] = make([]int, 2)}dp[0][0] = 0dp[0][1] = -prices[0]for i := 1; i < len(prices); i++ {dp[i][0] = max(dp[i-1][0], dp[i-1][1]+prices[i])dp[i][1] = max(dp[i-1][1], -prices[i])}return dp[len(prices) - 1][0]
}
空间优化:可以看到第i天状态只依赖于第i-1天的状态,因此只需要记录前一天状态即可
func maxProfit(prices []int) int {if len(prices) == 0 {return 0}dp0, dp1 := 0, -prices[0]for i := 1; i < len(prices); i++ {dp0 = max(dp0, dp1+prices[i])dp1 = max(dp1, -prices[i])}return dp0
}
贪心:在历史最低点买入,最高点卖出
func maxProfit(prices []int) int {if len(prices) == 0 {return 0}minPrice := prices[0]res := 0for i := 1; i < len(prices); i++ {if prices[i] < minPrice {minPrice = prices[i]}res = max(res, prices[i]-minPrice)}return res
}
122.买卖股票的最佳时机II
较上题多了条件:股票可以进行多次买卖
dp[i][0] 表示第i天不买入股票持有的最大现金;dp[i][1] 表示第i天买入股票持有的最大现金。
所以在当天是买入状态时,持有的最大现金为前一天买入状态持有的最大现金和前一天卖出今天买入后持有的最大现金的最大值
func maxProfit(prices []int) int {if len(prices) == 0 || len(prices) == 1 {return 0}dp := make([][]int, len(prices))for i := 0; i < len(prices); i++ {dp[i] = make([]int, 2)}dp[0][0] = 0dp[0][1] = -prices[0]for i := 1; i < len(prices); i++ {dp[i][0] = max(dp[i-1][0], dp[i-1][1]+prices[i])dp[i][1] = max(dp[i-1][1], dp[i-1][0]-prices[i])}return dp[len(prices)-1][0]
}
空间优化
func maxProfit(prices []int) int {if len(prices) == 0 || len(prices) == 1 {return 0}dp0, dp1 := 0, -prices[0]for i := 0; i < len(prices); i++ {dp0 = max(dp0, dp1+prices[i])dp1 = max(dp1, dp0-prices[i])}return dp0
}
贪心:只加正数
因为不限制交易次数,故只要今天股价比昨天高,就交易。
func maxProfit(prices []int) int {if len(prices) == 0 || len(prices) == 1 {return 0}sum := 0for i := 1; i < len(prices); i++ {if prices[i] > prices[i-1] {sum += prices[i] - prices[i-1]}}return sum
}代码随想录文章详解
121.买卖股票的最佳时机
122.买卖股票的最佳时机II
相关文章:

代码随想录算法训练营|day48
第九章 动态规划 121.买卖股票的最佳时机122.买卖股票的最佳时机II代码随想录文章详解 121.买卖股票的最佳时机 本题中股票只能买卖一次 dp[i][0] 表示第i天不买入股票持有的最大现金;dp[i][1] 表示第i天买入股票持有的最大现金。 不买股票持有的最大现金买入股票…...
)
架构面试题汇总:并发和锁(三)
在现代软件开发中,并发编程和多线程处理已成为不可或缺的技能。Java作为一种广泛使用的编程语言,提供了丰富的并发和多线程工具,如锁、同步器、并发容器等。因此,对于Java开发者来说,掌握并发编程和多线程处理的知识至…...

蓝桥杯(3.2)
1209. 带分数 import java.io.*;public class Main {static BufferedReader br new BufferedReader(new InputStreamReader(System.in));static PrintWriter pw new PrintWriter(new OutputStreamWriter(System.out));static final int N 10;static int n, cnt;static int[…...

[数据集][目标检测]鸟类检测数据集VOC+YOLO格式11758张200类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):11758 标注数量(xml文件个数):11758 标注数量(txt文件个数):11758 标…...
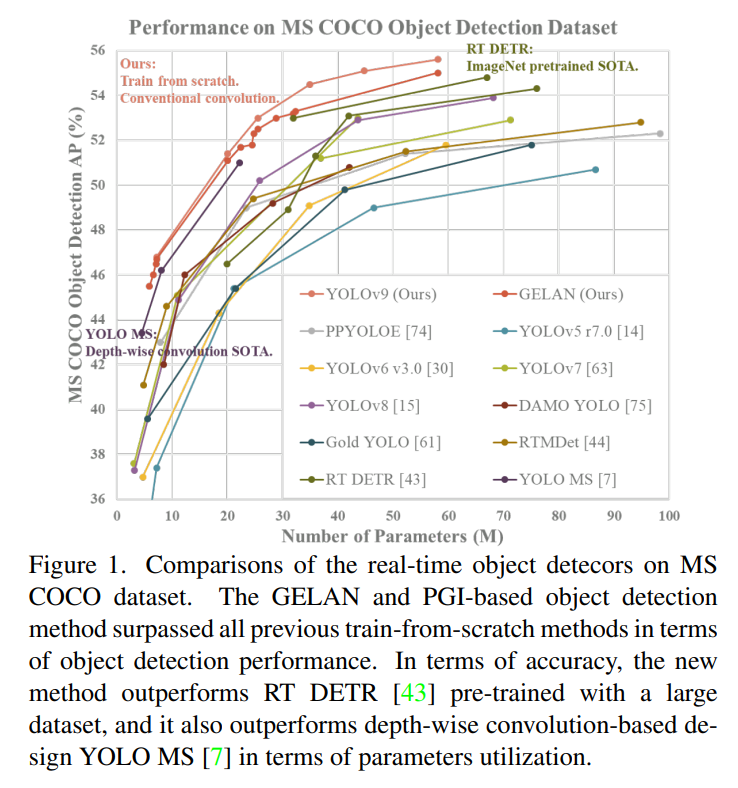
YOLOv9:使用可编程梯度信息学习您想学习的内容
摘要 arxiv.org/pdf/2402.13616.pdf 当今的深度学习方法侧重于如何设计最合适的目标函数,以便模型的预测结果能最接近于实际结果。同时,还必须设计一个适当的架构,以便于获取足够的预测信息。现有的方法忽略了一个事实,即当输入数据经历层层特征提取和空间变换时,会损失…...
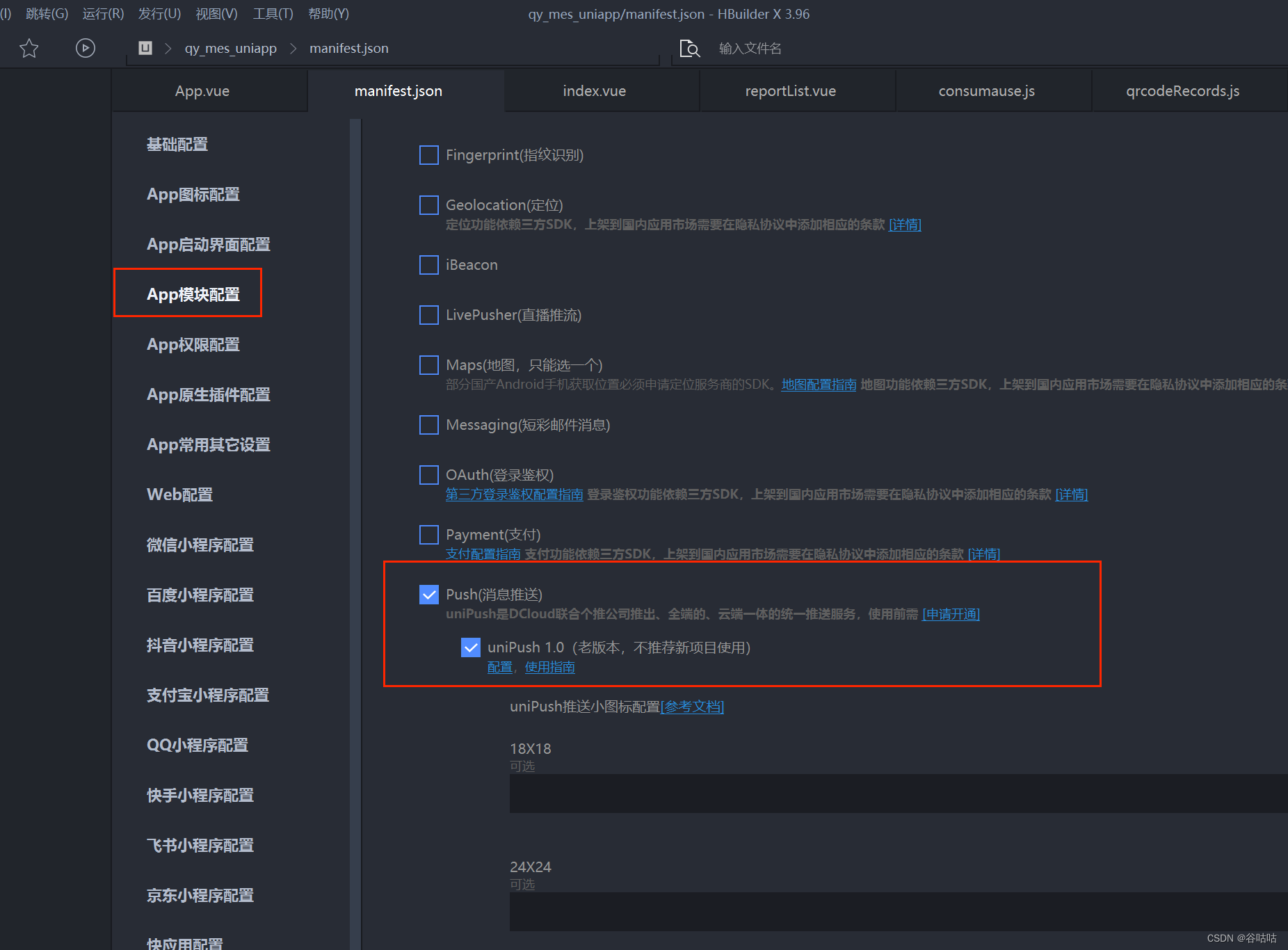
uniapp:使用DCloud的uni-push推送消息通知(在线模式)java实现
uniapp:使用DCloud的uni-push推送消息通知(在线模式)java实现 1.背景 今天开发app的时候遇到一个需求: 业务在出发特定条件的时候向对应的客户端推送消息通知。 为什么选择在线模式,因为我们使用的是德邦类似的手持终端…...

【简说八股】面试官:你知道什么是AOP么?
回答 AOP(Aspect-Oriented Programming),即面向切面编程,是一种编程范式,它的主要思想是将应用程序中的横切关注点(如日志记录、性能统计、安全控制等)从业务逻辑中剥离出来,然后通过特殊的方式将这些横切…...
ASUS华硕天选5笔记本电脑FX607JV原装出厂Win11系统下载
ASUS TUF Gaming F16 FX607JV天选五原厂Windows11系统 适用型号: FX607JU、FX607JI、FX607JV、 FX607JIR、FX607JVR、FX607JUR 下载链接:https://pan.baidu.com/s/1l963wqxT0q1Idr98ACzynQ?pwd0d46 提取码:0d46 原厂系统自带所有驱动、…...
Unity(第二十一部)动画的基础了解(感觉不了解其实也行)
1、动画组件老的是Animations 动画视频Play Automatically 是否自动播放Animate Physics 驱动方式,勾选后是物理驱动Culling Type 剔除方式 默认总是动画化就会一直执行下去,第二个是基于渲染播放(离开镜头后不执行), …...
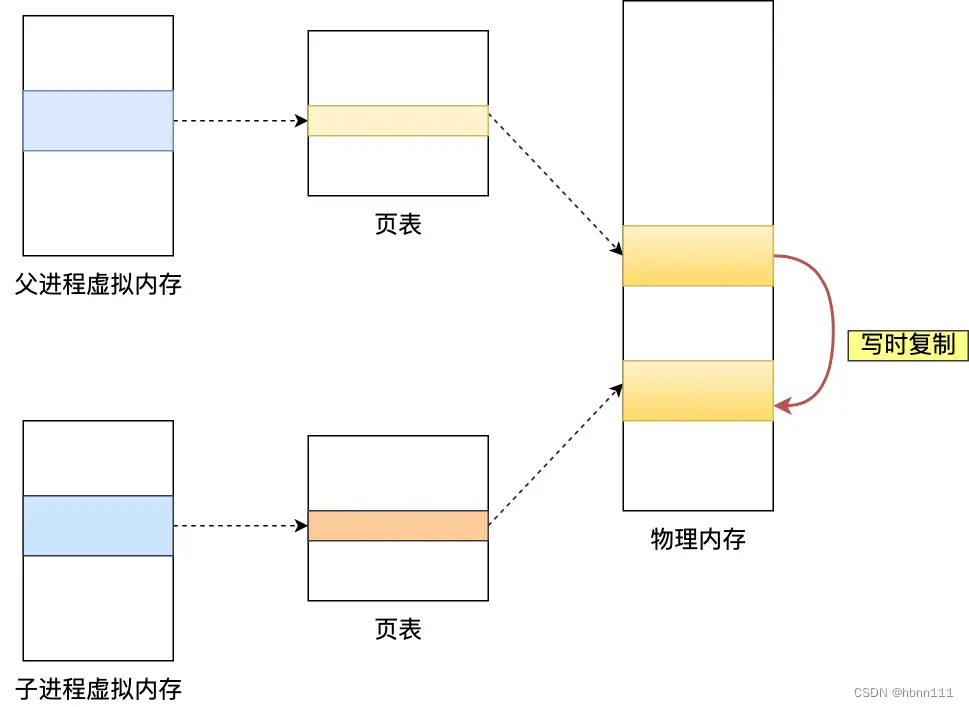
写时复制简介
写时复制技术(Copy on Write)是比较常用的一种技术,它的主要目的是延迟减少以及延迟内存的分配,增加执行效率,只有在真正进行写操作的过程中才会真正分配物理资源。同时,也可以保护数据在系统崩溃时出现的丢失。比如,我…...

运行Python文件时出现‘utf-8’code can‘t decode byte 如何解决?(如图)
如图 亦或者出现“SyntaxError: Non-UTF-8 code starting with \xbb ” 出现这种问题往往是编码格式导致的,我们可以在py文件中的第一行加入以下代码: # codingutf-8或者 # codinggdk优先使用gbk编码 解释一下常用的两种编码格式: utf-…...
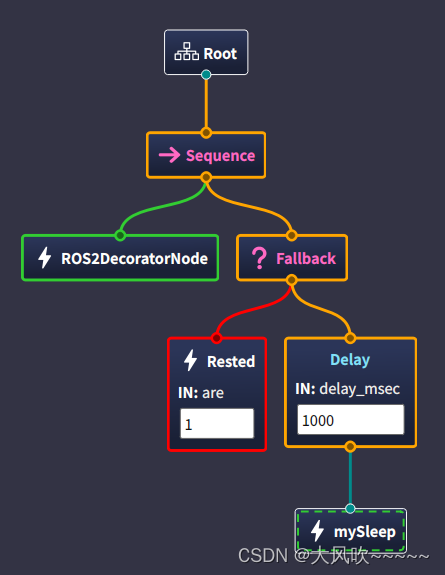
行为树入门:BehaviorTree.CPP Groot2练习(叶子节点)(2)
以《行为树BehaviorTree学习记录1_基本概念》练习。 1 SequenceNode顺序控制节点 代码下载 git clone https://gitee.com/Luweizhiyuan2020/ros2_bt.git例程 1.1 sequence 顺序执行 下载版本SequenceNode1。 1.2 ReactiveSequence 异步执行 注意: ①only a…...

leetcode-字符串中的单词数
434. 字符串中的单词数 题解: 这个问题可以通过遍历字符串,当遇到非空格字符时,判断其前一个字符是否为空格,如果是,则说明这是一个新的单词的开始,计数器加一。最后返回计数器的值即可。 class Solutio…...

一些C语言题目
求10个整数中最大值 #include <stdio.h>//求10个整数中最大值 int main() {int arr[10]{2,5,8,6,19,1,7,3,11,3};int i 0;int max 0;/*for(i 0;i < 10;i){scanf("%d",&arr[i]);}*/for(i 0;i < 10;i){if(arr[i] > max)max arr[i];}printf(&q…...
JVM相关问题
JVM相关问题 一、Java继承时父子类的初始化顺序是怎样的?二、JVM类加载的双亲委派模型?三、JDK为什么要设计双亲委派模型,有什么好处?四、可以打破JVM双亲委派模型吗?如何打破JVM双亲委派模型?五、什么是内…...
32单片机基础:旋转编码器计次
接线图如上图所示。 我们初始化一下PB0和PB1两个GPIO口外设中断,当然,这里只初始化一个外部中断也能完成功能的对于编码器而言,下图所示为正转的波形。如果把一相的下降沿用作触发中断,在中断时刻读取另一相的电平,正…...
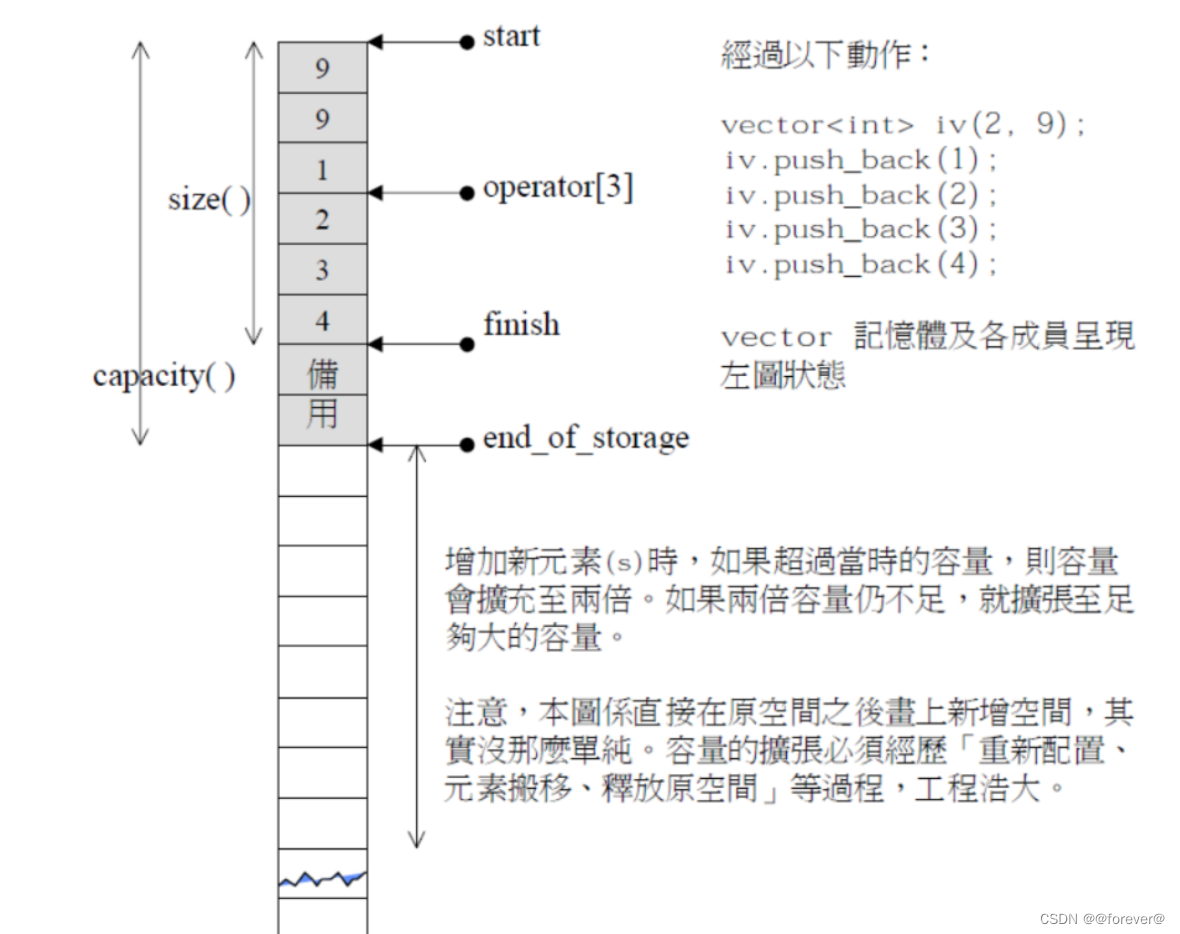
【C++】vector的使用和模拟实现(超级详解!!!!)
文章目录 前言1.vector的介绍及使用1.1 vector的介绍1.2 vector的使用1.2.1 vector的定义1.2.2 vector iterator 的使用1.2.3 vector 空间增长问题1.2.3 vector 增删查改1.2.4 vector 迭代器失效问题。(重点!!!!!!)1.2.5 vector 在OJ中有关的练习题 2.ve…...

GO学习记录
这里写目录标题 00 环境01 语言基础二级目录三级目录 00 环境 参考的:https://www.liwenzhou.com/posts/Go/install/ 编译运行: go mod init <项目名> // 在目录下创建项目 go mod init <项目名> // 编译go run <文件名>.go …...
)
迭代器模式(Iterator Pattern)
定义 迭代器模式(Iterator Pattern)是一种行为型设计模式,它提供了一种方法来顺序访问聚合对象中的各个元素,而不需要暴露该对象的内部表示。迭代器模式使得客户端代码能够独立于聚合对象的具体实现进行遍历操作。 在迭代器模式…...
详解)
KL divergence(KL 散度)详解
本文用一种浅显易懂的方式说明KL散度。 参考资料 KL散度本质上是比较两个分布的相似程度。 现在给出2个简单的离散分布,称为分布1和分布2. 分布1有3个样本, 其中A的概率为50%, B的概率为40%,C的概率为10% 分布2也有3个样本: 其…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...
