在Redhat 7 Linux上安装llama.cpp [ 错误stdatomic.h: No such file or directory]
前期准备
在github上下载llama.cpp或克隆。
GitHub - ggerganov/llama.cpp: LLM inference in C/C++
git clone https://github.com/ggerganov/llama.cpp.gitcd llama.cpp执行make命令编译llama.cpp
make在huggingface里下载量化了的 gguf格式的llama2模型。
https://huggingface.co/TheBloke/Llama-2-7B-Chat-GGUF/tree/main
我下载的是llama-2-7b-chat.Q4_0.gguf
拷贝llama-2-7b-chat.Q4_0.gguf 到llama.cpp目录里的models目录里
正常安装的错误信息
安装 gcc 和gcc-c++ 之后,你运行Make 命令编译llama.cpp的时候,你会发现下面问题。
yum -y install gcc --nogpgcheckyum -y install gcc-c++ --nogpgcheck错误信息, 因为gcc 的版本是4.8
cc -I. -Icommon -D_XOPEN_SOURCE=600 -D_GNU_SOURCE -DNDEBUG -std=c11 -fPIC -O3 -Wall -Wextra -Wpedantic -Wcast-qual -Wno-unused-function -Wshadow -Wstrict-prototypes -Wpointer-arith -Wmissing-prototypes -Werror=implicit-int -Werror=implicit-function-declaration -pthread -march=native -mtune=native -Wdouble-promotion -c ggml.c -o ggml.oggml.c:92:23: fatal error: stdatomic.h: No such file or directory#include <stdatomic.h>^compilation terminated.make: *** [ggml.o] Error 1解决方法
1. 从下面连接下载 gcc-12.2.0
Index of /gnu/gcc/releases/gcc-12.2.0
2. 解压下载的gcc-12.2.0.tar.gz
tar xvf gcc-12.2.0.tar.gz3. 用root权限运行下面命令
yum -y install gmp-devel mpfr-devel libmpc-devel --nogpgcheck4. 运行下面命令安装gcc 12.2.0 版本
cd gcc-12.2.0./configure --disable-multilib --enable-languages=c,c++# change -j <cores_num> if you have more cpu cores for building be fastermake -j 4make installgcc --versionexport CC=gccexport LD_LIBRARY_PATH=/usr/local/lib:/usr/lib:/usr/local/lib64:/usr/lib645. 下载和编译llama.cpp
git clone https://github.com/ggerganov/llama.cpp.gitcd llama.cppmake
或者直接下载后运行make命令
GitHub - ggerganov/llama.cpp at llama_server_completions
6. 运行llama.cpp
./main -m ./models/llama-2-7b-chat.Q4_0.gguf --color --ctx_size 2048 -n -1 -ins -b 256 --top_k 10000 --temp 0.2 --repeat_penalty 1.1 -t 8在Redhat 8安装
在redhat8 上直接安装gcc, gcc-c++ , 然后编译llama.cpp就可以了
yum -y install make --nogpgcheck
yum -y install gcc --nogpgcheck
yum -y install gcc-c++ --nogpgcheck其它llama2的系列博客
在Windows或Mac上安装并运行LLAMA2
相关文章:

在Redhat 7 Linux上安装llama.cpp [ 错误stdatomic.h: No such file or directory]
前期准备 在github上下载llama.cpp或克隆。 GitHub - ggerganov/llama.cpp: LLM inference in C/C git clone https://github.com/ggerganov/llama.cpp.gitcd llama.cpp 执行make命令编译llama.cpp make 在huggingface里下载量化了的 gguf格式的llama2模型。 https:/…...

linux 常用 命令行HTTP客户端
在Linux环境中,命令行HTTP客户端是一种用于发送HTTP请求的工具,它们通常用于测试网站、服务器或API的响应。这些客户端支持各种HTTP方法,如GET、POST、PUT、DELETE等,并允许用户设置请求头、发送数据等。以下是一些常用的命令行HT…...

深入理解@Param注解:用于参数映射的利器
摘要:Param注解在Java开发中被广泛应用,它可以优雅地解决方法参数与SQL语句中占位符的映射问题,提高代码的可读性和可维护性。本文将深入探讨Param注解的背景、使用方法、解决的问题、映射原理,并对使用与不使用Param注解的情况进…...

OCP Secure boot必要特性
三点必需要求: The platform components must: 1. Provide a mechanism for securely anchoring a root of trust public key. // 提供一种用于安全地锚定信任根公钥的机制。 2. Verify the device firmware digital signature using the anchored public key /…...
全新攻击面管理平台
首页大屏 内测阶段,免费试用一个月 有兴趣体验的师傅,来长亭云图极速版群里找我 py...

在VMware中安装CentOS 7并配置Docker
VMware安装CentOS 7 一、介绍 该文章介绍如何使用启动U盘在虚拟机里面安装系统,虚拟机版本为VMware Workstation 16 pro,Linux版本为CentOS Linux release 7.9.2009 (Core)。 二、安装 1、创建虚拟机 点击创建新的虚拟机 选择典型就可以了…...
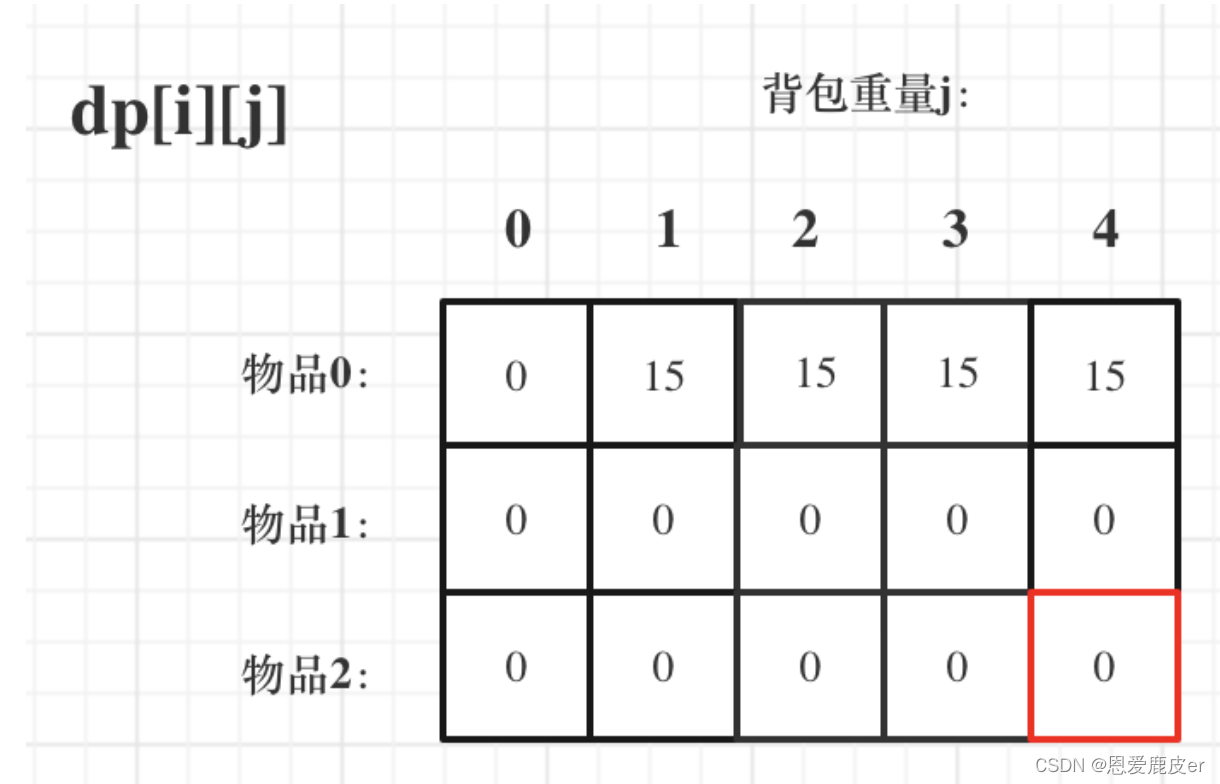
Leetcoder Day37| 动态规划part04 背包问题
01背包理论基础 面试掌握01背包,完全背包和重背包就够用了。 背包问题的理论基础重中之重是01背包,一定要理解透! 01 背包 有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品…...
)
突破编程_C++_面试(STL 编程 vector )
面试题 1 :std::vector 的底层存储机制是什么? std::vector 的底层存储机制是一个动态数组,它内部通过一片连续的内存空间来存储元素。当这个连续的内存空间不足以容纳新元素时,std::vector 会自动申请一块更大的内存空间&#x…...
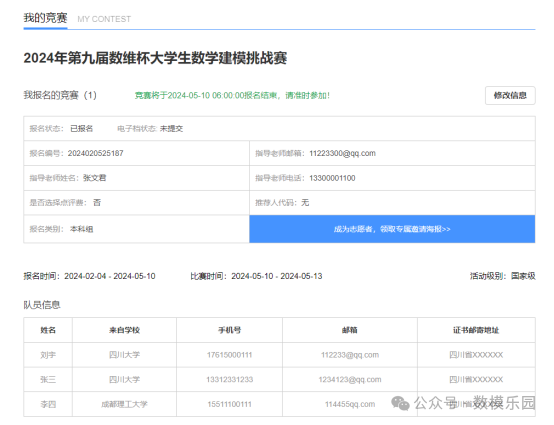
【报名指南】2024年第九届数维杯数学建模挑战赛报名全流程图解
1.官方报名链接: 2024年第九届数维杯大学生数学建模挑战赛http://www.nmmcm.org.cn/match_detail/32 2.报名流程(电脑与手机报名操作流程一致) 参赛对象为在校专科生、本科生、研究生,每组参赛人数为1-3人(指导老师不…...
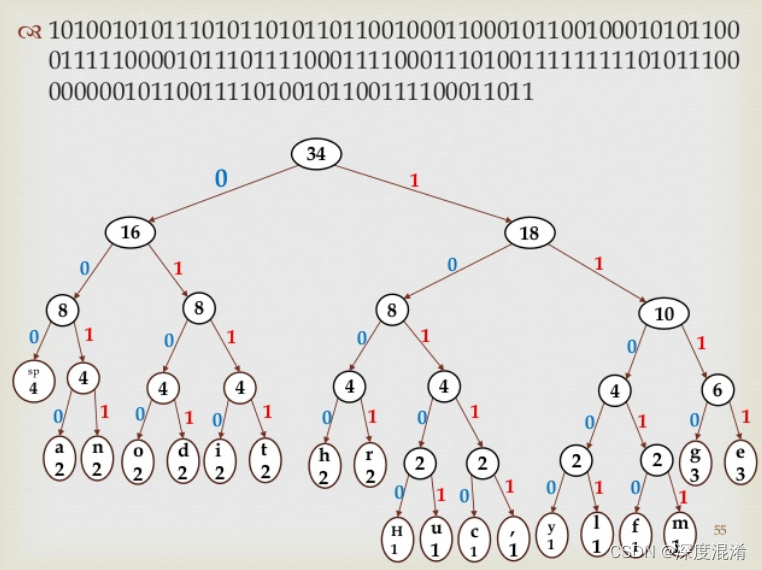
C#,哈夫曼编码(Huffman Code)压缩(Compress )与解压缩(Decompress)算法与源代码
David A. Huffman 1 哈夫曼编码简史(Huffman code) 1951年,哈夫曼和他在MIT信息论的同学需要选择是完成学期报告还是期末考试。导师Robert M. Fano给他们的学期报告的题目是,寻找最有效的二进制编码。由于无法证明哪个已有编码是…...
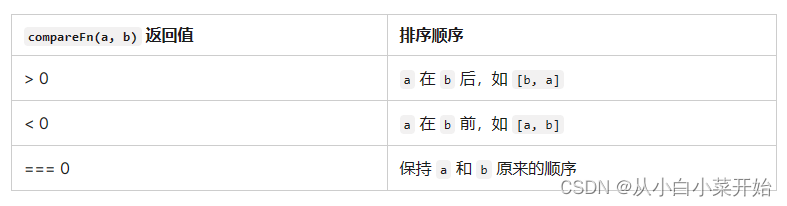
JS 对象数组排序方法测试
输出 一.Array.prototype.sort() 1.默认排序 sort() sort() 方法就地对数组的元素进行排序,并返回对相同数组的引用。默认排序是将元素转换为字符串,然后按照它们的 UTF-16 码元值升序排序。 由于它取决于具体实现,因此无法保证排序的时…...

【计算机考研】408学到什么程度才能考130?
408考130要比考研数学考130难的多 我想大部分考过408的考生都是这么认为的。408的难点在于他涉及的范围太广了,首先如果你要备考408,你要准备四门课程,分别是数据结构,计算机组成原理,操作系统和计算机网络。 这四门…...

“智农”-农业物联网可视化
大棚可视化|设施农业可视化|农业元宇宙|农业数字孪生|大棚物联网|大棚数字孪生|农业一体化管控平台|智慧农业可视化|智农|农业物联网可视化|农业物联网数字孪生|智慧农业|大棚三维可视化|智慧大棚可视化|智慧大棚|农业智慧园区|数字农业|数字大棚|农业大脑|智慧牧业数字孪生|智…...

day03-网络编程
1>TCP机械臂测试 #include<myhead.h> #define SER_IP "10.211.55.11" #define SER_PORT 8888 #define CLI_IP "10.211.55.9" #define CLI_PORT 6666 //客户端 int main(int argc, const char *argv[]) {//1、创建用于通信的套接字文件描述符int …...

Java反射,动态代理。笔记
1.pathClass Loader 和 Dex ClassLoader 在Android 5.0以下的版本中,两者之间的区别为: DexClassLoader:可加载jar、apk和dex」可以从SD卡中加载PathClassLoader:只能加载已安裝到系統中(即/data/app目录下)的apk文件但是随着Android版本的升级,到Android …...

作为团队开发组长你需要做的:
当你需要开始团队开发时,以下是一些你可能需要知道和使用的工具、实践和原则: 1. 版本控制系统 (VCS): 使用版本控制系统(如Git)来管理代码。这能确保团队成员协同工作时能够跟踪和管理代码的变更。创建分支进行开发,…...
)
Windows安装Neo4j数据库教程(3.X版本)
安装java的jdk(jdk1.8仅支持Neo4j 3.X版本)去 Index of /doc/neo4j/ 下载目标版本的Windows zip安装包将安装包解压到任意目录,并记住解压后带版本号的文件夹路径添加系统环境变量,变量名:NEO4J_HOME,变量值…...

无人机飞行控制系统技术,四旋翼无人机控制系统建模技术详解
物理建模是四旋翼无人机控制系统建模的基础,主要涉及到无人机的物理特性和运动学特性。物理建模的目的是将无人机的运动与输入信号(如控制电压)之间的关系进行数学描述。 四旋翼无人直升机是具有四个输入力和六个坐标输出的欠驱动动力学旋翼…...

程序员的金三银四求职宝典:如何在关键时期脱颖而出?
个人主页:17_Kevin-CSDN博客 随着春天的脚步渐近,程序员们的求职热潮也随之而来。在这个被称为“金三银四”的招聘季,如何从众多求职者中脱颖而出,成为了许多程序员关注的焦点。本文将为你提供一份全面的求职宝典,助你…...

分享经典、现代和前沿软件工程课程
随着信息技术的发展,软件已经深入到人类社会生产和生活的各个方面。软件工程是将工程化的方法运用到软件的开发、运行和维护之中,以达到提高软件质量,降低开发成本的目的。软件工程已经成为当今最活跃、最热门的学科之一。 本次软件工程MOOC课…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...
