Leetcoder Day37| 动态规划part04 背包问题
01背包理论基础
面试掌握01背包,完全背包和重背包就够用了。
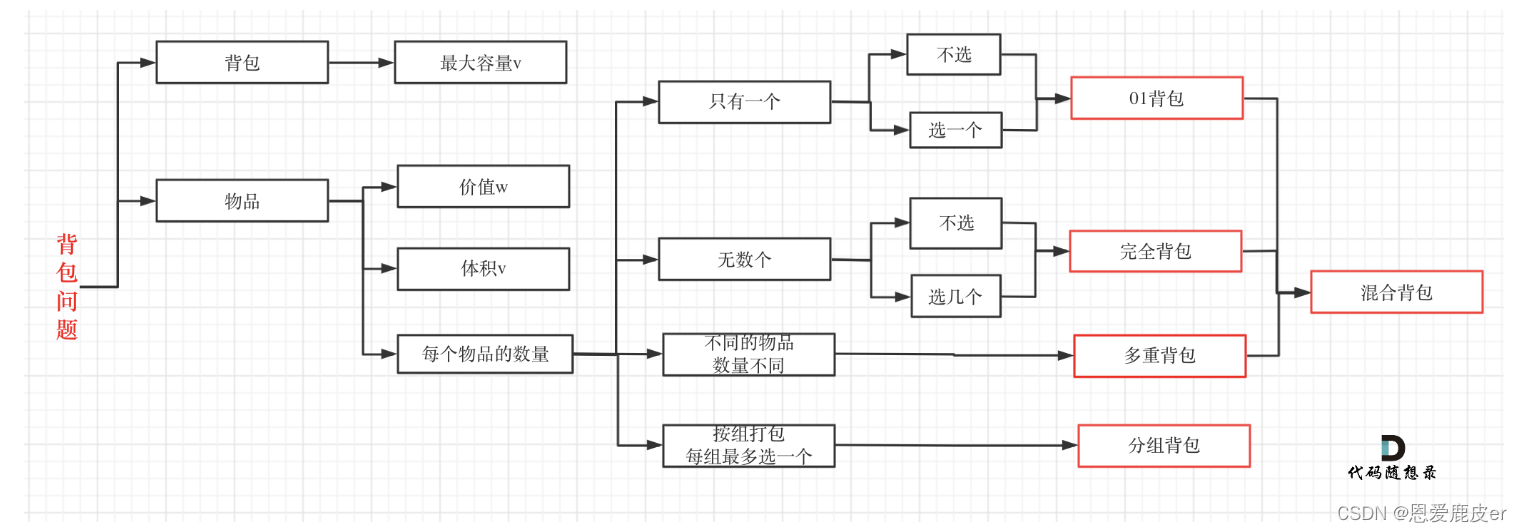
背包问题的理论基础重中之重是01背包,一定要理解透!
01 背包
有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
每一件物品其实只有两个状态,取或者不取,所以可以使用回溯法搜索出所有的情况,那么时间复杂度就是o(2^n),这里的n表示物品数量。
所以暴力的解法是指数级别的时间复杂度。进而才需要动态规划的解法来进行优化!
举例:背包最大重量为4。
物品为:
| 重量 | 价值 | |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
问背包能背的物品最大价值是多少?
以下讲解和图示中出现的数字都是以这个例子为例。
二维数组01背包
依然动规五部曲分析一波。
1. 确定dp数组以及下标的含义
对于背包问题,有一种写法, 是使用二维数组,即dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。要时刻记着这个dp数组的含义,下面的一些步骤都围绕这dp数组的含义进行的。
2. 确定递推公式
有两个方向可以推出来dp[i][j],
- 不放物品i:由dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量或背包剩余重量小于i的重量时,物品i无法放进背包中,所以背包内的价值依然和前面相同。)
- 放物品i:由dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值,那么dp[i - 1][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值。
所以dp[i][j]= max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])
3. dp数组如何初始化
关于初始化,一定要和dp数组的定义吻合,否则到递推公式的时候就会越来越乱。
首先从dp[i][j]的定义出发,如果背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0。i是由i-1推出来的,所以i为0的时候就一定要初始化。刚才讨论过j=0的情况,那么i=0时,dp[0][j],即:存放编号0的物品时,各个容量的背包所能存放的最大价值。因此 j < weight[0]时,dp[0][j] 应该是 0,因为背包容量比编号0的物品重量还小。若j>=weight[0],dp[0][j]的值为value[0]。
dp[0][j] 和 dp[i][0] 初始化以后,其他位置都会从i-1或者j-weight[i]而来,因此都会被不断地覆盖,所以初始化为0即可。
4. 确定遍历顺序
在如下图中,可以看出,有两个遍历的维度:物品与背包重量,从哪个方向遍历都可以,因此我们就从物品开始遍历。
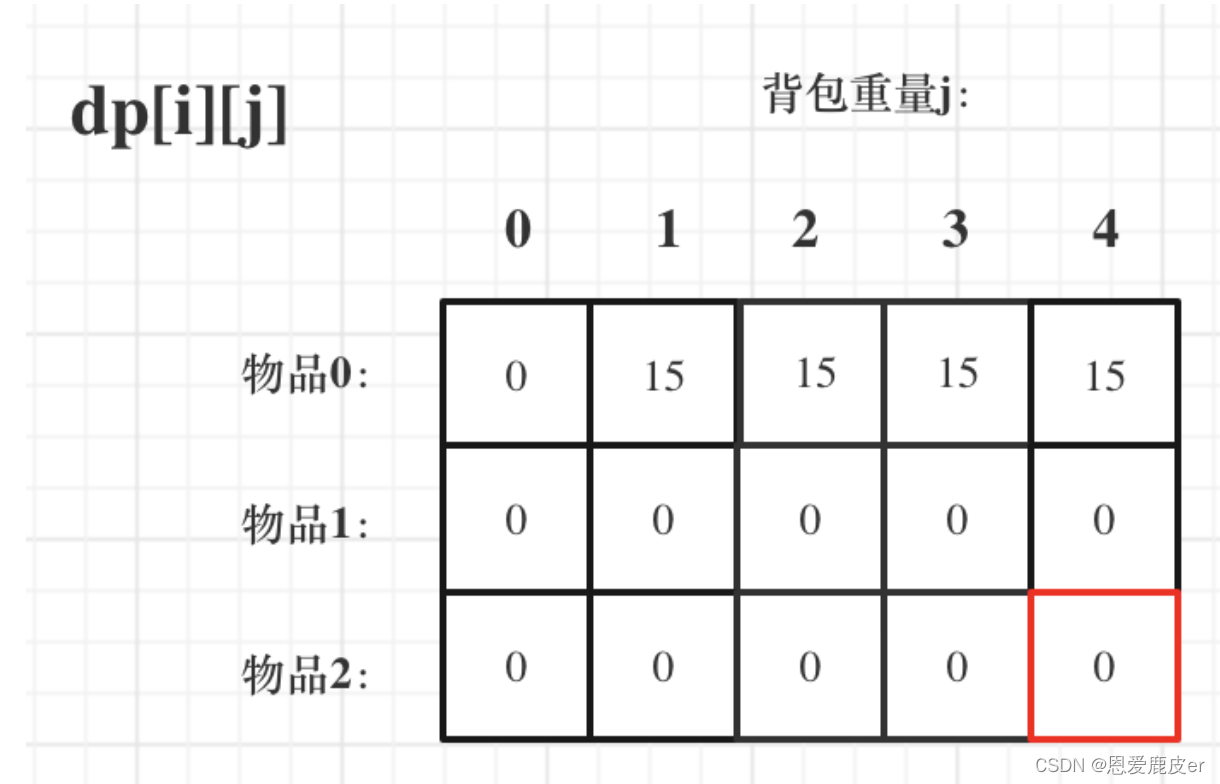
public static void backValue(int[]value, int[] weight, int bagWeight){int num=value.length;int[][]dp=new int[num][bagWeight+1];for(int j=weight[0];j<bagWeight;j++){dp[0][j]=value[0];}for(int i=1;i<num;i++){//从物品开始遍历for(int j=1;j<=bagWeight;j++){if(j<weight[i]) dp[i][j]=dp[i-1][j];else{dp[i][j] = Math.max(dp[i-1][j] , dp[i-1][j-weight[i]] + value[i]);}}}System.out.println(dp[num-1][bagWeight]);} 一维数组01背包
上面的思路是用二维数组来解决01背包问题,还可以用滚动数组来解决,即把二维dp降维。
在使用二维数组的时候,递推公式:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
其实可以发现如果把dp[i - 1]那一层拷贝到dp[i]上,表达式完全可以是:dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);
与其把dp[i - 1]这一层拷贝到dp[i]上,不如只用一个一维数组了,只用dp[j](一维数组,也可以理解是一个滚动数组)。
因此,动规五部曲分析如下:
1. 确定dp数组的定义
在一维dp数组中,dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]。
2. 一维dp数组的递推公式
dp[j]为 容量为j的背包所背的最大价值,那么如何推导dp[j]呢?
dp[j]可以通过dp[j - weight[i]]推导出来,dp[j - weight[i]]表示容量为j - weight[i]的背包所背的最大价值。
dp[j - weight[i]] + value[i] 表示 容量为 j - 物品i重量 的背包 加上 物品i的价值。(也就是容量为j的背包,放入物品i了之后的价值即:dp[j])
此时dp[j]有两个选择,一个是取自己dp[j] 相当于 二维dp数组中的dp[i-1][j],即不放物品i,一个是取dp[j - weight[i]] + value[i],即放物品i,指定是取最大的,毕竟是求最大价值。
所以递推公式为:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
3. 一维dp数组如何初始化
dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j],那么dp[0]就应该是0,因为背包容量为0所背的物品的最大价值就是0。
那么dp数组除了下标0的位置,初始为0,其他下标应该初始化多少呢?
看一下递归公式:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
dp数组在推导的时候一定是取价值最大的数,如果题目给的价值都是正整数那么非0下标都初始化为0就可以了。
这样才能让dp数组在递归公式的过程中取的最大的价值,而不是被初始值覆盖了。
那么我假设物品价值都是大于0的,所以dp数组初始化的时候,都初始为0就可以了。
4. 一维dp数组遍历顺序
二维dp遍历的时候,背包容量是从小到大,而一维dp遍历的时候,背包是从大到小。
因为倒序遍历是为了保证物品i只被放入一次!。但如果一旦正序遍历了,那么物品0就会被重复加入多次!
举一个例子:物品0的重量weight[0] = 1,价值value[0] = 15
如果正序遍历
dp[1] = dp[1 - weight[0]] + value[0] = 15
dp[2] = dp[2 - weight[0]] + value[0] = 30
此时dp[2]就已经是30了,意味着物品0,被放入了两次,所以不能正序遍历。
为什么倒序遍历,就可以保证物品只放入一次呢?
倒序就是先算dp[2]
dp[2] = dp[2 - weight[0]] + value[0] = 15 (dp数组已经都初始化为0)
dp[1] = dp[1 - weight[0]] + value[0] = 15
所以从后往前循环,每次取得状态不会和之前取得状态重合,这样每种物品就只取一次了。
为什么二维dp数组遍历的时候不用倒序呢?
因为对于二维dp,dp[i][j]都是通过上一层即dp[i - 1][j]计算而来,本层的dp[i][j]并不会被覆盖!
先遍历物品嵌套遍历背包容量,那可不可以先遍历背包容量嵌套遍历物品呢?不可以!
因为一维dp的写法,背包容量一定是要倒序遍历(原因上面已经讲了),如果遍历背包容量放在上一层,那么每个dp[j]就只会放入一个物品,即:背包里只放入了一个物品。
倒序遍历的原因是,本质上还是一个对二维数组的遍历,并且右下角的值依赖上一层左上角的值,因此需要保证左边的值仍然是上一层的,从右向左覆盖。
⚠️一维和二维的区别:(1)一维到序遍历,二维正序遍历(2)一维只能先遍历物品再遍历背包,但是二维两个顺序都可。
public static void getBackValue(int[]value, int[] weight, int bagWeight){int num=value.length;int[]dp=new int[bagWeight+1];for(int j=weight[0];j<bagWeight;j++){dp[j]=value[0];}for(int i=1;i<num;i++){//从物品开始遍历for(int j=bagWeight;j>=weight[i];j--){//要倒序遍历dp[j]=Math.max(dp[j], dp[j-weight[i]]+value[i]);}}System.out.println(dp[bagWeight]);} 416. 分割等和子集
给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
注意: 每个数组中的元素不会超过 100 数组的大小不会超过 200
示例 1:
- 输入: [1, 5, 11, 5]
- 输出: true
- 解释: 数组可以分割成 [1, 5, 5] 和 [11].
示例 2:
- 输入: [1, 2, 3, 5]
- 输出: false
- 解释: 数组不能分割成两个元素和相等的子集.
提示:
- 1 <= nums.length <= 200
- 1 <= nums[i] <= 100
这道题希望能够将一个数组拆成两个子集a和b,使得a里面的元素和等于b里面的元素和。
没有什么思路,直接看了代码随想录。原来是01背包问题的变种。
01背包问题:有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
注意题目描述中商品是不是可以重复放入。一个商品如果可以重复多次放入是完全背包,而只能放入一次是01背包。
要明确本题中我们要使用的是01背包,因为元素我们只能用一次。
回归主题:首先,本题要求集合里能否出现总和为 sum / 2 的子集。(这一点是我没有想到的)
那么来一一对应一下本题,看看背包问题如何来解决。
只有确定了如下四点,才能把01背包问题套到本题上来:
- 背包的可容纳的重量为sum / 2
- 背包要放入的商品(集合里的元素)重量为元素的数值,价值也为元素的数值
- 背包如果正好装满,说明找到了总和为 sum / 2 的子集。
- 背包中每一个元素是不可重复放入
dp[j]表示:背包总容量是j,放进物品后,背包的最大价值为dp[j]。
那么如果背包需要满足的容量为target,当dp[target]==target时,背包就装满了
class Solution {/**背包的可容纳的重量为sum / 2背包要放入的商品(集合里的元素)重量为元素的数值,价值也为元素的数值背包如果正好装满,说明找到了总和为 sum / 2 的子集。背包中每一个元素是不可重复放入*/public boolean canPartition(int[] nums) {int sum=0;for(int i=0;i<nums.length;i++){sum+=nums[i];}if(sum%2==1) return false;int target=sum/2;//weight[i]和value[i]都是nums[i],当前的bacWeight为targetint[] dp=new int[target+1];for(int j=nums[0];j<target;j++){dp[j]=nums[0];}for(int i=1;i<nums.length;i++){ //先遍历物品for(int j=target;j>=nums[i];j--){//重量要倒序遍历dp[j]=Math.max(dp[j], dp[j-nums[i]]+nums[i]);}}if(dp[target]==target) return true;return false;}
}相关文章:

Leetcoder Day37| 动态规划part04 背包问题
01背包理论基础 面试掌握01背包,完全背包和重背包就够用了。 背包问题的理论基础重中之重是01背包,一定要理解透! 01 背包 有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品…...
)
突破编程_C++_面试(STL 编程 vector )
面试题 1 :std::vector 的底层存储机制是什么? std::vector 的底层存储机制是一个动态数组,它内部通过一片连续的内存空间来存储元素。当这个连续的内存空间不足以容纳新元素时,std::vector 会自动申请一块更大的内存空间&#x…...
【报名指南】2024年第九届数维杯数学建模挑战赛报名全流程图解
1.官方报名链接: 2024年第九届数维杯大学生数学建模挑战赛http://www.nmmcm.org.cn/match_detail/32 2.报名流程(电脑与手机报名操作流程一致) 参赛对象为在校专科生、本科生、研究生,每组参赛人数为1-3人(指导老师不…...
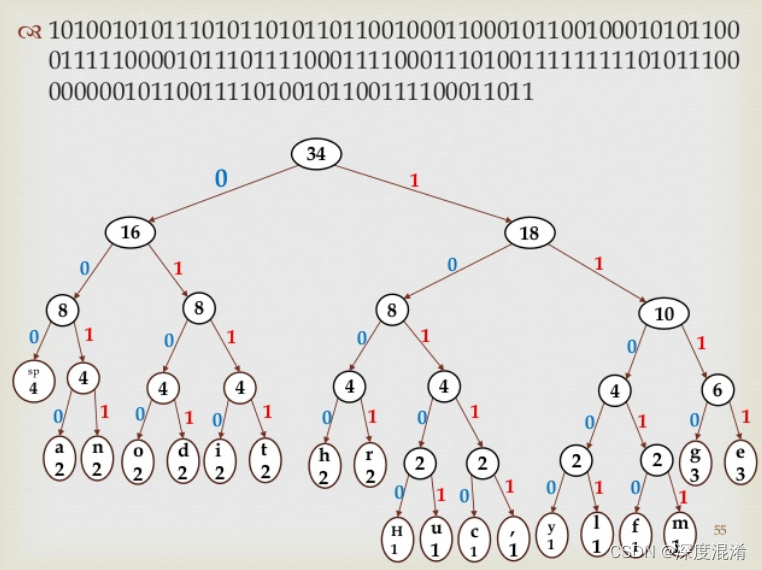
C#,哈夫曼编码(Huffman Code)压缩(Compress )与解压缩(Decompress)算法与源代码
David A. Huffman 1 哈夫曼编码简史(Huffman code) 1951年,哈夫曼和他在MIT信息论的同学需要选择是完成学期报告还是期末考试。导师Robert M. Fano给他们的学期报告的题目是,寻找最有效的二进制编码。由于无法证明哪个已有编码是…...
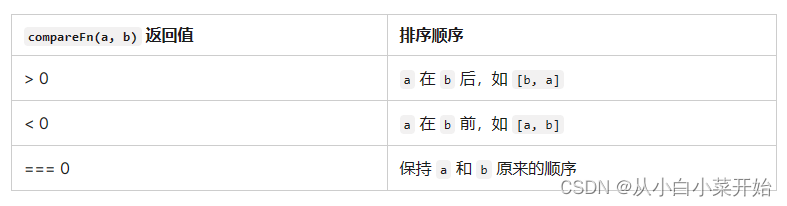
JS 对象数组排序方法测试
输出 一.Array.prototype.sort() 1.默认排序 sort() sort() 方法就地对数组的元素进行排序,并返回对相同数组的引用。默认排序是将元素转换为字符串,然后按照它们的 UTF-16 码元值升序排序。 由于它取决于具体实现,因此无法保证排序的时…...

【计算机考研】408学到什么程度才能考130?
408考130要比考研数学考130难的多 我想大部分考过408的考生都是这么认为的。408的难点在于他涉及的范围太广了,首先如果你要备考408,你要准备四门课程,分别是数据结构,计算机组成原理,操作系统和计算机网络。 这四门…...

“智农”-农业物联网可视化
大棚可视化|设施农业可视化|农业元宇宙|农业数字孪生|大棚物联网|大棚数字孪生|农业一体化管控平台|智慧农业可视化|智农|农业物联网可视化|农业物联网数字孪生|智慧农业|大棚三维可视化|智慧大棚可视化|智慧大棚|农业智慧园区|数字农业|数字大棚|农业大脑|智慧牧业数字孪生|智…...

day03-网络编程
1>TCP机械臂测试 #include<myhead.h> #define SER_IP "10.211.55.11" #define SER_PORT 8888 #define CLI_IP "10.211.55.9" #define CLI_PORT 6666 //客户端 int main(int argc, const char *argv[]) {//1、创建用于通信的套接字文件描述符int …...

Java反射,动态代理。笔记
1.pathClass Loader 和 Dex ClassLoader 在Android 5.0以下的版本中,两者之间的区别为: DexClassLoader:可加载jar、apk和dex」可以从SD卡中加载PathClassLoader:只能加载已安裝到系統中(即/data/app目录下)的apk文件但是随着Android版本的升级,到Android …...

作为团队开发组长你需要做的:
当你需要开始团队开发时,以下是一些你可能需要知道和使用的工具、实践和原则: 1. 版本控制系统 (VCS): 使用版本控制系统(如Git)来管理代码。这能确保团队成员协同工作时能够跟踪和管理代码的变更。创建分支进行开发,…...
)
Windows安装Neo4j数据库教程(3.X版本)
安装java的jdk(jdk1.8仅支持Neo4j 3.X版本)去 Index of /doc/neo4j/ 下载目标版本的Windows zip安装包将安装包解压到任意目录,并记住解压后带版本号的文件夹路径添加系统环境变量,变量名:NEO4J_HOME,变量值…...

无人机飞行控制系统技术,四旋翼无人机控制系统建模技术详解
物理建模是四旋翼无人机控制系统建模的基础,主要涉及到无人机的物理特性和运动学特性。物理建模的目的是将无人机的运动与输入信号(如控制电压)之间的关系进行数学描述。 四旋翼无人直升机是具有四个输入力和六个坐标输出的欠驱动动力学旋翼…...

程序员的金三银四求职宝典:如何在关键时期脱颖而出?
个人主页:17_Kevin-CSDN博客 随着春天的脚步渐近,程序员们的求职热潮也随之而来。在这个被称为“金三银四”的招聘季,如何从众多求职者中脱颖而出,成为了许多程序员关注的焦点。本文将为你提供一份全面的求职宝典,助你…...

分享经典、现代和前沿软件工程课程
随着信息技术的发展,软件已经深入到人类社会生产和生活的各个方面。软件工程是将工程化的方法运用到软件的开发、运行和维护之中,以达到提高软件质量,降低开发成本的目的。软件工程已经成为当今最活跃、最热门的学科之一。 本次软件工程MOOC课…...
网络工程师笔记3
IP地址类型 A类 255.0.0.0B类 255.255.0.0C类 255.255.255.0D类 E类 子网掩码:从左到右连续的确定网络位 2-4-8-16-32-64-128-256 128 : 1000 0000 64 : 0100 0000 32 : 0010 0000 16 : 0001 0000 8 &am…...

【菜鸟入门!】Matlab零基础快速入门教程
数学建模竞赛中,编程软件是必不可缺少的,比如大家都熟知的MATLAB多数同学们都会经常用到,今天给大家介绍一些MATLAB的基本元素,希望帮助大家更好的掌握编写基本的函数! 变量和数组 MATLAB 程序的基本数据单元是数组。一…...
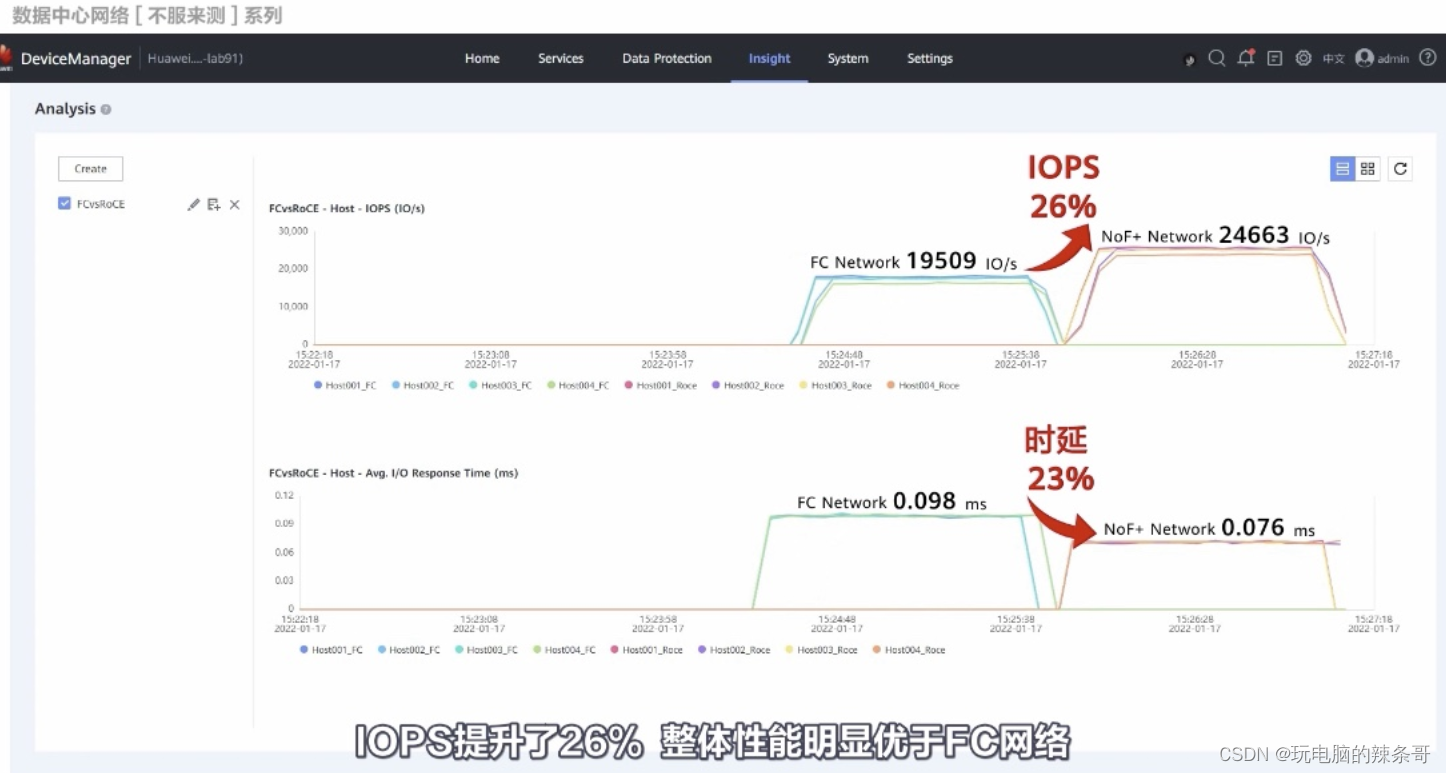
数据中心GPU集群高性能组网技术分析
数据中心GPU集群组网技术是指将多个GPU设备连接在一起,形成一个高性能计算的集群系统。通过集群组网技术,可以实现多个GPU设备之间的协同计算,提供更大规模的计算能力,适用于需要大规模并行计算的应用场景。 常用的组网技术&…...

go垃圾回收
1 go 垃圾回收变更 Go 语言的垃圾回收器(GC)自其诞生以来一直在不断演进和优化,以提高性能、减少暂停时间和对程序执行的影响。以下是一些关键的改进和变更点: 并发标记周期: Go 语言从一开始就采用了并发标记…...

如何做代币分析:以 LEO 币为例
作者: lesleyfootprint.network 编译:cicifootprint.network 数据源:LEO 代币仪表板 (仅包括以太坊数据) 在加密货币和数字资产领域,代币分析起着至关重要的作用。代币分析指的是深入研究与代币相关的数…...

数制和码制
目录 几种常见的数制 数制 基数 位权 常见的四种数制 十进制数 二进制数 八进制数 十六进制数 不同进制数的相互转换 例如 例如 编码 二-十进制码 例如 格雷码 例如 原码、反码和补码 几种常见的数制 关键术语 数制:以一组固定的符号和统一的规则来表示数值…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...
