ElasticSearch之文档的存储
写在前面
本文看下文档的存储相关内容。
1:如何确定文档存储在哪个分片?
我们需要确保文档均匀分布在所有的分片中,避免某些部分机器空闲,部分机器繁忙的情况出现,想要实现均匀分布我们可以考虑如下的几种分片路由算法:
1:round robin 轮询优点:简单缺点:数据更新、查询,删除的效率低,因为无法直接确定数据存储的分片,需要轮询,时间复杂度为O(n) 。
2:维护一个文档和分片的对应关系优点:简单缺点:需要额外维护对应关系,增加存储的成本
3:动态哈希,实时计算优点:简单,快速缺点:需要依赖于分片来计算,所以,分片数不能动态变更,除非reindex
以上三种方案,es采用的第三种,动态哈希,因为缺点相对来说,影响不是特别大,因为分片数我们完全可以事先确定好一个值,就算是确实需要修改分片数,也只需要在某次升级期间来完成即可,而前两种方案都会降低每次查询的速度,所以不可取。
动态哈希算法公式为hash(_routing)%number_of_primary_shards,这里的_routing默认是文档id,也可以通过如下方式来指定:
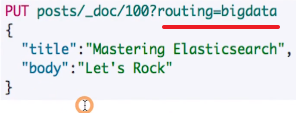
1:通过指定的方式,我们可以实现某些场景下某些数据放在同一个分片的需求。
2:es中修改分片数需要reindex的根本原因就在于,计算哈希依赖于分片数,如果分片数改变,路由分片的结果将会改变,如果不reindex将会导致大量文档无法查询。
具体如下:

2:更新和删除文档的流程
- 更新文档的流程
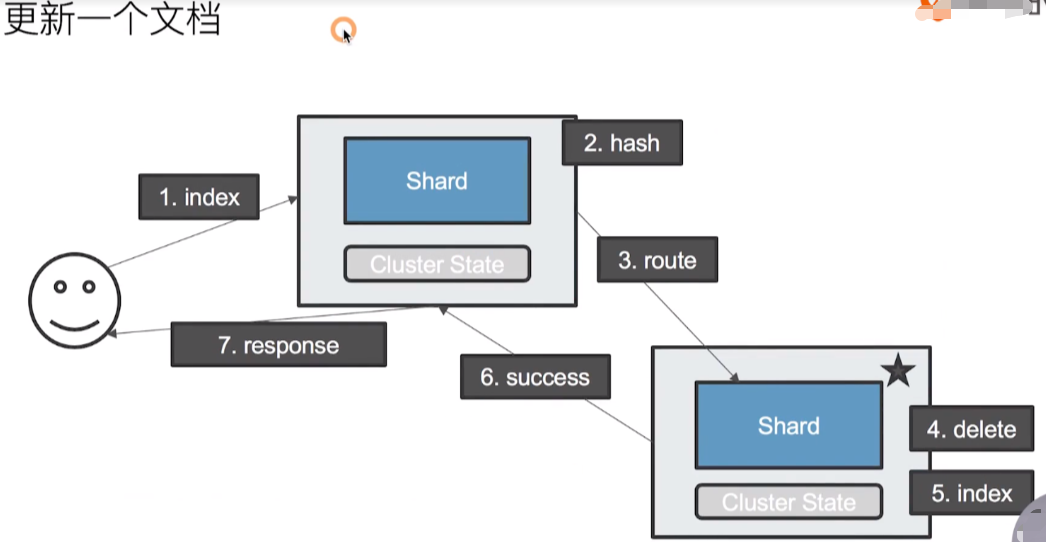
- 删除文档的流程
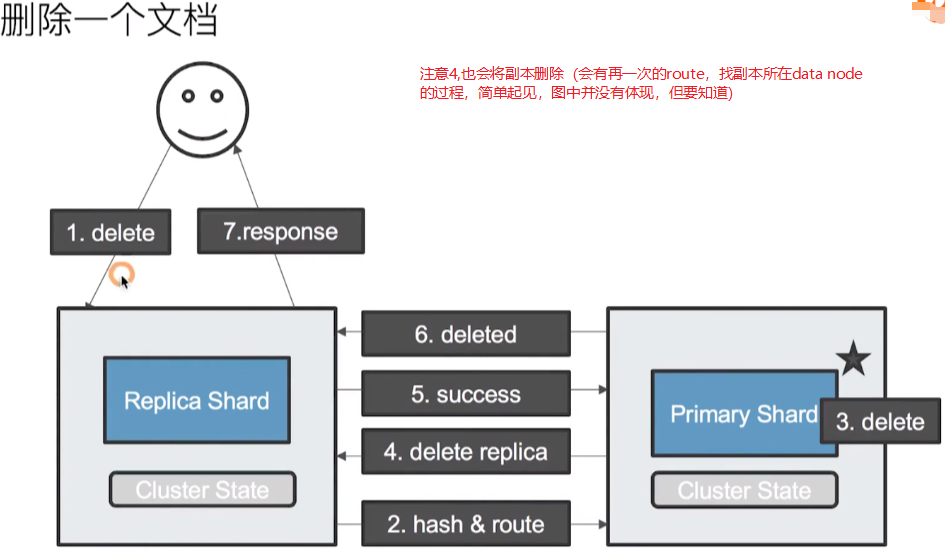
写在后面
参考文章列表
相关文章:

ElasticSearch之文档的存储
写在前面 本文看下文档的存储相关内容。 1:如何确定文档存储在哪个分片? 我们需要确保文档均匀分布在所有的分片中,避免某些部分机器空闲,部分机器繁忙的情况出现,想要实现均匀分布我们可以考虑如下的几种分片路由算…...

在Redhat 7 Linux上安装llama.cpp [ 错误stdatomic.h: No such file or directory]
前期准备 在github上下载llama.cpp或克隆。 GitHub - ggerganov/llama.cpp: LLM inference in C/C git clone https://github.com/ggerganov/llama.cpp.gitcd llama.cpp 执行make命令编译llama.cpp make 在huggingface里下载量化了的 gguf格式的llama2模型。 https:/…...

linux 常用 命令行HTTP客户端
在Linux环境中,命令行HTTP客户端是一种用于发送HTTP请求的工具,它们通常用于测试网站、服务器或API的响应。这些客户端支持各种HTTP方法,如GET、POST、PUT、DELETE等,并允许用户设置请求头、发送数据等。以下是一些常用的命令行HT…...

深入理解@Param注解:用于参数映射的利器
摘要:Param注解在Java开发中被广泛应用,它可以优雅地解决方法参数与SQL语句中占位符的映射问题,提高代码的可读性和可维护性。本文将深入探讨Param注解的背景、使用方法、解决的问题、映射原理,并对使用与不使用Param注解的情况进…...

OCP Secure boot必要特性
三点必需要求: The platform components must: 1. Provide a mechanism for securely anchoring a root of trust public key. // 提供一种用于安全地锚定信任根公钥的机制。 2. Verify the device firmware digital signature using the anchored public key /…...
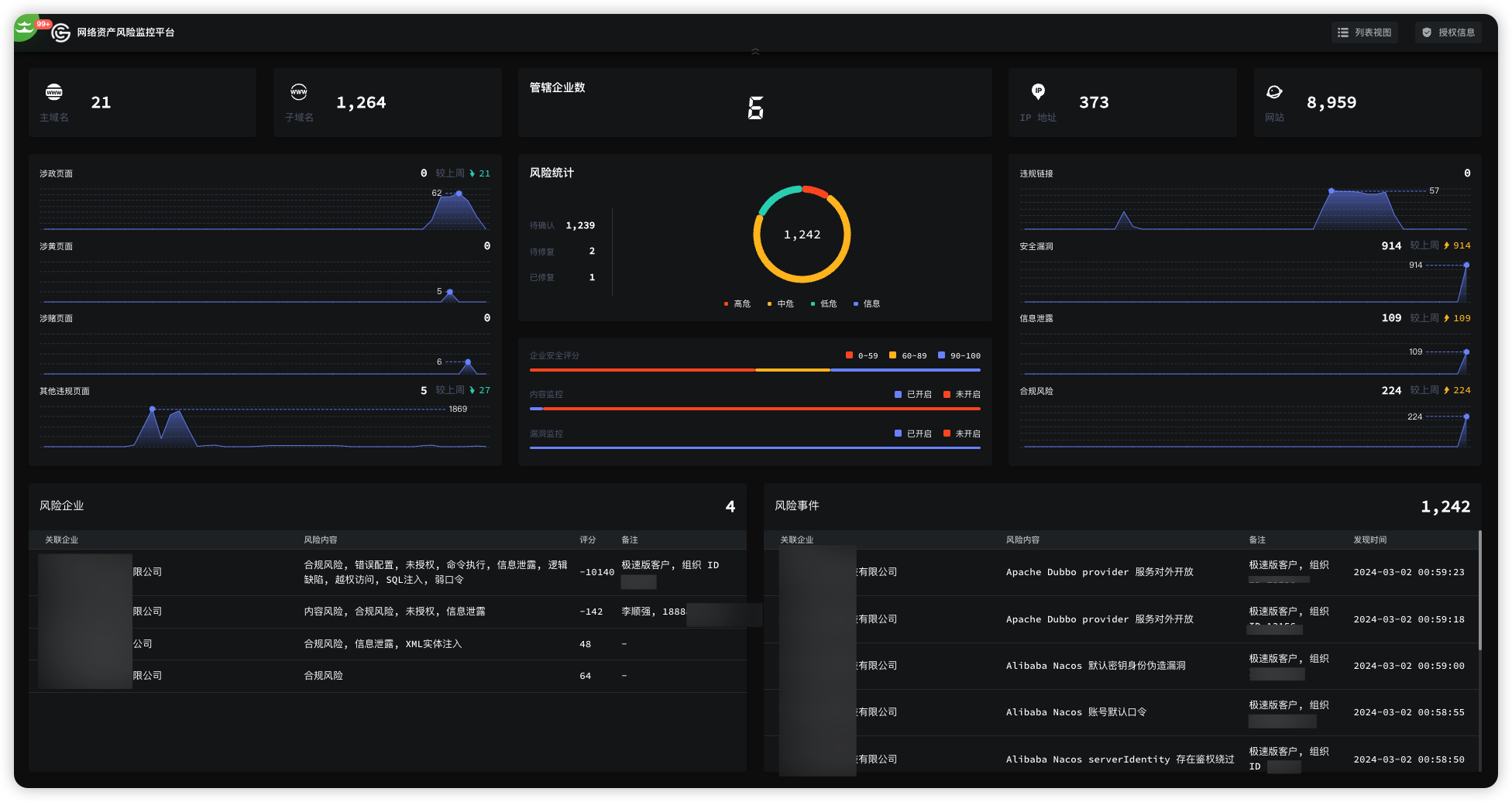
全新攻击面管理平台
首页大屏 内测阶段,免费试用一个月 有兴趣体验的师傅,来长亭云图极速版群里找我 py...

在VMware中安装CentOS 7并配置Docker
VMware安装CentOS 7 一、介绍 该文章介绍如何使用启动U盘在虚拟机里面安装系统,虚拟机版本为VMware Workstation 16 pro,Linux版本为CentOS Linux release 7.9.2009 (Core)。 二、安装 1、创建虚拟机 点击创建新的虚拟机 选择典型就可以了…...
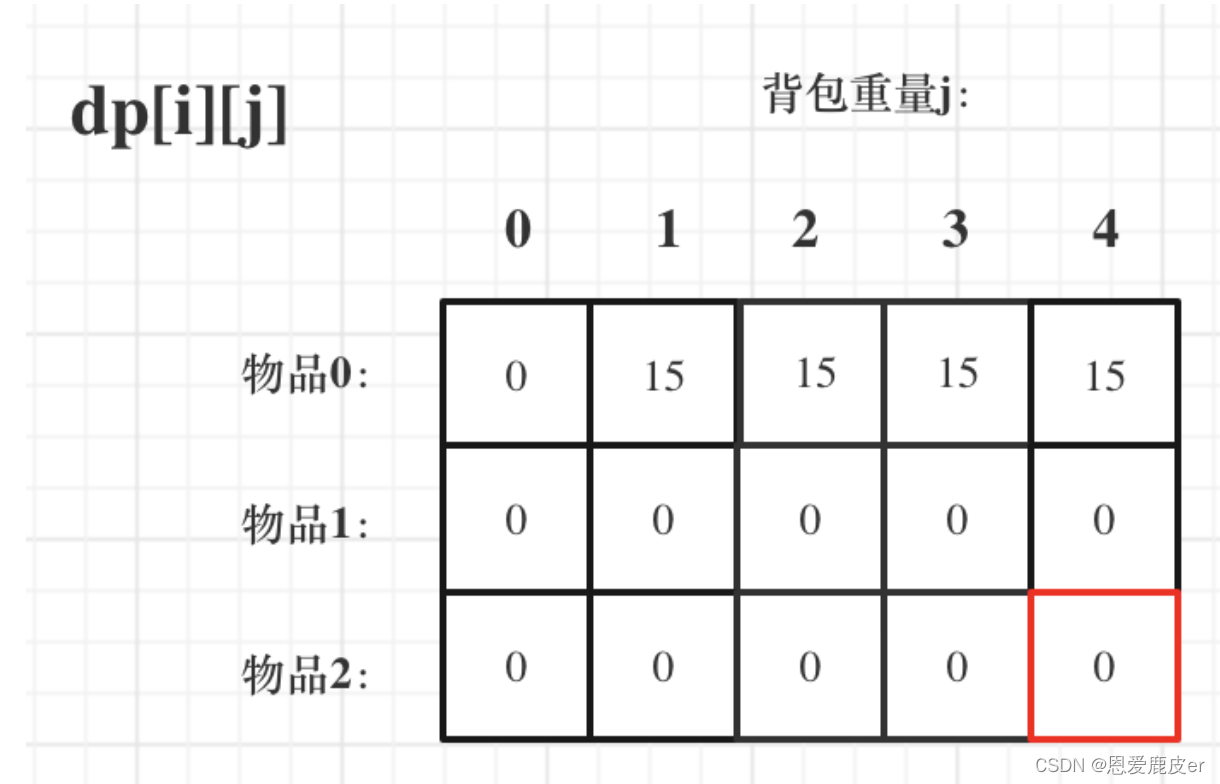
Leetcoder Day37| 动态规划part04 背包问题
01背包理论基础 面试掌握01背包,完全背包和重背包就够用了。 背包问题的理论基础重中之重是01背包,一定要理解透! 01 背包 有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品…...
)
突破编程_C++_面试(STL 编程 vector )
面试题 1 :std::vector 的底层存储机制是什么? std::vector 的底层存储机制是一个动态数组,它内部通过一片连续的内存空间来存储元素。当这个连续的内存空间不足以容纳新元素时,std::vector 会自动申请一块更大的内存空间&#x…...
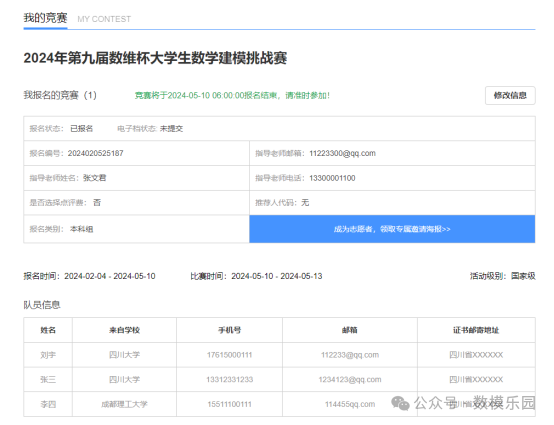
【报名指南】2024年第九届数维杯数学建模挑战赛报名全流程图解
1.官方报名链接: 2024年第九届数维杯大学生数学建模挑战赛http://www.nmmcm.org.cn/match_detail/32 2.报名流程(电脑与手机报名操作流程一致) 参赛对象为在校专科生、本科生、研究生,每组参赛人数为1-3人(指导老师不…...
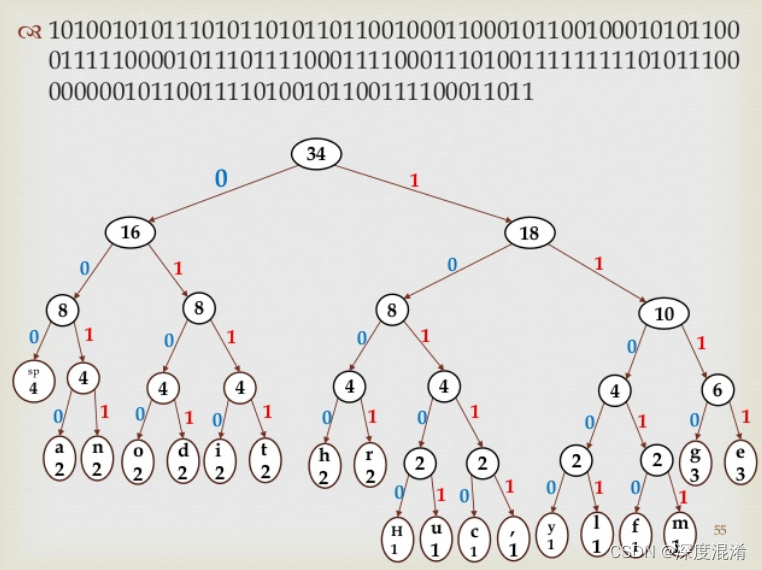
C#,哈夫曼编码(Huffman Code)压缩(Compress )与解压缩(Decompress)算法与源代码
David A. Huffman 1 哈夫曼编码简史(Huffman code) 1951年,哈夫曼和他在MIT信息论的同学需要选择是完成学期报告还是期末考试。导师Robert M. Fano给他们的学期报告的题目是,寻找最有效的二进制编码。由于无法证明哪个已有编码是…...
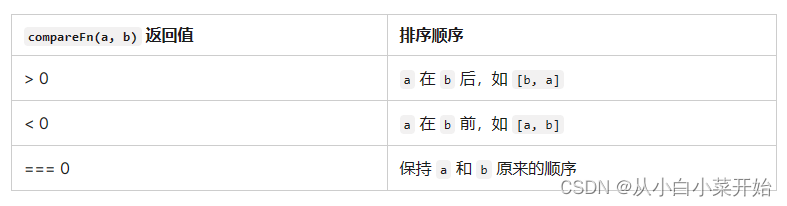
JS 对象数组排序方法测试
输出 一.Array.prototype.sort() 1.默认排序 sort() sort() 方法就地对数组的元素进行排序,并返回对相同数组的引用。默认排序是将元素转换为字符串,然后按照它们的 UTF-16 码元值升序排序。 由于它取决于具体实现,因此无法保证排序的时…...

【计算机考研】408学到什么程度才能考130?
408考130要比考研数学考130难的多 我想大部分考过408的考生都是这么认为的。408的难点在于他涉及的范围太广了,首先如果你要备考408,你要准备四门课程,分别是数据结构,计算机组成原理,操作系统和计算机网络。 这四门…...

“智农”-农业物联网可视化
大棚可视化|设施农业可视化|农业元宇宙|农业数字孪生|大棚物联网|大棚数字孪生|农业一体化管控平台|智慧农业可视化|智农|农业物联网可视化|农业物联网数字孪生|智慧农业|大棚三维可视化|智慧大棚可视化|智慧大棚|农业智慧园区|数字农业|数字大棚|农业大脑|智慧牧业数字孪生|智…...

day03-网络编程
1>TCP机械臂测试 #include<myhead.h> #define SER_IP "10.211.55.11" #define SER_PORT 8888 #define CLI_IP "10.211.55.9" #define CLI_PORT 6666 //客户端 int main(int argc, const char *argv[]) {//1、创建用于通信的套接字文件描述符int …...

Java反射,动态代理。笔记
1.pathClass Loader 和 Dex ClassLoader 在Android 5.0以下的版本中,两者之间的区别为: DexClassLoader:可加载jar、apk和dex」可以从SD卡中加载PathClassLoader:只能加载已安裝到系統中(即/data/app目录下)的apk文件但是随着Android版本的升级,到Android …...

作为团队开发组长你需要做的:
当你需要开始团队开发时,以下是一些你可能需要知道和使用的工具、实践和原则: 1. 版本控制系统 (VCS): 使用版本控制系统(如Git)来管理代码。这能确保团队成员协同工作时能够跟踪和管理代码的变更。创建分支进行开发,…...
)
Windows安装Neo4j数据库教程(3.X版本)
安装java的jdk(jdk1.8仅支持Neo4j 3.X版本)去 Index of /doc/neo4j/ 下载目标版本的Windows zip安装包将安装包解压到任意目录,并记住解压后带版本号的文件夹路径添加系统环境变量,变量名:NEO4J_HOME,变量值…...

无人机飞行控制系统技术,四旋翼无人机控制系统建模技术详解
物理建模是四旋翼无人机控制系统建模的基础,主要涉及到无人机的物理特性和运动学特性。物理建模的目的是将无人机的运动与输入信号(如控制电压)之间的关系进行数学描述。 四旋翼无人直升机是具有四个输入力和六个坐标输出的欠驱动动力学旋翼…...

程序员的金三银四求职宝典:如何在关键时期脱颖而出?
个人主页:17_Kevin-CSDN博客 随着春天的脚步渐近,程序员们的求职热潮也随之而来。在这个被称为“金三银四”的招聘季,如何从众多求职者中脱颖而出,成为了许多程序员关注的焦点。本文将为你提供一份全面的求职宝典,助你…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...
