叠罗汉游戏
题目描述
农场的N头奶牛喜欢玩叠罗汉游戏,就是几头奶牛1头奶牛接着1头奶牛的站成一柱子形状。不过奶牛的力量不一样,用数值Ci表示第i头奶牛它的上面最多可以站多少头奶牛,问这些奶牛最少可以站成几个柱子形状。
输入格式
输入文件名:638.in
第一行1个整数N,表示有多少头奶牛。1<=N<=1000。
第二行N个正整数Ci,表示这些奶牛的力量。0<=Ci<=1000。
输出格式
输出文件名:638.out
一个整数,表示最少成几个“罗汉”。
输入/输出例子1
输入:
5
0 2 1 2 2
输出:
2
样例解释
可以第1、第3、第2头奶牛从上向下叠罗汉;
第4、第5头奶牛叠罗汉。
My answer:
#include<bits/stdc++.h>
using namespace std;
int cmp(int x,int y)
{return x>y;
}
int a[1005],n,s,sum;
int main()
{cin>>n;for(int i=1;i<=n;i++) {cin>>a[i];a[i]++;}sort(a+1,a+n+1,cmp);while(s<=n) s+=a[sum++];cout<<sum-1;return 0;
}相关文章:

叠罗汉游戏
题目描述 农场的N头奶牛喜欢玩叠罗汉游戏,就是几头奶牛1头奶牛接着1头奶牛的站成一柱子形状。不过奶牛的力量不一样,用数值Ci表示第i头奶牛它的上面最多可以站多少头奶牛,问这些奶牛最少可以站成几个柱子形状。 输入格式 输入文件名&#…...

太阳能风吸式杀虫灯是什么
TH-FD1随着农业科技的不断进步,太阳能风吸式杀虫灯作为一种新兴的绿色农业技术,正逐渐走进人们的视野。这种集太阳能和风吸技术于一体的杀虫设备,不仅具有环保节能的特点,还能有效减少农药使用,提高农产品质量…...
SpringBoot启动扩展应用:干预优化+加快启动时间
一、SpringBoot启动配置原理简述 本内容直接查看分析SpringBoot启动配置原理,传送门: 二、SpringBoot启动过程干预 Spring Boot启动过程中我们可以实现以下干预工作: 修改Spring Boot默认的配置属性。使用ConfigurationProperties和Enable…...
探索Linux世界:初次接触和基本指令(文件操作)
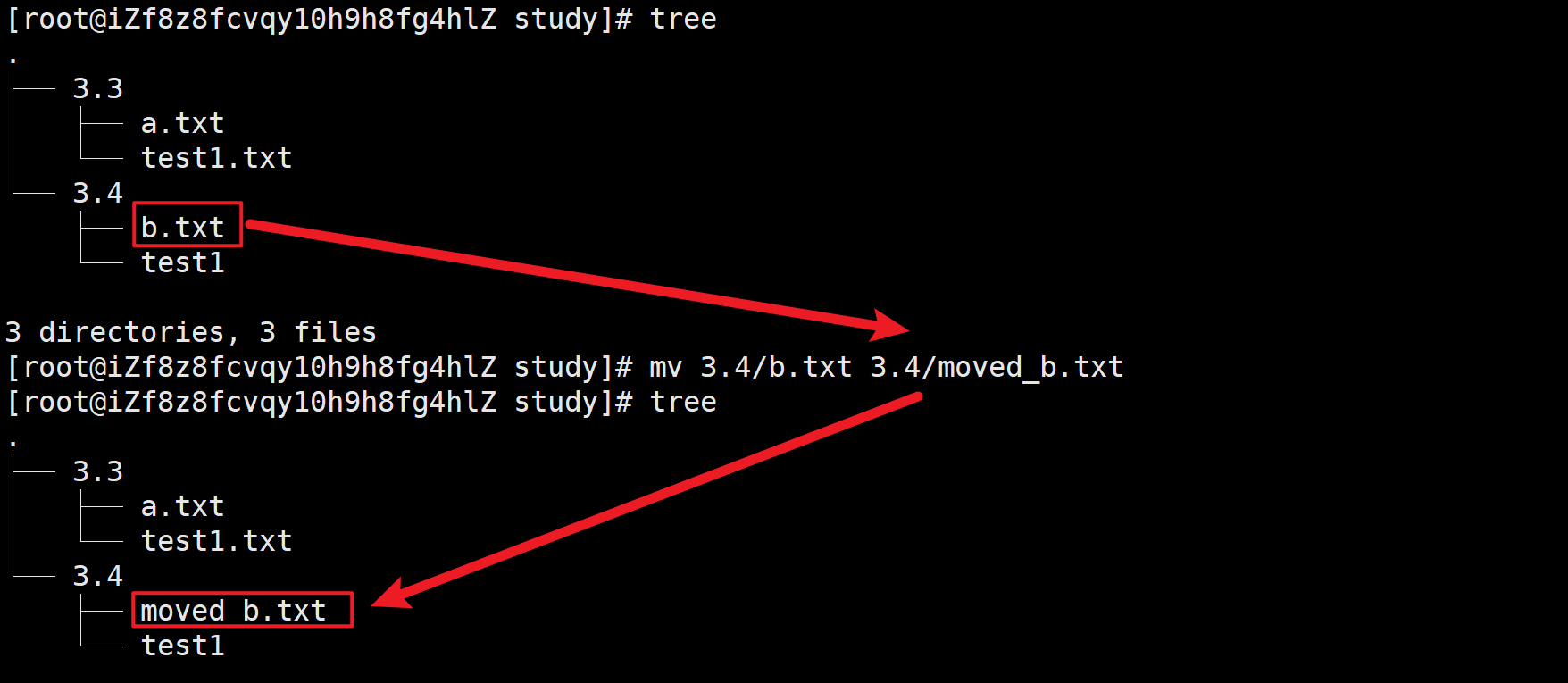
文章目录 1.基本介绍和准备2.基本指令和Linux的基本操作3.几个重要基本指令3.1 ls - 列出文件和目录3.1.1文件的知识3.1.2 .和..文件 3.2pwd - 显示当前工作目录3.2.1路径知识 3.3 cd - 切换目录3.4 touch - 创建文件或更新时间戳3.5mkdir - 创建新目录3.6rm - 删除文件或目录3…...
)
递归函数(c++题解)
题目描述 对于一个递归函数w(a, b, c)。 如果a < 0 or b < 0 or c < 0就返回值1。 如果a > 20 or b > 20 or c > 20就返回W(20,20,20)。 如果a < b并且b < c 就返回w(a, b, c − 1) w(a, b − 1, c − 1) − w(a, b − 1, c), 其它别…...

Qt将Unicode转换成UTF8中文
解析字符串,并将里面的Unicode转换成中文 QString unicodeToUtf8(QString unicode) {QString result;for (int i 0; i < unicode.length(); i){QString flag unicode.mid(i,2); if (flag "\\u"){QString s1 unicode.mid(i 2, 4);result.append(s…...
HTTP 的 multipart 类型
上一篇文章讲到 http 的 MIME 类型 http MIME 类型 里有一个 multipart 多部分对象集合类型,这个类型 http 指南里有讲到:MIME 中的 multipart(多部分)电子邮件报文中包含多个报文,它们合在一起作为单一的复杂报文发送…...
)
【NR 定位】3GPP NR Positioning 5G定位标准解读(二)
目录 前言 2. UE定位方法的作用 3. 标准UE定位方法 3.1 引言 3.2 网络辅助的GNSS方法 3.3 OTDOA定位 3.4 增强小区ID方法 3.5 气压传感器定位 3.6 WLAN定位 3.7 蓝牙定位 3.8 TBS定位 3.9 运动传感器定位 3.10 NR增强小区ID方法 3.11 多RTT定位 3.12 DL-AoD定位…...

为何代理IP的稳定性不如有线IP?
代理IP与网线IP的稳定性之间存在差异的原因在于它们的工作机制和服务环境的不同。以下是代理IP不如网线IP稳定的一些主要原因: 1. 服务提供商的质量: - 动态分配:代理IP通常是动态分配的,这意味着每次请求或每隔一段时间ÿ…...

【c++】 string类的模拟实现
1.浅拷贝 浅拷贝:也称位拷贝,编译器只是将对象中的值拷贝过来。如果对象中管理资源,最后就会导致多个对象共享同一份资源,当一个对象销毁时就会将该资源释放掉,而此时另一些对象不知道该资源已经被释放,以…...

transformer--transformer模型构建和测试
前面几节进行了各种组件的学习和编码,本节将组件组成transformer,并对其进行测试 EncoderDecoder 编码器解码器构建 使用EnconderDecoder实现编码器-解码器结构 # 使用EncoderDeconder类实现编码器和解码器class EncoderDecoder(nn.Module):def __ini…...

从0到1全流程使用 segment-anything
从0到1全流程使用 segment-anything 一、安装 anaconda 一、下载 anaconda 二、以管理员身份运行安装 1、勾选 Just Me 2、统一安装路径(后续 python 等包也安装至此目录) 3、勾选 add to path 然后安装即可。 三、修改 Anaconda 默认路径及默认缓存路径 Anaconda 默认下…...
Window系统部署Splunk Enterprise并结合内网穿透实现远程访问本地服务
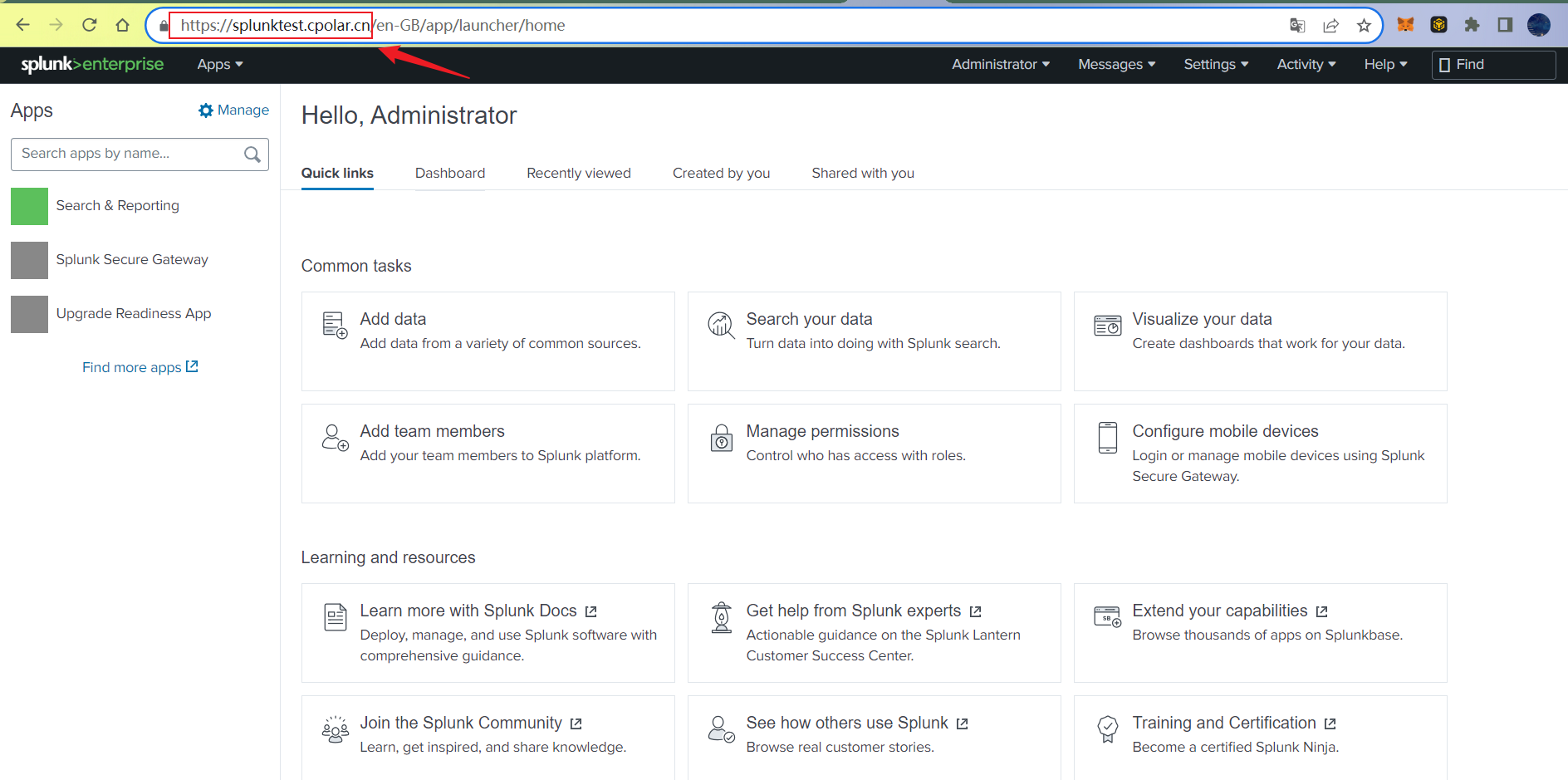
文章目录 前言1. 搭建Splunk Enterprise2. windows 安装 cpolar3. 创建Splunk Enterprise公网访问地址4. 远程访问Splunk Enterprise服务5. 固定远程地址 前言 本文主要介绍如何简单几步,结合cpolar内网穿透工具实现随时随地在任意浏览器,远程访问在本地…...
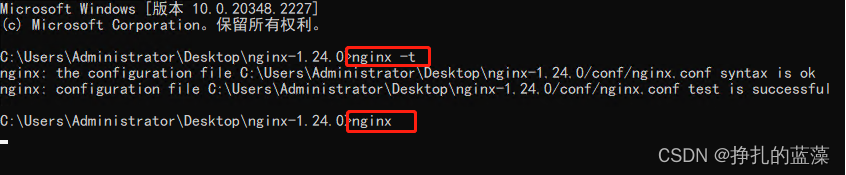
Windows服务器:通过nginx反向代理配置HTTPS、安装SSL证书
先看下效果: 原来的是 http,配置好后 https 也能用了,并且显示为安全链接。 首先需要 SSL证书 。 SSL 证书是跟域名绑定的,还有有效期。 windows 下双击可以查看相关信息。 下载的证书是分 Apache、IIS、Tomcat 和 Nginx 的。 我…...

LeetCode67 二进制求和
题目 给你两个二进制字符串 a 和 b ,以二进制字符串的形式返回它们的和。 示例 示例 1:输入:a "11", b "1" 输出:"100" 示例 2:输入:a "1010", b "1011" 输出&…...

python | 列表,元组,字符串,集合,字典
列表: 可以容纳任意数目不同类型的元素(支持我们学过的任意数据类型)元素之间有先后顺序用中括号包裹,每个元素用逗号隔开 例如: students [林黛玉,薛宝钗,贾元春,贾探春,史湘云,妙玉,贾迎春,贾惜春,王熙凤,贾巧姐…...

稀疏图带负边的全源最短路Johnson算法
BellmanFord算法 Johnson算法解决的问题 带负权的稀疏图的全源最短路 算法流程 重新设置的每条边的权重都大于或等于0,跑完Djikstra后得到的全源最短路,记得要还原,即:f(u,v) d(u,v) - h[u] h[v] 例题...

oracle基础体系
一、 Oracle数据库服务器 数据库在各个行业都会有使用到;其实,我们平时无论是在与客户沟通或者交流中,所说的Oracle数据库是指Oracle数据库服务器(Oracle Server),它由Oracle实例(Oracle Instan…...

k8s运维问题整理
1.宕机或异常重启导致etcd启动失败 服务器非正常关机(意外掉电、强制拔电)后 etcd 数据损坏。 查看apiserver日志发现出现报错Error while dialing dial tcp 127.0.0.1:2379: connect: connection refused,2379是etcd的端口,那么a…...
设计模式分类和六大设计原则)
设计模式(一)设计模式分类和六大设计原则
0.设计模式的分类 GoF提出的设计模式总共有23种,根据目的准则分类分为三大类: 创建型模式,共五种:单例模式、工厂方法模式、抽象工厂模式、建造者模式、原型模式。 结构型模式,共七种:适配器模式、装饰模式…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...
