力扣hot100:42.接雨水
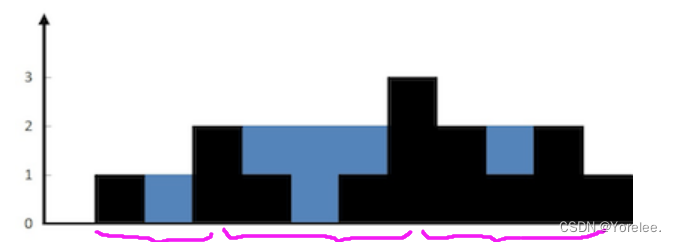
什么时候能用双指针?
(1)对撞指针:
①两数和问题中可以使用双指针,先将两数和升序排序,可以发现规律,如果当前两数和大于target,则右指针向左走。
②接雨水问题中,左边最大 和 右边最大 可以通过双指针 + 双变量维护。
(2)快慢指针:
①比如找到链表的中点,快指针一次走两步,满指针一次走一步。
(3)滑动窗口:
滑动窗口维护当前窗口内满足要求。而双指针可以在整个数组中考虑问题。
动态变化窗口大小:
①比如接雨水这里,考虑极限:满足右边界大于等于左边界,此时左边界移动。
固定窗口大小:
①找到字符串中所有字母异位词:固定窗口大小为目标串,移动记录窗口时,增加窗口末尾字符对应的个数,减少滑出窗口的字符对应的个数。

一、从单个水柱本身考虑
下标为i的水柱能接的雨水,取决于它左边最高的水柱 和 右边最高的水柱的最小值(包括它本身)。
为了理解这一性质,我们可以这样想象:取出左边最高和最边最高的水柱,将其比作一个碗的边界。中间坑坑洼洼,忽高忽低,高低错落,碗面中的一个点的能接水的最高高度是多少呢? 就是碗边界的最小值-该点的高度。
因此,从单个水柱考虑,我们只需要能够求出这个问题即可。
一、动态规划
我们定义两个数组:
left_max[i]:表示从0~i 中 水柱高度的最大值
right_max[i]: 表示从i~height.size()-1中水柱高度的最大值
class Solution {
public:int trap(vector<int>& height) {int n=height.size();vector<int> left_max(n);vector<int> right_max(n);left_max[0]=height[0];right_max[n-1]=height[n-1];//求出左边最大值for(int i=1;i<n;++i){left_max[i]=max(left_max[i-1],height[i]);}//求出右边最大值for(int i=n-2;i>=0;--i){right_max[i]=max(right_max[i+1],height[i]);}long long ans=0;for(int i=0;i<n;++i){ans+=min(left_max[i],right_max[i])-height[i];}return ans;}
};二、双指针
class Solution {
public:int trap(vector<int>& height) {int n=height.size();int left_max=height[0];int right_max=height[n-1];int left=0;int right=n-1;long long ans=0;while(left<right){left_max=max(left_max,height[left]);right_max=max(right_max,height[right]);if(left_max>right_max){//说明右边这个right柱子 取决于 其右边的最高高度。ans+=right_max-height[right];--right;}else{ans+=left_max-height[left];++left;}}return ans;}
};二、从整体水柱考虑
从左向右依次看,对于第一个水柱而言,直到遇到一个比它高的水柱,其中间的水柱都由第一个水柱的高度决定。一种特殊情况是,最后一个找不到比它高的水柱,此时对它我们从右往左看即可。(左右对称)
class Solution {
public:int trap(vector<int>& height) {int left=0;//左边指向当前左柱子,当左柱子低于右柱子时,它已经不再能装水了 int right=1;//右边往右一直寻找比左柱子高的 或 相等高度的柱子int sum=0;while(right<height.size()){if(height[right]>=height[left]){int temp=height[left];while(left!=right){sum+=temp-height[left];++left;}}++right;}if(left!=height.size()-1){int end=left;left=height.size()-1;right=left-1;while(right>=end){if(height[right]>=height[left]){int temp=height[left];while(left!=right){sum+=temp-height[left];--left;}}--right;}}return sum;}
};相关文章:
力扣hot100:42.接雨水
什么时候能用双指针? (1)对撞指针: ①两数和问题中可以使用双指针,先将两数和升序排序,可以发现规律,如果当前两数和大于target,则右指针向左走。 ②接雨水问题中,左边最…...
搜索回溯算法(DFS)1------递归
目录 简介: 递归问题解题的思路模板 例题1:汉诺塔 例题2:合并两个有序链表 例题3:反转链表 例题4:两两交换链表中的节点 例题5:Pow(x,n)-快速幂 结语: 简介&…...

workstation 用途
一 workstation 用途 强大的桌面虚拟化 允许创造多种操作系统可以不用重启就跨不同操作系统进行操作可以提供隔离的安全环境 连接到vsphere 可以远程登陆服务器管理物理主机和虚拟主机任何时间都可登陆提高虚拟机效率 为任何平台开发和测试 1)借助一台单一本地…...

【三维重建】【SLAM】SplaTAM:基于3D高斯的密集RGB-D SLAM(CVPR 2024)
题目:SplaTAM: Splat, Track & Map 3D Gaussians for Dense RGB-D SLAM 地址:spla-tam.github.io 机构:CMU(卡内基梅隆大学)、MIT(美国麻省理工) 总结:SplaTAM,一个新…...

Go Barrier栅栏
1. 简介 实现与pythonthreading.Barrier库类似的功能,多线程同时等待达到指定数量一起放行。 有待改进地方: wait方法没有支持context控制。 2. 代码 import ("context""golang.org/x/sync/semaphore""sync/atomic" …...

[蓝桥杯 2023 省 B] 冶炼金属
P9240 [蓝桥杯 2023 省 B] 冶炼金属 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 参考题解: #C3150——蓝桥杯2023年第十四届省赛真题-冶炼金属(分块)-Dotcpp编程社区 https://www.bilibili.com/video/BV1wc411x7KU/?spm_id_from333.1007.top_right_bar_windo…...

续Java的执行语句、方法--学习JavaEE的day07
day07 一、特殊的流程控制语句 break(day06) continue 1.理解: 作用于循环中,表示跳过循环体剩余的部分,进入到下一次循环 做实验: while(true){ System.out.println(“111”); System.out.println(“222”); if(true){ conti…...

公网IP怎么获取?
公网IP是网络中设备的唯一标识符,用于在Internet上进行通信和定位。对于普通用户来说,了解如何获取自己的公网IP是很有必要的,本文将介绍几种获取公网IP的方法。 方法一:通过路由器查询 大多数家庭和办公室使用的路由器都会有一个…...

连接未来:探索嵌入式系统的智能化之路
连接未来:探索嵌入式系统的智能化之路 嵌入式系统的智能化是连接未来的关键之一。以下是对这一主题的小点论述: 1. 嵌入式系统的定义和特点 嵌入式系统是一种特殊用途的计算机系统,通常嵌入在其他设备中,具有小巧、低功耗、实时…...
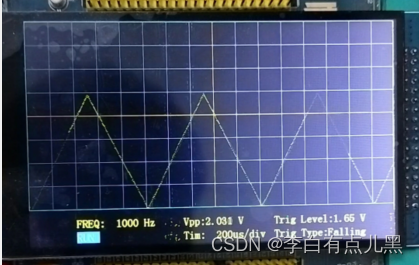
基于STM32制作的示波器(可对任意信号进行描点)
基于STM32制作的示波器(可对任意信号进行描点) 注意:用的屏幕是TFT-LCD(MCU 屏)正点原子同款屏幕 液晶显示器,即 Liquid Crystal Display,利用了液晶导电后透光性可变的特性,配合显…...

WEB APIs (5)
window对象 BOM(浏览器对象模型) 其为js操作浏览器提供了方法 window对象是一个全局变量,是BOM树根节点 BOM的属性和方法都是window的,如document、console.log()等 var定义在全局全局作用域中的变量、函数都会变成window对象…...

物联网常见协议篇
在物联网环境中,物联网协议承担着关键作用,而新手了解物联网协议如传输协议、通讯协议和行业协议等。 一、物联网协议 物联网协议是物联网环境中的关键组成部分,它承担着设备间通信和数据传输的重要任务。这些协议根据其作用的不同ÿ…...
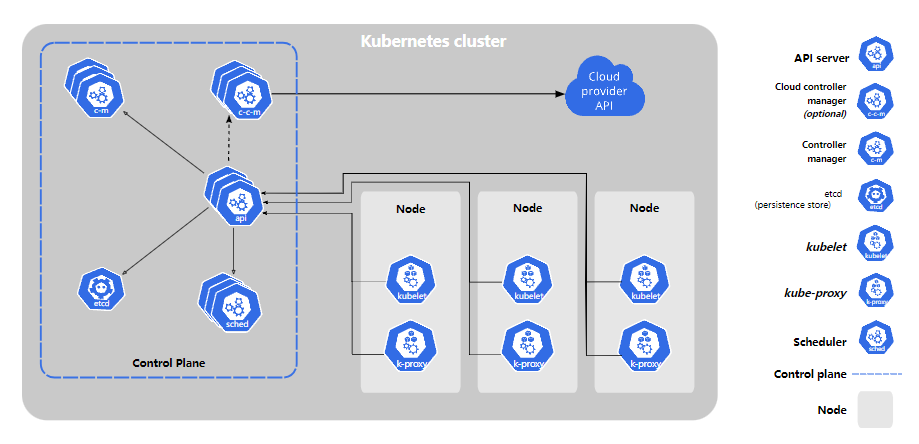
Kubernetes-1
学习Kubernetes第一天 k8s-11、什么是Kubernetes2、配置Kubernetes2.1、准备三台全新的虚拟机2.2、关闭防火墙和SElinux2.3、修改主机名2.4、升级操作系统(三台一起操作)2.5、配置主机hosts文件,相互之间通过主机名互相访问2.6、配置master和node之间的免密通道2.7、…...

SpringMVC框架②
三、RequestMapping注解 3、RequestMapping注解的value属性 必须设置 发送一个请求最直观的表示方式就是一个请求路径 altenter 进入接口方法 再用 alte7 查看里面的属性 value值可以是数组 value{"test","test1"} 只满足任何一个请求地址就会调用此方…...
springboot230基于Spring Boot在线远程考试系统的设计与实现
在线远程考试系统设计与实现 摘 要 信息数据从传统到当代,是一直在变革当中,突如其来的互联网让传统的信息管理看到了革命性的曙光,因为传统信息管理从时效性,还是安全性,还是可操作性等各个方面来讲,遇到…...
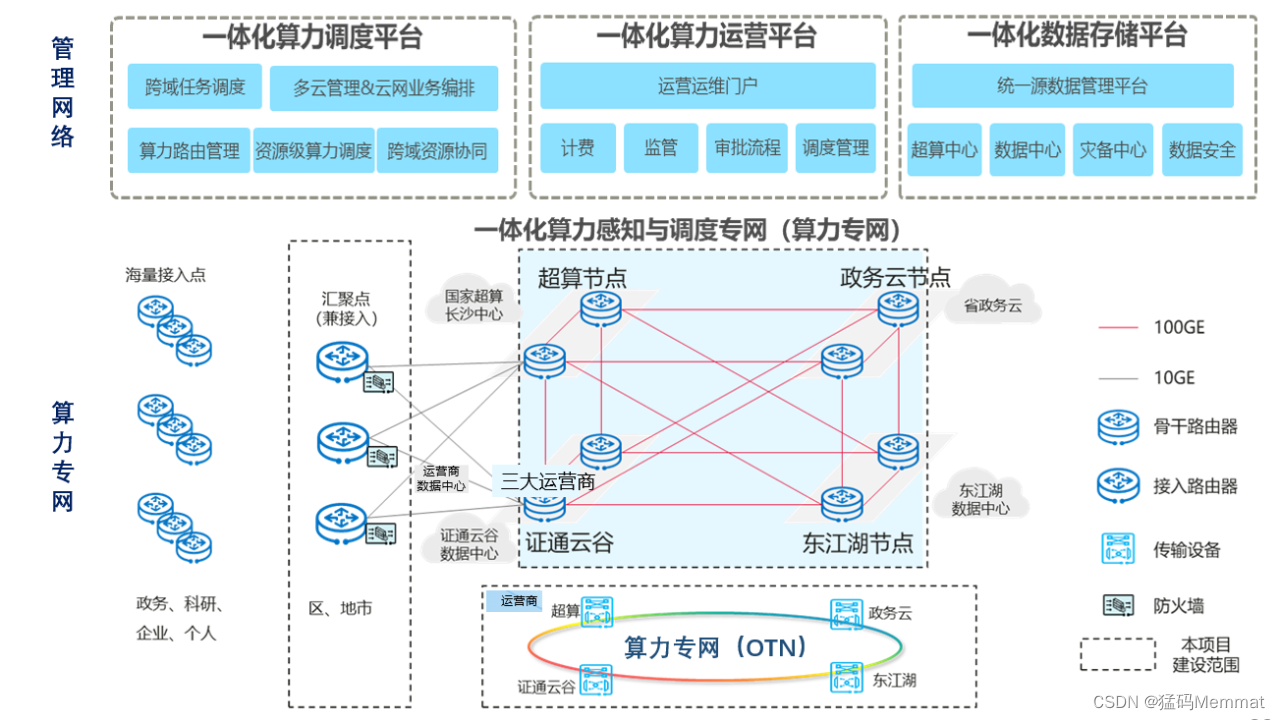
盘点:国家智能算力中心
文章目录 1. Main2. My thoughtsReference 1. Main 按照《中国算力白皮书(2022年)》的定义,算力主要分为四部分:通用算力、智能算力、超算算力、边缘算力。通用算力以CPU芯片输出的计算能力为主;智能算力以GPU、FPGA、…...

【C++】7-2 寻找完美数 分数 10
7-2 寻找完美数 分数 10 全屏浏览 切换布局 作者 李祥 单位 湖北经济学院 所有真因子之和小于其本身的数称为亏数。 如:4 的真因子 1、2 之和为 3,小于 4,是亏数。 所有真因子之和大于其本身的数称为盈数。 如:12 的真因子 1…...
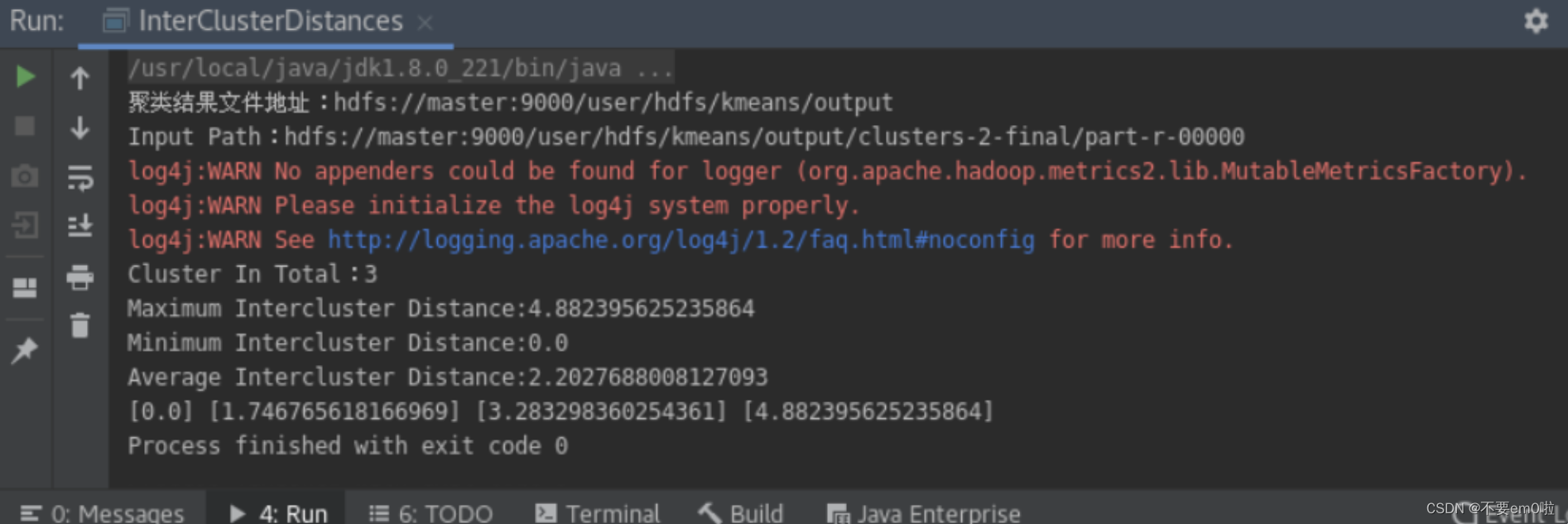
基于Mahout实现K-Means聚类
需求分析 需要对数据集进行预处理,选择合适的特征进行聚类分析,确定聚类的数量和初始中心点,调用Mahout提供的K-Means算法进行聚类计算,评估聚类结果的准确性和稳定性。同时,需要对Mahout的使用和参数调优进行深入学习…...
)
科技的成就(五十七)
535、Machine Learning "1959 年 7 月,塞缪尔首创 Machine Learning 一词。塞缪尔在“Some Studies in Machine Learning Using theGame of Checkers”一文中给 Machine Learning 下了个非正式定义:没有明确编程指令的情况下,能让计算机…...

动态IP代理技术在网络爬虫中的实际使用
目录 一、动态IP代理技术概述 二、动态IP代理技术的优势 三、动态IP代理技术的实际应用 四、注意事项 五、案例分析 六、结论 随着互联网的迅猛发展,网络爬虫成为了获取信息、分析数据的重要工具。然而,在进行大规模爬取时,爬虫常常面临…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...
