[动态规划]---part1
前言
作者:小蜗牛向前冲
专栏:小蜗牛算法之路
专栏介绍:"蜗牛之道,攀登大厂高峰,让我们携手学习算法。在这个专栏中,将涵盖动态规划、贪心算法、回溯等高阶技巧,不定期为你奉上基础数据结构的精彩算法之旅。一同努力,追逐技术的星辰大海。"
目录
一、什么是动态规划
1、什么是动态规划
2、动态规划的学习
二、动态规划刷题
1、第 N 个泰波那契数
a、解题思路:
b、代码
2、 面试题 08.01. 三步问题
a、解题思路:
b、代码
3 、746. 使用最小花费爬楼梯
a、解题思路
b、代码
4、解码方法
a、解题思路
b、代码
c、代码优化
5、不同路径(medium)
a、解题思路
b、代码
本期我们将探讨动态规划,并提供5道经典动态规划问题,难度由浅入深。
一、什么是动态规划
1、什么是动态规划
在学习算法的过程中,我们往往会遇到一些算法题是要用动态规划来解决。
但是做为小白的我们哪里知道动态规划是什么?
从概念上说
动态规划(Dynamic Programming)是一种解决复杂问题的算法设计技术。它通常用于解决具有重叠子问题和最优子结构性质的问题,通过将问题分解为更小的子问题,并利用子问题的解来构建原始问题的解。

看完概念我们知道什么是动态规划,求重叠类子问题的 一般会用到动态规划的思路。
那我们如何求学习动态规划
2、动态规划的学习
对于算法类题目,在我们掌握算法的基本原理后,就是进行大量刷题,进经验的总结。
求解动态规划的五步骤:
1、状态表示
在求解过程中,我们往往要创建dp表(其实就是数组),状态表示就是我们要找出dp表中值的含义是什么。
状态表 怎么来?
- 根据题目要求
- 经验+题目要求
- 分析题目的过程中,发现重复子问题
2、状态转移方程
简单说是和dp[i]有关的一个方程
3、初始化
保证在填写dp表的时候不越界
4、填写顺序
根据前面的计算得来,可以从前往后,也可以从后往前。
5、返回值
根据题目要求+状态表示
讲完了解题步骤,下面就进行刷题训练。
特别提醒:后面博客会带领大家由易到难进行刷题,每期都为五题。
二、动态规划刷题
1、第 N 个泰波那契数
泰波那契序列 Tn 定义如下:
T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2
给你整数
n,请返回第 n 个泰波那契数 Tn 的值。
示例 1:
输入:n = 4 输出:4 解释: T_3 = 0 + 1 + 1 = 2 T_4 = 1 + 1 + 2 = 4示例 2:
输入:n = 25 输出:1389537提示:
0 <= n <= 37- 答案保证是一个 32 位整数,即
answer <= 2^31 - 1。
a、解题思路:
1、题目中的状态表示是什么?

dp[i] 表⽰:第 i 个泰波那契数的值。
2、状态转移方程
由题目意很很容易知道是T(n) = T(n-1)+T(n-2)+T(n-3)
3、初始化dp表
为了防止数组越界我们只需要初始化:
dp[0]=0;
dp[1]=1;
dp[2]=1;
4、 填表顺序
由状态方程+题意知道从左往右填写到N
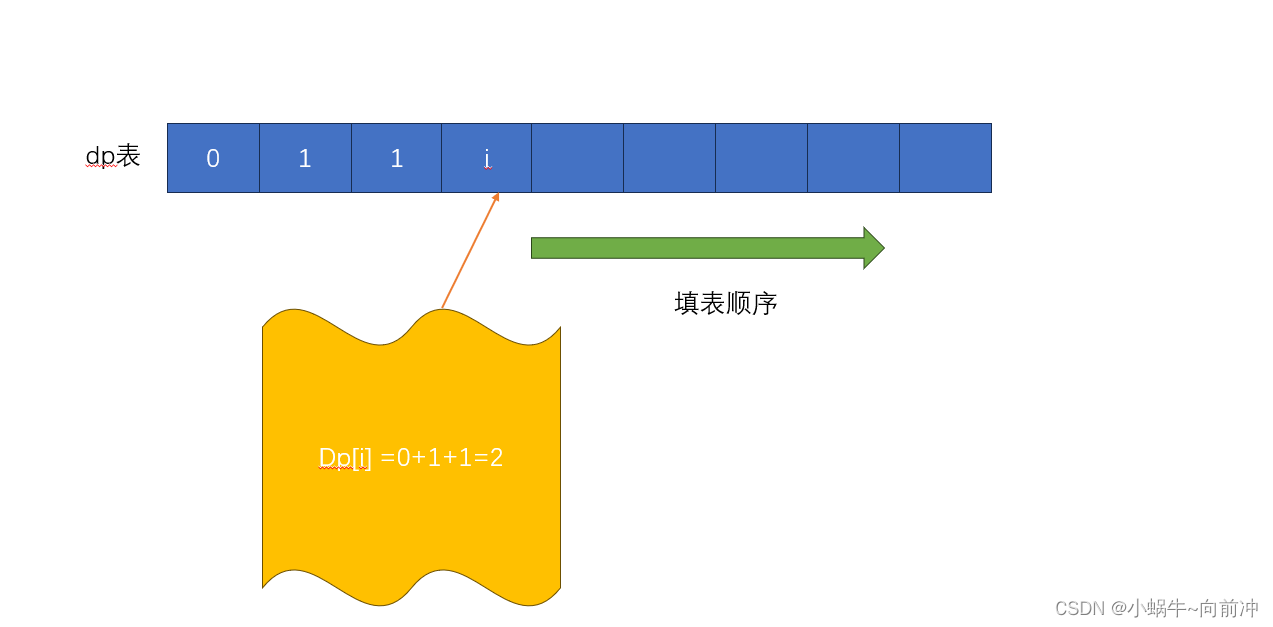
5、返回值
根据题目要求和dp[i]就为dp[n]
b、代码
class Solution {
public:int tribonacci(int n) {//动态规划//1.创建dp表//2.初始化表//3.填表//4.返回值//处理边界情况if(n==0)return 0;if(n==1||n==2)return 1;//1、创建dp表vector<int> dp(n+1);//2、初始化表dp[0]=0,dp[1]=1,dp[2]=1;//3、填表for(int i = 3;i<=n;i++){dp[i] = dp[i-1]+dp[i-2]+dp[i-3];}//4、返回return dp[n];}
};Leetcode 测试结果:
2、 面试题 08.01. 三步问题
三步问题。有个小孩正在上楼梯,楼梯有n阶台阶,小孩一次可以上1阶、2阶或3阶。实现一种方法,计算小孩有多少种上楼梯的方式。结果可能很大,你需要对结果模1000000007。
示例1:
输入:n = 3 输出:4 说明: 有四种走法示例2:
输入:n = 5 输出:13提示:
- n范围在[1, 1000000]之间
a、解题思路:
从0位置开始跳,下面我们来思考一下题意:
----->(表示跳台阶)
n=1时候
从0----->1
走法为1
n=2时候
从0----->2
或者说我们让1----->2因为从 0----->1的走法我们已经考虑过了
走法为2
n=3时候
从0----->3或者说
我们让1----->3因为从 0----->1的走法我们已经考虑过了走法为1
也可以2----->3因为从 0----->2的走法我们已经考虑过了走法为2
走法为1+1+2=4
n=4时候
不管怎么说先走到1,在从1----->4走法为1
不管怎么说先走到2,在从2----->4走法为2
不管怎么说先走到3,在从3----->4走法为4
总共走法:1+2+4=7
大家这里是不是已经思路清晰起来了
1、转态表示
以i位置为结尾,正好是到达第N个台阶,所以我们认为:
dp[i]表示:到达i位置时,一共有多少方法。

2、状态转移方程
以i位置的状态,最近进的一步进行划分
从(i-1)--->i dp[i-1]种走法
从(i-2)--->i dp[i-2]种走法
从(i-3)--->i dp[i-3]种走法
所以状态方程为:dp[i]=dp[i-1]+dp[i-2]+dp[i-3] ;
3、初始化
这里我们注意我们用不到i==0,因为0台阶的研究没有意义。
dp[1] = 1, dp[2] = 2, dp[3] = 4;
4、 填表顺序
根据前面的推断肯定是从左往右。
5、返回值
根据题目要求和dp[i]就为dp[n]
b、代码
这题虽然和第一题非常相似但是有细节要处理、
class Solution {
public://取模const int MOD = 1e9 + 7;int waysToStep(int n){//处理边界情况:if (n == 1 || n == 2)return n;if (n == 3)return 4;//创建dp表vector<int> dp(n + 1);//初始化dp[1] = 1, dp[2] = 2, dp[3] = 4;//填表for (int i = 4; i <= n; i++){//结果可能很大要进去取模dp[i] = ((dp[i - 1] + dp[i - 2]) % MOD + dp[i - 3]) % MOD;}//返回return dp[n];}
};Leetcode 测试结果: 
3 、746. 使用最小花费爬楼梯
给你一个整数数组
cost,其中cost[i]是从楼梯第i个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。你可以选择从下标为
0或下标为1的台阶开始爬楼梯。请你计算并返回达到楼梯顶部的最低花费。
示例 1:
输入:cost = [10,15,20] 输出:15 解释:你将从下标为 1 的台阶开始。 - 支付 15 ,向上爬两个台阶,到达楼梯顶部。 总花费为 15 。示例 2:
输入:cost = [1,100,1,1,1,100,1,1,100,1] 输出:6 解释:你将从下标为 0 的台阶开始。 - 支付 1 ,向上爬两个台阶,到达下标为 2 的台阶。 - 支付 1 ,向上爬两个台阶,到达下标为 4 的台阶。 - 支付 1 ,向上爬两个台阶,到达下标为 6 的台阶。 - 支付 1 ,向上爬一个台阶,到达下标为 7 的台阶。 - 支付 1 ,向上爬两个台阶,到达下标为 9 的台阶。 - 支付 1 ,向上爬一个台阶,到达楼梯顶部。 总花费为 6 。提示:
2 <= cost.length <= 10000 <= cost[i] <= 999
a、解题思路
这里我们要注意到达楼顶,应该是const数组最后一个位置的下一个位置
这里我们有二种思路:
思路一:
1、转态表示
以i位置为结尾,正好是楼顶,所以我们认为:
dp[i]表示:到达i位置时,最小花费
2、状态转移方程
根据最近的一个位置划分
先到达i-1的位置,然后支付const[i-1],走一步, 花费:dp[i-1]+cost[i-1]
先到达i-2的位置,然后支付const[i-2],走一步, 花费:dp[i-2]+cost[i-2]
所以dp[i] =min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
3、初始化
保证dp表不越界就好dp[0]=dp[1]=0;
4、 填表顺序
从左往右
5、返回值
dp[n]
思路2:
1、转态表示
以i位置为起点,到达楼顶,所以我们认为:
dp[i]表示:从i位置出发到达楼顶,此时最小花费
2、状态转移方程
根据最近的一个位置划分
- 支付const[i],往后走一步, 从i+1位置出发到楼顶,花费:dp[i+1]+cost[i]
- 支付const[i],往后走二步, 从i+2位置出发到楼顶,花费:dp[i+2]+cost[i]
所以dp[i] =min(dp[i+1]+cost[i],dp[i+2]+cost[i]);
3、初始化
保证dp表不越界就好dp[n-1]=cost[n-1],dp[n-2]=cost[n-2];
4、 填表顺序
从右往左
5、返回值
min(dp[0],dp[1]);
b、代码
这里有二种解题思路:
思路一:
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {//处理边界情况int n = cost.size();if(n==0||n==1)return cost[n];//创建dp表vector<int> dp(n+1);//填表for(int i = 2;i<=n;i++){dp[i] =min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);}//返回return dp[n];}
}; Leetcode 测试结果: 
解法二:
class Solution {
public:int minCostClimbingStairs(vector<int>& cost){int n = cost.size();//创建dp表vector<int> dp(n+1);//初始化dp[n-1]=cost[n-1],dp[n-2]=cost[n-2];//填表for(int i = n-3;i>=0;i--){dp[i] = min(dp[i+1]+cost[i],dp[i+2]+cost[i]);}//返回return min(dp[0],dp[1]);}
};Leetcode 测试结果:

4、解码方法
一条包含字母
A-Z的消息通过以下映射进行了 编码 :'A' -> "1" 'B' -> "2" ... 'Z' -> "26"要 解码 已编码的消息,所有数字必须基于上述映射的方法,反向映射回字母(可能有多种方法)。例如,
"11106"可以映射为:
"AAJF",将消息分组为(1 1 10 6)"KJF",将消息分组为(11 10 6)注意,消息不能分组为
(1 11 06),因为"06"不能映射为"F",这是由于"6"和"06"在映射中并不等价。给你一个只含数字的 非空 字符串
s,请计算并返回 解码 方法的 总数 。题目数据保证答案肯定是一个 32 位 的整数。
示例 1:
输入:s = "12" 输出:2 解释:它可以解码为 "AB"(1 2)或者 "L"(12)。示例 2:
输入:s = "226" 输出:3 解释:它可以解码为 "BZ" (2 26), "VF" (22 6), 或者 "BBF" (2 2 6) 。示例 3:
输入:s = "06" 输出:0 解释:"06" 无法映射到 "F" ,因为存在前导零("6" 和 "06" 并不等价)。提示:
1 <= s.length <= 100s只包含数字,并且可能包含前导零。
a、解题思路
看我们题目后,根据经验此题位动态规划解题
1、转态表示
首先我们想以i位置为结尾表示什么
dp[i]表示:以i位置结尾的时候,解码的方法有多少种
2、状态转移方程
根据最近的一个位置划分
让s[i]单独解码的时候,假设a=s[i]
- 成功,a!='0'(或者说是a>='1'&&a<='9'),解码的种类有dp[i-1]种
- 失败为0
让s[i-1]和s[i]组合进行解码 假设组合为b
- 成功b>='10'&&b<='26',解码的种类有dp[i-2]种
- 失败为0
有同学可能会想为什么不让dp[i]和dp[i+1]进行组合,但是大家 要明白,填表到dp[i]的时候,我们是知道dp[i-1]有多少种解码,但是我们不知道dp[i+1]有多少种解码。
所以状态转移方法为
单独解码
dp[i] +=dp[i-1];
组合解码
dp[i]=dp[i-2];
3、初始化
保证dp表
dp[0] = s[0]!='0';if(s[0]!='0'&&s[1]!='0') dp[1] +=dp[0];//这里我们还要把组合转换为数字进行判断int t = (s[0]-'0')*10+(s[1]-'0');if(t>=10&&t<=26) dp[1] +=1;4、 填表顺序
从左往右
5、返回值
dp[n-1]
b、代码
class Solution {
public:int numDecodings(string s){//创建dp表int n = s.size();vector<int> dp(n);//初始化dp[0] = s[0]!='0';//处理边界情况if(n==1) return dp[0];//单解码if(s[0]!='0'&&s[1]!='0') dp[1] +=dp[0];//组合起来int t = (s[0]-'0')*10+(s[1]-'0');if(t>=10&&t<=26) dp[1] +=1;//填表for(int i = 2;i<n;i++){//单解码if(s[i]!='0') dp[i] +=dp[i-1];//双解码int t = (s[i-1]-'0')*10+(s[i]-'0');if(t>=10&&t<=26) dp[i] +=dp[i-2];}//返回return dp[n-1];}
};Leetcode 测试结果:

c、代码优化
不知道大家分发现没,我们在初始化的代码和填表的代码,有着非常相似的特色,那我们能不能进行优化呢?
其实是可以的,多一个数组的空间就可以了。

简单的理解就是,把初始化的过程和填表合并了。但要注意二个问题:
那个虚拟节点dp[0]填写多少?后面大家做都了这种题,很多情况下都是填写0但,但是这里却是填写dp[0]=1;
为什么了,因为我们这里要保证后面填写的正确
比如:在进双解码的时候dp[i]+=dp[i-2],如何i=2时候,这里我们吧dp[0]初始化为0就会漏掉这种情况。
下标映射关系如上图。
class Solution {
public:int numDecodings(string s){//创建dp表int n = s.size();vector<int> dp(n+1);//初始化dp[0] = 1;//保证后面的填表的正确性//处理边界情况dp[1] = s[1-1]!='0';if(n==1) return dp[1];//填表for(int i = 2;i<=n;i++){//单解码if(s[i-1]!='0') dp[i] +=dp[i-1];//双解码int t = (s[i-2]-'0')*10+(s[i-1]-'0');if(t>=10&&t<=26) dp[i] +=dp[i-2];}//返回return dp[n];}
};Leetcode 测试结果:

5、不同路径(medium)
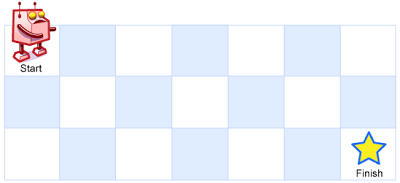
一个机器人位于一个
m x n网格的左上角 (起始点在下图中标记为 “Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
输入:m = 3, n = 7 输出:28示例 2:
输入:m = 3, n = 2 输出:3 解释: 从左上角开始,总共有 3 条路径可以到达右下角。 1. 向右 -> 向下 -> 向下 2. 向下 -> 向下 -> 向右 3. 向下 -> 向右 -> 向下示例 3:
输入:m = 7, n = 3 输出:28示例 4:
输入:m = 3, n = 3 输出:6提示:
1 <= m, n <= 100- 题目数据保证答案小于等于
2 * 109
a、解题思路
看我们题目后,根据经验此题位动态规划解题
1、转态表示
首先我们想以i,j位置为结尾表示什么
dp[i][j表示:以i,j位置结尾的时候,机器人到这里有多少条路径
2、状态转移方程
根据最近的一个位置划分

我要求到[i,j] 路径,本质上就是求dp[i - 1][j] + dp[i][j - 1]的路径和
所以状态转移方法为
dp[i][j] = dp[i-1][j]+dp[i][j-1];
3、初始化

这里我们要初始化,就是在二维数组多开一行和一列,但我们要思路多开的行列填什么呢(一切都是为了填表走服务)?,很明显,在根据dp[i][j] = dp[i-1][j]+dp[i][j-1];填写表格的时候,走一步就到终点,那最外层从从到都应该填1(dp[i][j表示:以i,j位置结尾的时候,机器人到这里有多少条路径),为达到这不目的,应该把dp[0][1]=1其余为0。
4、 填表顺序
从上往下填写每一行,每一行都是从左往又开始填写
5、返回值
dp[m][n]
b、代码
class Solution {
public:int uniquePaths(int m, int n){//创建二维dp表vector<vector<int>> dp(m + 1, vector<int>(n + 1));//初始化dp[0][1] = 1;//填表for (int i = 1; i <= m; i++){for (int j = 1; j <= n; j++){dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m][n];}
}; Leetcode 测试结果: 
相关文章:

[动态规划]---part1
前言 作者:小蜗牛向前冲 专栏:小蜗牛算法之路 专栏介绍:"蜗牛之道,攀登大厂高峰,让我们携手学习算法。在这个专栏中,将涵盖动态规划、贪心算法、回溯等高阶技巧,不定期为你奉上基础数据结构…...
)
java 关于 Object 类中的 wait 和 notify 方法。(生产者和消费者模式!)
4、关于 Object 类中的 wait 和 notify 方法。(生产者和消费者模式!) 第一:wait 和 notify 方法不是线程对象的方法,是 java 中任何一个 java 对象都有的方法,因为这两个方法是 Object 类中自带的。 wait 方…...
YOLOv8姿态估计实战:训练自己的数据集
课程链接:https://edu.csdn.net/course/detail/39355 YOLOv8 基于先前 YOLO 版本的成功,引入了新功能和改进,进一步提升性能和灵活性。YOLOv8 同时支持目标检测和姿态估计任务。 本课程以熊猫姿态估计为例,将手把手地教大家使用C…...
【海贼王的数据航海:利用数据结构成为数据海洋的霸主】链表—双向链表
目录 往期 1 -> 带头双向循环链表(双链表) 1.1 -> 接口声明 1.2 -> 接口实现 1.2.1 -> 双向链表初始化 1.2.2 -> 动态申请一个结点 1.2.3 -> 双向链表销毁 1.2.4 -> 双向链表打印 1.2.5 -> 双向链表判空 1.2.6 -> 双向链表尾插 1.2.7 -&…...

做测试还是测试开发,选职业要慎重!
【软件测试面试突击班】2024吃透软件测试面试最全八股文攻略教程,一周学完让你面试通过率提高90%!(自动化测试) 突然发现好像挺多人想投测开和测试的,很多人面试的时候也会被问到这几个职位的区别,然后有测…...

Java面试题总结200道(二)
26、简述Spring中Bean的生命周期? 在原生的java环境中,一个新的对象的产生是我们用new()的方式产生出来的。在Spring的IOC容器中,将这一部分的工作帮我们完成了(Bean对象的管理)。既然是对象,就存在生命周期,也就是作用…...
面试数据库篇(mysql)- 03MYSQL支持的存储引擎有哪些, 有什么区别
存储引擎就是存储数据、建立索引、更新/查询数据等技术的实现方式 。存储引擎是基于表的,而不是基于库的,所以存储引擎也可被称为表类型。 MySQL体系结构 连接层服务层引擎层存储层 存储引擎特点 InnoDB MYSQL支持的存储引擎有哪些, 有什么区别 ? my…...

MySQL深入——25
Join语句如何优化? Join语句的两种算法,分别为Index Nested-Loop Join和Block Nested-Loop Join NLJ在大表Join当中还不错,但BNL在大表join时性能就差很多,很耗CPU资源。 如何优化这两个算法 创建t1,t2算法,在t1中…...

Docker运行时安全之道: 保障容器环境的安全性
引言 Docker作为容器化技术的领军者,为应用部署提供了灵活性和便捷性。然而,在享受这些优势的同时,必须重视Docker运行时的安全性。本文将深入研究一些关键的Docker运行时安全策略,以确保你的容器环境在生产中得到有效的保护。 1. 使用最小特权原则 保持容器以最小权限运…...
前后端分离项目Docker部署指南(上)
目录 前言 一.搭建局域网 1.搭建net-ry局域网,用于部署若依项目 2.注意点 二.安装redis 创建目录 将容器进行挂载 编辑 测试是否安装成功 编辑 三. 安装MySQL 创建文件夹 上传配置文件并且修改 .启动MySQL容器服务 充许远程连接 四.部署后端 使用…...

ARM 架构下国密算法库
目录 前言GmSSL编译环境准备下载 GmSSL 源码编译 GmSSL 源码SM4 对称加密算法SM2 非对称加密算法小结前言 在当前的国际形式下,国替势不可挡。操作系统上,银河麒麟、统信 UOS、鸿蒙 OS 等国产系统开始发力,而 CPU 市场,也是百花齐放,有 龙芯(LoongArch架构)、兆芯(X86…...

源码的角度分析Vue2数据双向绑定原理
什么是双向绑定 我们先从单向绑定切入,其实单向绑定非常简单,就是把Model绑定到View,当我们用JavaScript代码更新Model时,View就会自动更新。那么双向绑定就可以从此联想到,即在单向绑定的基础上,用户更新…...

动态规划(算法竞赛、蓝桥杯)--树形DP树形背包
1、B站视频链接:E18 树形DP 树形背包_哔哩哔哩_bilibili #include <bits/stdc.h> using namespace std; const int N110; int n,V,p,root; int v[N],w[N]; int h[N],to[N],ne[N],tot; //邻接表 int f[N][N];void add(int a,int b){to[tot]b;ne[tot]h[a];h[a…...
electron打包前端项目
1.npm run build 打包项目文件到disk文件夹 2.安装electron:npm install electron 打开后进到/dist里面 然后把这个项目的地址配置环境变量 配置环境变量:在系统变量的path中添加进去 配置成功后,electron -v看看版本。 3.创建主程序的入口文件main.…...

2.1基本算法之枚举7647:余数相同问题
已知三个正整数 a,b,c。 现有一个大于1的整数x,将其作为除数分别除a,b,c,得到的余数相同。 请问满足上述条件的x的最小值是多少? 数据保证x有解 #include<bits/stdc.h>//万能头 using…...

求最短路径之迪杰斯特拉算法
对fill用法的介绍 1.用邻接矩阵实现 const int maxn100; const int INF100000000;//无穷大,用来初始化边 int G[maxn][maxn];//用邻接矩阵存储图的信息 int isin[maxn]{false};//记录是否已被访问 int minDis[maxn];//记录到顶点的最小距离void Dijkstra(int s,in…...

python大学社团管理系统开发文档
项目介绍 一直想做一款大学社团管理系统,看了很多优秀的开源项目但是发现没有合适的。于是利用空闲休息时间开始自己写了一套管理系统。 在线体验 代码下载:https://github.com/geeeeeeeek/python_team演示地址:http://team.gitapp.cn/ &…...

leetcode 1328.破坏回文串
题目链接LeetCode1328 1.题目 给你一个由小写英文字母组成的回文字符串 palindrome ,请你将其中 一个 字符用任意小写英文字母替换,使得结果字符串的 字典序最小 ,且 不是 回文串。 请你返回结果字符串。如果无法做到,则返回一个…...
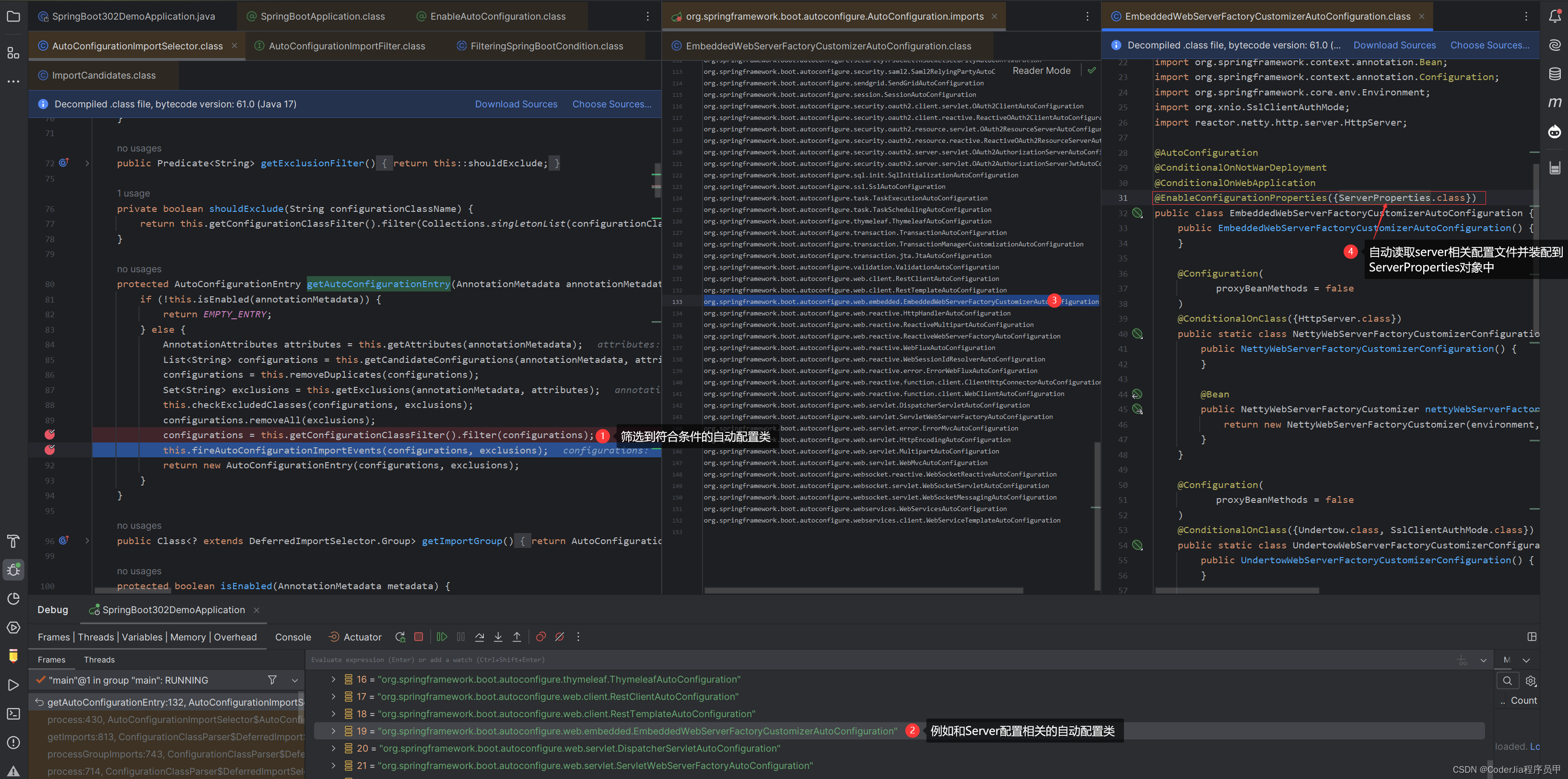
重学SpringBoot3-自动配置机制
重学SpringBoot3-自动配置机制 引言Spring Boot 自动配置原理示例:Spring Boot Web 自动配置深入理解总结相关阅读 引言 Spring Boot 的自动配置是其最强大的特性之一,它允许开发者通过最少的配置实现应用程序的快速开发和部署。这一切都得益于 Spring …...
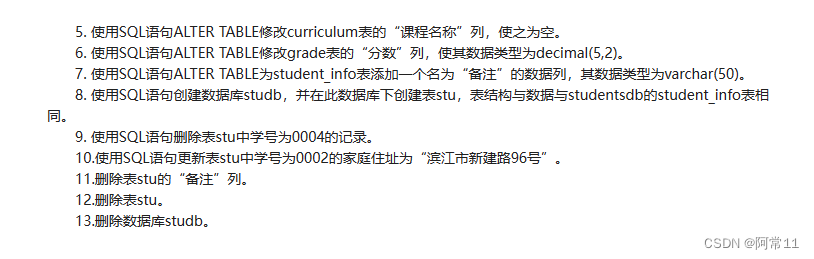
sql基本语法+实验实践
sql语法 注释: 单行 --注释内容# 注释内容多行 /* 注释内容 */数据定义语言DDL 查询所有数据库 show databases;注意是databases而不是database。 查询当前数据库 select database();创建数据库 create database [if not exists] 数据库名 [default charset 字符…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...