WPF中如何设置自定义控件(二)
前一篇文章中简要讲解了圆角按钮、圆形按钮的使用,以及在windows.resource和app.resource中设置圆角或圆形按钮的样式。
这篇主要讲解Polygon(多边形)、Ellipse(椭圆)、Path(路径)这三个内容。
Polygon
我们先看一下的源码:
namespace System.Windows.Shapes
{
public sealed class Polygon : Shape
{
public static readonly DependencyProperty PointsProperty = DependencyProperty.Register("Points", typeof(PointCollection), typeof(Polygon), new FrameworkPropertyMetadata((object)new FreezableDefaultValueFactory((Freezable)PointCollection.get_Empty()), FrameworkPropertyMetadataOptions.AffectsMeasure | FrameworkPropertyMetadataOptions.AffectsRender));
public static readonly DependencyProperty FillRuleProperty = DependencyProperty.Register("FillRule", typeof(FillRule), typeof(Polygon), (PropertyMetadata)new FrameworkPropertyMetadata(FillRule.EvenOdd, FrameworkPropertyMetadataOptions.AffectsMeasure | FrameworkPropertyMetadataOptions.AffectsRender), (ValidateValueCallback)ValidateEnums.IsFillRuleValid);
private Geometry _polygonGeometry;
public PointCollection Points
{
get
{
return (PointCollection)GetValue(PointsProperty);
}
set
{
SetValue(PointsProperty, value);
}
}
public FillRule FillRule
{
get
{
return (FillRule)GetValue(FillRuleProperty);
}
set
{
SetValue(FillRuleProperty, value);
}
}
protected override Geometry DefiningGeometry => _polygonGeometry;
internal override void CacheDefiningGeometry()
{
PointCollection points = Points;
PathFigure pathFigure = new PathFigure();
if (points == null)
{
_polygonGeometry = Geometry.Empty;
return;
}
if (points.Count > 0)
{
pathFigure.StartPoint = points[0];
if (points.Count > 1)
{
Point[] array = new Point[points.Count - 1];
for (int i = 1; i < points.Count; i++)
{
array[i - 1] = points[i];
}
pathFigure.Segments.Add(new PolyLineSegment(array, isStroked: true));
}
pathFigure.IsClosed = true;
}
PathGeometry pathGeometry = new PathGeometry();
pathGeometry.Figures.Add(pathFigure);
pathGeometry.FillRule = FillRule;
_polygonGeometry = pathGeometry;
}
}
}
从源码的信息可以看到Polygon是继承自Shape的类,可用的属性只有PointsProperty、FillRuleProperty两个属性;PointsProperty是PointCollection的Point集合,而Point实质就是一个二维坐标集合,因此在Polygon的使用中Points的中的数据必须是2N个。用法如下:
<Polygon Points="100,400 200,370 180,470" Fill="#4EB1B6" /><!--多边形-->
效果图:

Ellipse
源码如下:
namespace System.Windows.Shapes
{
public sealed class Ellipse : Shape
{
private Rect _rect = Rect.Empty;
public override Geometry RenderedGeometry => DefiningGeometry;
public override Transform GeometryTransform => Transform.Identity;
protected override Geometry DefiningGeometry
{
get
{
if (_rect.IsEmpty)
{
return Geometry.Empty;
}
return new EllipseGeometry(_rect);
}
}
internal override int EffectiveValuesInitialSize => 13;
static Ellipse()
{
Shape.StretchProperty.OverrideMetadata(typeof(Ellipse), new FrameworkPropertyMetadata(Stretch.Fill));
}
protected override Size MeasureOverride(Size constraint)
{
if (base.Stretch == Stretch.UniformToFill)
{
double width = constraint.Width;
double height = constraint.Height;
if (double.IsInfinity(width) && double.IsInfinity(height))
{
return GetNaturalSize();
}
width = ((!double.IsInfinity(width) && !double.IsInfinity(height)) ? Math.Max(width, height) : Math.Min(width, height));
return new Size(width, width);
}
return GetNaturalSize();
}
protected override Size ArrangeOverride(Size finalSize)
{
double strokeThickness = GetStrokeThickness();
double num = strokeThickness / 2.0;
_rect = new Rect(num, num, Math.Max(0.0, finalSize.Width - strokeThickness), Math.Max(0.0, finalSize.Height - strokeThickness));
switch (base.Stretch)
{
case Stretch.None:
{
double num4 = (_rect.Width = (_rect.Height = 0.0));
break;
}
case Stretch.Uniform:
if (_rect.Width > _rect.Height)
相关文章:

WPF中如何设置自定义控件(二)
前一篇文章中简要讲解了圆角按钮、圆形按钮的使用,以及在windows.resource和app.resource中设置圆角或圆形按钮的样式。 这篇主要讲解Polygon(多边形)、Ellipse(椭圆)、Path(路径)这三个内容。 Polygon 我们先看一下的源码: namespace System.Windows.Shapes { pu…...

【C++】每周一题——2024.3.3
题目 Cpp 【问题描述】 字符环(来源:NOI题库)。有两个由字符构成的环,请写一个程序,计算这两个字符环上最长公共字符串的长度。例如,字符串“ABCEFAGADEGKABUVKLM”的首尾连在一起,构成一个环&a…...
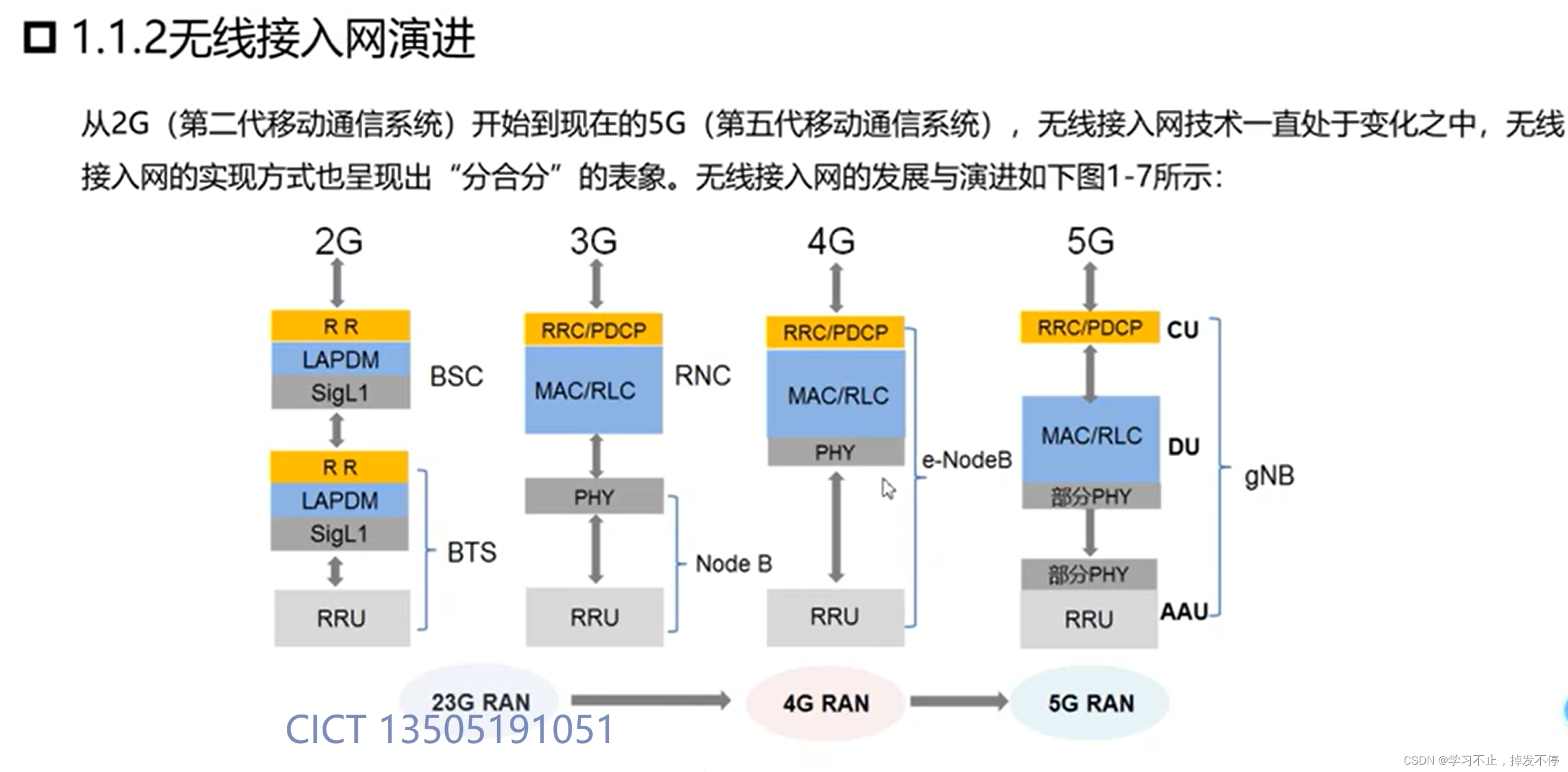
5G网络架构与组网部署01--5G网络架构的演进趋势
目录 1. 5G网络架构的演进趋势 1.1 5G移动通信系统整体架构 1.2 4G移动通信系统整体架构 1.3 4G与5G移动通信系统整体架构对比 1.4 核心网架构演进 1.5 无线接入网演进 1. 整体架构组成:接入网,核心网 2. 5G网络接入网和核心网对应的网元ÿ…...

2023全球软件开发大会-上海站:探索技术前沿,共筑未来软件生态(附大会核心PPT下载)
随着信息技术的迅猛发展,全球软件开发大会(QCon)已成为软件行业最具影响力的年度盛会之一。2023年,QCon再次来到上海,汇聚了众多业界精英、技术领袖和开发者,共同探讨软件开发的最新趋势和实践。 一、大会…...

C#插入排序算法
插入排序实现原理 插入排序算法是一种简单、直观的排序算法,其原理是将一个待排序的元素逐个地插入到已经排好序的部分中。 具体实现步骤如下 首先咱们假设数组长度为n,从第二个元素开始,将当前元素存储在临时变量temp中。 从当前元素的前一…...
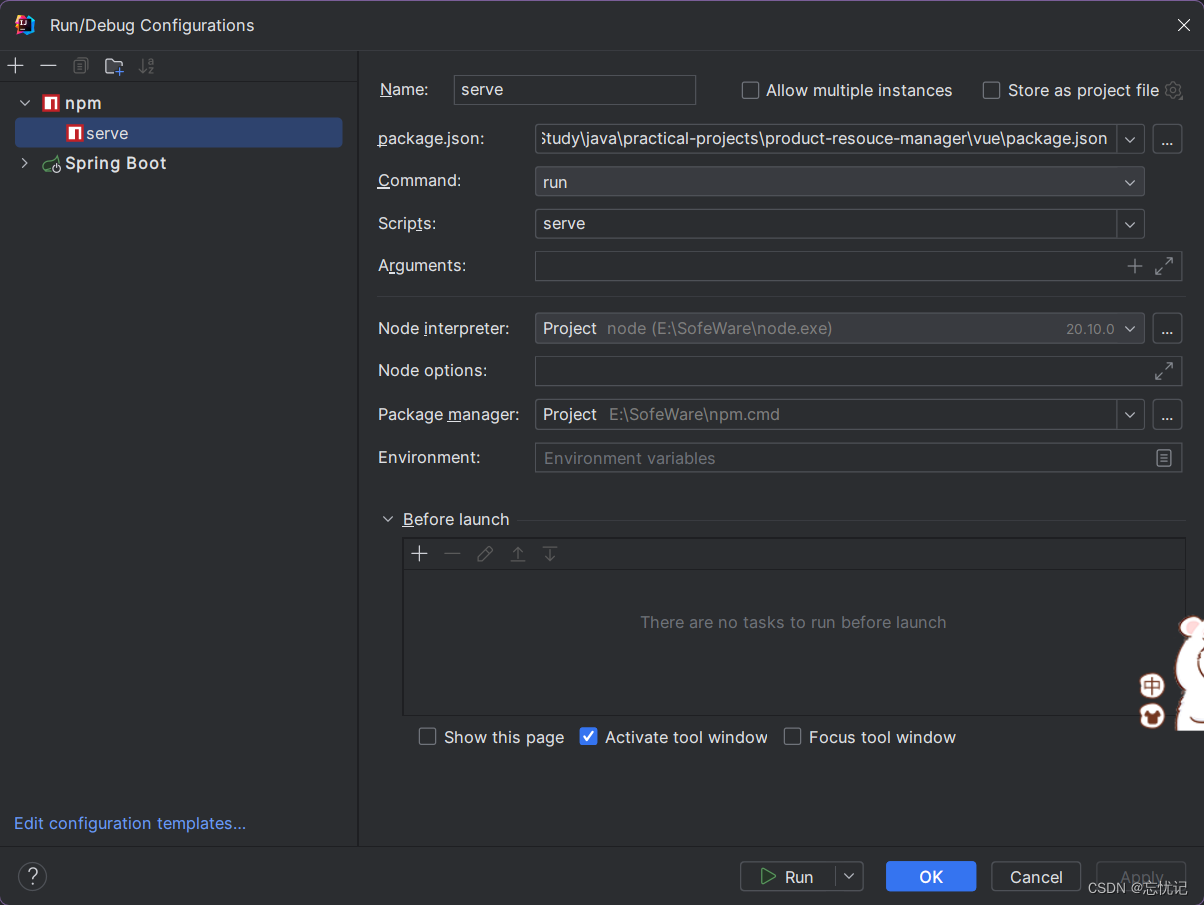
快速搭建Vue前端框架
快速搭建Vue前端框架 安装Vue Vue官方安装过程:https://cli.vuejs.org/zh/guide/installation.html 二.创建Vue工程 2.2 安装淘宝镜像 安装淘宝镜像(会让你安装Vue的速度加快): npm config set registry https://registry.npm.taobao.or…...

TS中private和protected的区别
在 TypeScript 中,private 和 protected 是两种访问修饰符,用于限制类成员(如属性、方法等)的可见性和可访问性。它们的主要区别在于访问权限的宽松程度。 1. private 当一个类的成员被标记为 private 时,它只能在该…...

虚拟机Hyper-V操作记录
问题1:安装Hyper-V,虚拟机监控程序无法打钩,提示该固件的虚拟化支持被禁用 主板型号:华硕ASUS ROG STRIX Z390-E GAMING 解决方法:进入BIOS,Advanced/CPU Configuration/Intel(VMX) Virtualization Technol…...
)
90. 子集 II(力扣LeetCode)
文章目录 90. 子集 II题目描述回溯算法 90. 子集 II 题目描述 给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的子集(幂集)。 解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 …...

202435读书笔记|《半小时漫画中国史》——读点经济学与历史,生活更美好,趣味烧脑土地制度、商鞅变法、华丽丽的丝绸之路这里都有
202435读书笔记|《半小时漫画中国史》——读点经济学与历史,生活更美好,趣味烧脑土地制度、商鞅变法、华丽丽的丝绸之路这里都有 1. 土地政策、度量衡及税收2. 商鞅变法3. 西汉经济4. 西汉盐铁大辩论5. 西汉丝绸之路 《半小时漫画中国史:经济…...

2023下半年主品牌锋芒依旧,江南布衣打破既定天花板?
在过去的2023年里,服装板块令人意外的领涨消费大盘,国家统计局数据显示,上半年服装零售额同比增长12.8%,远超商品零售大盘的增速6.8%。 整体表现强劲的同时,“局部”表现是否也尽如人意。近日,作为时尚服装…...
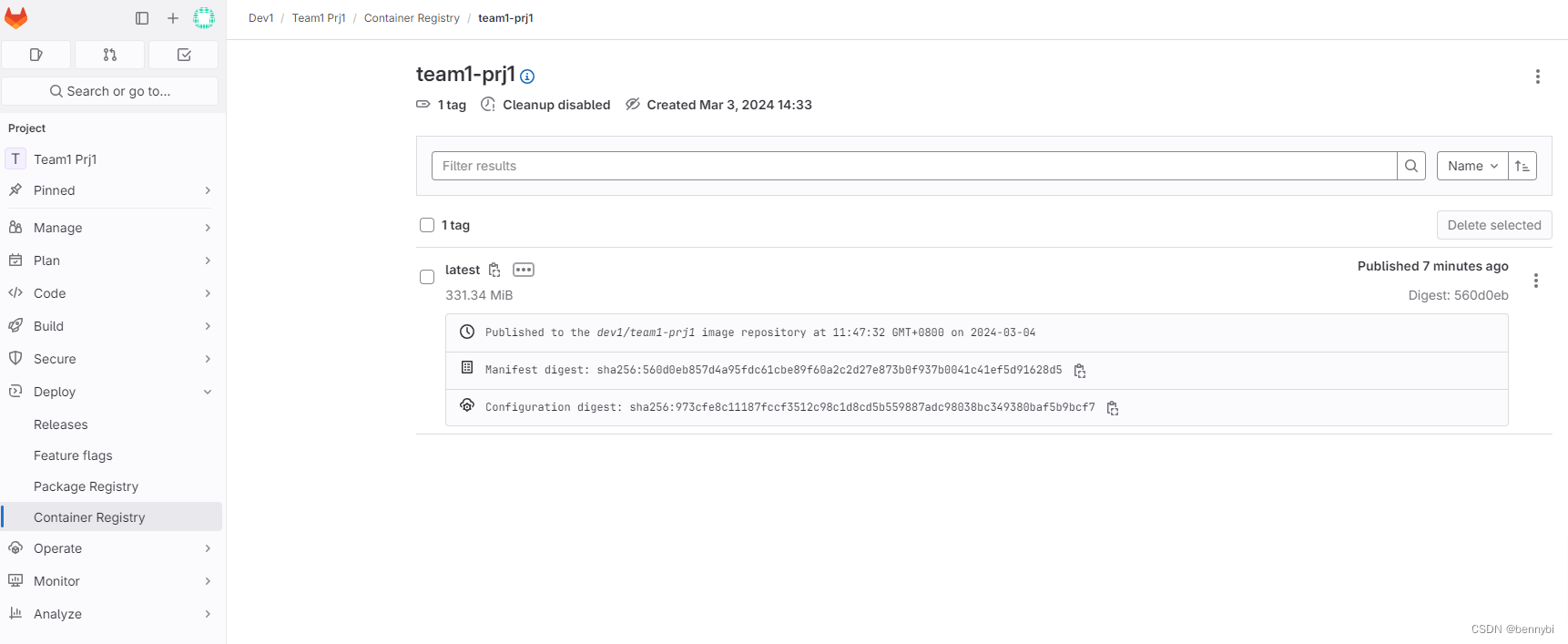
Gitlab: PHP项目CI/CD实践
目录 1 说明 2 CI/CD 2.1 部署方式一:增量部署 2.1.1 目标服务器准备 2.2.2 Gitlab及Envoy脚本 2.2 部署方式二:镜像构建与部署 2.2.1 推送到私有化容器仓库 准备工作 脚本 要点 2.2.2 推送到hub.docker.com 准备工作 脚本 3 参考&#x…...
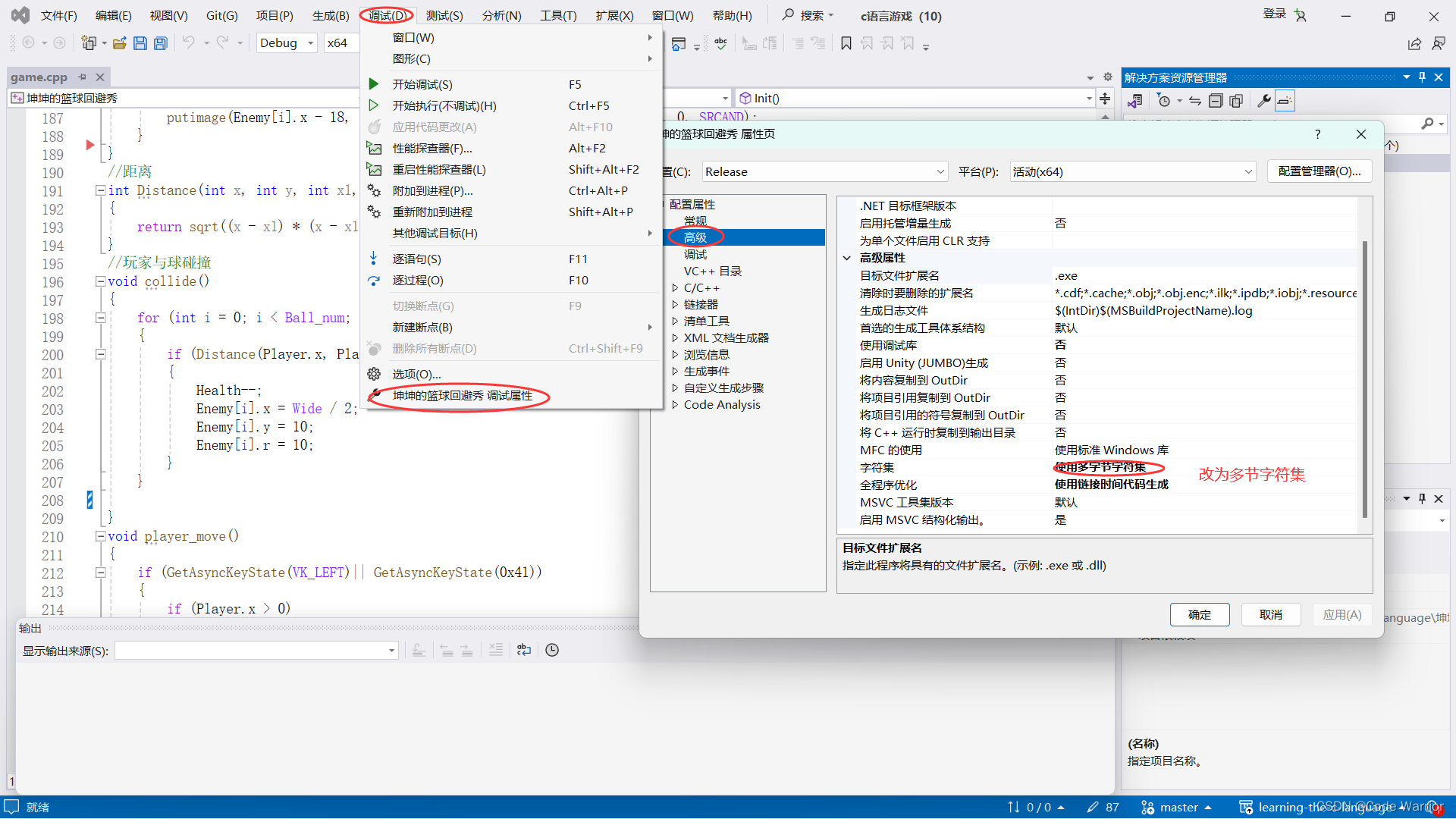
c语言游戏实战(10):坤坤的篮球回避秀
前言: 这款简易版的球球大作战是博主耗时两天半完成的,玩家需要控制坤坤在游戏界面上移动,来躲避游戏界面上方不断掉下来的篮球。本游戏使用C语言和easyx图形库编写,旨在帮助初学者了解游戏开发的基本概念和技巧。 在开始编写代…...
初学arp欺骗
首先准备一台靶机这里用虚拟机的win10 已知网关与ip地址(怕误伤) 现在返回kali从头开始 首先探测自己的网关 然后扫内网存活的ip 发现有3台 用nmap扫一下是哪几台 成功发现我们虚拟机的ip 现在虚拟机可以正常访问网络 接下来直接开梭 ip网关 返回虚拟机…...

ftp几个常见错误问题及解决办法
1、无法上传网页,FTP故障-提示“无法连接服务器”错误。 问题出现原因:FTP客户端程序设置问题,客户上网线路问题,ftp服务器端问题。 处理方法:建议客户使用CUTPFTP软件来上传客户的网页,在“F…...
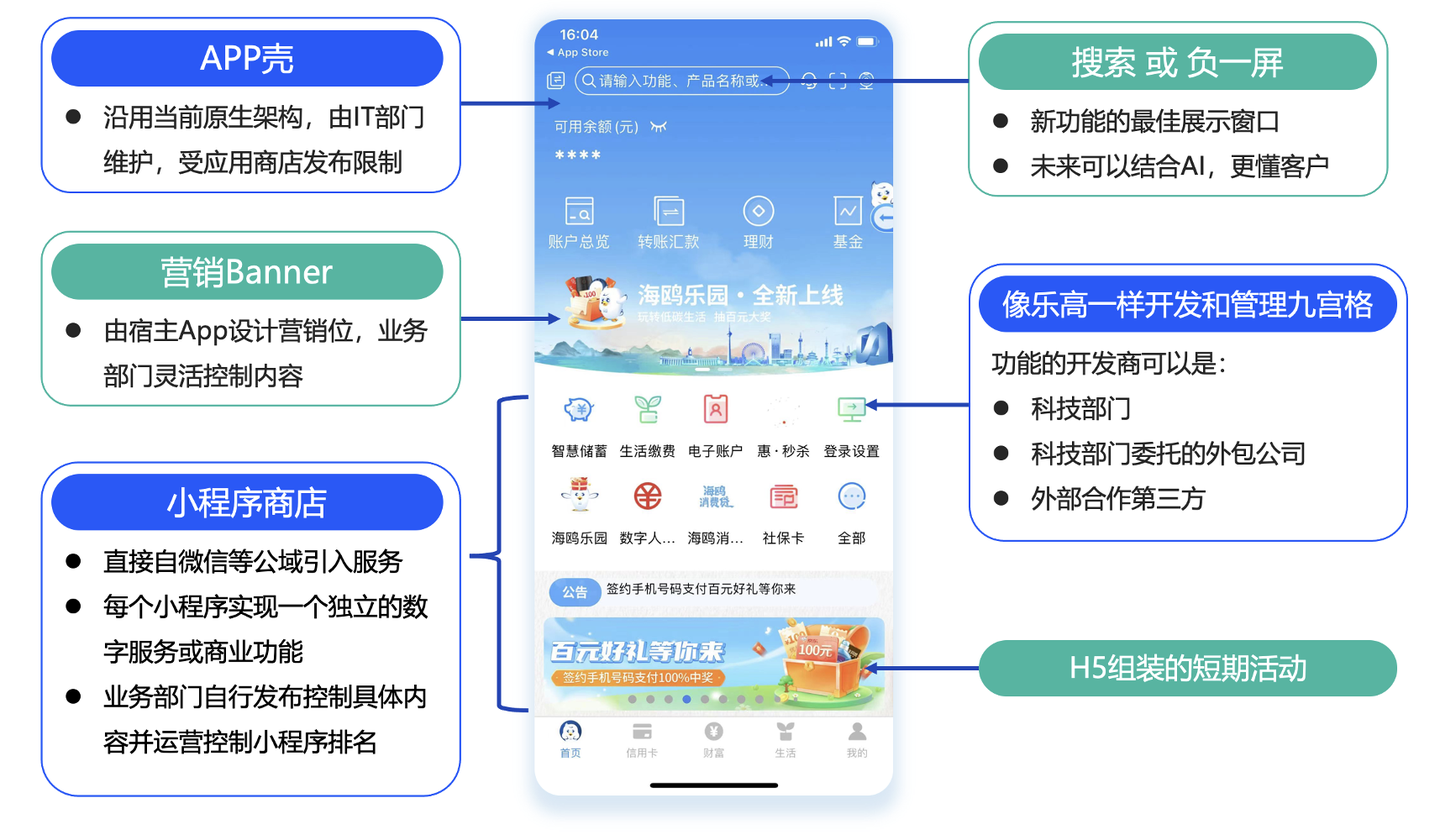
鸿蒙App开发新思路:小程序转App
国家与国家之间错综复杂,在谷歌的安卓操作系统“断供”后,鸿蒙系统的市场化&独立化的道路便显而易见了。 2024年1月18日,华为宣布,不再兼容安卓的“纯血鸿蒙”--HarmonyOS NEXT鸿蒙星河版最终面世,并与2024年Q4正…...
)
C++17之std::invoke: 使用和原理探究(全)
C进阶专栏:http://t.csdnimg.cn/5mV9r 目录 1.概述 2.辅助类 3.原理分析 4.总结 1.概述 在之前的 C 版本中,要调用不同类型的可调用对象,需要使用不同的语法,例如使用函数调用运算符 () 来调用函数或函数指针,使用…...
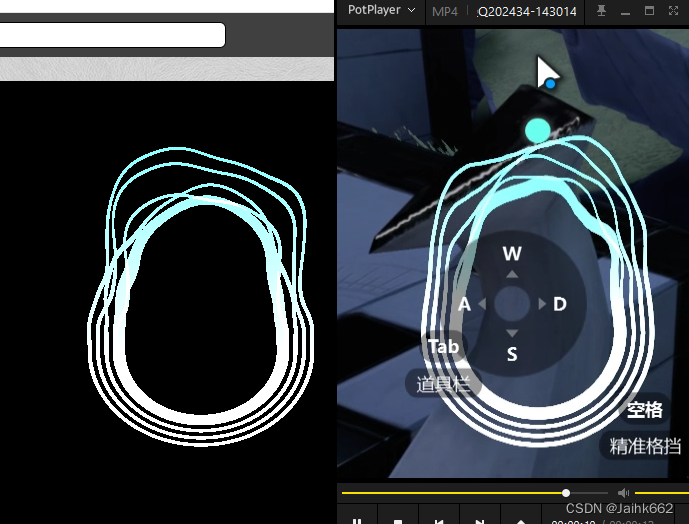
shadertoy 游戏《来自星尘》摇杆复刻
正确的做法应该是上 noise 而不是叠加 sin 波,不过如果不想麻烦的话叠波还是一个不错的选择:整体效果如下,已经非常形似 直接上链接:Shader - Shadertoy BETA float radiusScale 0.9; float variation(vec2 v1, vec2 v2, float …...
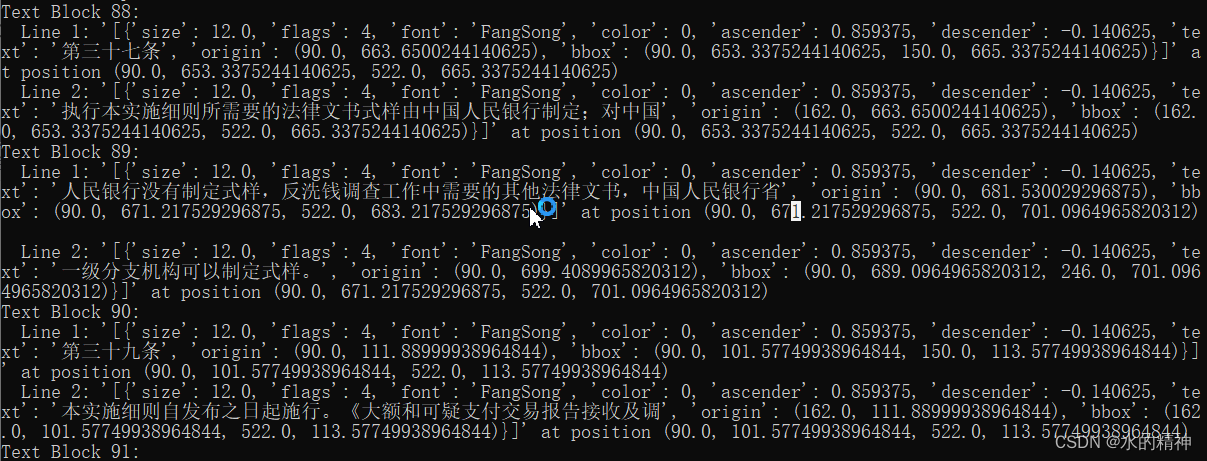
获取PDF中的布局信息——如何获取段落
PDF解析是极其复杂的问题。不可能靠一个工具解决全部问题,尤其是五花八门,格式不统一的PDF文件。除非有钞能力。如果没有那就看看可以分为哪些问题。 提取文本内容,提取表格内容,提取图片。我认为这些应该是分开做的事情。python有…...

Laya2.13.3在Web条件下使用键盘控制相机移动
需求:在Laya开发时,常常没法移动相机来观察场内的环境,故制作一个移动相机的脚本来是实现此功能,目前先使用键盘后续会添加鼠标控制移动旋转等功能。 onEnable(){this.camera new Laya.Camera(0, 0.1, 100);this._tempVector3 n…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...
