0103深度优先搜索和单点连通-无向图-数据结构和算法(Java)
文章目录
- 1.1 走迷宫
- 1.2 图的深度优先搜索实现
- 1.3 算法分析及性能
- 1. 4 单点连通性
- 后记
1.1 走迷宫
简单的迷宫,如下图1.1-1所示:

探索迷宫而不迷路,我们需要:
- 选择一条没有标记过的通道,在你走过的路上铺一条绳子;
- 标记所有你第一次路过的路口和通道;
- 当来到一个标记过的路口时(用绳子)回退到上一个路口;
- 当回退的路口已没有可走的通道时继续回退。
绳子可以保证总能找到一条出路,标记能保证你不会两次经过同一条通道或者路口。我们把上迷宫,用等价的图来代替,如下图1.1-2所示:
1.2 图的深度优先搜索实现
图的遍历算法非递归代码如下:
import java.util.Map;/*** key-value pair 类* @author: Administrator* @createTime: 2023/03/04 21:49*/
public final class Entry<K, V> implements Map.Entry<K, V>{private K key;private V value;public Entry(K key, V value) {this.key = key;this.value = value;}@Overridepublic K getKey() {return key;}@Overridepublic V getValue() {return value;}@Overridepublic V setValue(V value) {V oldValue = value;this.value = value;return oldValue;}
}/**===========*/import com.gaogzhen.datastructure.stack.Stack;
import edu.princeton.cs.algs4.Graph;import java.util.Iterator;/*** 单点连通性* @author: Administrator* @createTime: 2023/03/03 19:58*/
public class DepthFirstSearch {/*** 顶点是否标记*/private boolean[] marked;/*** 与指定顶点连通的顶点总数*/private int count;/*** 图*/private Graph graph;/*** 起点*/private int s;public DepthFirstSearch(Graph graph, int s) {this.graph = graph;this.s = s;check(s);marked = new boolean[graph.V()];dfs();}/*** 搜索图g中与起点v连通的所有顶点*/private void dfs() {Stack<Entry<Integer, Iterator<Integer>>> path = new Stack<>();// marked[v] = true;if (!marked[s]) {marked[s] = true;count++;Iterable<Integer> iterable = graph.adj(s);Iterator<Integer> it;if (iterable != null && (it = iterable.iterator()) != null){path.push(new Entry<>(s, it));}}while (!path.isEmpty()) {Entry<Integer, Iterator<Integer>> entry = path.pop();int x;Iterator<Integer> it = entry.getValue();Integer f = entry.getKey();while (it.hasNext()) {x = it.next();if (!marked[x]) {marked[x] = true;count++;if (it.hasNext()) {path.push(entry);}Iterable<Integer> iterable = graph.adj(x);if (iterable != null && (it = iterable.iterator()) != null){path.push(new Entry<>(x, it));}break;}}}}/*** 检测索引是否在范围之内* @param i 给定索引*/private void check(int i) {if (i < 0 || i > graph.V() - 1) {throw new IndexOutOfBoundsException("索引越界异常");}}/*** 判断起点是否与给定顶点x连通* @param x 给定顶点* @return*/public boolean marked(int x) {check(x);return marked[x];}/*** 返回图中与顶点想连通的顶点数* @return*/public int count() {return count;}}测试代码:
public static void testDepth() {String path = "H:\\gaogzhen\\java\\projects\\algorithm\\asserts\\maze.txt";In in = new In(path);Graph graph = new Graph(in);int s = 0;DepthFirstSearch depthFirstSearch = new DepthFirstSearch(graph, s);int t = 5;System.out.println(depthFirstSearch.marked(t));System.out.println(depthFirstSearch.count());
}
// 测试结果
true
6
1.3 算法分析及性能
知识点:
- Entry类就是一个键值对类,存在一对键值;在DepthFirstSearch中key用于存储顶点序号,value存储该顶点对应邻接顶点迭代器。
- 深度优先搜索非递归实现,主要借助栈来代替递归调用栈帧结构,已节省内存占用和提高运行效率。
算法分析:dfs()方法为该算法实现的主要方法,方法源代码以给出,这里不再赘述整体流程,着重分析下以下一个关键问题。
- 该非递归dfs方法如何保证深度优先?
- 首先我把键值对Entry起点和起点对应的邻接(连通)顶点集合迭代器压入栈中
- 外层循环开始
- 弹出栈顶元素,获取Entry的顶点及对应的邻接顶点集合迭代器
- 内层循环判断该迭代器有下一个元素即还有邻接顶点,取出一个邻接顶点。
- 判断改邻接顶点没有被标记过
- 标记数组对应顶点索引标记
- 连通顶点计数+1
- 判断迭代器还有元素,重新压入栈中
- break跳出内层循环
- 判断改邻接顶点没有被标记过
- 总结:只要邻接顶点(更深一层的顶点)没被标记过,标记之后同层迭代器压入栈中,去访问更深一层的顶点;而不是继续访问同层的顶点。
- 该dfs方法如果保证同层(同一个顶点的邻接顶点)访问全部访问完毕且只访问一次?
- 每个顶点只访问一次是标记数组marked[]索引和顶点一一对应,默认都是false未标记;标记之后不会在压入栈中,自然不会在标记一次
- 访问同层元素是通过迭代器完成的,while配合迭代hasNext,next()方法保证全部访问一边且不会重复访问。
- 深度优先算法性能如何?见下面的命题及证明。
- 这里根据上面的算法简单分析
- 完成循环判断栈不为空,那么只有未被标记的顶点及其邻接表(迭代器)会放入栈中;也就是说所有的顶点及其邻接表都会被放入栈中且不会重复
- 内层判断迭代器有元素那么所有的邻接表会被遍历一边,邻接表代表对应顶点的度数
- 结论深度优先搜索标记与起点连通的所有顶点所需的时间和顶点的度数之和成正比
命题A。深度优先搜索标记与起点连通的所有顶点所需的时间和顶点的度数之和成正比。
证明:首先,我们要证明这个算法能标记所有与起点s连通的所有顶点(且不会标记其他顶点)。算法仅通过边来寻找顶点,所以每个被标记的顶点都与s连通;反证法证明标记了所有与s连通的顶点,假设某个没有被标记的顶点w与s连通。因为s作为起点是被标记的,由s到w的任意一条路径中至少有一条边连接的两个顶点分别被标记过河没有被标记过,例如v-x。根据算法,在标记了v后比如发现x,因此这样的边不存在。
每个顶点都只会被标记一次保证了时间上限(检查标记的耗时和度数成正比)。
详细搜索轨迹,可参考算法第四版341页。
1. 4 单点连通性
连通性。给定一幅图,回答“两个给定的顶点是否连通”?或者图中有多少个连通子图等类似问题。
问题“两个给定的顶点是否连通?”等价于“两个给定的顶点间是否存在一条路径?”,也可以叫做路经检测问题。深度优先搜索解决了这个问题。
递归方法参考《算法第四版?或者书提供的jar包。
后记
如果小伙伴什么问题或者指教,欢迎交流。
❓QQ:806797785
⭐️源代码仓库地址:https://gitee.com/gaogzhen/algorithm
参考链接:
[1][美]Robert Sedgewich,[美]Kevin Wayne著;谢路云译.算法:第4版[M].北京:人民邮电出版社,2012.10.P338-P342.
相关文章:

0103深度优先搜索和单点连通-无向图-数据结构和算法(Java)
文章目录1.1 走迷宫1.2 图的深度优先搜索实现1.3 算法分析及性能1. 4 单点连通性后记1.1 走迷宫 简单的迷宫,如下图1.1-1所示: 探索迷宫而不迷路,我们需要: 选择一条没有标记过的通道,在你走过的路上铺一条绳子&…...

进销存管理系统
技术:Java等摘要:进销存管理系统是为了实现企业仓库商品管理的系统化、规范化和自动化,从而提高企业管理效率而设计开发的管理信息系统。它完全取代了过去一直用人工管理的工作方式,避免了由于管理人员手工操作上的疏忽以及管理质…...

Sonar:VSCode配置SonarLint/SonarLint连接SonarQube
需求描述 公司为项目代码配置了Sonar检测,希望在VSCode中开发项目时能够同步检测结果。 注意事项 SonarQube版本必须为7.9,否则SonarLint无法连接(GitHub-SonarLint-Wiki第一行就有说明)!!!S…...
陀螺仪小车(Forerake-Car)
项目简介:搭建一辆有arduino UNO 与rnf24l01组成的小车;手部安装由arduino nano开发板、nrf24l01、imu构成的手势控制器,利用手势控制器检测手部状态、发送信号对小车进行前进,实现基于卡尔曼滤波的MPU6050姿态结算。 准备工作&am…...

Leetcode Day5 含有重复元素集合的组合+
1、含有重复元素集合的组合 给定一个可能有重复数字的整数数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。 candidates 中的每个数字在每个组合中只能使用一次,解集不能包含重复的组合。 【题目传送门】 思…...
Mac Book pro(M1)使用总结
1、拿到电脑激活的时候,一定要记住账号密码及安全问题的答案。 2、显示隐藏文件夹: 3、显示.git或者gitignore等隐藏后缀的文件: 打开终端 defaults write com.apple.finder AppleShowAllFiles TRUE重启Finder在终端输入 killall Finder …...
QML集成JavaScript
在QML中可以使用现有的QML元素来创建页面,但QML紧密的集成了必要的JavaScript。 但QML中使用JavaScript比较严格,在QML中不可以添加或修改JavaScript全局对象成员,这样可能会使用一个未经声明的变量。 内联JavaScript 一些小型的JavaScript函…...
学习周报3.5
文章目录前言文献阅读摘要介绍方法总结相关性总结前言 本周阅读文献《Multi-step ahead probabilistic forecasting of multiple hydrological》,文献主要提出一种基于三维卷积神经网络、卷积最小门记忆神经网络和变分贝叶斯神经网络的混合深度学习模型(…...

java基础学习篇
java学习 多写(代码、笔记、文章),多练(交流、思维、技能),多分享,多提问、多思考 什么是计算机 由硬件和软件组成,广泛应用在科学计算、数据处理、自动控制,计算机辅…...

Go 语言基础语法及应用实践
Go语言是一门由Google开发的静态类型、编译型的开源编程语言,被设计成简单、高效、安全的语言。作为一门相对年轻的语言,Go语言的使用范围正在不断扩大,特别是在Web开发、云计算、容器化和分布式系统等领域越来越受到欢迎。 在本篇文章中,我们将探讨Go语言的基础语法及应用…...

C语言自定义类型---进阶
之前的文章中有结构体初阶知识的讲解,对结构体不是很了解的小伙伴可以先去去看一下结构体初阶 结构体,枚举,联合结构体结构体类型的声明特殊的声明结构的自引用结构体变量的定义和初始化结构体内存对齐 <3 <3 <3(重点)那为什么存在内…...

85.链表总结
链表总结 链表总结与进阶 抽象数据类型(ADT abstract data type)与抽象数据接口(ADI abstract data Interface) 链表实际上就是对于结构体、结构体指针和结构体内可以包含指向同类型的结构体指针不可以包含指向同类型的结构体的应…...
【博学谷学习记录】超强总结,用心分享|狂野大数据课程【DataFrame的相关API】的总结分析
操作dataFrame一般有二种操作的方式, 一种为SQL方式, 另一种为DSL方式 SQL方式: 通过编写SQL语句完成统计分析操作DSL方式: 领域特定语言 指的通过DF的特有API完成计算操作(通过代码形式)从使用角度来说: SQL可能更加的方便一些, 当适应了DSL写法后, 你会发现DSL要比SQL更加…...

粒子群优化最小二乘支持向量机SVM回归分析,pso-lssvm回归预测
目录 支持向量机SVM的详细原理 SVM的定义 SVM理论 SVM应用实例,粒子群优化最小二乘支持向量机SVM回归分析 代码 结果分析 展望 支持向量机SVM的详细原理 SVM的定义 支持向量机(support vector machines, SVM)是一种二分类模型,它的基本模型是定义在特征空间上的间隔最大…...

lavis多模态开源框架学习--安装
安装lavis安装lavis测试安装问题过程中的其他操作安装lavis 因为lavis已经发布在pypi中,所以可以直接利用pip安装 pip install salesforce-lavis测试安装 from lavis.models import model_zoo print(model_zoo) # # Architectures Types # # …...
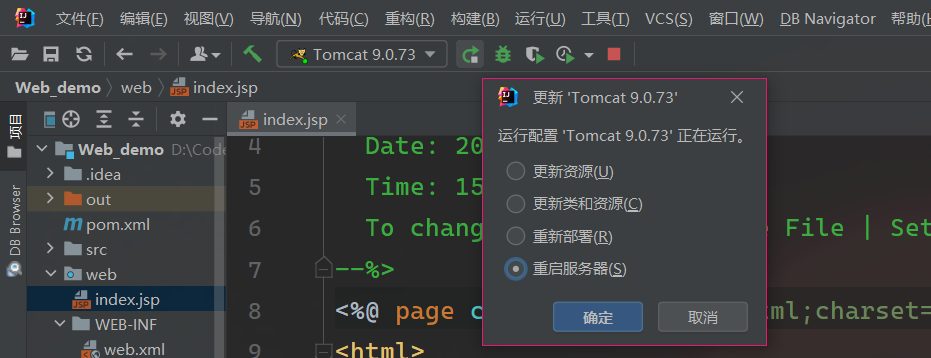
【IDEA】如何在Tomcat上创建部署第一个Web项目?
看了网上很多教程,发现或多或都缺失了一些关键步骤信息,对于新手小白很不友好,那么今天就教大家如何在Tomcat服务器(本地)上部署我们的第一个Web项目: 共分为三个部分: 1. IDEA创建Web项目&am…...
程序员画流程图的工具Draw.io
Draw.io 是一个很好用的免费流程图绘制工具,制图结果本质上是xml文件,web版和桌面版可以支持导出图像(png或者svg矢量图都可以)。你可以利用它绘制一系列的图表、图示或图形,包括流程图、UML类图、组织结构图、泳道图、E-R 图、文…...

CAPL脚本DBLookup函数动态访问CAN 报文的属性
🍅 我是蚂蚁小兵,专注于车载诊断领域,尤其擅长于对CANoe工具的使用🍅 寻找组织 ,答疑解惑,摸鱼聊天,博客源码,点击加入👉【相亲相爱一家人】🍅 玩转CANoe&…...

2022年显卡性能跑分排名表
2022年显卡性能跑分排名表(数据来源于快科技)这个版本的电脑显卡跑分榜第一的是NVIDIA GeForce RTX 3090 Ti显卡。由于显卡跑分受不同的测试环境、不同的显卡驱动版本以及不同散热设计而有所不同,所以显卡跑分会一直变化。 前二十名的台式电…...
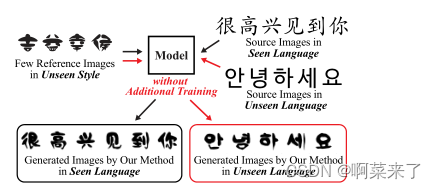
mx-font
Abstract 短镜头字体生成(FFG)方法必须满足两个目标:生成的图像既要保留目标字符的底层全局结构,又要呈现多样化的局部参考风格。现有的FFG方法旨在通过提取通用表示样式或提取多个组件样式表示来分离内容和样式。然而,以往的方法要么无法捕捉不同的本地风格,要么无法推广到…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

02.运算符
目录 什么是运算符 算术运算符 1.基本四则运算符 2.增量运算符 3.自增/自减运算符 关系运算符 逻辑运算符 &&:逻辑与 ||:逻辑或 !:逻辑非 短路求值 位运算符 按位与&: 按位或 | 按位取反~ …...
