当前位置： 首页 > news >正文

论文笔记 | Conducting research in marketing with quasi-experiments

news 2026/2/10 7:26:29

这篇论文是Journal of Marketing上的论文，讲了使用准实验来进行论文研究的一些事项。外生性识别的来源、几种准实验方法的注意点还有内生性的解决。

这篇论文对于准实验或者是平常论文的展开有一个非常友善的指导功能，可以阅读~

摘要：本文旨在通过描述使他们的工作令人信服的基本逻辑和一系列行动，扩大营销学者和那些阅读他们工作的人对准实验方法的理解。*准实验方法的目的是，在没有实验变异的情况下，确定因果关系的存在。*首先，作者探讨了如何识别有趣的环境和数据，以了解一个行为是否会对营销结果产生因果影响。其次，他们概述了如何构建一个实证战略，以确定因果经验关系。本文详细介绍了各种方法的应用，以确定一种行为如何影响营销结果，包括DID、RDD、IV、PSM、SCM和Heckman。作者强调了清楚地传达因果关系断言下的识别假设的重要性。最后，他们解释了探索行为机制——无论是个人、组织还是市场层面——实际上可以加强因果关系的论点。

外生性识别来源

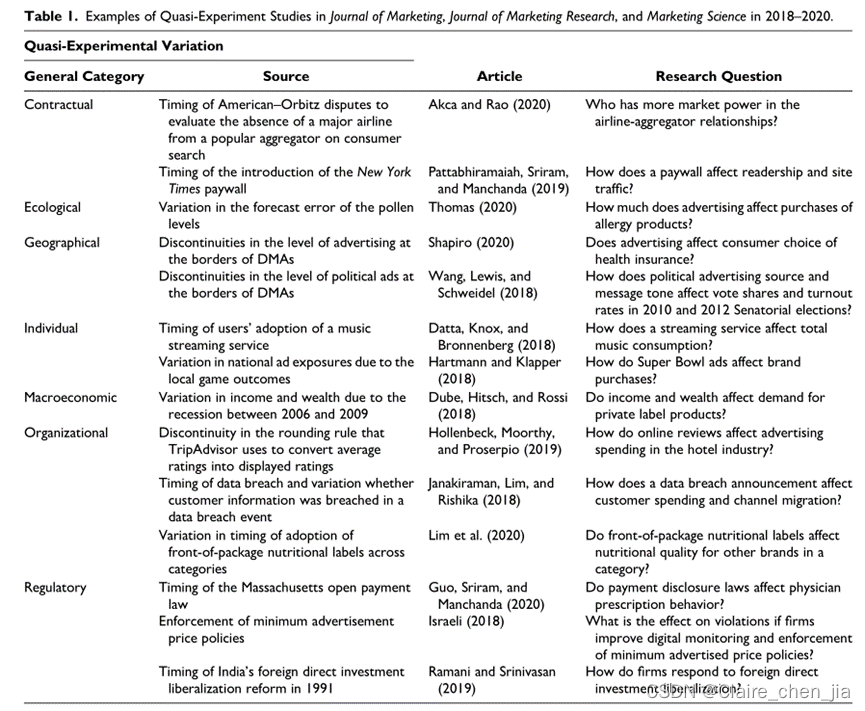
在这里插入图片描述

准实验回归

识别–>原始数据–>数据分析–>标准误–>稳健性分析–>机制分析
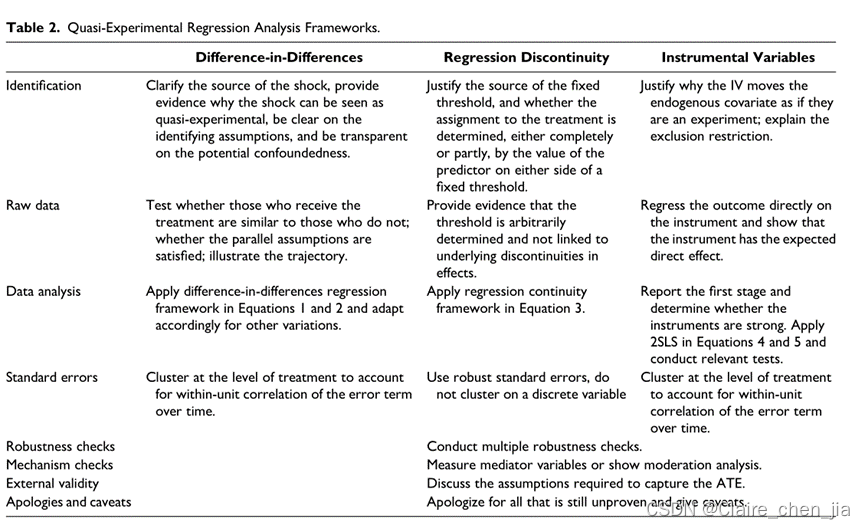
在这里插入图片描述

内生问题解决

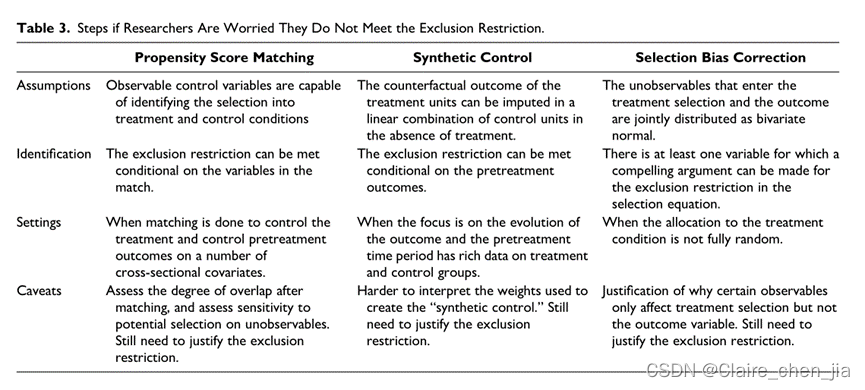
在这里插入图片描述

工具变量的注意事项

在这里插入图片描述
在这里插入图片描述

聚类的选择

在这里插入图片描述
在这里插入图片描述

相关文章：

论文笔记 | Conducting research in marketing with quasi-experiments

这篇论文是Journal of Marketing上的论文，讲了使用准实验来进行论文研究的一些事项。外生性识别的来源、几种准实验方法的注意点还有内生性的解决。 这篇论文对于准实验或者是平常论文的展开有一个非常友善的指导功能，可以阅读~ 摘要：本文旨…...

编程日记 2023/5/13 2:27:27

有关Android导览(Android Navigation component)

文章目录小结有关Android导览(Android Navigation component)碰到的问题参考小结 在使用Android导览(Android Navigation component)碰到很多问题。解决了一些问题，但是“Skipped xxx frames! The application may be doing too much work on its main thread”这样…...

编程日记 2023/5/13 2:27:25

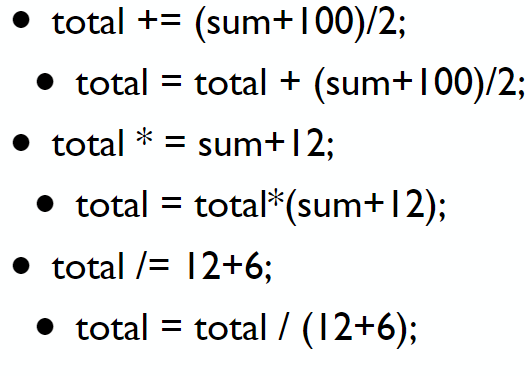
01 C语言计算

C语言计算 1、变量 用途：需要存放输入的数据 定义格式：数据类型 变量名（用于区分其他变量） 变量名格式：只能由字母/下划线/数字构成，首位不能是数字；且变量名不能是标识符 **变量赋值和初始…...

编程日记 2023/5/12 7:21:50

java单元测试简介（基于SpringBoot）

java单元测试简介（基于SpringBoot）mockitomock创建mock对象的另一种方式：Mockverifystubbing(存根)Spy（间谍）mock 静态方法mockito在springboot mock中的实战mockito 通常，在我们写单测时，会遇…...

编程日记 2023/5/14 5:14:30

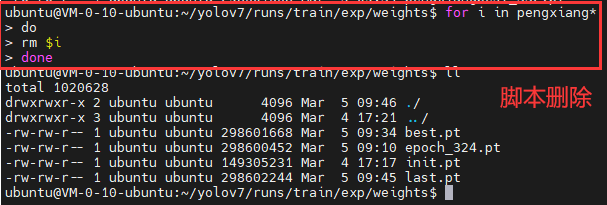
Linux常用命令操作

文件目录操作 查看文件列表 ls #输出列表信息 ls -l #输出详细列表信息 ls -a #输出隐藏文件 ls -la #输出包含的隐藏文件及详细信息 ll # ls-l的缩写rwx分别对应读取，写入，执行权限，前面有d代表是文件夹 创建文件 touch file.txt #创建…...

编程日记 2023/5/13 2:27:23

SpringCloud GateWay配置—TLS 和 SSL、Http超时配置

一、TLS 和 SSL网关可以按照通常的 Spring 服务器配置侦听 HTTPS 上的请求。 以下示例演示如何执行此操作：application.ymlserver:ssl:enabled: truekey-alias: scgkey-store-password: scg1234key-store: classpath:scg-keystore.p12key-store-type: PKCS12您可以将…...

编程日记 2023/5/13 2:27:21

python Django中的cookies和session会话保持技术

cookies和session都是为了保持会话状态而诞生的两个存储技术会话定义： 从打开浏览器访问一个网站，到关闭浏览器结束此次访问，称之为一次会话HTTP协议是无状态的，导致会话状态难以保持Cookies-定义 cookies是保存在客户端浏览器上的…...

编程日记 2023/5/13 2:27:18

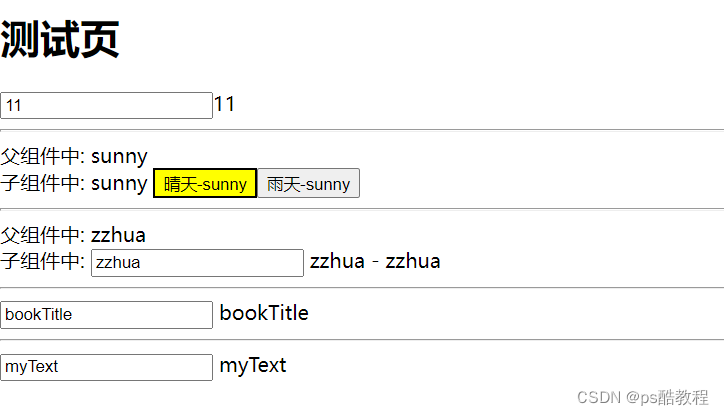
vue3的v-model指令

1. 普通input输入框双向绑定 <template><!-- 1. 普通input输入框双向绑定 --><!-- 其实等价于&#xff1a;<input :modelValue"title" update:modelValue"newTitle>titlenewTitle"/> --><input type"text" v-mod…...

编程日记 2023/5/13 2:27:16

Matlab小波去噪——基于wden函数的去噪分析

文章目录一、问题描述二、代码问题1&#xff1a;原始信号加6分贝高斯白噪声问题2&#xff1a;确定合适的小波基函数问题3&#xff1a;确定最合适的阈值计算估计方法问题4&#xff1a;确定合适的分解层数问题5&#xff1a;实际信号去噪问题6&#xff1a;对比三、演示视频最后一、…...

编程日记 2023/5/13 2:27:14

分布式对象存储——Apache Hadoop Ozone

前言 本文隶属于专栏《大数据技术体系》&#xff0c;该专栏为笔者原创&#xff0c;引用请注明来源&#xff0c;不足和错误之处请在评论区帮忙指出&#xff0c;谢谢&#xff01; 本专栏目录结构和参考文献请见大数据技术体系 1. 概述 Ozone是Apache Hadoop项目的子项目&#xf…...

编程日记 2023/5/13 2:27:10

Linux 和数据库笔记-03

今天主要内容数据库相关介绍数据库(软件)常见类型Navicat 工具基本使用常见的数据类型和约束(重点)SQL 语句的编写(表和数据)一. 数据库是什么?为什么学习数据库软件中产生的所有数据, 最终都要存储于数据库当中测试人员如果想要进行数据查询/数据校验, 就必须掌握对数据库的基…...

编程日记 2023/5/13 2:27:08

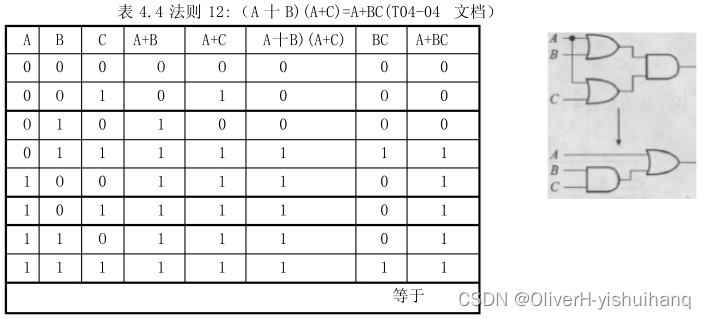
布尔定律---布尔代数的基本定律

一、单变量布尔定律 1、0-1定律 2、互补定律 3、重叠定律 4、还原定律 小结&#xff1a;或运算和与运算定律的差别在于&#xff1a;所有的“|”运算符换成“&”&#xff0c;运算结果为 0 换成 1。这就是对偶定律。它不仅是单逻辑变量的定律&#xff0c;而且对于所有布尔定…...

编程日记 2023/5/13 2:27:06

OSG三维渲染引擎编程学习之七十五：“第七章：OSG场景图形交互” 之 “7.6 多视图”

目录 第七章 OSG场景图形交互 7.6 多视图 7.6.1 多视图描述 7.6.2 多视图相机示例 第七章 OSG场景图形交互 作为一个成熟的三维渲染引擎，需...

编程日记 2023/5/13 2:27:03

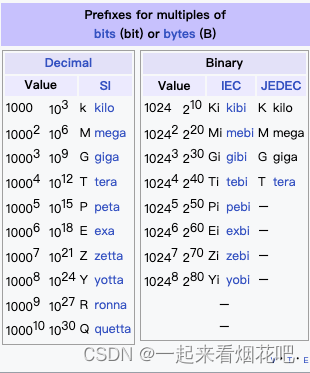
【计算机】单位制前缀的歧义-KB、kb、MB混用

引言 经常遇到容量、带宽的单位&#xff0c;MB&#xff0c;GB在进行单位换算时&#xff0c;总是傻傻分不清&#xff0c;查些资料浅记录一下。 公制&#xff08;metric system&#xff09; 又译米制&#xff0c;是一个国际化十进位量度系统。法国在1799年开始使用公制&#xf…...

编程日记 2023/5/13 2:27:01

nodejs调用浏览器打开URL链接

本文主要介绍的是node.js调用Chrome浏览器/默认浏览器打开链接地址的相关内容&#xff0c;分享出来供大家参考学习&#xff0c;下面来一起看看详细的介绍&#xff1a; 安装第三方插件open 通过open模块&#xff0c;可以在任何平台上打开某个浏览器网址。 通过NPM安装 npm i…...

编程日记 2023/5/13 2:26:59

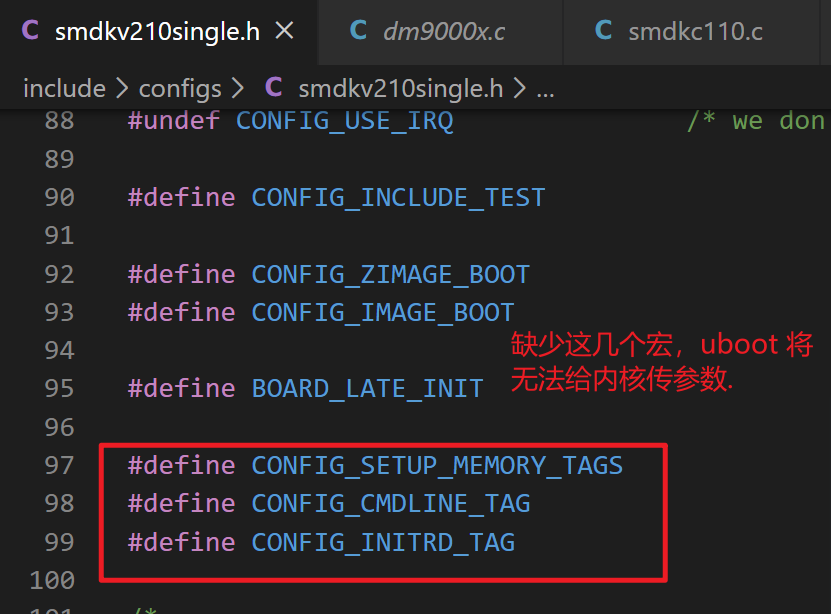
ARM uboot 的移植2-从三星官方 uboot 开始移植

一、inand 驱动问题的解决 1、先从现象出发定位问题 (1) 解决问题的第一步&#xff0c;是定位问题。所谓定位问题&#xff0c;就是找到源代码当中导致这个问题的那一句或者那几句代码。有时候解决这个问题需要修改的代码和直接导致这个问题的代码是不同的。我们这里说的定位问…...

编程日记 2023/5/13 2:26:57

js作用域和作用域链

1、局部作用域分为函数作用域和块作用域 1.1、函数作用域: 在函数内部声明的变量只能在函数内部被访问&#xff0c;外部无法直接访问。 总结 1.函数内部声明的变量&#xff0c;在函数外部无法被访问 2.函数的参数也是函数内部的局部变量 3.不同函数内部声明的变量无法互相访…...

编程日记 2023/5/13 2:26:53

C语言字符串

目录 一、字符串的引入和注意事项 1.1 字符串定义的几种方式&#xff1a; 1.2 定义字符串的方法一和方法二的区别&#xff1a; 1.3 字符串输出的几种方式&#xff1a; 1.3.1 循环下标法遍历输出字符串&#xff1a; 1.3.2 转义字符%s输出字符串&#xff1a; 1.3.3 使用puts函…...

编程日记 2023/5/13 2:26:51

Eureka注册中心快速入门

一、提供者与消费者**服务提供者&#xff1a;**一次业务中&#xff0c;被其他微服务调用的服务。&#xff08;提供接口给其他微服务&#xff09;**服务消费者&#xff1a;**一次业务中&#xff0c;调用其他微服务的服务。&#xff08;调用其它微服务提供的接口&#xff09;比如…...

编程日记 2023/5/13 2:26:49

xmu 离散数学 卢杨班作业详解【1-3章】

文章目录第一章 命题逻辑常用latex数学公式1.4.5679101113171923242627第二章 一阶逻辑1.2.3.6.9.10.12.13.一阶逻辑推理理论12.13.15.第三章 集合2478101213.第一章 命题逻辑 常用latex数学公式 符号代码∨\vee∨$\vee$∧\wedge∧$\wedge$→\rightarrow→$\rightarrow$⇒\Ri…...

编程日记 2023/5/13 2:26:46

谷歌浏览器插件

项目中有时候会用到插件 sync-cookie-extension1.0.0&#xff1a;开发环境同步测试 cookie 至 localhost&#xff0c;便于本地请求服务携带 cookie 参考地址&#xff1a;https://juejin.cn/post/7139354571712757767 里面有源码下载下来&#xff0c;加在到扩展即可使用FeHelp…...

编程新知 2025/8/16 3:55:30

springboot 百货中心供应链管理系统小程序

一、前言 随着我国经济迅速发展&#xff0c;人们对手机的需求越来越大&#xff0c;各种手机软件也都在被广泛应用&#xff0c;但是对于手机进行数据信息管理&#xff0c;对于手机的各种软件也是备受用户的喜爱&#xff0c;百货中心供应链管理系统被用户普遍使用&#xff0c;为方…...

编程新知 2026/2/8 20:41:49

树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频

使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源&#xff1a; http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

编程新知 2025/11/5 13:03:58

条件运算符

C中的三目运算符&#xff08;也称条件运算符&#xff0c;英文&#xff1a;ternary operator&#xff09;是一种简洁的条件选择语句&#xff0c;语法如下&#xff1a; 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true&#xff0c;则整个表达式的结果为“表达式1”…...

编程新知 2025/12/6 22:50:48

12.找到字符串中所有字母异位词

&#x1f9e0; 题目解析 题目描述&#xff1a; 给定两个字符串 s 和 p&#xff0c;找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义&#xff1a; 若两个字符串包含的字符种类和出现次数完全相同&#xff0c;顺序无所谓&#xff0c;则互为…...

编程新知 2026/1/31 12:52:29

【HarmonyOS 5 开发速记】如何获取用户信息（头像/昵称/手机号）

1.获取 authorizationCode&#xff1a; 2.利用 authorizationCode 获取 accessToken&#xff1a;文档中心 3.获取手机&#xff1a;文档中心 4.获取昵称头像&#xff1a;文档中心 首先创建 request 若要获取手机号&#xff0c;scope必填 phone&#xff0c;permissions 必填 …...

编程新知 2025/9/17 2:39:21

Mysql8 忘记密码重置，以及问题解决

1.使用免密登录 找到配置MySQL文件&#xff0c;我的文件路径是/etc/mysql/my.cnf&#xff0c;有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

编程新知 2026/1/9 8:59:09

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师（题目+回答）

安全领域各种资源&#xff0c;学习文档&#xff0c;以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具&#xff0c;欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

编程新知 2026/1/27 2:41:27

Oracle11g安装包

Oracle 11g安装包 适用于windows系统&#xff0c;64位 下载路径 oracle 11g 安装包...

编程新知 2025/9/13 16:14:04

《信号与系统》第 6 章 信号与系统的时域和频域特性

目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...

编程新知 2026/2/5 4:45:50