数据结构与算法:堆排序和TOP-K问题
朋友们大家好,本节内容来到堆的应用:堆排序和topk问题
堆排序
- 1.堆排序的实现
- 1.1排序
- 2.TOP-K问题
- 3.向上调整建堆与向下调整建堆
- 3.1对比两种方法的时间复杂度
我们在c语言中已经见到过几种排序,冒泡排序,快速排序(qsort)
冒泡排序的时间复杂度为O(N2),空间复杂度为O(1);qsort排序的时间复杂度为
O(nlogn),空间复杂度为O(logn),而今天所讲到的堆排序在时间与空间复杂度上相比于前两种均有优势
堆排序可以在原数组上进行,其空间复杂度为O(1);
堆排序提供了稳定的 (O(nlogn)) 时间复杂度
接下来我们进行讲解
首先我们来看这组代码:
int main()
{int a[] = { 6,3,5,7,11,4,9,13,1,8,15 };Heap hp;HeapInit(&hp);for (int i = 0; i < sizeof(a) / sizeof(int); i++){HeapPush(&hp, a[i]);}while (!HeapEmpty(&hp)){printf("%d ", HeapTop(&hp));HeapPop(&hp);}printf("\n");return 0;}
上节课我们知道,hp这个堆里面,a[i]并不一定是有序的
这里我们每次打印首元素,即最小元素,再删除掉,下一次获得到的堆顶元素仍为最小的,所以打印出来结果为有序的。但这个并不是堆排序,他只是每次获取堆顶最小元素
堆排序是直接在数组上实现的
1.堆排序的实现
堆排序的实现可以分为两部分:构建最大堆(或最小堆)和执行排序过程
首先我们来看建堆过程:
在上述代码中,我们是通过HeapPush(&hp, a[i]);来实现堆的插入,推其本质,是每次插入元素后进行向上调整,我们构建一个堆排序函数,其参数为传入的数组,和数组的元素个数:
void HeapSort(HPDataType* a, int n);
首先建堆,这里我们用向上调整建堆,在文章末尾会给大家引入向下调整建堆
for (int i = 1; i < n; i++)
{Ajustup(a, i);
}
从第二个元素开始,每次向上调整,完成堆的构建
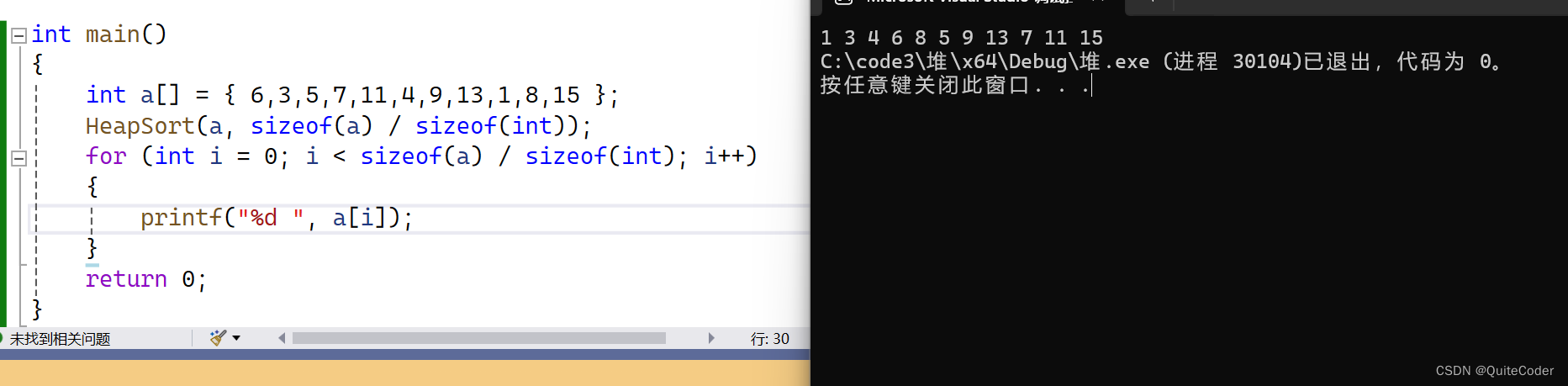
建好之后我们则需要排序
1.1排序
思考一下,如果我们想要进行升序排序,需要建立大堆还是小堆呢?
在上述示例中,如果我们想进行升序,该怎么操作???
这里,如果我们想要升序排序,则需要建立大堆
小堆如果我们想要升序,堆顶元素在对应位置,剩余元素重新建立小堆,则时间复杂度大大增加
上述示例中,我们建了一个小堆,可以将Ajustup父节点与子节点大小关系改变来建立为大堆:
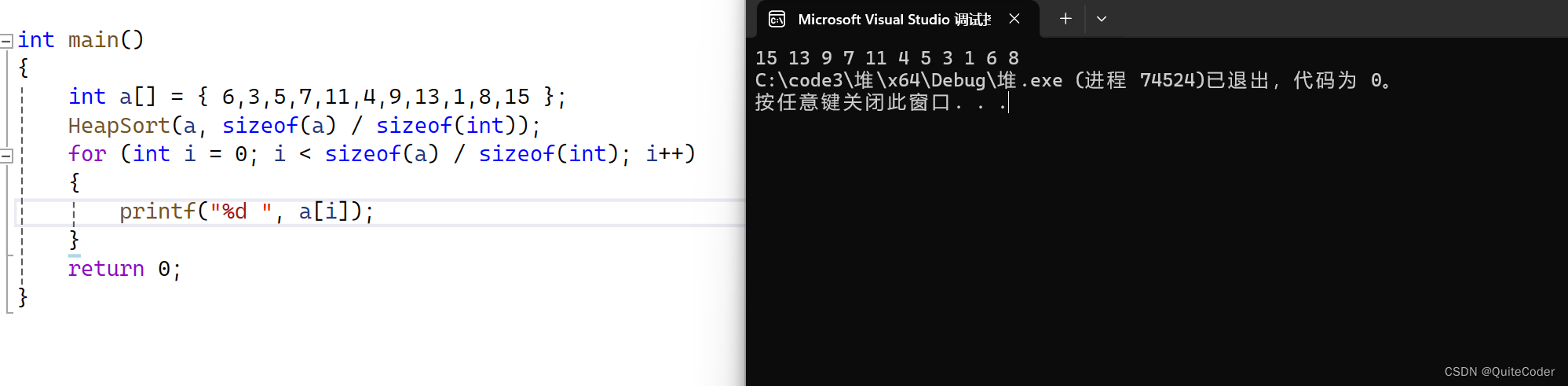
那思考一下,建立了大堆,我们如何实现升序呢?
这里我们就需要与删除堆顶元素相同的思路
-
排序过程
在大堆构建完成后,数组的根节点(即数组的第一个元素)是当前堆中的最大元素。通过将它与堆的最后一个元素交换,然后减少堆的大小(实际上是忽略数组的末尾元素),可以确保最大元素位于数组的正确位置上。 -
调整堆
交换根节点和最后一个节点之后,新的根节点可能破坏了大堆的性质,因此需要进行调整。调整的方法是将新的根节点“下沉”,直到恢复大堆的性质。 -
重复过程
重复对堆顶元素进行移除并调整堆的过程,直到堆的大小减少到1。在每一次重复过程中,都会将当前的最大元素放置到它在数组中的最终位置上。
所以我们代码实现就两步:
- 交换首尾元素
- 向下调整
void HeapSort(HPDataType* a, int n)
{//建堆for (int i = 1; i < n; i++){Ajustup(a, i);}while (n>1){Swap(&a[0], &a[n - 1]);n--;Ajustdown(a, n, 0);}
}
我们进行代码测试
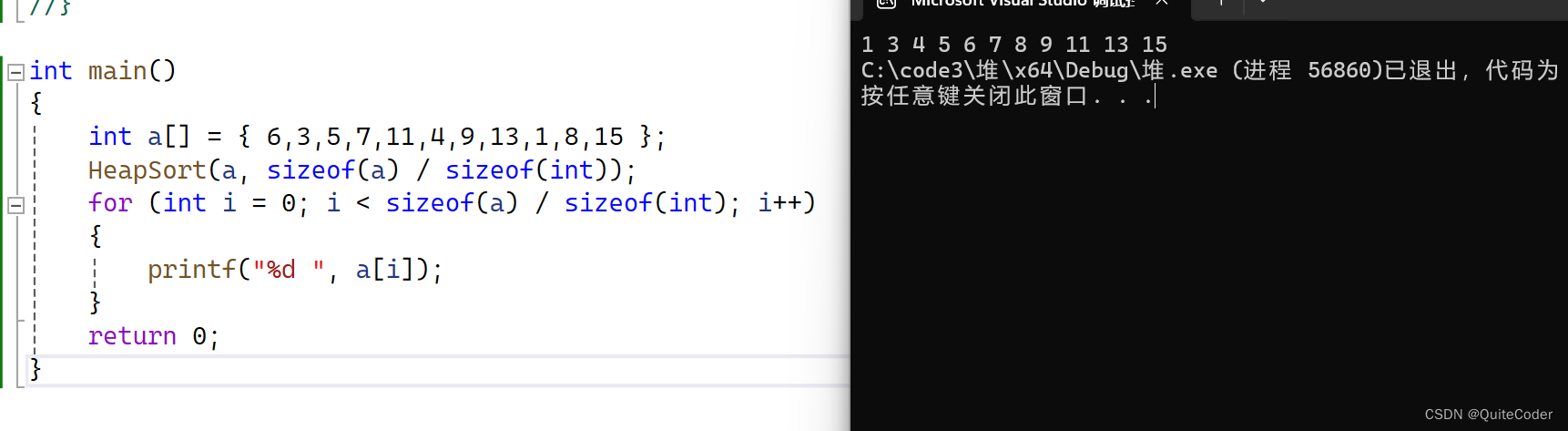
所以,堆这里可以促进我们快速选数,它的本质是选择排序
2.TOP-K问题
TOP-K问题指的是从一个大规模的数据集中找出“最重要”或“最优”的K个元素的问题,对于Top-K问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决
思路如下:
- 用数据集合中前K个元素来建堆
- 前k个最大的元素,则建小堆
- 前k个最小的元素,则建大堆
- 用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素
基于已经提供的堆操作函数,我们可以实现一个特定的PrintTopK函数,其目的是从数组a中找到最大的k个元素。
实现这一目标的思路是:
- 首先,使用数组a中的前k个元素建立一个最小堆。
- 然后,遍历剩余的n-k个元素。对于每个元素,如果它大于堆顶元素,则用它替换堆顶元素,然后对堆顶元素进行向下调整以维护最小堆的性质。
- 遍历完成后,堆中的k个元素即为整个数组中最大的k个元素。
void PrintTopK(int* a, int n, int k)
{Heap php;HeapInit(&php);for (int i = 0; i < k; ++i) {HeapPush(&php, a[i]);}for (int i = k; i < n; ++i) {if (a[i] > HeapTop(&php)) { // 如果当前元素比堆顶大HeapPop(&php); // 移除堆顶HeapPush(&php, a[i]); // 将当前元素加入堆中}}// 打印堆中的元素,即TOP K元素for (int i = 0; i < k; ++i) {printf("%d ", php.a[i]);}printf("\n");HeapDestroy(&php);
}- 用a中前k个元素建立堆
- 将剩余n-k个元素与堆顶比较,替换并调整
测试代码:
3.向上调整建堆与向下调整建堆
对于数组a,进行向上调整建堆:
for (int i = 1; i < n; i++)
{Ajustup(a, i);
}
要通过向下调整的方式建立堆,我们通常是从最后一个非叶子节点开始,逐层向上进行调整,这能保证每个子树都满足堆的性质
for (int i = n/2 - 1; i >= 0; i--) {AdjustDown(a, n, i);}
3.1对比两种方法的时间复杂度
向下调整建堆:
这个方法从最后一个非叶子节点开始,逆序对数组中的元素执行向下调整的操作。每个节点需要执行的向下调整操作取决于其高度,而数组中大约一半的节点是叶子节点,它们不需要被向下调整。对于剩下的节点,只有很少的节点需要移动到树的较低层次。具体地说,树的每一层上的节点数量减半,而向下移动的最大深度从0开始线性增加。
for (int i = n/2 - 1; i >= 0; i--) {AdjustDown(a, n, i);
}
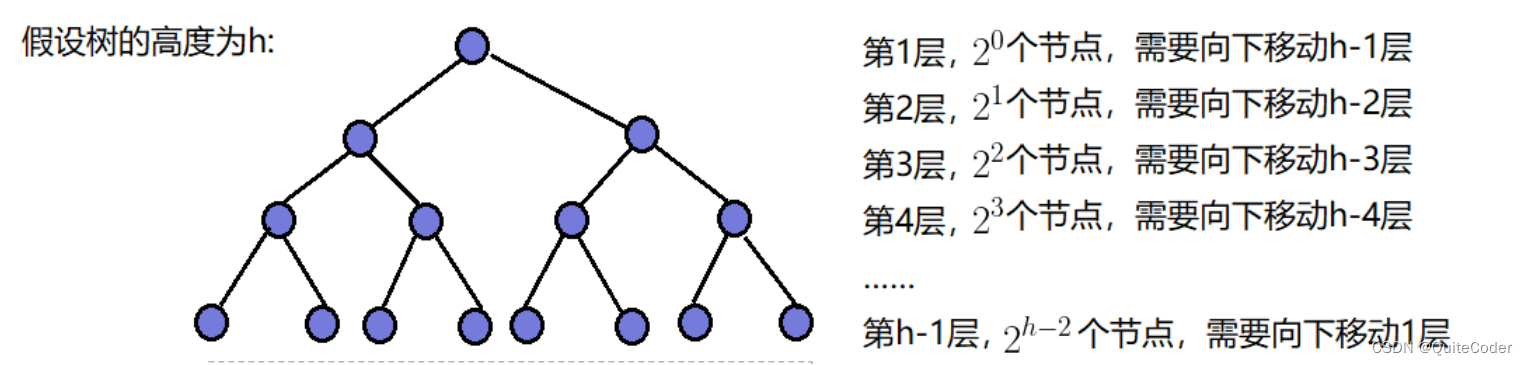
设向下调整的累计次数为T(h).
- 倒数第二层调整次数:2h-2*1
- 倒数第三层调整次数:2h-3*2
- ……
- 第一层调整次数:20*(h-1);
对其进行累加和:
为等差×等比求和,通过错位相减则可求出结果:
T(h)=2^h-1-h;
h=log (n+1);
T(n)=n-log(n+1)
导致最大影响的项为n
所以向下调整的时间复杂度为O(N)
向上调整建堆
从第二层开始向上调整:
- 第二层调整次数:21*1
- 第三层调整次数:22*2;
- 倒数第二层:2h-2*(h-2);
- 倒数第一层:2h-1*(h-1);
向上调整建堆
对于一个节点来说,向上调整可能需要比较和移动直到它的根节点,这在最坏的情况下是树的高度,对于一个完全二叉树来说,树的高度是 O ( log n ) O(\log n) O(logn)。对于代码段:
for (int i = 1; i < n; i++) {AdjustUp(a, i);
}
这个方法从第二个元素开始,逐一对数组中的元素执行向上调整的操作。对于数组中的第i个元素,最坏情况下向上调整操作需要沿着一条从叶节点到根节点的路径移动,路径的长度大约等于树的高度 h h h,即 O ( log i ) O(\log i) O(logi)。因此,对于所有元素的总时间复杂度为:
T ( n ) = ∑ i = 1 n O ( log i ) = O ( log n ! ) = O ( n log n ) T(n) = \sum_{i=1}^{n} O(\log i) = O(\log n!) = O(n \log n) T(n)=i=1∑nO(logi)=O(logn!)=O(nlogn)
使用斯特灵公式( n ! ≈ 2 π n ( n e ) n n! \approx \sqrt{2\pi n}(\frac{n}{e})^n n!≈2πn(en)n),可以推导出 O ( log n ! ) O(\log n!) O(logn!) 的大致等于 O ( n log n ) O(n \log n) O(nlogn),所以向上调整建堆的时间复杂度大约为 O ( n log n ) O(n \log n) O(nlogn)。
向上调整建堆的时间复杂度是 O ( n log n ) O(n \log n) O(nlogn),而向下调整建堆的时间复杂度是 O ( n ) O(n) O(n)。因此,对于从零开始构建堆的场景,通常更倾向于使用向下调整的方法,因为它更加高效。
本节内容到此结束!感谢大家支持!
相关文章:

数据结构与算法:堆排序和TOP-K问题
朋友们大家好,本节内容来到堆的应用:堆排序和topk问题 堆排序 1.堆排序的实现1.1排序 2.TOP-K问题3.向上调整建堆与向下调整建堆3.1对比两种方法的时间复杂度 我们在c语言中已经见到过几种排序,冒泡排序,快速排序(qsor…...

【NR 定位】3GPP NR Positioning 5G定位标准解读(三)
目录 前言 5 NG-RAN UE定位架构 5.1 架构 5.2 UE定位操作 5.3 NG-RAN定位操作 5.3.1 通用NG-RAN定位操作 5.3.2 OTDOA定位支持 5.3.3 广播辅助信息支持 5.3.4 NR RAT相关定位支持 5.4 NG-RAN中与UE定位相关的元素功能描述 5.4.1 用户设备(UE) …...
文件操作与IO(3) 文件内容的读写——数据流
目录 一、流的概念 二、字节流代码演示 1、InputStream read方法 第一个没有参数的版本: 第二个带有byte数组的版本: 第三个版本 搭配Scanner的使用 2、OutputStream write方法 第一个版本: 第二个写入整个数组版本: …...
《PyTorch深度学习实践》第十一讲卷积神经网络进阶
一、 1、卷积核超参数选择困难,自动找到卷积的最佳组合。 2、1x1卷积核,不同通道的信息融合。使用1x1卷积核虽然参数量增加了,但是能够显著的降低计算量(operations) 3、Inception Moudel由4个分支组成,要分清哪些是在Init里定义…...

Ansible的playbook的编写和解析
目录 什么是playbook Ansible 的脚本 --- playbook 剧本 实例部署(使用playbook安装启动httpd服务) 1.编写一个.yaml文件 在主机下载安装http,将配置文件复制到opt目录下 运行playbook 在192.168.17.77主机上查看httpd服务是否成功开启…...

[环境配置]ssh连接报错“kex_exchange_identification: read: Connection reset by peer”
已经被VScode ssh毒死好几次了,都是执行命令意外中断,然后又VSCode里连不上、本机Terminal也连不上了。。。 重启远程服务器,VSCode可以连上了, 系统ssh还是不行,报错“kex_exchange_identification: read: Connecti…...
Mybatis-Plus——04,自动填充时间(新注解)
自动填充(新注解) 一、数据库添加两个字段二、实体类字段属性上增加注解三、编写填充器四、查看结果4.1 插入结果4.2 修改结果 五、同步修改5.1实体类属性改成 INSERT_UPDATE5.2 在填充器的方法这里加上 updateTime5.3 查看结果————————创作不易…...

【动态规划入门】最长上升子序列
每日一道算法题之最长上升子序列 一、题目描述二、思路三、C代码 一、题目描述 题目来源:LeetCode 给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。 输入格式 第一行包含整数 N。 第二行包含 N个整数,表示完整序列。 输出格式 输出一个整数…...
LabVIEW眼结膜微血管采集管理系统
LabVIEW眼结膜微血管采集管理系统 开发一套基于LabVIEW的全自动眼结膜微血管采集管理系统,以提高眼结膜微血管临床研究的效率。系统集成了自动化图像采集、图像质量优化和规范化数据管理等功能,有效缩短了图像采集时间,提高了图像质量&#…...
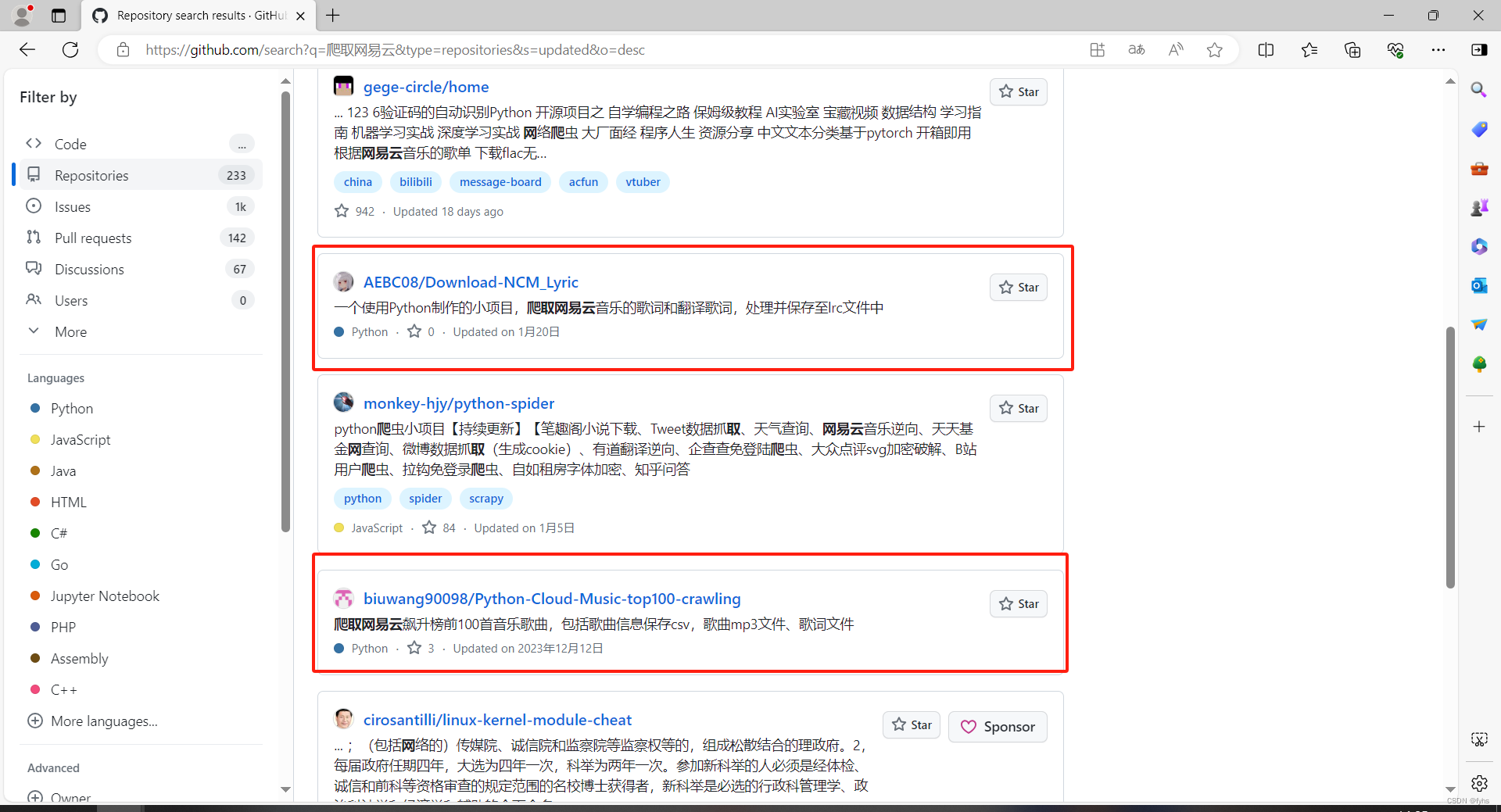
通过GitHub探索Python爬虫技术
1.检索爬取内容案例。 2.找到最近更新的。(最新一般都可以直接运行) 3.选择适合自己的项目,目前测试下面画红圈的是可行的。 4.方便大家查看就把代码粘贴出来了。 #图中画圈一代码 import requests import os import rewhile True:music_id input("请输入歌曲…...
【Python】-----基础知识
注释 定义:让计算机跳过这个代码执行用三个单引号/双引号都表示注释信息,在Python中单引号与双引号没有区别,但必须是成对出现 输出与输入 程序是有开始,有结束的,程序运行规则:从上而下,由内…...
:点云处理相关开源算法库、软件、工具)
如何学习、上手点云算法(二):点云处理相关开源算法库、软件、工具
写在前面 本文内容 一些用于点云处理的开源算法库、软件介绍,主要包含: CloudCompare, MeshLab, PCL, Open3D, VTK, CGAL等 不定时更新 平台/环境 Windows10, Ubuntu1804, CMake, Open3D, PCL 转载请注明出处: https://blog.csdn.net/qq_41…...

为什么会对猫毛过敏?如何缓解?浮毛克星—宠物空气净化器推荐
猫咪过敏通常是因为它们身上的Fel d1蛋白质导致的,这些蛋白质附着在猫咪的皮屑上。猫咪舔毛的过程会带出这些蛋白质,一旦接触就可能引发过敏症状,比如打喷嚏等。因此,减少空气中的浮毛数量有助于减轻过敏现象。猫用空气净化器可以…...

Linux学习-etcdctl安装
etcdctl3.5下载链接 1. 先通过上面链接下载gz包2. 解压 [rootk8s-master ~]# tar xf etcd-v3.5.11-linux-amd64.tar.gz [rootk8s-master etcd-v3.5.11-linux-amd64]# ls Documentation etcd etcdctl etcdutl README-etcdctl.md README-etcdutl.md README.md READMEv2-e…...

Qt应用软件【文件篇】读写文件技巧
文章目录 简介按照偏移读文件按照偏移写文件Qt按行写文件Qt按行读文件注意事项指定文件编码格式UTF8转GBK简介 Qt提供了丰富的API来处理文件读写操作,使得读写文件变得简单。 按照偏移读文件 QFile file("example.txt"); if (file.open(QIODevice::ReadOnly)) {q…...

GO常量指针
Go语言中的常量使用关键字const定义,用于存储不会改变的数据,常量是在编译时被创建的,即使定义在函数内部也是如此,并且只能是布尔型、数字型(整数型、浮点型和复数)和字符串型。 由于编译时的限制&#x…...
微服务间通信重构与服务治理笔记
父工程 依赖版本管理,但实际不引入依赖 pom.xml <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation&…...
unity 场景烘焙中植物叶片(单面网络)出现的白面
Unity版本 2021.3.3 平台 Windows 在场景烘焙中烘焙植物的模型的时候发现植物的叶面一面是合理的,背面是全白的,在材质球上勾选了双面烘焙,情况如下 这个问题可能是由于植物叶片的单面网格导致的。在场景烘焙中,单面网格只会在一…...

网工内推 | 国企运维,年薪最高30W,RHCE认证优先
01 上海华力微电子有限公司 招聘岗位:系统运维资深/主任工程师 职责描述: 1、负责IT基础设施(包括服务器、存储、中间件等系统基础技术平台)的设计建设和日常运维管理; 2、负责生产、开发和测试环境的技术支持&#x…...

WordPress排除调用某个分类下的文章
wordpress在调用分类下文章时,有时需要排除调用某个分类的文章,下面的这段代码,就可以轻松实现不调用特定ID的分类内容。 <?phpquery_posts("showposts10&cat-1"); //cat-1为排除ID为1的分类下文章while(have_posts()) : …...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...
