【笔记】【电子科大 离散数学】 3.谓词逻辑
谓词引入
因为含变量的语句(例如x > 3)不是命题,无法进行逻辑推理。
为了研究简单命题句子内部的逻辑关系,我们需要对简单命题进行分解,利用个体词,谓词和量词来描述它们,并研究个体与总体的内在联系和数量关系,这就是谓词逻辑或者一阶逻辑
在原子命题中,可以独立存在的客体(句子中的主语、宾语),称为个体词。而用以刻划客体的性质或者客体之间的关系即是谓词
个体词的定义
个体词可分为两种,个体常量和个体变量,均在个体域内取值。
- 表示具体或者特定的个体词称为个体常量。一般用带或不带下标的小写英文字母 a , b , c , . . . a 1 , b 1 , c 1 . . . a, b, c,... a_1, b_1, c_1... a,b,c,...a1,b1,c1...来表示。
- 表示抽象或者泛指的个体词称为个体变量。一般用带或不带下标的小写英文字母 x , y , z , x 1 , . . . y 1 , z 1 . . . x, y, z, x_1,... y_1, z_1 ... x,y,z,x1,...y1,z1...来表示。
- 个体词的取值范围称为个体域(或者论域),常用D表示;
- 宇宙间的所有个体域聚集在一起所构成的个体域成为全总个体域。若无特别说明均使用全总个体域。
谓词的定义
设 D D D为非空的个体域,定义在 D n D^n Dn(表示 n n n个个体都在个体域 D D D上取值)上取值于 0 , 1 {0, 1} 0,1上的 n n n元函数,称为 n n n元命题函数或 n n n元谓词,记为 P ( x 1 , x 2 , . . . x n ) P(x_1, x_2, ... x_n) P(x1,x2,...xn)。其中,个体变量 x 1 , x 2 , . . . x n ∈ D x_1, x_2, ... x_n \in D x1,x2,...xn∈D。
- 表示具体性质或关系的谓词称为谓词常量。
- 表示抽象或者泛指的谓词称为谓词变量。
例子:

复合命题的谓词符号化

量词引入
谓词符号化
谓词公式
自由变元和约束变元
公式解释和分类
公式等价
前束范式
推理形式和推理规则
谓词综合推理
相关文章:

【笔记】【电子科大 离散数学】 3.谓词逻辑
谓词引入 因为含变量的语句(例如x > 3)不是命题,无法进行逻辑推理。 为了研究简单命题句子内部的逻辑关系,我们需要对简单命题进行分解,利用个体词,谓词和量词来描述它们,并研究个体与总体…...

倍增算法C++
倍增 倍增算法是一种优化算法,通常用于某些需要高效计算指数幂的场景。它基于分治的思想,通过反复求平方来实现快速计算指数幂的目的。在实际应用中,倍增算法经常用于解决最近公共祖先问题、二分查找等。 1、快速幂详解 ksm核心代码 倍增就是…...

uniapp制作--进步器的选择
介绍: 进步器的选择,一般用于商城购物选择物品数量的场景 注意:该输入框只能输入大于或等于0的整数 效果展示: 代码展示: 以下是一个简单的购物车页面示例,包括选择商品和显示数量的功能: 在这个示例中…...

前端高频面试--查缺补漏篇
什么是进程和线程,有什么区别 进程:进程是程序的一次执行过程,是动态的过程,有自身产生、存在、消亡的过程。 线程:线程由进程创建,是进程的一个实体。一个进程可以拥有多个线程。 举个例子:…...

【计算机学习】-- 网页视频加速
系列文章目录 文章目录 系列文章目录前言一、开发者选项二、定义和用法1.基础语法:2.什么是uncaught TypeError:Cannot read properties of null? 二、开发者工具面板:1.Elements面板:2.Console面板: 总结 前言 一、开发者选项 …...

系统运维-Linux配置C、C++、Go语言编译环境
C yum install gcc -y #安装gcc编译器 gcc --version #验证环境gcc (GCC) 11.3.1 20221121 (Red Hat 11.3.1-4) Copyright (C) 2021 Free Software Foundation, Inc. This is free software; see the source for copying conditions. There is NO warranty; not even f…...
【设计模式】(二)设计模式六大设计原则
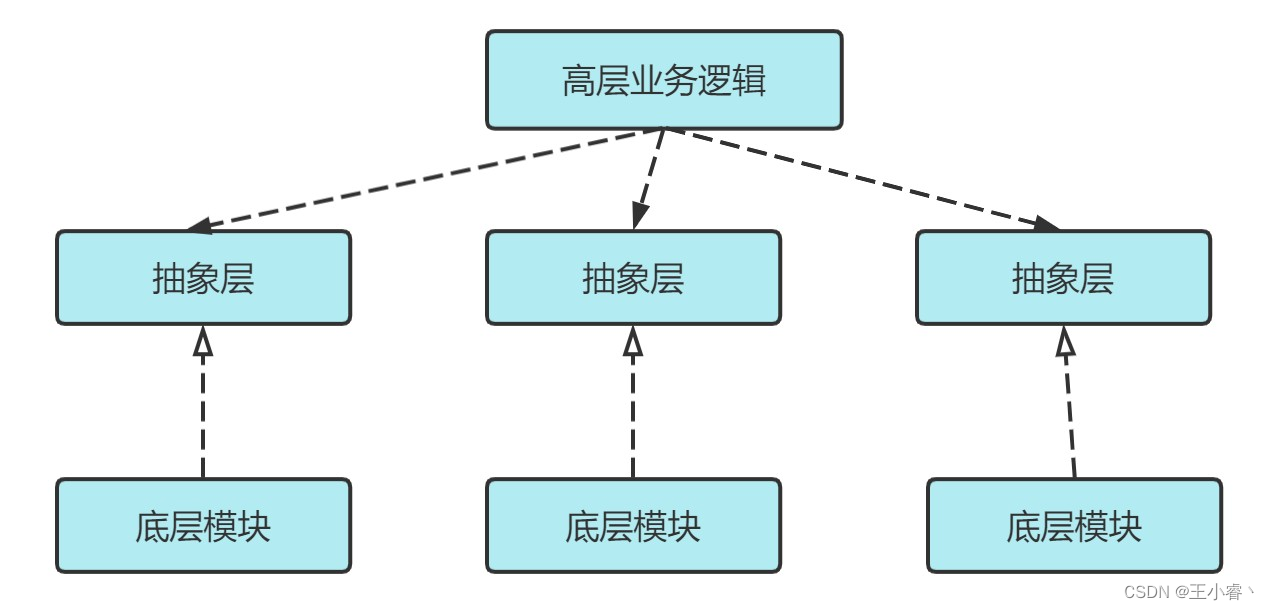
一、 设计原则概述 设计模式中主要有六大设计原则,简称为SOLID ,是由于各个原则的首字母简称合并的来(两个L算一个,solid 稳定的),六大设计原则分别如下: 1、单一职责原则(Single Responsibitity Principle&#…...

go-zero官网
go-zero 是一个集成了各种工程实践的 web 和 rpc 框架。通过弹性设计保障了大并发服务端的稳定性,经受了充分的实战检验。 go-zero官网:go-zero 缩短从需求到上线的距离...
)
Redis的应用场景以及常见问题(持续更新)
一、使用场景 1,在大型的秒杀库存扣减,app首页流量高峰,很容易将传统的关系型数据库(mysql,oracle等)给压垮 2,还有很多没必要持久化的数据,比如说短信验证码,点赞数等 3,…...

前端添加压缩包内文件名称校验
1. tar包内文件名称校验 1. 读取tar包内所有的文件名称 export class TarReader {fileInfo: any[]buffer: string | ArrayBufferconstructor() {this.fileInfo []}readFile(file) {return new Promise(resolve > {const reader new FileReader()reader.onload event &g…...
redis02 安装
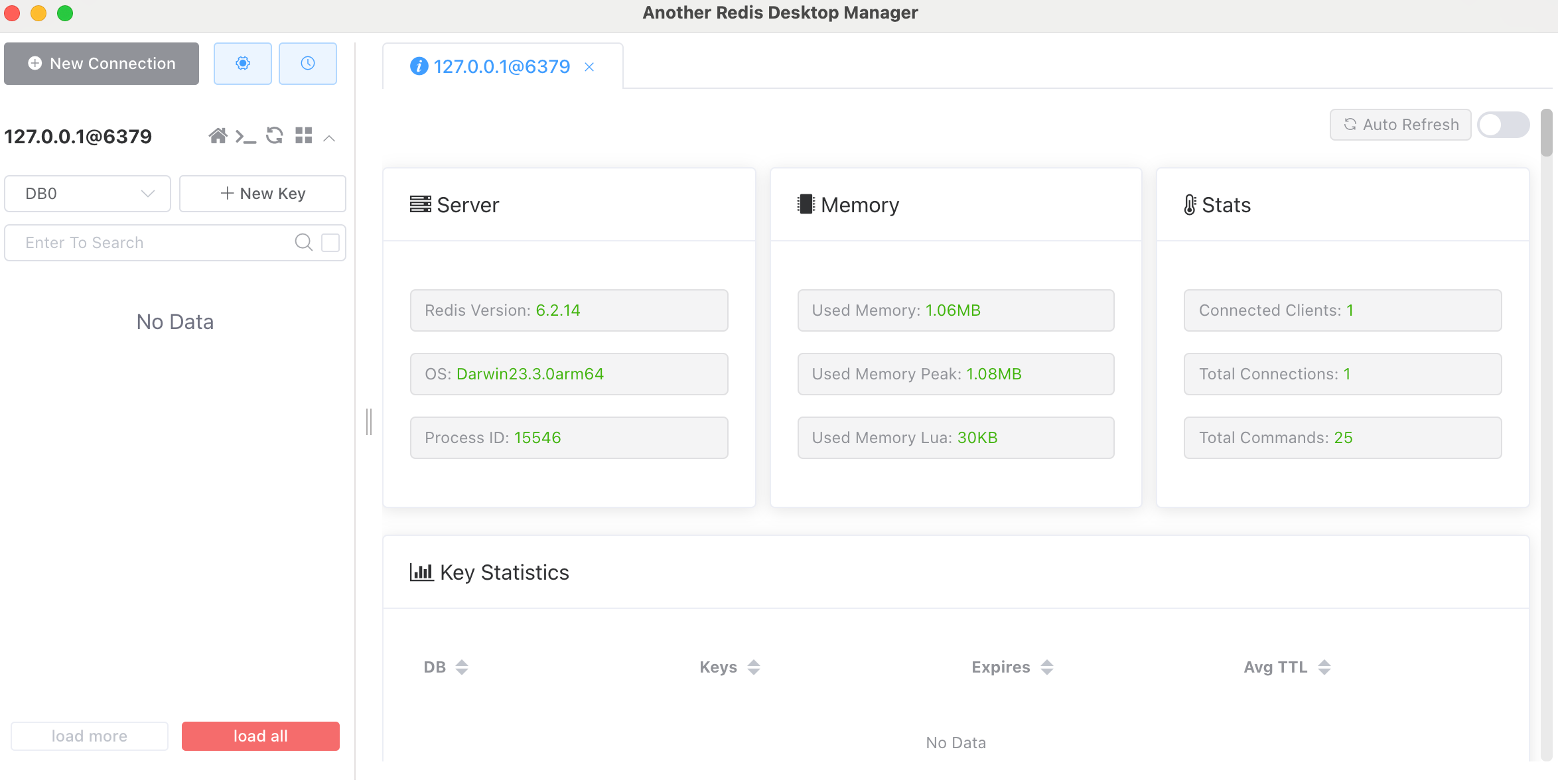
官网下载 传送门https://redis.io/download/#redis-downloads 安装Redis mac m1安装 下载你需要版本的软件包放到指定的目录下进行解压 cd 到解压好的redis目录 运行下面的命令进行编译测试 sudo make test 中途可能会提示你安装make工具,按提示安装即可&…...
)
#QT(QT时钟)
1.IDE:QTCreator 2.实验 3.记录 qtime(qt的时间类) qtimer(qt的定时类) 4.代码 widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QTime> // #include <QTimer&g…...

T-RAG:结合实体检测的增强检索生成模型
内容摘要: T-RAG是一种新的大型语言模型(LLM)应用框架,在保证数据隐私的同时,提高了对私有企业文档的问答系统性能。T-RAG通过结合已有的增强检索生成(RAG)框架、自定义的开源语言模型以及一个实…...

u-boot: NAND 驱动简介
文章目录 1. 前言2. NAND 初始化3. 访问 NAND 设备3.1 查看 NAND 设备信息3.1.1 查看 NAND 设备基本信息3.1.2 查看 NAND 设备 MTD 分区3.1.3 查看 NAND 设备坏块 3.2 NAND 擦除操作3.3 NAND 写操作3.4 NAND 读操作3.5 其它 NAND 操作 1. 前言 限于作者能力水平,本…...

史上最全的大数据开发八股文【自己的吐血总结】
自我介绍 我本硕都是双非计算机专业,从研一下开始学习大数据开发的相关知识,从找实习到秋招,我投递过100公司,拿到过10的offer,包括滴滴、字节、蚂蚁、携程、蔚来、去哪儿等大厂(岗位都是大数据开发&#…...
数据库学习案例20240304-mysql数据库案例总结(碎片,统计信息)
1 表中的碎片 在InnoDB中删除行的时候,这些行只是被标记为“已删除”,而不是真正从物理存储上进行了删除,因而存储空间也没有真正被释放回收。InnoDB的Purge线程会异步地来清理这些没用的索引键和行。但是依然没有把这些释放出来的空间还给操…...

【小白友好】LeetCode 删除并获得点数
基础题 打家劫舍https://leetcode.cn/problems/house-robber/ 小白解法 删除nums[i]就会使得所有nums[i]-1和nums[i]1的值都消失,手写了几个,发现找来找去不方便,还不如先排个序,然后这样nums[i]-1和nums[i]和nums[i]1就能靠在…...

c#委托、lambda、事件
Lambda Lambda表达式是一种匿名函数,Lambda表达式通常以箭头“>”分隔左侧的输入和右侧的输出。 (parameter_list) > { statement_block } parameter_list 是由一个或多个参数组成的逗号分隔列表,每个参数都包括类型和名称,可以为空。…...

每日一练——9×9乘法表
#include<stdio.h>int main() {int i 0; //乘数定义for (i 1; i < 9; i) //循环1到9 {int j 0;//被乘数定义for (j 1; j < i; j) //循环被乘数1到9{printf("%d*%d%2d ", i, j, i * j); 乘法}printf("\n"); 换行} return 0; }...

大白话解析LevelDB:ShardedLRUCache
文章目录 Cache 接口定义ShardedLRUCache 的实现ShardedLRUCache 的构造函数ShardedLRUCache::Insert(const Slice& key, void* value, size_t charge, void (\*deleter)(const Slice& key, void* value))ShardedLRUCache::Lookup(const Slice& key)ShardedLRUCach…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...

对象回调初步研究
_OBJECT_TYPE结构分析 在介绍什么是对象回调前,首先要熟悉下结构 以我们上篇线程回调介绍过的导出的PsProcessType 结构为例,用_OBJECT_TYPE这个结构来解析它,0x80处就是今天要介绍的回调链表,但是先不着急,先把目光…...
