堆和二叉树的动态实现(C语言实现)

✅✅✅✅✅✅✅✅✅✅✅✅✅✅✅✅
✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨
🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿
🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟
🌟🌟 追风赶月莫停留 🌟🌟
🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀
🌟🌟 平芜尽处是春山🌟🌟
🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟
🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿
✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨
✅✅✅✅✅✅✅✅✅✅✅✅✅✅✅✅
🍋堆和队二叉树
- 🍑二叉树
- 🍍二叉树的含义
- 🍍二叉树的结构
- 🍍二叉树的存储结构
- 🍑堆
- 🍍堆的含义
- 🍍堆的结构
- 🍍堆的实现
- 🍌补充条件
- 🍌堆的初始化
- 🍌堆的销毁
- 🍌堆的插入
- 🍌 堆的删除
- 🍌取堆顶的数据
- 🍌堆的数据个数
- 🍌堆的判空
- 🍌堆的整体代码实现
🍑二叉树
🍍二叉树的含义
二叉树是一种树形结构,其特点是每个节点最多有两个子树。
二叉树是一种有序树,这意味着它的子树按照一定的顺序排列,通常左子树出现在右子树之前。二叉树的递归定义可以描述为:二叉树可以是空的,也可以由一个根节点和两个互不相交的子树组成,这两个子树分别称为左子树和右子树。左子树和右子树自身也构成二叉树。
🍍二叉树的结构

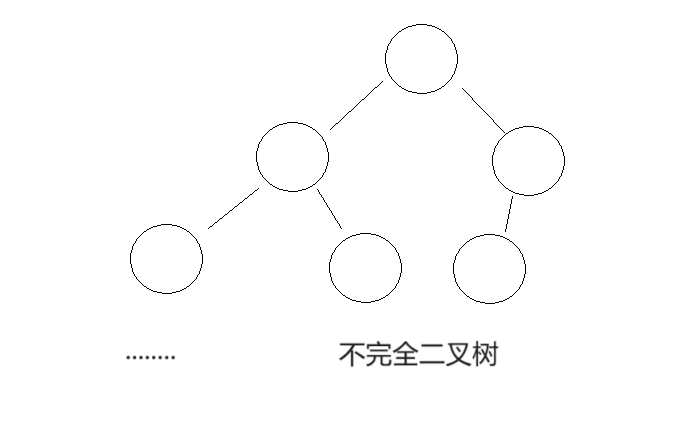
现实中的二叉树:


现实中的树,就是我们学过的二叉树倒过来的样子,大家可以把手机屏幕倒过来看试试。
🍍二叉树的存储结构
二叉树分为顺序存储和链式存储

顺序存储:类似于数组的存储形式,但只有完全二叉树才会用顺序存储,这样才不会造成空间的浪费

链式存储:利用了链表的性质。每个节点都存储了上个树和下个树的位置,这也就是带头指针的双链表结构
🍑堆
🍍堆的含义
堆是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象。堆总是满足下列性质:
(1)堆中某个结点的值总是不大于或不小于其父结点的值;
(2)堆总是一棵完全二叉树。
(3)将根结点最大的堆叫做最大堆或大根堆,根结点最小的堆叫做最小堆或小根堆。常见的堆有 二叉堆、斐波那契堆等。
(4)堆的物理结构本质上是顺序存储的,是线性的。但在逻辑上不是线性的,是完全二叉树的这种逻辑储存结构。 堆的这个数据结构,里面的成员包括一维数组,数组的容量,数组元素的个数,有两个直接后继。
🍍堆的结构
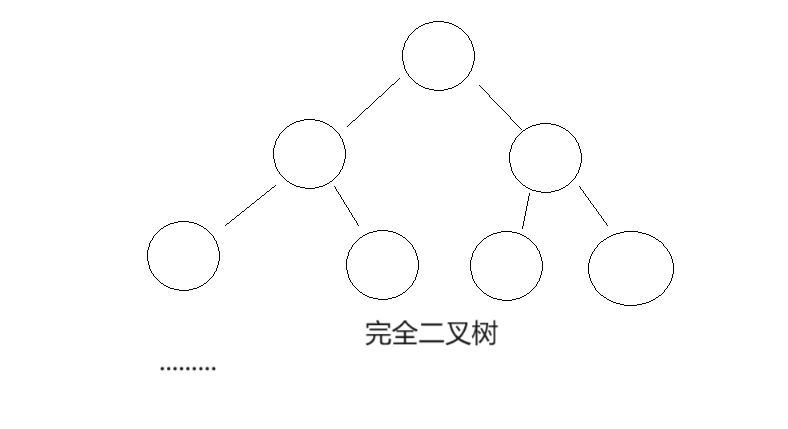
堆的结构就是特殊的二叉树结构,也就是上图中完全二叉树的样子
🍍堆的实现

堆的实现又分为大堆和小堆
大堆:任何父节点都大于等于子节点。
小堆:任何父节点都小于等于子节点。
两个子节点之间的大小没有明确规定
🍌补充条件
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>typedef int HPDatetype;
typedef struct Heap
{HPDatetype* a;int catacity;int size;
}HP;void Swap(HPDatetype *a1, HPDatetype *a2)
{HPDatetype cur = *a1;*a1 = *a2;*a2 = cur;
}
Swap()函数是交换两个数的作用,是利用结构体形式创建的堆
🍌堆的初始化
void HeapInia(HP* ps)
{assert(ps);//防止堆为空ps->a = NULL;ps->size = ps->catacity = 0;
}
🍌堆的销毁
void HeapDestroy(HP* ps)
{assert(ps);//防止堆为空free(ps->a);ps->a = NULL;ps->size = 0;ps->catacity = 0;
}
🍌堆的插入
void AdjustUp(HPDatetype* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (parent - 1) / 2;}else{break;}}
}void HeapPush(HP* ps, HPDatetype x)
{assert(ps);//防止堆为空if (ps->catacity == ps->size){if (ps->catacity == 0){ps->catacity = 2;}else{ps->catacity *= 2;}int newcatacity = ps->catacity;HPDatetype* cur = (HPDatetype*)realloc(ps->a, sizeof(HPDatetype) * newcatacity);if (cur == NULL){perror("realloc fail");exit(-1);}ps->a = cur;ps->catacity = newcatacity;}ps->a[ps->size] = x;(ps->size)++;AdjustUp(ps->a, ps->size - 1);
}
AdjustUp()函数是把子节点向上调整的作用,因为我们利用数组形式建立堆,只能分为大堆和小堆,所以需要重新设计一个函数来调整子节点的位置。在这里我们是创建小堆。关于怎么向上找父节点,是利用了数组的位置特性。数组是从0开始,大家就可以找规律,以父节点找子节点就是需要加1再除以2,以子节点找父节点就是减1除以2。
🍌 堆的删除
void AdjustLown(HPDatetype* a, int n, int parent)//向下调整
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child] > a[child + 1]){child++;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}void HeapPop(HP* ps)
{assert(ps);assert(ps->size > 0);Swap(&(ps->a[0]), &(ps->a[ps->size - 1]));(ps->size)--;AdjustLown(ps->a, ps->size, 0);//向下调整}
堆的删除,在这里我们是删除的堆顶数据。
首先我们是先把堆顶数据和堆尾数据交换,然后再删除堆顶数据,最后利用函数AdjustLown()进行向下调整就行。
如果是小堆,取出来的数据就是依次变大,相反是大堆,取出来的数据就是依次变小。
堆在这里还有一个应用,就是堆排序。小堆就是升序,大堆就是降序。
🍌取堆顶的数据
HPDatetype HeapTop(HP* ps)
{assert(ps);assert(ps->size > 0);return ps->a[0];
}
返回堆顶数据即可
🍌堆的数据个数
int HeapSize(HP* ps)
{return ps->size;
}
直接返回ps->size即可
🍌堆的判空
bool HeapEmpty(HP* ps)
{assert(ps);return ps->size == 0;
}
注意,这里判空用到bool需要头文件名#include<stdbool.h>
🍌堆的整体代码实现
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>typedef int HPDatetype;
typedef struct Heap
{HPDatetype* a;int catacity;int size;
}HP;void HeapInia(HP* ps)
{assert(ps);ps->a = NULL;ps->catacity = ps->size = 0;
}void HeapDestroy(HP* ps)
{assert(ps);free(ps->a);ps->a = NULL;ps->size = ps->catacity;
}void Swap(HPDatetype* a1, HPDatetype* a2)
{HPDatetype cur = *a1;*a1 = *a2;*a2 = cur;
}void AdjustUp(HPDatetype* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (parent - 1) / 2;}else{break;}}
}void HeapPush(HP* ps, HPDatetype x)
{assert(ps);if (ps->size == ps->catacity){if (ps->catacity == 0)ps->catacity = 2;elseps->catacity *= 2;int newcatacity = ps->catacity;HPDatetype* cur = (HPDatetype*)realloc(ps->a, sizeof(HPDatetype) * newcatacity);if (cur == NULL){perror("realloc fail");exit(-1);}ps->a = cur;ps->catacity = newcatacity;}ps->a[ps->size] = x;(ps->size)++;AdjustUp(ps->a, ps->size - 1);}void AdjustLown(HPDatetype* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child] > a[child + 1]){child++;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}void HeapPop(HP* ps)
{assert(ps);assert(ps->size > 0);Swap(&(ps->a[0]), &(ps->a[ps->size - 1]));(ps->size)--;AdjustLown(ps->a, ps->size, 0);}HPDatetype HeapTop(HP* ps)
{assert(ps);assert(ps->size > 0);return ps->a[0];
}int HeapSize(HP* ps)
{return ps->size;
}bool HeapEmpty(HP* ps)
{assert(ps);return ps->size == 0;
}void HeapPrint(HP *ps)
{for (int i = 0; i < ps->size; i++){printf("%d ", ps->a[i]);}printf("\n");
}int main()
{int a[] = { 65,100,70,32,50,60 };int size = sizeof(a) / sizeof(a[0]);HP ps;HeapInia(&ps);for (int i = 0; i < size; i++){HeapPush(&ps, a[i]);}HeapPrint(&ps);int net = HeapSize(&ps);//堆排序while (!HeapEmpty(&ps)){printf("%d ", HeapTop(&ps));HeapPop(&ps);}printf("%d ", net);HeapDestroy(&ps);return 0;
}
上面我也不充了堆排序,大家有兴趣可以试试,由于我这里是建的小堆,所以排出来的序是升序。
有不足的地方欢迎大家指正,谢谢!!!

相关文章:

堆和二叉树的动态实现(C语言实现)
✅✅✅✅✅✅✅✅✅✅✅✅✅✅✅✅ ✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨ 🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿…...
Vue前端+快速入门【详解】
目录 1.Vue概述 2. 快速入门 3. Vue指令 4.表格信息案例 5. 生命周期 1.Vue概述 1.MVVM思想 原始HTMLCSSJavaScript开发存在的问题:操作麻烦,耦合性强 为了实现html标签与数据的解耦,前端开发中提供了MVVM思想:即Model-Vi…...
day06_菜单管理(查询菜单,添加菜单,添加子菜单,修改菜单,删除菜单,角色分配菜单,查询菜单,保存菜单,动态菜单)
文章目录 1 菜单管理1.1 表结构介绍1.2 查询菜单1.2.1 需求说明1.2.2 页面制作1.2.3 后端接口SysMenuSysMenuControllerSysMenuServiceMenuHelperSysMenuMapperSysMenuMapper.xml 1.2.4 前端对接sysMenu.jssysMenu.vue 1.3 添加菜单1.3.1 需求说明1.3.3 页面制作1.3.3 后端接口…...

探究与以太坊智能合约的交互
# 概述 智能合约是部署在区块链上的一串代代码,通常我们与智能合约的打交道 可以通过前端的Dapp,etherscan,metamask 等方式。作为开发人员可以通过调用提供的相关包来与之交互,如web3.js,ether.js , web3.j(java 语言…...
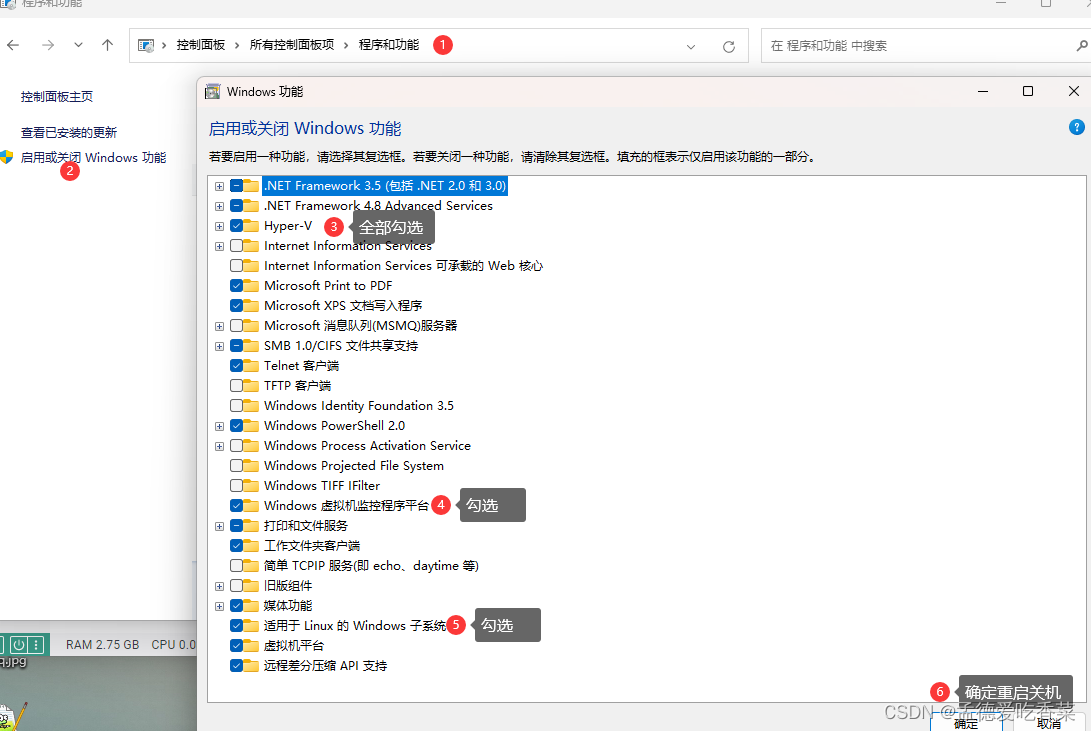
Windows如何安装docker-desktop
下载 docker-desktop设置环境安装wsl可能遇到的错误 下载 docker-desktop 下载官网:https://www.docker.com/products/docker-desktop/ 设置环境 如果没有Hyper-V选项的,按照以下步骤 添加一个文件Hyper-V.bat 添加以下内容,并双击运行后重启电脑 pushd "%~…...

芯片设计后端遇到的各种文件类型和文件后缀
芯片设计后端遇到的各种文件类型和文件后缀 文件类型 描述 文件后缀 netlist网表文件 verilog文件格式,记录了芯片里各个instance的逻辑连接关系 .v (for Verilog netlists) Lib,liberty timing file 记录了cell的timing信息及一定power信息。有的…...

【Web】Java反序列化之CC7链——Hashtable
目录 链子原理分析(借尸还魂) 如何构造相等hash 又谈为何lazyMap2.remove("yy") 不过真的需要两个LazyMap吗 EXP 双LazyMap exp HashMap&LazyMap exp 链子原理分析(借尸还魂) 先看Hashtable#readObject origlength和elements分别是原始数组的长度和元素…...

NumPy数据处理详解的笔记2
NumPy数据处理详解的笔记2 第1章NumPy基础 NumPy是用于处理多维数组的数值运算库,不仅可用于 机器学习,还可以用于图像处理,语言处理等任务。 1.2 多维数据结构ndarray的基础 在学习NumPy的过程中,只要理解了ndarray的相关知识…...
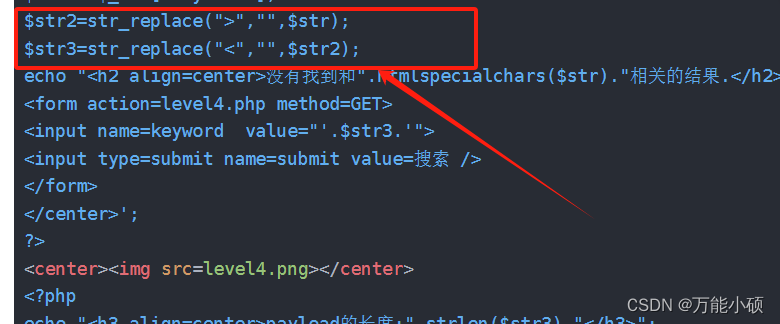
xsslabs第四关
测试 "onclick"alert(1) 这与第三关的代码是一样的,但是每一关考的点是不一样的所以我们看一下源代码 <!DOCTYPE html><!--STATUS OK--><html> <head> <meta http-equiv"content-type" content"text/html;ch…...
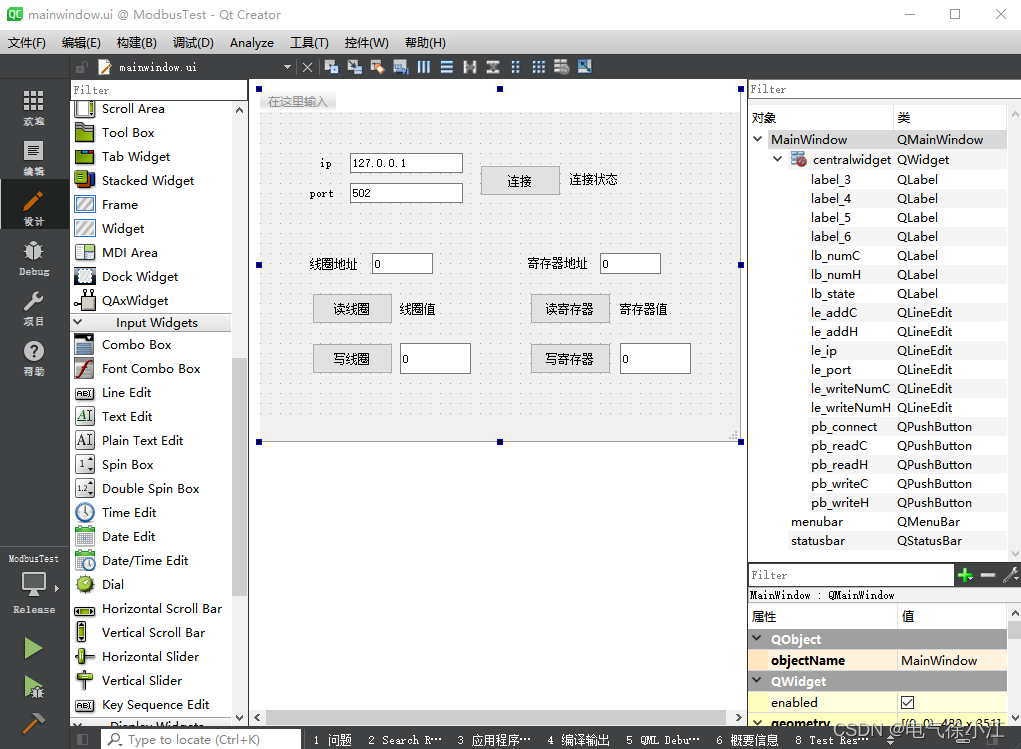
Qt下使用modbus-c库实现PLC线圈/保持寄存器的读写
系列文章目录 提示:这里是该系列文章的所有文章的目录 第一章:Qt下使用ModbusTcp通信协议进行PLC线圈/保持寄存器的读写(32位有符号数) 第二章:Qt下使用modbus-c库实现PLC线圈/保持寄存器的读写 文章目录 系列文章目录…...

C++ 滑动窗口
例1 209. 长度最小的子数组 ①窗口大小不固定 ②求最小长度 -> ret INT_MAX ③数组内的值都大于0, 符合单调性(sum nums[right] -> sum增大) while里面符合条件,在里面更改ret 参考代码 class Solution { public:i…...

【深度学习】TensorFlow基础介绍
TensorFlow 模型 张量、变量共同点:具有形状、类型、值等3个属性。 不同点:变量可被TensorFlow的自动求导机制求导,常被用于机器学习模型的参数。 tfrecord tensorflow定义的数据格式,一种二进制文件格式,用于保存…...

springcloud:3.3测试重试机制
服务提供者【test-provider8001】 Openfeign远程调用服务提供者搭建 文章地址http://t.csdnimg.cn/06iz8 相关接口 测试远程调用:http://localhost:8001/payment/index 服务消费者【test-consumer-resilience4j8004】 Openfeign远程调用消费者搭建 文章地址http:/…...

【笔记】【电子科大 离散数学】 3.谓词逻辑
谓词引入 因为含变量的语句(例如x > 3)不是命题,无法进行逻辑推理。 为了研究简单命题句子内部的逻辑关系,我们需要对简单命题进行分解,利用个体词,谓词和量词来描述它们,并研究个体与总体…...

倍增算法C++
倍增 倍增算法是一种优化算法,通常用于某些需要高效计算指数幂的场景。它基于分治的思想,通过反复求平方来实现快速计算指数幂的目的。在实际应用中,倍增算法经常用于解决最近公共祖先问题、二分查找等。 1、快速幂详解 ksm核心代码 倍增就是…...

uniapp制作--进步器的选择
介绍: 进步器的选择,一般用于商城购物选择物品数量的场景 注意:该输入框只能输入大于或等于0的整数 效果展示: 代码展示: 以下是一个简单的购物车页面示例,包括选择商品和显示数量的功能: 在这个示例中…...

前端高频面试--查缺补漏篇
什么是进程和线程,有什么区别 进程:进程是程序的一次执行过程,是动态的过程,有自身产生、存在、消亡的过程。 线程:线程由进程创建,是进程的一个实体。一个进程可以拥有多个线程。 举个例子:…...

【计算机学习】-- 网页视频加速
系列文章目录 文章目录 系列文章目录前言一、开发者选项二、定义和用法1.基础语法:2.什么是uncaught TypeError:Cannot read properties of null? 二、开发者工具面板:1.Elements面板:2.Console面板: 总结 前言 一、开发者选项 …...

系统运维-Linux配置C、C++、Go语言编译环境
C yum install gcc -y #安装gcc编译器 gcc --version #验证环境gcc (GCC) 11.3.1 20221121 (Red Hat 11.3.1-4) Copyright (C) 2021 Free Software Foundation, Inc. This is free software; see the source for copying conditions. There is NO warranty; not even f…...
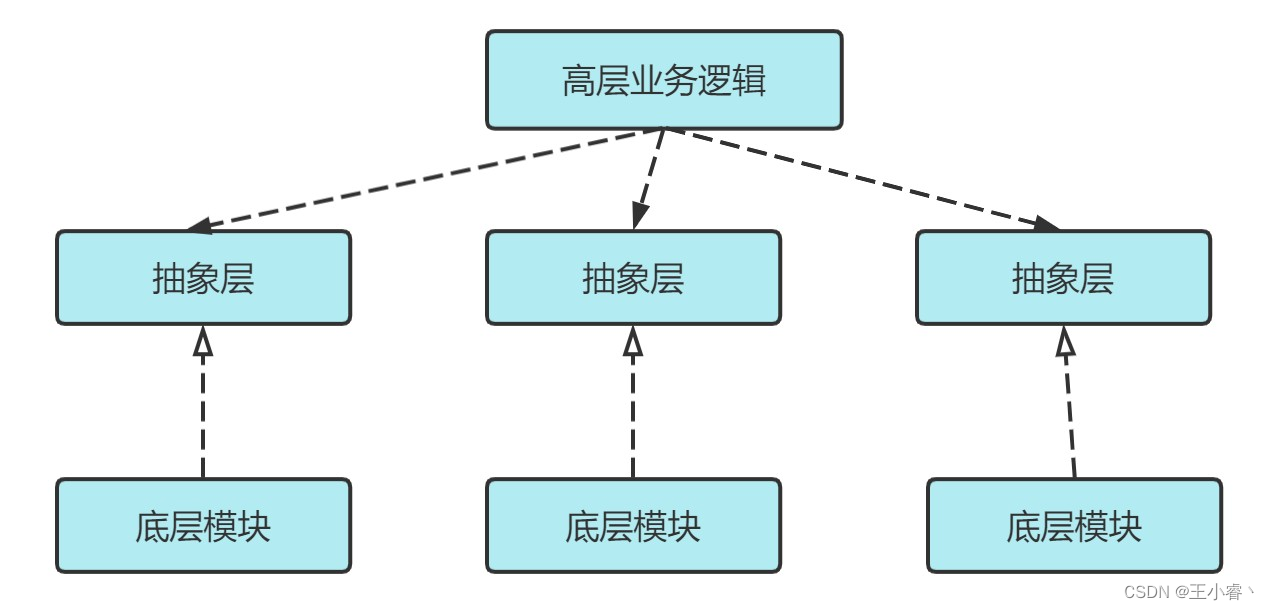
【设计模式】(二)设计模式六大设计原则
一、 设计原则概述 设计模式中主要有六大设计原则,简称为SOLID ,是由于各个原则的首字母简称合并的来(两个L算一个,solid 稳定的),六大设计原则分别如下: 1、单一职责原则(Single Responsibitity Principle&#…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...
