C语言数据结构与算法——深度、广度优先搜索(DFS、BFS)
目录
一、深度优先搜索(Depth-First-Search 简称:DFS)
无向图的深度优先搜索
有向图的深度优先搜索
二、广度优先搜索(Breadth-First-Search 简称:BFS)
无向图的广度优先搜索
有向图的广度优先搜索
深度优先搜索(Depth-First Search,DFS)和广度优先搜索(Breadth-First Search,BFS)是两种常见的图遍历算法,它们在C语言中被广泛应用于解决各种数据结构和算法问题。这两种搜索算法都用于遍历图或树中的节点,以便查找特定的目标或执行其他相关任务。
一、深度优先搜索(Depth-First-Search 简称:DFS)
图的深度优先搜索(Depth First Search),和树的先序遍历比较类似。
它的思想:假设初始状态是图中所有顶点均未被访问,则从某个顶点v出发,首先访问该顶点,然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图,直至图中所有和v有路径相通的顶点都被访问到。 若此时尚有其他顶点未被访问到,则另选一个未被访问的顶点作起始点,重复上述过程,直至图中所有顶点都被访问到为止。
显然,深度优先搜索是一个递归的过程。
无向图的深度优先搜索
1.1 遍历过程:
(1)从图中某个顶点v出发,访问v。
(2)找出刚才第一个被顶点访问的邻接点。访问该顶点。以这个顶点为新的顶点,重复此步骤,直到访问过的顶点没有未被访问过的顶点为止。
(3)返回到步骤(2)中的被顶点v访问的,且还没被访问的邻接点,找出该点的下一个未被访问的邻接点,访问该顶点。
(4)重复(2) (3) 直到每个点都被访问过,遍历结束。
例无权图: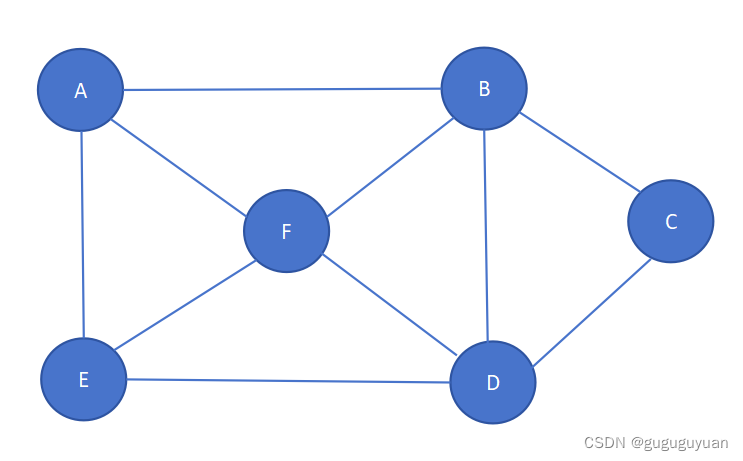
第1步:访问A。
第2步:访问(A的邻接点)B。 在第1步访问A之后,接下来应该访问的是A的邻接点,即"B、F、E"中的一个。但在本文的实现中,顶点ABCDEFG是按照顺序存储,B在"D、F和E"的前面,因此,先访问B。
第3步:访问(B的邻接点)C。在第2步访问B之后,接下来应该访问B的邻接点,即"F、D、C"中一个(A已经被访问过,就不算在内)。而由于C在D、F之前,先访问C。
第4步:访问(C的邻接点)D。在第3步访问C之后,接下来应该访问C的邻接点,即D。(B已经被访问过,就不算在内)。
第5步:访问(D的邻接点)E。
第6步:访问(E的邻接点)F。
故遍历结果为 A->B->C->D->E->F

有向图的深度优先搜索
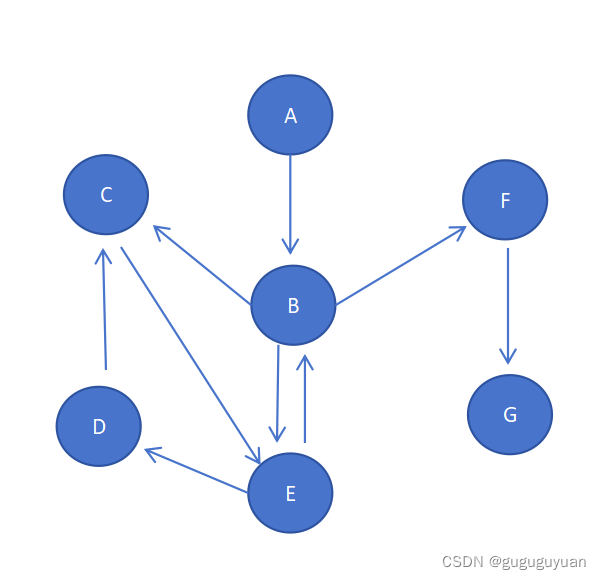
第1步:访问A。
第2步:访问B。在访问A之后,接下来访问A的出边的另一个顶点,即顶点B。
第3步:访问C。 在访问了B之后,接下来应该访问的是B的出边的另一个顶点,即顶点C,E,F。在本文实现的图中,顶点ABCDEFG按照顺序存储,因此先访问C。
第4步:访问E。接下来访问C的出边的另一个顶点,即顶点E。
第5步:访问D。接下来访问E的出边的另一个顶点,即顶点B,D。顶点B已经被访问过,因此访问顶点D。
第6步:访问F。接下应该回溯"访问A的出边的另一个顶点F"。
第7步:访问G。
故遍历结果为A->b->c->E->D->F->G
二、广度优先搜索(Breadth-First-Search 简称:BFS)
广度优先搜索算法(Breadth First Search),又称为"宽度优先搜索"或"横向优先搜索",简称BFS。
它的思想是:从图中某顶点v出发,在访问了v之后依次访问v的各个未曾访问过的邻接点,然后分别从这些邻接点出发依次访问它们的邻接点,并使得“先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问,直至图中所有已被访问的顶点的邻接点都被访问到。如果此时图中尚有顶点未被访问,则需要另选一个未曾被访问过的顶点作为新的起始点,重复上述过程,直至图中所有顶点都被访问到为止。
换句话说,广度优先搜索遍历图的过程是以v为起点,由近至远,依次访问和v有路径相通且路径长度为1,2...的顶点。
无向图的广度优先搜索

第1步:访问A。
第2步:依次访问B,E,F。
在访问了A之后,接下来访问A的邻接点。顶点ABCDEFG按照顺序存储,B在"E和F"的前面,因此,先访问B。再访问完B之后,再依次访问E,F。
第3步:依次访问C,D。
在第2步访问完B,E,F之后,再依次访问它们的邻接点。首先访问B的邻接点C,再访问E的邻接点D。
因此访问顺序是:A->B->E->F->C->D
有向图的广度优先搜索
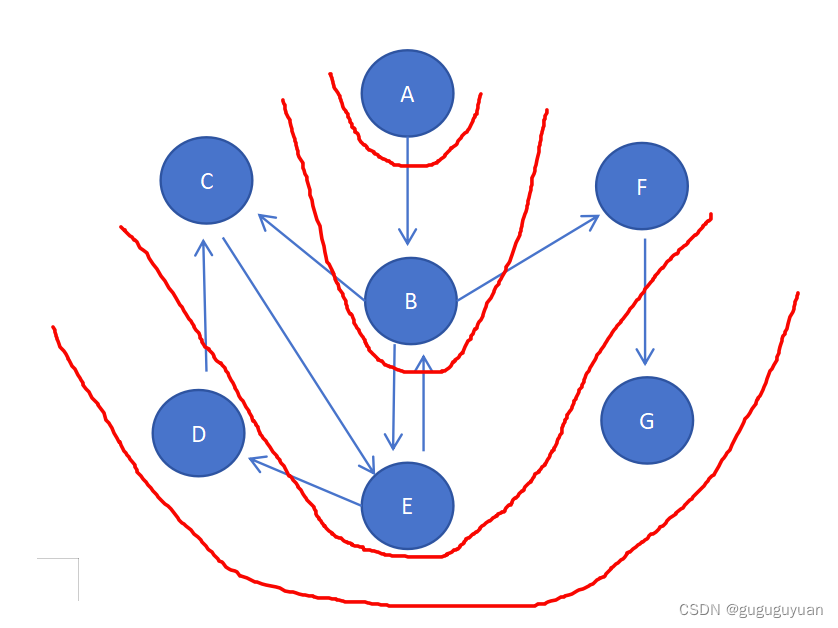
第1步:访问A。
第2步:访问B。
第3步:依次访问C,E,F。
在访问了B之后,接下来访问B的出边的另一个顶点,即C,E,F。顶点ABCDEFG按照顺序存储,因此会先访问C,再依次访问E,F。
第4步:依次访问D,G。
在访问完C,E,F之后,再依次访问它们的出边的另一个顶点。还是按照C,E,F的顺序访问,C的已经全部访问过了,那么就只剩下E,F;先访问E的邻接点D,再访问F的邻接点G。
因此访问顺序是:A->B->C->E->F->D->G
邻接矩阵图表示的"无向图"
/*** C: 邻接矩阵图表示的"无向图(Matrix Undirected Graph)"** @author skywang* @date 2014/04/18*/#include <stdio.h>
#include <stdlib.h>
#include <malloc.h>
#include <string.h>#define MAX 100
#define isLetter(a) ((((a)>='a')&&((a)<='z')) || (((a)>='A')&&((a)<='Z')))
#define LENGTH(a) (sizeof(a)/sizeof(a[0]))// 邻接矩阵
typedef struct _graph
{char vexs[MAX]; // 顶点集合int vexnum; // 顶点数int edgnum; // 边数int matrix[MAX][MAX]; // 邻接矩阵
}Graph, *PGraph;/** 返回ch在matrix矩阵中的位置*/
static int get_position(Graph g, char ch)
{int i;for(i=0; i<g.vexnum; i++)if(g.vexs[i]==ch)return i;return -1;
}/** 读取一个输入字符*/
static char read_char()
{char ch;do {ch = getchar();} while(!isLetter(ch));return ch;
}/** 创建图(自己输入)*/
Graph* create_graph()
{char c1, c2;int v, e;int i, p1, p2;Graph* pG;// 输入"顶点数"和"边数"printf("input vertex number: ");scanf("%d", &v);printf("input edge number: ");scanf("%d", &e);if ( v < 1 || e < 1 || (e > (v * (v-1)))){printf("input error: invalid parameters!\n");return NULL;}if ((pG=(Graph*)malloc(sizeof(Graph))) == NULL )return NULL;memset(pG, 0, sizeof(Graph));// 初始化"顶点数"和"边数"pG->vexnum = v;pG->edgnum = e;// 初始化"顶点"for (i = 0; i < pG->vexnum; i++){printf("vertex(%d): ", i);pG->vexs[i] = read_char();}// 初始化"边"for (i = 0; i < pG->edgnum; i++){// 读取边的起始顶点和结束顶点printf("edge(%d):", i);c1 = read_char();c2 = read_char();p1 = get_position(*pG, c1);p2 = get_position(*pG, c2);if (p1==-1 || p2==-1){printf("input error: invalid edge!\n");free(pG);return NULL;}pG->matrix[p1][p2] = 1;pG->matrix[p2][p1] = 1;}return pG;
}/** 创建图(用已提供的矩阵)*/
Graph* create_example_graph()
{char vexs[] = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};char edges[][2] = {{'A', 'C'}, {'A', 'D'}, {'A', 'F'}, {'B', 'C'}, {'C', 'D'}, {'E', 'G'}, {'F', 'G'}}; int vlen = LENGTH(vexs);int elen = LENGTH(edges);int i, p1, p2;Graph* pG;// 输入"顶点数"和"边数"if ((pG=(Graph*)malloc(sizeof(Graph))) == NULL )return NULL;memset(pG, 0, sizeof(Graph));// 初始化"顶点数"和"边数"pG->vexnum = vlen;pG->edgnum = elen;// 初始化"顶点"for (i = 0; i < pG->vexnum; i++){pG->vexs[i] = vexs[i];}// 初始化"边"for (i = 0; i < pG->edgnum; i++){// 读取边的起始顶点和结束顶点p1 = get_position(*pG, edges[i][0]);p2 = get_position(*pG, edges[i][1]);pG->matrix[p1][p2] = 1;pG->matrix[p2][p1] = 1;}return pG;
}/** 返回顶点v的第一个邻接顶点的索引,失败则返回-1*/
static int first_vertex(Graph G, int v)
{int i;if (v<0 || v>(G.vexnum-1))return -1;for (i = 0; i < G.vexnum; i++)if (G.matrix[v][i] == 1)return i;return -1;
}/** 返回顶点v相对于w的下一个邻接顶点的索引,失败则返回-1*/
static int next_vertix(Graph G, int v, int w)
{int i;if (v<0 || v>(G.vexnum-1) || w<0 || w>(G.vexnum-1))return -1;for (i = w + 1; i < G.vexnum; i++)if (G.matrix[v][i] == 1)return i;return -1;
}/** 深度优先搜索遍历图的递归实现*/
static void DFS(Graph G, int i, int *visited)
{ int w; visited[i] = 1;printf("%c ", G.vexs[i]);// 遍历该顶点的所有邻接顶点。若是没有访问过,那么继续往下走for (w = first_vertex(G, i); w >= 0; w = next_vertix(G, i, w)){if (!visited[w])DFS(G, w, visited);}}/** 深度优先搜索遍历图*/
void DFSTraverse(Graph G)
{int i;int visited[MAX]; // 顶点访问标记// 初始化所有顶点都没有被访问for (i = 0; i < G.vexnum; i++)visited[i] = 0;printf("DFS: ");for (i = 0; i < G.vexnum; i++){//printf("\n== LOOP(%d)\n", i);if (!visited[i])DFS(G, i, visited);}printf("\n");
}/** 广度优先搜索(类似于树的层次遍历)*/
void BFS(Graph G)
{int head = 0;int rear = 0;int queue[MAX]; // 辅组队列int visited[MAX]; // 顶点访问标记int i, j, k;for (i = 0; i < G.vexnum; i++)visited[i] = 0;printf("BFS: ");for (i = 0; i < G.vexnum; i++){if (!visited[i]){visited[i] = 1;printf("%c ", G.vexs[i]);queue[rear++] = i; // 入队列}while (head != rear) {j = queue[head++]; // 出队列for (k = first_vertex(G, j); k >= 0; k = next_vertix(G, j, k)) //k是为访问的邻接顶点{if (!visited[k]){visited[k] = 1;printf("%c ", G.vexs[k]);queue[rear++] = k;}}}}printf("\n");
}/** 打印矩阵队列图*/
void print_graph(Graph G)
{int i,j;printf("Martix Graph:\n");for (i = 0; i < G.vexnum; i++){for (j = 0; j < G.vexnum; j++)printf("%d ", G.matrix[i][j]);printf("\n");}
}void main()
{Graph* pG;// 自定义"图"(输入矩阵队列)//pG = create_graph();// 采用已有的"图"pG = create_example_graph();print_graph(*pG); // 打印图DFSTraverse(*pG); // 深度优先遍历BFS(*pG); // 广度优先遍历
}邻接表表示的"无向图"
/*** C: 邻接表表示的"无向图(List Undirected Graph)"** @author skywang* @date 2014/04/18*/#include <stdio.h>
#include <stdlib.h>
#include <malloc.h>
#include <string.h>#define MAX 100
#define isLetter(a) ((((a)>='a')&&((a)<='z')) || (((a)>='A')&&((a)<='Z')))
#define LENGTH(a) (sizeof(a)/sizeof(a[0]))// 邻接表中表对应的链表的顶点
typedef struct _ENode
{int ivex; // 该边所指向的顶点的位置struct _ENode *next_edge; // 指向下一条弧的指针
}ENode, *PENode;// 邻接表中表的顶点
typedef struct _VNode
{char data; // 顶点信息ENode *first_edge; // 指向第一条依附该顶点的弧
}VNode;// 邻接表
typedef struct _LGraph
{int vexnum; // 图的顶点的数目int edgnum; // 图的边的数目VNode vexs[MAX];
}LGraph;/** 返回ch在matrix矩阵中的位置*/
static int get_position(LGraph g, char ch)
{int i;for(i=0; i<g.vexnum; i++)if(g.vexs[i].data==ch)return i;return -1;
}/** 读取一个输入字符*/
static char read_char()
{char ch;do {ch = getchar();} while(!isLetter(ch));return ch;
}/** 将node链接到list的末尾*/
static void link_last(ENode *list, ENode *node)
{ENode *p = list;while(p->next_edge)p = p->next_edge;p->next_edge = node;
}/** 创建邻接表对应的图(自己输入)*/
LGraph* create_lgraph()
{char c1, c2;int v, e;int i, p1, p2;ENode *node1, *node2;LGraph* pG;// 输入"顶点数"和"边数"printf("input vertex number: ");scanf("%d", &v);printf("input edge number: ");scanf("%d", &e);if ( v < 1 || e < 1 || (e > (v * (v-1)))){printf("input error: invalid parameters!\n");return NULL;}if ((pG=(LGraph*)malloc(sizeof(LGraph))) == NULL )return NULL;memset(pG, 0, sizeof(LGraph));// 初始化"顶点数"和"边数"pG->vexnum = v;pG->edgnum = e;// 初始化"邻接表"的顶点for(i=0; i<pG->vexnum; i++){printf("vertex(%d): ", i);pG->vexs[i].data = read_char();pG->vexs[i].first_edge = NULL;}// 初始化"邻接表"的边for(i=0; i<pG->edgnum; i++){// 读取边的起始顶点和结束顶点printf("edge(%d): ", i);c1 = read_char();c2 = read_char();p1 = get_position(*pG, c1);p2 = get_position(*pG, c2);// 初始化node1node1 = (ENode*)malloc(sizeof(ENode));node1->ivex = p2;// 将node1链接到"p1所在链表的末尾"if(pG->vexs[p1].first_edge == NULL)pG->vexs[p1].first_edge = node1;elselink_last(pG->vexs[p1].first_edge, node1);// 初始化node2node2 = (ENode*)malloc(sizeof(ENode));node2->ivex = p1;// 将node2链接到"p2所在链表的末尾"if(pG->vexs[p2].first_edge == NULL)pG->vexs[p2].first_edge = node2;elselink_last(pG->vexs[p2].first_edge, node2);}return pG;
}/** 创建邻接表对应的图(用已提供的数据)*/
LGraph* create_example_lgraph()
{char c1, c2;char vexs[] = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};char edges[][2] = {{'A', 'C'}, {'A', 'D'}, {'A', 'F'}, {'B', 'C'}, {'C', 'D'}, {'E', 'G'}, {'F', 'G'}}; int vlen = LENGTH(vexs);int elen = LENGTH(edges);int i, p1, p2;ENode *node1, *node2;LGraph* pG;if ((pG=(LGraph*)malloc(sizeof(LGraph))) == NULL )return NULL;memset(pG, 0, sizeof(LGraph));// 初始化"顶点数"和"边数"pG->vexnum = vlen;pG->edgnum = elen;// 初始化"邻接表"的顶点for(i=0; i<pG->vexnum; i++){pG->vexs[i].data = vexs[i];pG->vexs[i].first_edge = NULL;}// 初始化"邻接表"的边for(i=0; i<pG->edgnum; i++){// 读取边的起始顶点和结束顶点c1 = edges[i][0];c2 = edges[i][1];p1 = get_position(*pG, c1);p2 = get_position(*pG, c2);// 初始化node1node1 = (ENode*)malloc(sizeof(ENode));node1->ivex = p2;// 将node1链接到"p1所在链表的末尾"if(pG->vexs[p1].first_edge == NULL)pG->vexs[p1].first_edge = node1;elselink_last(pG->vexs[p1].first_edge, node1);// 初始化node2node2 = (ENode*)malloc(sizeof(ENode));node2->ivex = p1;// 将node2链接到"p2所在链表的末尾"if(pG->vexs[p2].first_edge == NULL)pG->vexs[p2].first_edge = node2;elselink_last(pG->vexs[p2].first_edge, node2);}return pG;
}/** 深度优先搜索遍历图的递归实现*/
static void DFS(LGraph G, int i, int *visited)
{int w;ENode *node;visited[i] = 1;printf("%c ", G.vexs[i].data);node = G.vexs[i].first_edge;while (node != NULL){if (!visited[node->ivex])DFS(G, node->ivex, visited);node = node->next_edge;}
}/** 深度优先搜索遍历图*/
void DFSTraverse(LGraph G)
{int i;int visited[MAX]; // 顶点访问标记// 初始化所有顶点都没有被访问for (i = 0; i < G.vexnum; i++)visited[i] = 0;printf("DFS: ");for (i = 0; i < G.vexnum; i++){if (!visited[i])DFS(G, i, visited);}printf("\n");
}/** 广度优先搜索(类似于树的层次遍历)*/
void BFS(LGraph G)
{int head = 0;int rear = 0;int queue[MAX]; // 辅组队列int visited[MAX]; // 顶点访问标记int i, j, k;ENode *node;for (i = 0; i < G.vexnum; i++)visited[i] = 0;printf("BFS: ");for (i = 0; i < G.vexnum; i++){if (!visited[i]){visited[i] = 1;printf("%c ", G.vexs[i].data);queue[rear++] = i; // 入队列}while (head != rear) {j = queue[head++]; // 出队列node = G.vexs[j].first_edge;while (node != NULL){k = node->ivex;if (!visited[k]){visited[k] = 1;printf("%c ", G.vexs[k].data);queue[rear++] = k;}node = node->next_edge;}}}printf("\n");
}/** 打印邻接表图*/
void print_lgraph(LGraph G)
{int i,j;ENode *node;printf("List Graph:\n");for (i = 0; i < G.vexnum; i++){printf("%d(%c): ", i, G.vexs[i].data);node = G.vexs[i].first_edge;while (node != NULL){printf("%d(%c) ", node->ivex, G.vexs[node->ivex].data);node = node->next_edge;}printf("\n");}
}void main()
{LGraph* pG;// 自定义"图"(自己输入数据)//pG = create_lgraph();// 采用已有的"图"pG = create_example_lgraph();// 打印图print_lgraph(*pG);DFSTraverse(*pG);BFS(*pG);
}邻接矩阵表示的"有向图"
/*** C: 邻接矩阵表示的"有向图(Matrix Directed Graph)"** @author skywang* @date 2014/04/18*/#include <stdio.h>
#include <stdlib.h>
#include <malloc.h>
#include <string.h>#define MAX 100
#define isLetter(a) ((((a)>='a')&&((a)<='z')) || (((a)>='A')&&((a)<='Z')))
#define LENGTH(a) (sizeof(a)/sizeof(a[0]))// 邻接矩阵
typedef struct _graph
{char vexs[MAX]; // 顶点集合int vexnum; // 顶点数int edgnum; // 边数int matrix[MAX][MAX]; // 邻接矩阵
}Graph, *PGraph;/** 返回ch在matrix矩阵中的位置*/
static int get_position(Graph g, char ch)
{int i;for(i=0; i<g.vexnum; i++)if(g.vexs[i]==ch)return i;return -1;
}/** 读取一个输入字符*/
static char read_char()
{char ch;do {ch = getchar();} while(!isLetter(ch));return ch;
}/** 创建图(自己输入)*/
Graph* create_graph()
{char c1, c2;int v, e;int i, p1, p2;Graph* pG;// 输入"顶点数"和"边数"printf("input vertex number: ");scanf("%d", &v);printf("input edge number: ");scanf("%d", &e);if ( v < 1 || e < 1 || (e > (v * (v-1)))){printf("input error: invalid parameters!\n");return NULL;}if ((pG=(Graph*)malloc(sizeof(Graph))) == NULL )return NULL;memset(pG, 0, sizeof(Graph));// 初始化"顶点数"和"边数"pG->vexnum = v;pG->edgnum = e;// 初始化"顶点"for (i = 0; i < pG->vexnum; i++){printf("vertex(%d): ", i);pG->vexs[i] = read_char();}// 初始化"边"for (i = 0; i < pG->edgnum; i++){// 读取边的起始顶点和结束顶点printf("edge(%d):", i);c1 = read_char();c2 = read_char();p1 = get_position(*pG, c1);p2 = get_position(*pG, c2);if (p1==-1 || p2==-1){printf("input error: invalid edge!\n");free(pG);return NULL;}pG->matrix[p1][p2] = 1;}return pG;
}/** 创建图(用已提供的矩阵)*/
Graph* create_example_graph()
{char vexs[] = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};char edges[][2] = {{'A', 'B'}, {'B', 'C'}, {'B', 'E'}, {'B', 'F'}, {'C', 'E'}, {'D', 'C'}, {'E', 'B'}, {'E', 'D'}, {'F', 'G'}}; int vlen = LENGTH(vexs);int elen = LENGTH(edges);int i, p1, p2;Graph* pG;// 输入"顶点数"和"边数"if ((pG=(Graph*)malloc(sizeof(Graph))) == NULL )return NULL;memset(pG, 0, sizeof(Graph));// 初始化"顶点数"和"边数"pG->vexnum = vlen;pG->edgnum = elen;// 初始化"顶点"for (i = 0; i < pG->vexnum; i++){pG->vexs[i] = vexs[i];}// 初始化"边"for (i = 0; i < pG->edgnum; i++){// 读取边的起始顶点和结束顶点p1 = get_position(*pG, edges[i][0]);p2 = get_position(*pG, edges[i][1]);pG->matrix[p1][p2] = 1;}return pG;
}/** 返回顶点v的第一个邻接顶点的索引,失败则返回-1*/
static int first_vertex(Graph G, int v)
{int i;if (v<0 || v>(G.vexnum-1))return -1;for (i = 0; i < G.vexnum; i++)if (G.matrix[v][i] == 1)return i;return -1;
}/** 返回顶点v相对于w的下一个邻接顶点的索引,失败则返回-1*/
static int next_vertix(Graph G, int v, int w)
{int i;if (v<0 || v>(G.vexnum-1) || w<0 || w>(G.vexnum-1))return -1;for (i = w + 1; i < G.vexnum; i++)if (G.matrix[v][i] == 1)return i;return -1;
}/** 深度优先搜索遍历图的递归实现*/
static void DFS(Graph G, int i, int *visited)
{ int w; visited[i] = 1;printf("%c ", G.vexs[i]);// 遍历该顶点的所有邻接顶点。若是没有访问过,那么继续往下走for (w = first_vertex(G, i); w >= 0; w = next_vertix(G, i, w)){if (!visited[w])DFS(G, w, visited);}}/** 深度优先搜索遍历图*/
void DFSTraverse(Graph G)
{int i;int visited[MAX]; // 顶点访问标记// 初始化所有顶点都没有被访问for (i = 0; i < G.vexnum; i++)visited[i] = 0;printf("DFS: ");for (i = 0; i < G.vexnum; i++){//printf("\n== LOOP(%d)\n", i);if (!visited[i])DFS(G, i, visited);}printf("\n");
}/** 广度优先搜索(类似于树的层次遍历)*/
void BFS(Graph G)
{int head = 0;int rear = 0;int queue[MAX]; // 辅组队列int visited[MAX]; // 顶点访问标记int i, j, k;for (i = 0; i < G.vexnum; i++)visited[i] = 0;printf("BFS: ");for (i = 0; i < G.vexnum; i++){if (!visited[i]){visited[i] = 1;printf("%c ", G.vexs[i]);queue[rear++] = i; // 入队列}while (head != rear) {j = queue[head++]; // 出队列for (k = first_vertex(G, j); k >= 0; k = next_vertix(G, j, k)) //k是为访问的邻接顶点{if (!visited[k]){visited[k] = 1;printf("%c ", G.vexs[k]);queue[rear++] = k;}}}}printf("\n");
}/** 打印矩阵队列图*/
void print_graph(Graph G)
{int i,j;printf("Martix Graph:\n");for (i = 0; i < G.vexnum; i++){for (j = 0; j < G.vexnum; j++)printf("%d ", G.matrix[i][j]);printf("\n");}
}void main()
{Graph* pG;// 自定义"图"(输入矩阵队列)//pG = create_graph();// 采用已有的"图"pG = create_example_graph();print_graph(*pG); // 打印图DFSTraverse(*pG); // 深度优先遍历BFS(*pG); // 广度优先遍历
}邻接表表示的"有向图"
/*** C: 邻接表表示的"有向图(List Directed Graph)"** @author skywang* @date 2014/04/18*/#include <stdio.h>
#include <stdlib.h>
#include <malloc.h>
#include <string.h>#define MAX 100
#define isLetter(a) ((((a)>='a')&&((a)<='z')) || (((a)>='A')&&((a)<='Z')))
#define LENGTH(a) (sizeof(a)/sizeof(a[0]))// 邻接表中表对应的链表的顶点
typedef struct _ENode
{int ivex; // 该边所指向的顶点的位置struct _ENode *next_edge; // 指向下一条弧的指针
}ENode, *PENode;// 邻接表中表的顶点
typedef struct _VNode
{char data; // 顶点信息ENode *first_edge; // 指向第一条依附该顶点的弧
}VNode;// 邻接表
typedef struct _LGraph
{int vexnum; // 图的顶点的数目int edgnum; // 图的边的数目VNode vexs[MAX];
}LGraph;/** 返回ch在matrix矩阵中的位置*/
static int get_position(LGraph g, char ch)
{int i;for(i=0; i<g.vexnum; i++)if(g.vexs[i].data==ch)return i;return -1;
}/** 读取一个输入字符*/
static char read_char()
{char ch;do {ch = getchar();} while(!isLetter(ch));return ch;
}/** 将node链接到list的末尾*/
static void link_last(ENode *list, ENode *node)
{ENode *p = list;while(p->next_edge)p = p->next_edge;p->next_edge = node;
}/** 创建邻接表对应的图(自己输入)*/
LGraph* create_lgraph()
{char c1, c2;int v, e;int i, p1, p2;ENode *node1, *node2;LGraph* pG;// 输入"顶点数"和"边数"printf("input vertex number: ");scanf("%d", &v);printf("input edge number: ");scanf("%d", &e);if ( v < 1 || e < 1 || (e > (v * (v-1)))){printf("input error: invalid parameters!\n");return NULL;}if ((pG=(LGraph*)malloc(sizeof(LGraph))) == NULL )return NULL;memset(pG, 0, sizeof(LGraph));// 初始化"顶点数"和"边数"pG->vexnum = v;pG->edgnum = e;// 初始化"邻接表"的顶点for(i=0; i<pG->vexnum; i++){printf("vertex(%d): ", i);pG->vexs[i].data = read_char();pG->vexs[i].first_edge = NULL;}// 初始化"邻接表"的边for(i=0; i<pG->edgnum; i++){// 读取边的起始顶点和结束顶点printf("edge(%d): ", i);c1 = read_char();c2 = read_char();p1 = get_position(*pG, c1);p2 = get_position(*pG, c2);// 初始化node1node1 = (ENode*)malloc(sizeof(ENode));node1->ivex = p2;// 将node1链接到"p1所在链表的末尾"if(pG->vexs[p1].first_edge == NULL)pG->vexs[p1].first_edge = node1;elselink_last(pG->vexs[p1].first_edge, node1);}return pG;
}/** 创建邻接表对应的图(用已提供的数据)*/
LGraph* create_example_lgraph()
{char c1, c2;char vexs[] = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};char edges[][2] = {{'A', 'B'}, {'B', 'C'}, {'B', 'E'}, {'B', 'F'}, {'C', 'E'}, {'D', 'C'}, {'E', 'B'}, {'E', 'D'}, {'F', 'G'}}; int vlen = LENGTH(vexs);int elen = LENGTH(edges);int i, p1, p2;ENode *node1, *node2;LGraph* pG;if ((pG=(LGraph*)malloc(sizeof(LGraph))) == NULL )return NULL;memset(pG, 0, sizeof(LGraph));// 初始化"顶点数"和"边数"pG->vexnum = vlen;pG->edgnum = elen;// 初始化"邻接表"的顶点for(i=0; i<pG->vexnum; i++){pG->vexs[i].data = vexs[i];pG->vexs[i].first_edge = NULL;}// 初始化"邻接表"的边for(i=0; i<pG->edgnum; i++){// 读取边的起始顶点和结束顶点c1 = edges[i][0];c2 = edges[i][1];p1 = get_position(*pG, c1);p2 = get_position(*pG, c2);// 初始化node1node1 = (ENode*)malloc(sizeof(ENode));node1->ivex = p2;// 将node1链接到"p1所在链表的末尾"if(pG->vexs[p1].first_edge == NULL)pG->vexs[p1].first_edge = node1;elselink_last(pG->vexs[p1].first_edge, node1);}return pG;
}/** 深度优先搜索遍历图的递归实现*/
static void DFS(LGraph G, int i, int *visited)
{int w;ENode *node;visited[i] = 1;printf("%c ", G.vexs[i].data);node = G.vexs[i].first_edge;while (node != NULL){if (!visited[node->ivex])DFS(G, node->ivex, visited);node = node->next_edge;}
}/** 深度优先搜索遍历图*/
void DFSTraverse(LGraph G)
{int i;int visited[MAX]; // 顶点访问标记// 初始化所有顶点都没有被访问for (i = 0; i < G.vexnum; i++)visited[i] = 0;printf("DFS: ");for (i = 0; i < G.vexnum; i++){if (!visited[i])DFS(G, i, visited);}printf("\n");
}/** 广度优先搜索(类似于树的层次遍历)*/
void BFS(LGraph G)
{int head = 0;int rear = 0;int queue[MAX]; // 辅组队列int visited[MAX]; // 顶点访问标记int i, j, k;ENode *node;for (i = 0; i < G.vexnum; i++)visited[i] = 0;printf("BFS: ");for (i = 0; i < G.vexnum; i++){if (!visited[i]){visited[i] = 1;printf("%c ", G.vexs[i].data);queue[rear++] = i; // 入队列}while (head != rear) {j = queue[head++]; // 出队列node = G.vexs[j].first_edge;while (node != NULL){k = node->ivex;if (!visited[k]){visited[k] = 1;printf("%c ", G.vexs[k].data);queue[rear++] = k;}node = node->next_edge;}}}printf("\n");
}/** 打印邻接表图*/
void print_lgraph(LGraph G)
{int i,j;ENode *node;printf("List Graph:\n");for (i = 0; i < G.vexnum; i++){printf("%d(%c): ", i, G.vexs[i].data);node = G.vexs[i].first_edge;while (node != NULL){printf("%d(%c) ", node->ivex, G.vexs[node->ivex].data);node = node->next_edge;}printf("\n");}
}void main()
{LGraph* pG;// 自定义"图"(自己输入数据)//pG = create_lgraph();// 采用已有的"图"pG = create_example_lgraph();// 打印图print_lgraph(*pG);DFSTraverse(*pG);BFS(*pG);
}相关文章:

C语言数据结构与算法——深度、广度优先搜索(DFS、BFS)
目录 一、深度优先搜索(Depth-First-Search 简称:DFS) 无向图的深度优先搜索 有向图的深度优先搜索 二、广度优先搜索(Breadth-First-Search 简称:BFS) 无向图的广度优先搜索 有向图的广度优先搜索 深…...
Golang Channel 详细原理和使用技巧
1.简介 Channel(一般简写为 chan) 管道提供了一种机制:它在两个并发执行的协程之间进行同步,并通过传递与该管道元素类型相符的值来进行通信,它是Golang在语言层面提供的goroutine间的通信方式.通过Channel在不同的 goroutine中交换数据,在goroutine之间…...

CSS的浮动属性,web前端开发工程师
了解校招 知己知彼才能百战百胜,在准备校招之前,我们先要了解校招。 什么是校招? 校招,全称校园招聘,指企业招聘那些即将毕业的学生。校招主要分为三个部分:简历筛选,笔试,面试。 …...

Dubbo的集群容错方案
Dubbo提供了多种集群容错方案来保证分布式环境下的高可用性。这些容错方案可以在服务提供者不可用时,根据不同的业务需求和场景,选择不同的策略来处理。以下是Dubbo支持的一些主要集群容错方案: 1. Failover Cluster(失败自动切换…...
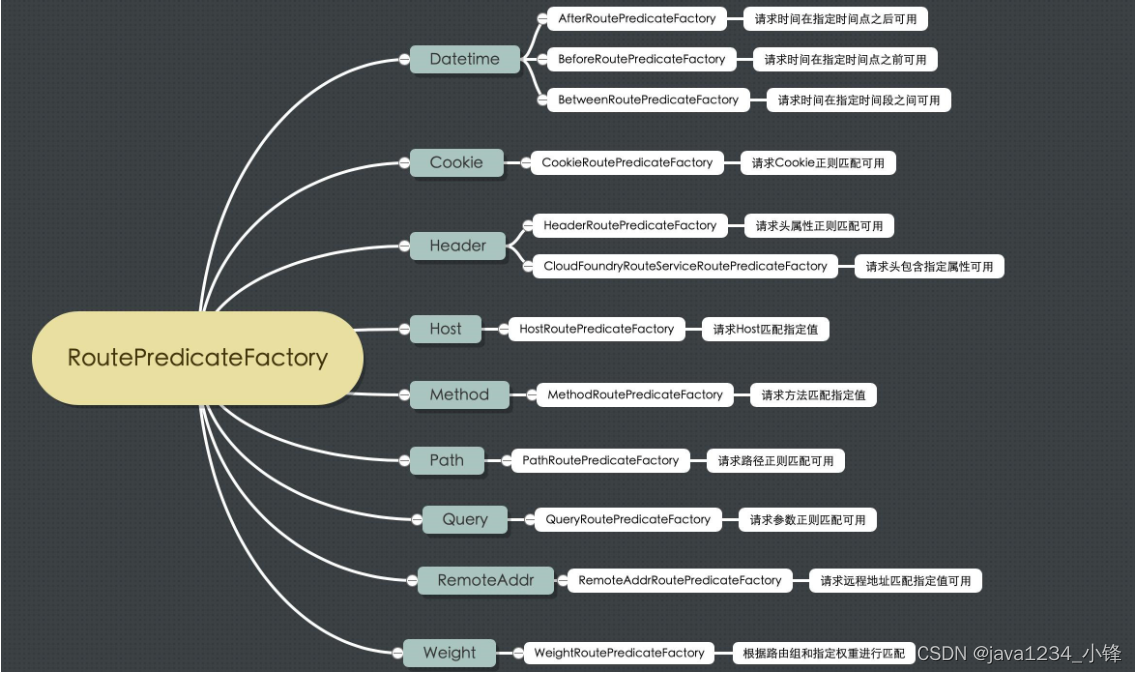
两天学会微服务网关Gateway-Gateway路由规则
锋哥原创的微服务网关Gateway视频教程: Gateway微服务网关视频教程(无废话版)_哔哩哔哩_bilibiliGateway微服务网关视频教程(无废话版)共计17条视频,包括:1_Gateway简介、2_Gateway工作原理、3…...
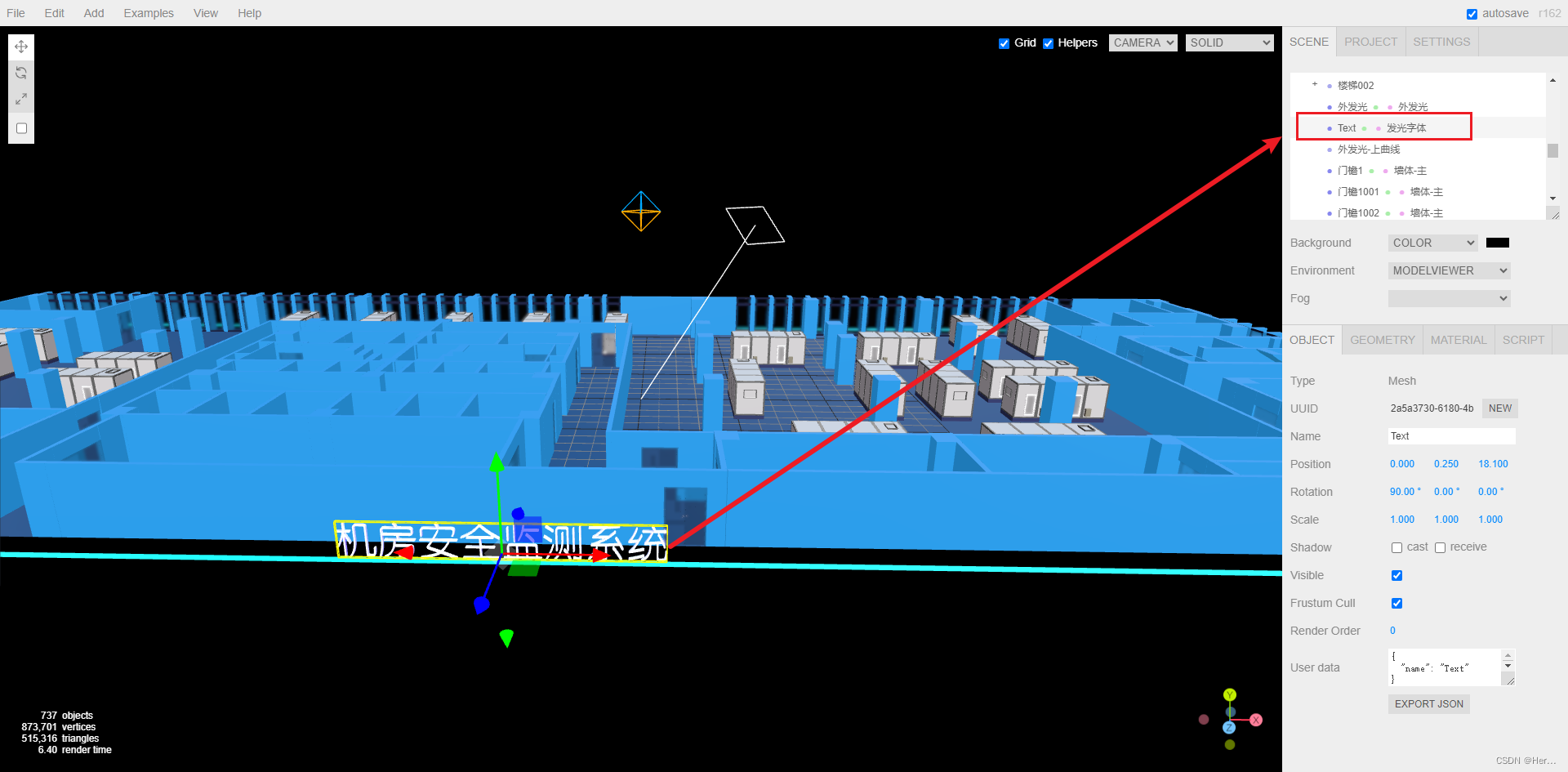
three.js如何实现简易3D机房?(一)基础准备-下
three.js如何实现简易3D机房?(一)基础准备-上:http://t.csdnimg.cn/MCrFZ 目录 四、按需引入 五、导入模型 四、按需引入 index.vue文件中 <template><div class"three-area"><div class"three-box" ref"threeDemoRef…...

Android高级工程师面试实战,三幅图给你弄懂EventBus核心原理
阿里技术一面-35min 自我介绍 Android 有没有遇到OOM问题(有遇到内存泄漏问题)Handler机制ThreadLocalActivity启动到加载View过程View绘制过程LinearLayout (wrap_content) & TextView (match_parent) 最终结果???OKHttp(1. 为什么选择它? 2. 性能了解不…...
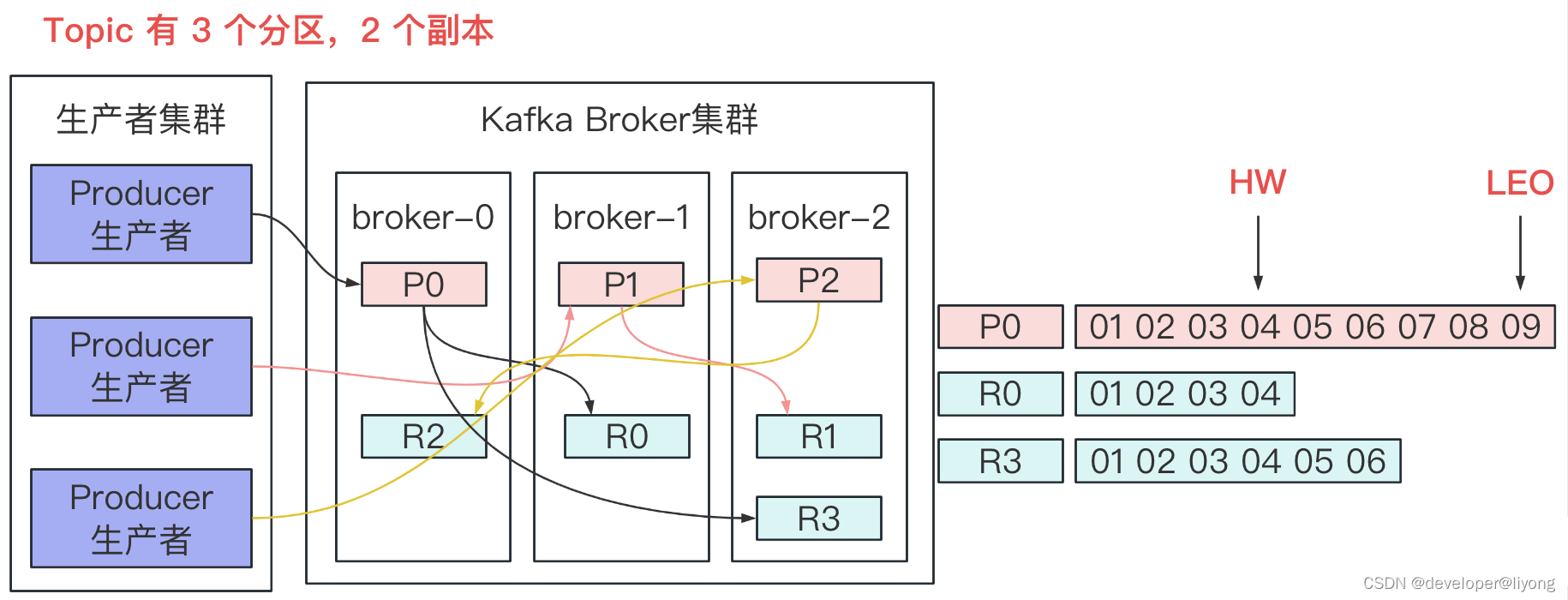
消息队列-kafka-服务端处理架构(架构,Topic文件结构,服务端数据的一致性)
服务端处理架构 资料来源于网络 网络线程池: 接受请求,num.network.threads,默认为 3,专门处理客户的发送的请求。 IO 线程池: num.io.threads,默认为 8,专门处理业务请求。也就是它不负责发…...
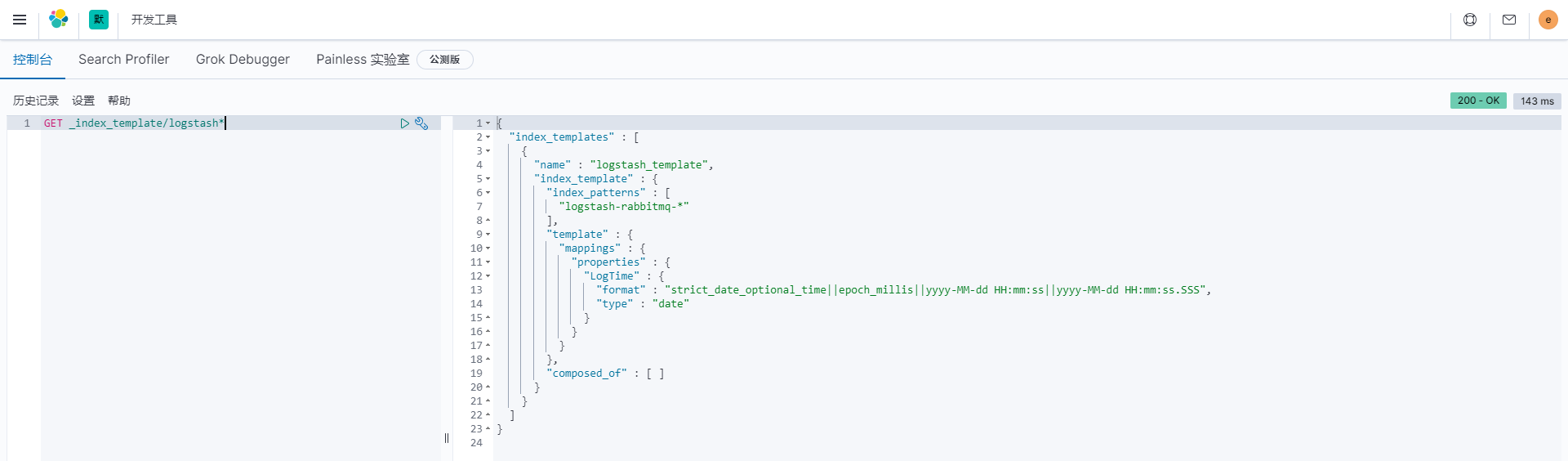
ES之API系列--index template(索引模板)的用法(有实例)
原文网址:ES之API系列--index template(索引模板)的用法(有实例)_IT利刃出鞘的博客-CSDN博客 简介 说明 本文介绍ElasticSearch的index template(索引模板)的用法(有实例)。 官网网址 https://www.elastic.co/guide/en/elasticsearch/reference/8.0/index-temp…...
electron+vue3全家桶+vite项目搭建【28】封装窗口工具类【2】窗口组,维护窗口关系
文章目录 引入实现效果思路主进程模块渲染进程模块测试效果 引入 demo项目地址 窗口工具类系列文章: 封装窗口工具类【1】雏形 封装窗口工具类【2】窗口组,维护窗口关系 封装窗口工具类【3】控制窗口定向移动 我们思考一下窗口间的关系,窗…...
docker安装ES和kibana
文章目录 一、安装Elasticsearch1. 安装Elasticsearch2. 安装IK分词器3. elasticsearch-head 监控的插件4. 配置跨域 二、安装kibana 提示:以下是本篇文章正文内容,下面案例可供参考 一、安装Elasticsearch 1. 安装Elasticsearch 安装Elasticsearch参…...
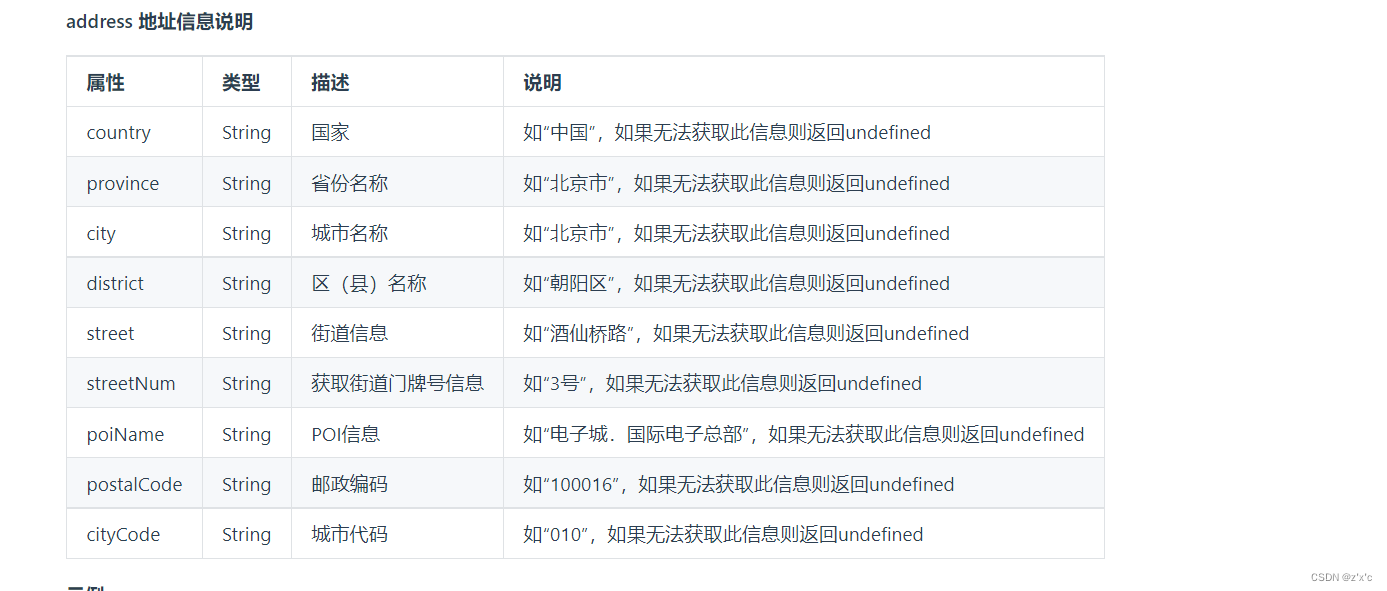
uniapp微信小程序获取当前位置
uni-app微信小程序uni.getLocation获取位置;authorize scope.userLocation需要在app.json中声明permission;小程序用户拒绝授权后重新授权-CSDN博客...
HarmonyOS创建项目和应用—设置数据处理位置
项目和应用介绍 关于项目 项目是资源、应用的组织实体。资源包括服务器、数据库、存储,以及您的应用、终端用户的数据等。在您使用部分服务时,您是数据的控制者,数据将按照您设置的数据处理位置来存储在指定区域。 通常,您不需…...
3.1_2024ctf青少年比赛部分web题
php后门 根据x-powered-by知道php的版本 该版本存在漏洞: PHP 8.1.0-dev 开发版本后门 根据报错信息,进行提示,前 GET / HTTP/1.1 Host: challenge.qsnctf.com:31639 User-Agentt:12345678system(cat /flag);var_dump(2*3);zerodium12345678…...

Vue3:OptionsAPI 与 CompositionAPI的比较
1、Vue2 Vue2的API设计是Options(配置)风格的。 Options API 的弊端 Options类型的 API,数据、方法、计算属性等,是分散在:data、methods、computed中的,若想新增或者修改一个需求,就需要分别…...

Rust! 无VDom! 尤雨溪解析 Vue.js 2024 新特性
视频号搜索“云前端”观看视频版 在 VueJS Amsterdam 2024 大会首日,Vue 创始人 Evan You 进行了开场主旨演讲。他首先回顾了 Vue 十年以来的累累硕果,指出 VueJS 从一个视图层工具,成功演化出全流程的社区生态。 Vue 3.4 谈到 Vue 3 的发展时…...
Windows上websocket客户端连接定时存储消息到文件并加载文件定时发送服务端工具实现
场景 在业务开发中,需要对接三方websocket协议数据或者连接并存储线上websocket协议数据,需要使用websocket客户端 连接线上的websocket服务端获取并存储数据,然后将数据存储成文件格式可移植,并将数据复制 到本地,…...
【STM32+OPENMV】二维云台颜色识别及追踪
一、准备工作 有关OPENMV最大色块追踪及与STM32通信内容,详情见【STM32HAL】与OpenMV通信 有关七针OLED屏显示内容,详情见【STM32HAL】七针OLED(SSD1306)配置(SPI版) 二、所用工具 1、芯片:STM32F407ZGT6 2、CUBEMX配置软件 3、KEIL5 4…...
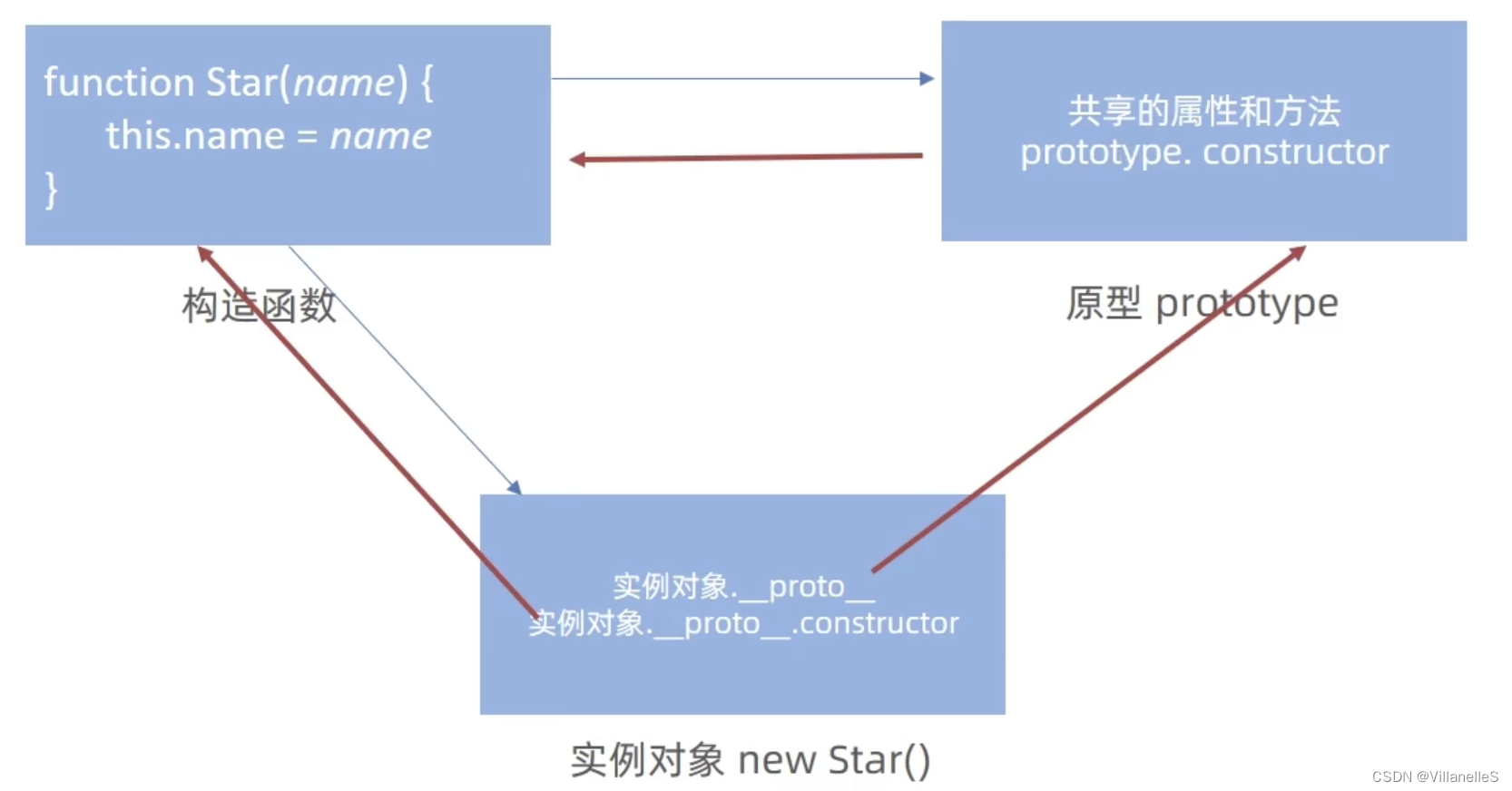
JavaScript基础3之面向对象关于面向过程、函数式编程、对比、构造函数、原型
JavaScript基础 面向对象面向过程函数式编程命令式编程函数式编程特性副作用透明引用不可变变量函数是一等公民 常见的函数式编程模型 面向对象为什么要使用面向对象封装继承多态 对比面向过程函数式编程面向对象 构造函数原型constructor使用场景 对象原型 面向对象 面向过程…...

运用Tensorflow进行目标检测
对象检测是一种计算机视觉技术,它使软件系统能够从给定的图像或视频中检测、定位并跟踪物体。对象检测的一个特殊属性是它能识别对象的类别(如人、桌子、椅子等)并在给定图像中指出其具体位置坐标。这个位置通常通过在物体周围绘制一个边界框…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...
