双重差分法(DID):算法策略效果评估的利器
文章目录
- 算法评估
- DID原理
- 简单实例
- Python实现
算法评估
作为一名算法出身的人,曾长期热衷于算法本身的设计和优化。至于算法的效果评估,通常使用公开数据集做测试,然后对比当前已公开的结果,便可得到结论。
但是在实际落地过程中,却遇到了问题:没有公开数据集;即便有,也依然有必要在实际场景下再做验证,毕竟公开数据集和实际场景往往都有很大区别。
理论上来说,新研发了一个算法后,需要和业务已经在使用的人工经验(被理解为一种特殊的策略)做对比;算法迭代后,前后两个版本的算法也需要做对比。
不失一般性,假设在某个区域内,评价指标为最大化JJJ,此前使用算法A,当前有了新算法B,该如何评估B相比A是否能更好地促进JJJ的提升呢?
理想情况下,是在该区域的两个平行时空中,一个使用算法A,另一个使用算法B,分别得到指标JAJ_AJA和JBJ_BJB。然后比较两个指标的优劣,如果JBJ_BJB指标更好,那么算法B可以被认为是更有利于指标JJJ的提升。
但在任意给定的时间点,该区域实际上只能处于一种状态,即只使用算法A或者只使用算法B,因此只能观察到JAJ_AJA或JBJ_BJB。
因此,需要寻找两个相同的区域,然后分别使用A算法和B算法,再基于得到的指标进行算法优劣的评估。当然,要找到两个相同的区域,在现实中是很困难的;但是如果区域不同,无论控制其多少个参数相同,都有可能让JJJ受到某些未观测参数的影响。
如果退而求其次,不要求完全相同,是否还有机会去科学地评估算法A和B呢?答案是有的,就是本文即将介绍的双重差分法(difference-in-differences,DID)。
DID原理
DID的原理如下图所示。选定两个区域1和2,以算法B的干预时刻为基准,将时间定义为干预前和干预后。在干预后,区域1保持不变,继续使用算法A,最终可以得到A增量;区域2使用算法B后,得到的B增量可以被拆解为两个部分:区域2的自然增量A’,以及算法B带来的纯增量B‘。A’可以理解为不使用算法B时区域2的增量。如果在干预前,两个区域针对指标JJJ的变化趋势保持一致,那么我们可以基于A和此前的变化趋势估计出A’,即做出反事实推断。由于区域2实际的增量B是已知的,因此算法B带来的纯增量为
B′=B−A′B'=B-A'B′=B−A′
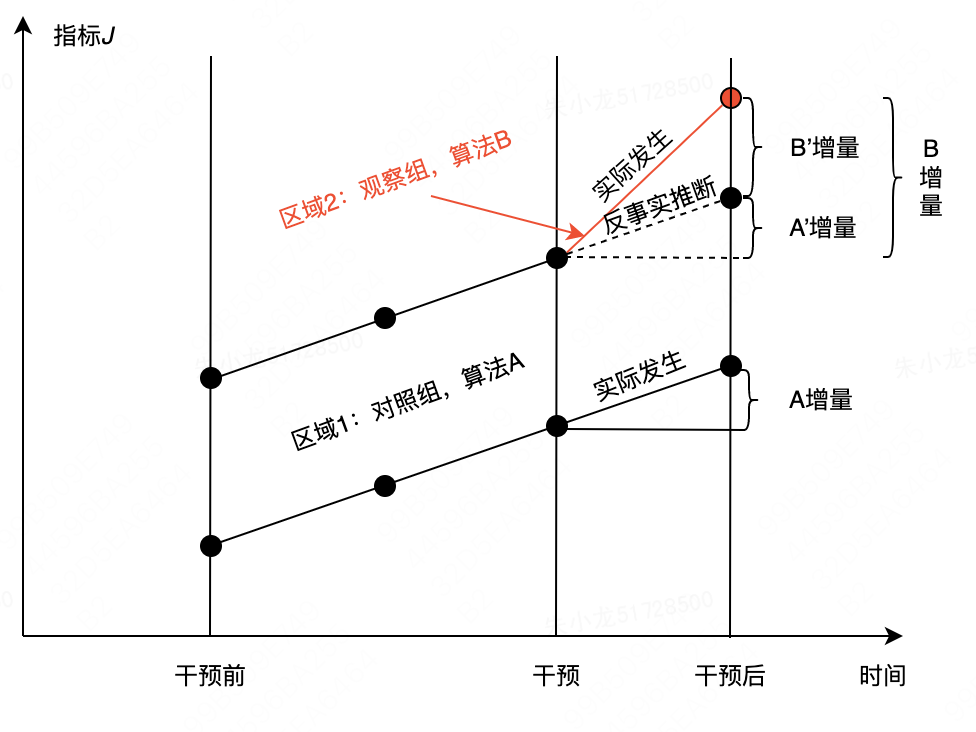
此时,我们发现,不再刻意要求区域1和区域2完全相同,只要求两者的历史指标变化区域保持一致即可,这显著降低了区域选取的难度。
如果使用数学表达式,可以描述为:
Yit=α+δDi+λTt+β(Di×Tt)+ϵitY_{it}=\alpha+\delta D_i+\lambda T_t+\beta(D_i \times T_t)+\epsilon_{it}Yit=α+δDi+λTt+β(Di×Tt)+ϵit
其中,YitY_{it}Yit为JJJ变量;α\alphaα为截距;δ\deltaδ、λ\lambdaλ和β\betaβ为系数值; DiD_iDi为算法B,干预前为0,干预后为1;TtT_tTt为时间,干预前为0,干预后为1;Di×TtD_i \times T_tDi×Tt为交叉项;ϵit\epsilon_{it}ϵit为随机项。
对上式取条件期望后,算法增量(上图中的B’)为β\betaβ,计算过程如下表所示。
| E(Y∣D,T)E(Y|D,T)E(Y∣D,T) | T=0T=0T=0 | T=1T=1T=1 | Δ\DeltaΔ |
|---|---|---|---|
| D=0D=0D=0 | α\alphaα | α+λ\alpha+\lambdaα+λ | λ\lambdaλ |
| D=1D=1D=1 | α+δ\alpha+\deltaα+δ | α+δ+λ+β\alpha+\delta+\lambda+\betaα+δ+λ+β | λ+β\lambda+\betaλ+β |
| Δ\DeltaΔ | δ\deltaδ | δ+β\delta+\betaδ+β | β\betaβ |
显然,如果β>0\beta>0β>0,则认为算法B对指标JJJ有正向促进作用;反之,则认为有负向抵制作用。
简单实例
那么,如何求解β\betaβ值呢?
目前大部分DID的代码都是基于stata实现的。因此,本节主要参考半块土豆切丝的视频,给出一个简单实例的计算过程。
实例描述为:A和B为历史指标的变化保持一致的两个地区,在1994年,B区实行了一项新政策,目标是评估新政策对指标yyy的影响。相关数据如下。
| country | year | y |
|---|---|---|
| A | 1990 | 1342787840 |
| A | 1991 | -1899660544 |
| A | 1992 | -11234363 |
| A | 1993 | 2645775360 |
| A | 1994 | 3008334848 |
| A | 1995 | 3229574144 |
| A | 1996 | 2756754176 |
| A | 1997 | 2771810560 |
| A | 1998 | 3397338880 |
| A | 1999 | 39770336 |
| B | 1990 | 1342787840 |
| B | 1991 | -1518985728 |
| B | 1992 | 1912769920 |
| B | 1993 | 1345690240 |
| B | 1994 | 2793515008 |
| B | 1995 | 1323696384 |
| B | 1996 | 254524176 |
| B | 1997 | 3297033216 |
| B | 1998 | 3011820800 |
| B | 1999 | 3296283392 |
此处先直接给出stata代码如下:
// stata代码gen period = (year>=1994) & !missing(year) // 生成时间虚拟变量D,1994年前为0,反之为1
gen treat = (country>1) & !missing(country) // 生成区域的虚拟变量T,干预为1,反之为0
gen did = period * treat // 生成交叉项D·Tdiff y, t(treat) p(period) // DID回归:diff方式
为了更好地理解上述代码,把基本公式再抄写一遍
Yit=α+δDi+λTt+β(Di×Tt)+ϵitY_{it}=\alpha+\delta D_i+\lambda T_t+\beta(D_i \times T_t)+\epsilon_{it}Yit=α+δDi+λTt+β(Di×Tt)+ϵit
对应到该实例:DDD是政策变量treat,B地区为1,A地区为0,上述第2行代码实现;TTT是时间变量period,1994-1999年为1,1990-1993年为0,第1行代码实现;Di×TtD_i \times T_tDi×Tt是交叉项did,第3行代码实现;β\betaβ的计算由第4行代码实现。
先看一下计算结果。
Number of observations in the DIFF-IN-DIFF: 20Before After Control: 4 6 10Treated: 4 6 108 12
--------------------------------------------------------Outcome var. | y | S. Err. | |t| | P>|t|
----------------+---------+---------+---------+---------
Before | | | | Control | 5.2e+08| | | Treated | 7.7e+08| | | Diff (T-C) | 2.5e+08| 1.0e+09| 0.24 | 0.811
After | | | | Control | 2.5e+09| | | Treated | 2.3e+09| | | Diff (T-C) | -2.0e+08| 8.4e+08| 0.24 | 0.812| | | |
Diff-in-Diff | -4.6e+08| 1.3e+09| 0.34 | 0.737
--------------------------------------------------------
R-square: 0.31
* Means and Standard Errors are estimated by linear regression
**Inference: *** p<0.01; ** p<0.05; * p<0.1输出内容看起来挺复杂,我们主要关注DIFF-in-Diff行、y列和P>|t|列的数值,分别是-4.6e8和0.737。其中-4.6e8即为我们要计算的β\betaβ值;0.737表征的是所得到β\betaβ值的靠谱程度,一般命名为ppp。该值如果小于0.05,表明β\betaβ值是有参考价值的;反之,无论β\betaβ值为多少,均认为无显著变化。所有情况罗列一遍:
| p>0.05p>0.05p>0.05 | p<0.05p<0.05p<0.05 | |
|---|---|---|
| β>0\beta>0β>0 | 无显著效果 | 显著正向效果 |
| β<0\beta<0β<0 | 无显著效果 | 显著负向效果 |
所以,在该实例中,可以得到结论:该新政策对指标y并没有显著效果。
Python实现
事实上,有了多组period、treat、did和y值之后,要计算β\betaβ,本质就是一个最小二乘法的优化问题。只不过此处,还需要求解ppp值。庆幸的是,该功能并不需要自己编写代码去实现,可以调用statsmodels工具包来求解。
以下为Python计算β\betaβ值的代码:
import statsmodels.formula.api as smf
import pandas as pdif __name__ == '__main__':df = pd.read_excel('test_data_101_1.xlsx')// 生成时间虚拟变量D,1994年前为0,反之为1df['period'] = df['year'].apply(lambda x: 1 if x >= 1994 else 0)// 生成区域的虚拟变量T,干预为1,反之为0df['treat'] = df['country'].apply(lambda x: 1 if x == 'B' else 0)// 生成交叉项D·Tdf['did'] = df['period'] * df['treat']// 调用smf计算beta值df = df[['period', 'treat', 'did', 'y']]model = smf.ols(formula='y ~ period + treat + did', data=df).fit()print(model.summary())
运行以上代码,可以得到
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.313
Model: OLS Adj. R-squared: 0.184
Method: Least Squares F-statistic: 2.430
Date: Sun, 05 Mar 2023 Prob (F-statistic): 0.103
Time: 22:27:31 Log-Likelihood: -448.21
No. Observations: 20 AIC: 904.4
Df Residuals: 16 BIC: 908.4
Df Model: 3
Covariance Type: nonrobust
==============================================================================coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 5.194e+08 7.31e+08 0.711 0.488 -1.03e+09 2.07e+09
period 2.015e+09 9.44e+08 2.135 0.049 1.42e+07 4.01e+09
treat 2.511e+08 1.03e+09 0.243 0.811 -1.94e+09 2.44e+09
did -4.556e+08 1.33e+09 -0.341 0.737 -3.28e+09 2.37e+09
==============================================================================
Omnibus: 2.990 Durbin-Watson: 2.288
Prob(Omnibus): 0.224 Jarque-Bera (JB): 2.423
Skew: -0.814 Prob(JB): 0.298
Kurtosis: 2.494 Cond. No. 7.66
==============================================================================
主要看did行、coef列和P>|t|列的数值。显然,该结果和stata的计算结果是完全一致的。
相关文章:

双重差分法(DID):算法策略效果评估的利器
文章目录算法评估DID原理简单实例Python实现算法评估 作为一名算法出身的人,曾长期热衷于算法本身的设计和优化。至于算法的效果评估,通常使用公开数据集做测试,然后对比当前已公开的结果,便可得到结论。 但是在实际落地过程中&…...

【pytorch】使用mixup技术扩充数据集进行训练
目录1.mixup技术简介2.pytorch实现代码,以图片分类为例1.mixup技术简介 mixup是一种数据增强技术,它可以通过将多组不同数据集的样本进行线性组合,生成新的样本,从而扩充数据集。mixup的核心原理是将两个不同的图片按照一定的比例…...

面向对象设计模式:创建型模式之单例模式
1. 单例模式,Singleton Pattern 1.1 Definition 定义 单例模式是确保类有且仅有一个实例的创建型模式,其提供了获取类唯一实例(全局指针)的方法。 单例模式类提供了一种访问其唯一的对象的方式,可以直接访问…...
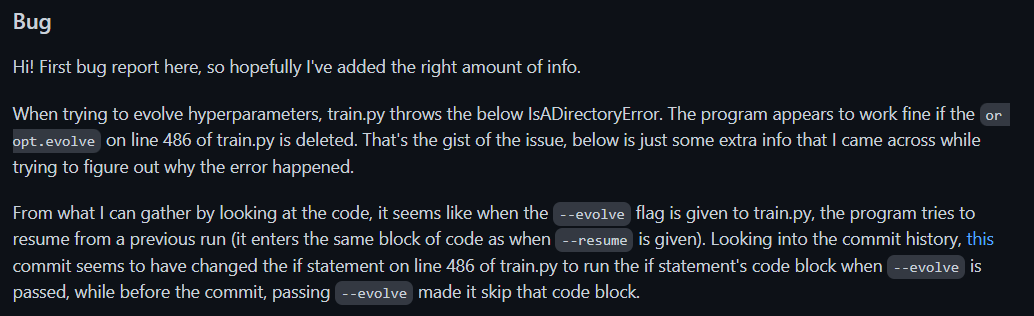
IsADirectoryError: [Errno 21] Is a directory: ‘.‘
项目场景: 基于YOLOv5的室内场景识别 工具:colab 问题描述 Traceback (most recent call last): File “train.py”, line 630, in main(opt) File “train.py”, line 494, in main d torch.load(last, map_location‘cpu’)[‘opt’] File “/usr/…...

判断三角面片与空间中球体是否相交
文章目录一、问题描述二、解题思路 在做项目时遇到了一个数学问题,即,如何判断给定一个三角面片与空间中某个球体有相交部分?这个问题看似简单,实际处理起来需要一些方法和手段。一、问题描述 已知空间中球体的球心位置center&a…...

继承下的缺省参数值和访问说明符
前言 本文将介绍 C 继承体系下,函数缺省参数的绑定和函数访问说明符的绑定。这些奇怪的问题实际上不应在我们的代码中出现,但它们能帮助我们理解 C 的动态绑定和静态绑定,也能帮助我们更好的通过面试。 缺省参数值 先来看一段代码…...
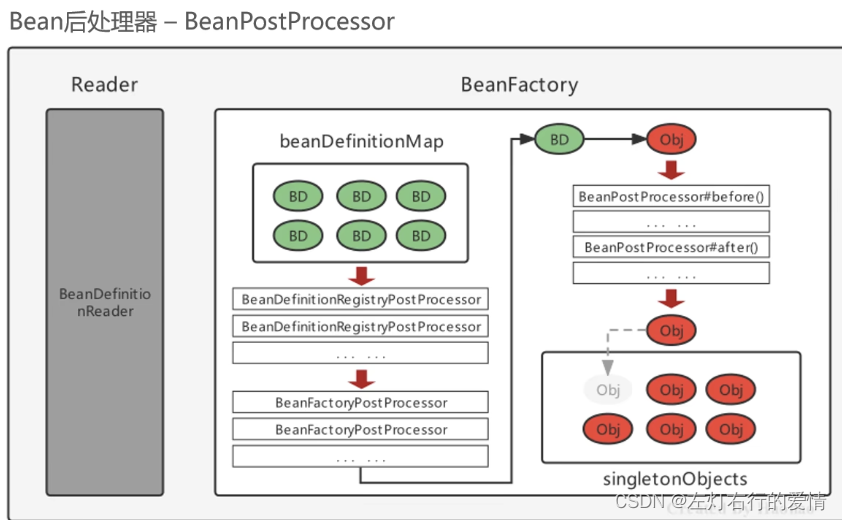
Spring核心模块—— BeanFactoryPostProcessorBeanPostProcessor(后处理器)
后置处理器前言Spring的后处理器BeanFactoryPostProcessor(工厂后处理器)执行节点作用基本信息经典场景子接口——BeanDefinitiRegistryPostProcessor基本介绍用途具体原理例子——注册BeanDefinition使用Spring的BeanFactoryPostProcessor扩展点完成自定…...
产品新人如何培养产品思维?
什么是产品思维?其实很难定义,不同人有不同的定义。有的人定义为以用户为中心打磨一个完美体验的产品;有的定义为从需求调研到需求上线各个步骤需要思考的点,等等。本文想讨论的产品思维是:怎么去发现问题,…...

「兔了个兔」CSS如此之美,看我如何实现可爱兔兔LOADING页面(万字详解附源码)
💂作者简介: THUNDER王,一名热爱财税和SAP ABAP编程以及热爱分享的博主。目前于江西师范大学会计学专业大二本科在读,同时任汉硕云(广东)科技有限公司ABAP开发顾问。在学习工作中,我通常使用偏后…...
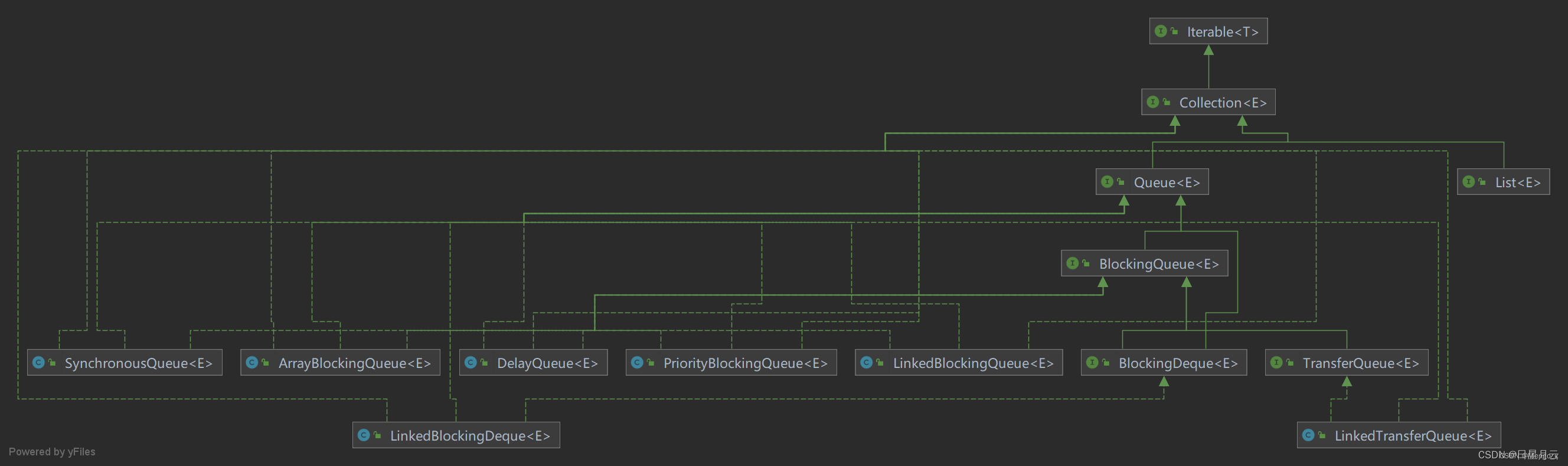
【Java】阻塞队列 BlcokingQueue 原理、与等待唤醒机制condition/await/singal的关系、多线程安全总结
在实习过程中使用阻塞队列对while sleep 轮询机制进行了改造,提升了发送接收的效率,这里做一点点总结。 自从Java 1.5之后,在java.util.concurrent包下提供了若干个阻塞队列,BlcokingQueue继承了Queue接口,是线程安全…...

【水下图像增强】Enhancing Underwater Imagery using Generative Adversarial Networks
原始题目Enhancing Underwater Imagery using Generative Adversarial Networks中文名称使用 GAN 增强水下图像发表时间2018年1月11日平台ICRA 2018来源University of Minnesota, Minneapolis MN文章链接https://arxiv.org/abs/1801.04011开源代码官方:https://gith…...

Maven专题总结—详细版
第一章 为什么使用Maven 获取jar包 使用Maven之前,自行在网络中下载jar包,效率较低。如【谷歌、百度、CSDN…】使用Maven之后,统一在一个地址下载资源jar包【阿里云镜像服务器等…】 添加jar包 使用Maven之前,将jar复制到项目工程…...
)
华为OD机试真题Java实现【字符串加密】真题+解题思路+代码(20222023)
字符串加密 题目 给你一串未加密的字符串str, 通过对字符串的每一个字母进行改变来实现加密, 加密方式是在每一个字母str[i]偏移特定数组元素a[i]的量, 数组a前三位已经赋值:a[0]=1,a[1]=2,a[2]=4。 当i>=3时,数组元素a[i]=a[i-1]+a[i-2]+a[i-3], 例如:原文 abcde …...

「Python 基础」函数与高阶函数
文章目录1. 函数调用函数定义函数函数的参数递归函数2. 高阶函数map/reducefiltersorted3. 函数式编程返回函数匿名函数装饰器偏函数1. 函数 函数是一种重复代码的抽象方式,Python 内建支持的一种封装; 调用函数 调用一个函数,需要知道函数…...

DIV内容滚动,文字符滚动标签marquee兼容稳定不卡
marquee(文字滚动)标签 marquee简介 <marquee>标签,是成对出现的标签,首标签<marquee>和尾标签</marquee>之间的内容就是滚动内容。 <marquee>标签的属性主要有behavior、bgcolor、direction、width、height、hspace、vspace、loop、scrollamount、scr…...
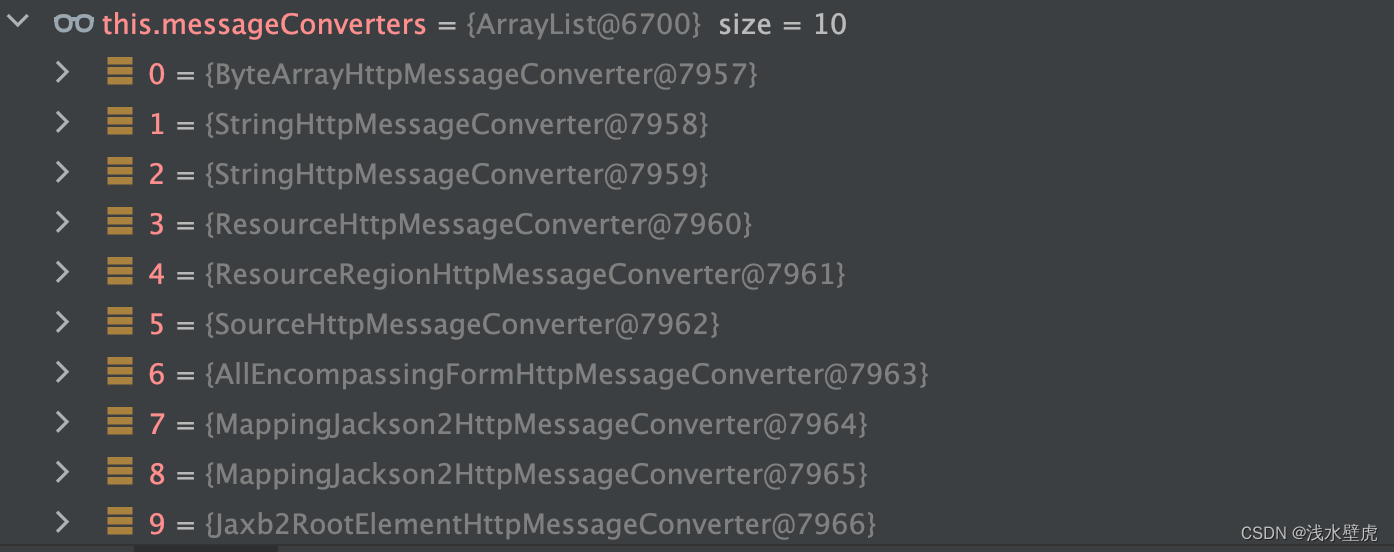
SpringBoot_第五章(Web和原理分析)
目录 1:静态资源 1.1:静态资源访问 1.2:静态资源源码解析-到WebMvcAutoConfiguration 2:Rest请求绑定(设置put和delete) 2.1:代码实例 2.2:源码分析到-WebMvcAutoConfiguratio…...

4-2 Linux进程和内存概念
文章目录前言进程状态进程优先级内存模型进程内存关系前言 进程是一个其中运行着一个或多个线程的地址空间和这些线程所需要的系统资源。一般来说,Linux系统会在进程之间共享程序代码和系统函数库,所以在任何时刻内存中都只有代码的一份拷贝。 进程状态…...

【微信小程序】计算器案例
🏆今日学习目标:第二十一期——计算器案例 ✨个人主页:颜颜yan_的个人主页 ⏰预计时间:30分钟 🎉专栏系列:我的第一个微信小程序 计算器前言实现效果实现步骤wxmlwxssjs数字按钮事件处理函数计算按钮处理事…...
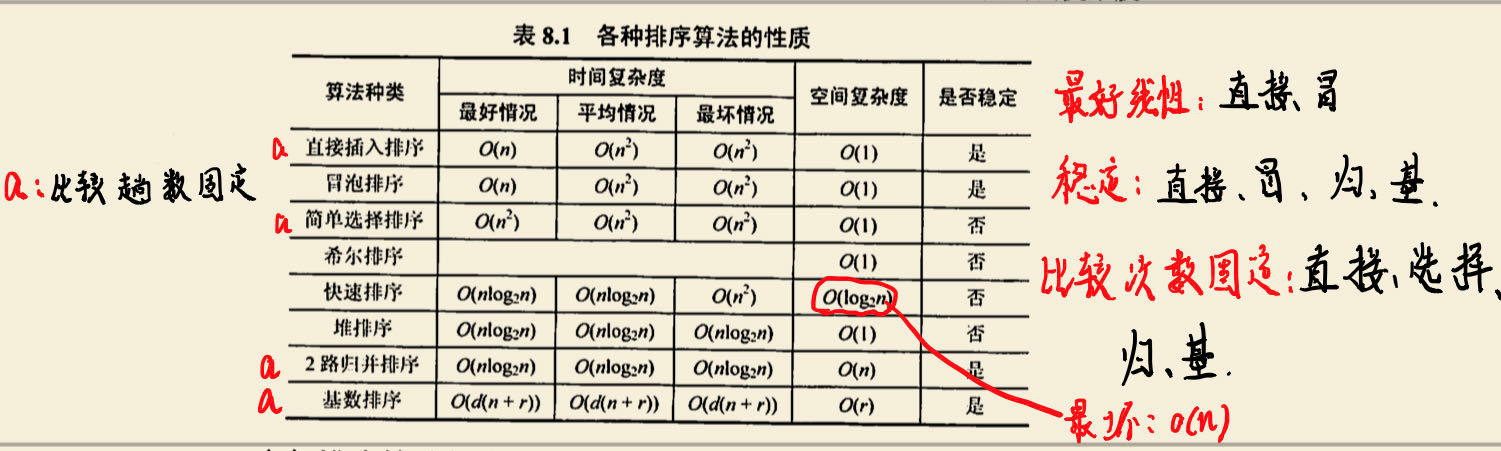
408 计算机基础复试笔记 —— 更新中
计算机组成原理 计算机系统概述 问题一、冯诺依曼机基本思想 存储程序:程序和数据都存储在同一个内存中,计算机可以根据指令集执行存储在内存中的程序。这使得程序具有高度灵活性和可重用性。指令流水线:将指令分成若干阶段,每…...
)
找出最大数-课后程序(Python程序开发案例教程-黑马程序员编著-第二章-课后作业)
实例6:找出最大数 “脑力大乱斗”休闲益智游戏的关卡中,有一个题目是找出最大数。本实例要求编写程序,实现从输入的任意三个数中找出最大数的功能。 实例分析 对于3个数比较大小,我们可以首先先对两个数的大小进行比较ÿ…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...
