代码随想录算法训练营Day52 | 300.最长递增子序列、674.最长连续递增序列、718.最长重复子数组
300.最长递增子序列
这题的重点是DP数组的定义,子序列必须以nums[i]为最后一个元素,这样dp数组中后面的元素才能与前面的元素进行对比
1、DP数组定义:dp[i]表示以nums[i]为最后一个元素的最长递增子序列长度
2、DP数组初始化:全部初始化为1(子序列最少也有自身一个)
3、递推公式:与 i 前所有元素进行对比,如果nums[i] > nums[j],那么更新dp[i]
· 基本——dp[j]:位置 j 处的最长递增子序列
· 新增—— +1:算上nums[i],多了一个递增元素
· 最后的递推公式:dp[i]取较大值:dp[i] = std::max(dp[i], dp[j] + 1)
4、遍历顺序:从前向后遍历
int lengthOfLIS(vector<int>& nums) {// dp[i]表示以nums[i]为最后一个元素的最长递增子序列长度// 全部初始化为1(子序列最少也有自身一个)vector<int> dp(nums.size(), 1);int ans = 1;for (int i = 1; i < nums.size(); ++i) {// 与i之前的所有元素做比较for (int j = 0; j < i; ++j) {// 不断更新dp[i],寻找以nums[i]为最后一个元素的最长递增子序列长度if (nums[i] > nums[j])dp[i] = std::max(dp[i], dp[j] + 1);}// 记录过程中的最长子序列if (dp[i] > ans)ans = dp[i];}return ans;
}674.最长连续递增序列
整体和上一题差不多,但由于要求是“连续”子序列,所以简单不少。主要差别在遍历过程中,为了保持序列连续,只需要与前一个元素对比即可(上一题需要与前面所有元素对比)。
int findLengthOfLCIS(vector<int>& nums) {vector<int> dp(nums.size(), 1);int ans = 1;for (int i = 1; i < nums.size(); ++i) {// 只需要与 i - 1 比较if (nums[i] > nums[i - 1]) {dp[i] = dp[i - 1] + 1;ans = std::max(ans, dp[i]);}}return ans;
}// 压缩空间写法
iint findLengthOfLCIS(vector<int>& nums) {int dp = 1;int ans = 1;for (int i = 1; i < nums.size(); ++i) {if (nums[i] > nums[i - 1])ans = std::max(ans, ++dp);elsedp = 1;}return ans;
}718.最长重复子数组
写暴力超时了,剪剪枝可能有机会过?
int findLength0(vector<int>& nums1, vector<int>& nums2) {// 尝试用哈希表来加快索引// key:值// value:出现值的下标unordered_map<int, vector<int>> mapNum2;for (int i = 0; i < nums2.size(); ++i) {auto it = mapNum2.find(nums2[i]);if (it == mapNum2.end())mapNum2.insert({ nums2[i], {i} });elseit->second.push_back(i);}vector<int> dp(nums1.size(), 0);int ans = 0;// 暴力两层循环 + 最内层判断重复子序列长度for (int i = 0; i < nums1.size(); ++i) {auto it = mapNum2.find(nums1[i]);if (it == mapNum2.end())continue;ans = std::max(ans, 1);for (int k : it->second) {int len = 1;for (int j = 1; i + j < nums1.size() && k + j < nums2.size(); ++j) {if (nums1[i + j] == nums2[k + j]) {dp[i + j] = std::max(dp[i + j], ++len);ans = std::max(ans, dp[i + j]);}elsebreak;}}}return ans;
}动规写法:
这题重点也是DP数组的定义:两个序列所以DP数组用二维
1、DP数组定义:两个维度表示两个数组的索引,dp[i][j]表示以nums1[i - 1]和nums2[j - 1]为结尾的两个字符串的最长重复子数组长度
(子序列问题一般都定义为 i - 1 和 j - 1,目的是精简初始化的步骤)
2、DP数组初始化:首行与首列元素无意义,但为了递推公式将其初始化为0,其余元素随意
3、递推公式:如果nums1[i - 1] == nums2[j - 1],那么dp[i][j] = dp[i - 1][j - 1] + 1
· 基本——dp[i - 1][j - 1]:以nums1[i - 2]和nums2[j - 1]为结尾的两个字符串的最长重复子数组长度
· 新增—— +1:加上新的这对匹配元素
· 最后的递推公式:dp[i] = std::max(dp[i], dp[j] + 1)
4、遍历顺序:从上到下从左到右遍历,先遍历nums1或nums2都可以
int findLength(vector<int>& nums1, vector<int>& nums2) {// dp[i][j]表示以nums1[i - 1]和nums2[j - 1]为结尾的两个字符串的最长重复子数组长度// 首行与首列元素无意义,为了递推公式将其初始化为0vector<vector<int>> dp(nums1.size() + 1, vector<int>(nums2.size() + 1, 0));int ans = 0;for (int i = 1; i <= nums1.size(); ++i) {for (int j = 1; j <= nums2.size(); ++j) {if (nums1[i - 1] == nums2[j - 1]) {// dp[i][j]的值由dp[i - 1][j - 1]递推得到dp[i][j] = dp[i - 1][j - 1] + 1;ans = std::max(ans, dp[i][j]);}}}return ans;
}相关文章:

代码随想录算法训练营Day52 | 300.最长递增子序列、674.最长连续递增序列、718.最长重复子数组
300.最长递增子序列 这题的重点是DP数组的定义,子序列必须以nums[i]为最后一个元素,这样dp数组中后面的元素才能与前面的元素进行对比 1、DP数组定义:dp[i]表示以nums[i]为最后一个元素的最长递增子序列长度 2、DP数组初始化:全部…...

一个测试OOM killer的程序未触发OOM所带来的问题
概述 我们知道,由于MMU实现了虚拟地址到物理地址的转换,所以我们在申请虚拟地址时往往可以申请一大块内存,这实际上是对资源的有效利用,毕竟只有内存真正被投入使用时(如memset)才会实际分配物理内存&…...

SanctuaryAI推出Phoenix: 专为工作而设计的人形通用机器人
文章目录 1. Company2. Main2.1 关于凤凰™ (Phoenix)2.2 关于碳™(Carbon)2.3 商业化部署2.4 关于 Sanctuary Corporation 3. My thoughtsReference彩蛋:将手机变为桌面小机器人 唯一入选《时代》杂志 2023 年最佳发明的通用机器人。 称机器人自主做家务的速度和灵…...
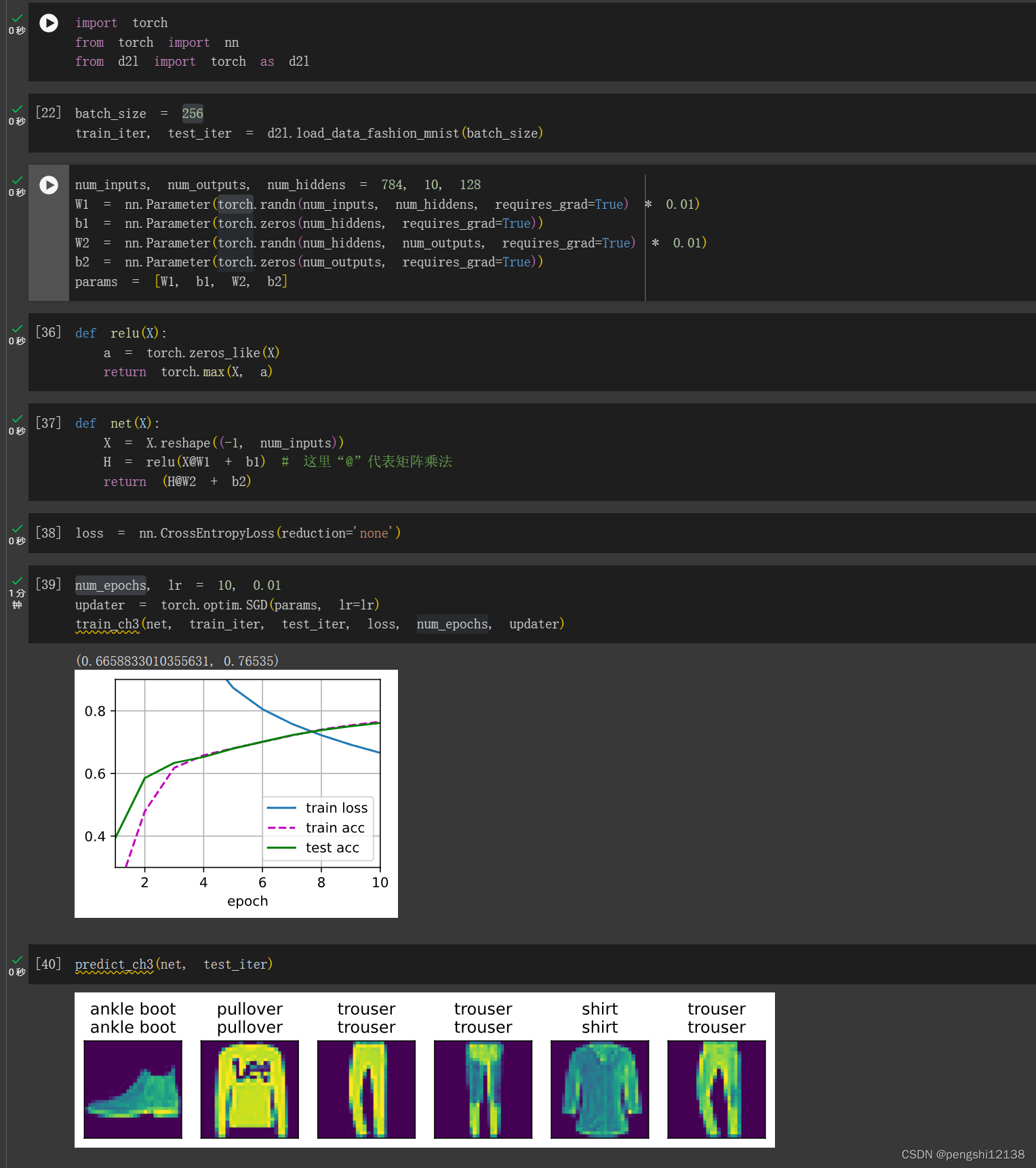
李沐动手学习深度学习——4.2练习
1. 在所有其他参数保持不变的情况下,更改超参数num_hiddens的值,并查看此超参数的变化对结果有何影响。确定此超参数的最佳值。 通过改变隐藏层的数量,导致就是函数拟合复杂度下降,隐藏层过多可能导致过拟合,而过少导…...

CYQ.Data 支持 DaMeng 达梦数据库
DaMeng 达梦数据库介绍: 达梦数据库(DMDB)是中国自主研发的关系型数据库管理系统,由达梦科技股份有限公司开发。 达梦数据库提供了企业级的数据库解决方案,广泛应用于金融、电信、政府、制造等行业领域。 达梦数据库具有以下特点和优势: 高性能:具备高性能的并发处理…...
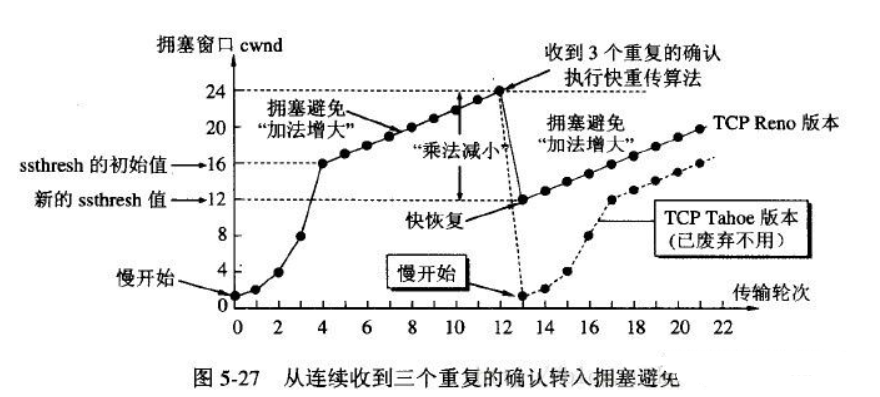
计网面试题整理上
1. 计算机网络的各层协议及作用? 计算机网络体系可以大致分为一下三种,OSI七层模型、TCP/IP四层模型和五层模型。 OSI七层模型:大而全,但是比较复杂、而且是先有了理论模型,没有实际应用。TCP/IP四层模型:…...
code: 500 ] This subject is anonymous - it does not have any identifying
项目场景: 相关背景: 使用idea 开发java 项目,前端页面请求 页面中相关的接口时,idea 控制台有报错信息出现,前端请求失败。 问题描述 问题: 使用idea 开发java 项目,前端页面请求 页面中相…...
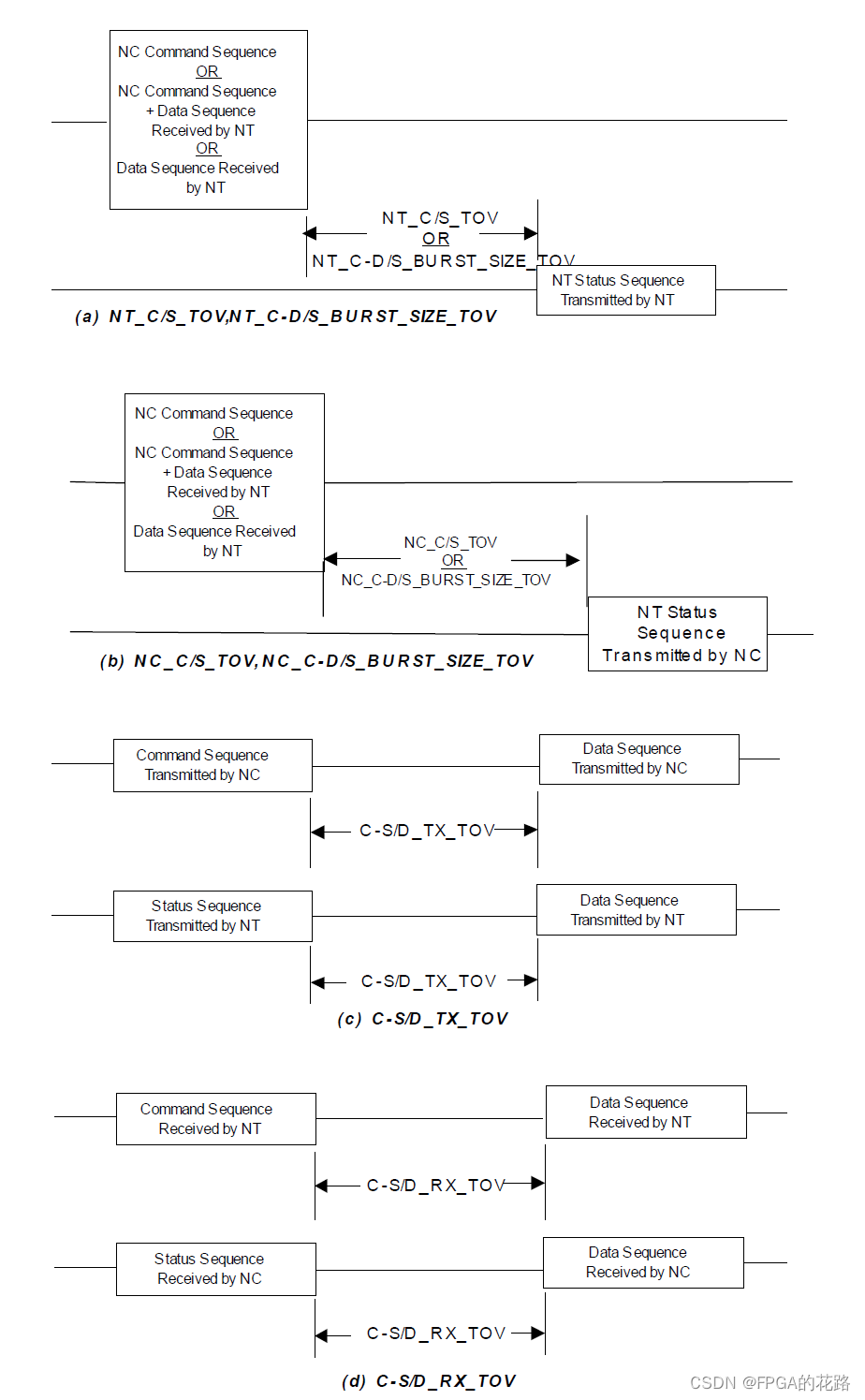
FC-AE-1553 协议
FC-AE-1553 协议 MIL-STD-1553B总线协议总线结构字格式消息传输方式 FC协议FC协议栈拓扑结构服务类型帧/序列/交换FC帧格式 FC-AE-1553网络构成帧类型命令帧状态帧数据帧 Information UnitsNC1NC2NC3-4NC5-7NT1-7 传输模式1. NC-NT2. NT-NC3. NT-NT4. 无数据字的模式命令5. 带数…...

代码随想录算法训练营day38|理论基础、509. 斐波那契数、70. 爬楼梯、746. 使用最小花费爬楼梯
理论基础 代码随想录 视频:从此再也不怕动态规划了,动态规划解题方法论大曝光 !| 理论基础 |力扣刷题总结| 动态规划入门_哔哩哔哩_bilibili 动态规划:如果某一问题有很多重叠子问题,使用动态规划是最有效的。所以动态…...

夫妻一方名下股权到底归谁?
生效判决摘要:1.夫妻一方在婚姻关系存续期间投资的收益,为夫妻的共同财产,归夫妻共同所有,但是并不能据此否定股权本身可能成为夫妻共同财产。婚姻关系存续期间登记在配偶一方名下的股权能否成为夫妻共同财产,可由司法…...
git根据文件改动将文件自动添加到缓冲区
你需要修改以下脚本中的 use_cca: false 部分 #!/bin/bash# 获取所有已修改但未暂存的文件 files$(git diff --name-only)for file in $files; do# 检查文件中是否存在"use_cca: false"if grep -q "use_cca: false" "$file"; thenecho "Ad…...

SystemVerilog Constants、Processes
SystemVerilog提供了三种类型的精化时间常数: •参数:与最初的Verilog标准相同,可以以相同的方式使用。 •localparameter:与参数类似,但不能被上层覆盖模块。 •specparam:用于指定延迟和定时值&#x…...

交易平台开发:构建安全/高效/用户友好的在线交易生态圈
在数字化浪潮的推动下,农产品现货大宗商品撮合交易平台已成为连接全球买家与卖家的核心枢纽。随着电子商务的飞速发展,一个安全、高效、用户友好的交易平台对于促进交易、提升用户体验和增加用户黏性至关重要。本文将深入探讨交易平台开发的关键要素&…...

Linux系统之部署复古游戏平台
Linux系统之部署复古游戏平台 前言一、项目介绍1.1 项目简介1.2 项目特点1.3 游戏平台介绍二、本次实践介绍二、本地环境介绍2.1 本地环境规划2.2 本次实践介绍三、本地环境检查3.1 安装Docker环境3.2 检查Docker服务状态3.3 检查Docker版本3.4 检查docker compose 版本四、构建…...

开源计算机视觉库opencv-python详解
开源计算机视觉库opencv-python详解 OpenCV-Python的核心功能:安装OpenCV-Python:使用OpenCV-Python的基本步骤:OpenCV-Python的高级应用:注意事项:OpenCV-Python的高级应用示例:1. 人脸识别2. 目标跟踪3. …...

Vue开发实例(十)Tabs标签页打开、关闭与路由之间的关系
创建标签页 一、创建标签页二、点击菜单展示新标签页1、将标签数据作为全局使用2、菜单点击增加标签页3、处理重复标签4、关闭标签页 三、点击标签页操作问题1:点击标签页选中菜单进行高亮展示问题2:点击标签页路由也要跳转 四、解决bug 先展示最终效果 …...

基于51单片机的智能火灾报警系统
基于51单片机的智能火灾报警系统 摘要: 本文提出了一种基于51单片机的智能火灾报警系统。该系统采用烟雾传感器和温度传感器来检测火灾的发生,并通过单片机进行数据处理和报警控制。此外,该系统还具有无线通信功能,可以实时将火灾…...

【数据结构】堆的TopK问题
大家好,我是苏貝,本篇博客带大家了解堆的TopK问题,如果你觉得我写的还不错的话,可以给我一个赞👍吗,感谢❤️ 目录 一. 前言二. TopK三. 代码 一. 前言 TOP-K问题:即求数据结合中前K个最大的元…...

Vue后台管理系统笔记-01
npm(Node Package Manager)和 yarn 是两个常用的包管理工具,用于在 Node.js 项目中安装、管理和更新依赖项。它们有以下几个区别: 性能和速度:在包的安装和下载方面,yarn 通常比 npm 更快速。yarn 使用了并…...
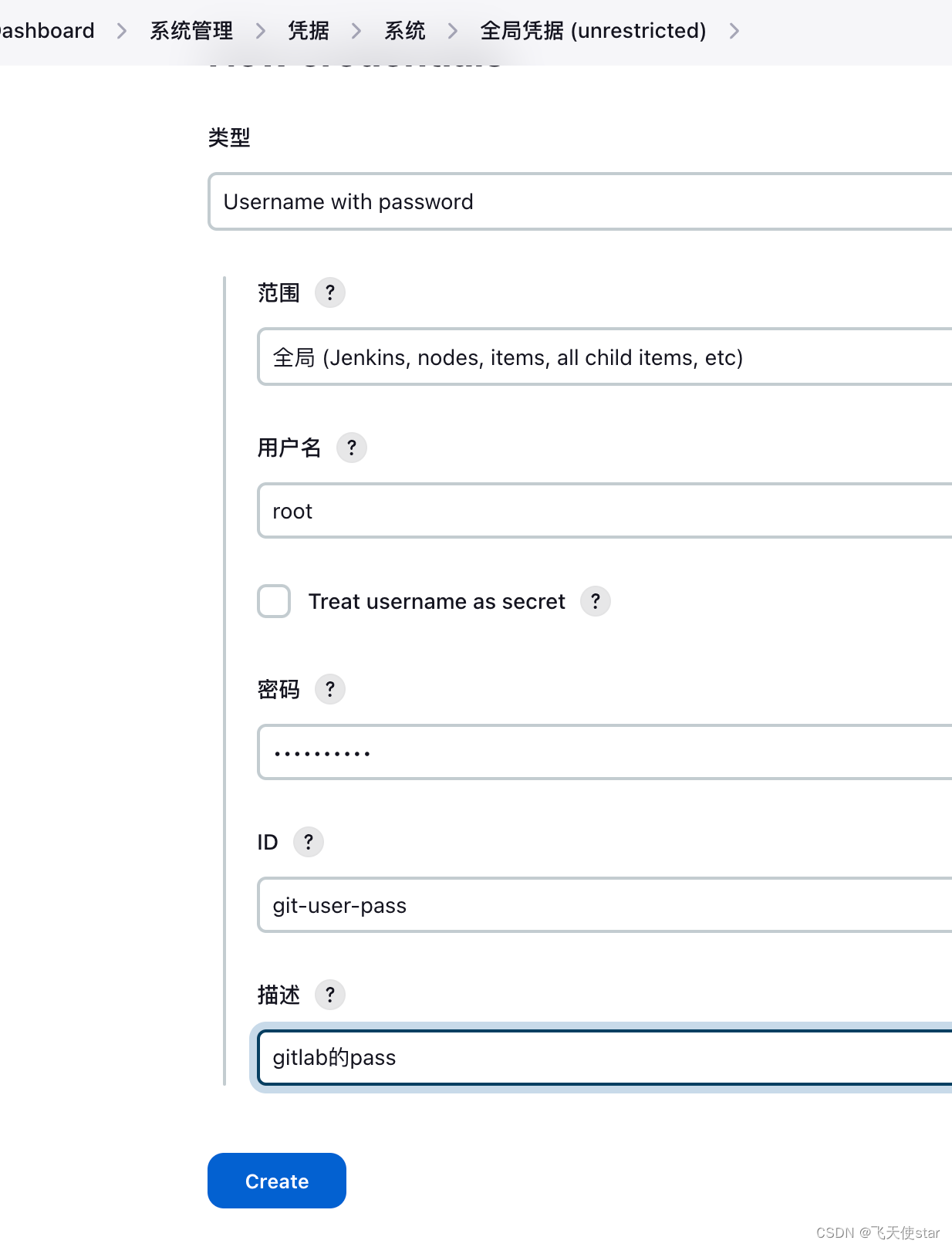
飞天使-学以致用-devops知识点3-安装jenkins
文章目录 构建带maven环境的jenkins 镜像安装jenkinsjenkins yaml 文件安装插件jenkins 配置k8s创建用户凭证 构建带maven环境的jenkins 镜像 # 构建带 maven 环境的 jenkins 镜像 docker build -t 192.168.113.122:8858/library/jenkins-maven:jdk-11 .# 登录 harbor docker …...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...
