算法练习-二分查找(一)
算法练习-二分查找
1 代码实现
1.1 非递归实现
public int bsearch(int[] a, int n, int value) {int low = 0;int high = n - 1;while (low <= high) {int mid = (low + high) / 2;if (a[mid] == value) {return mid;} else if (a[mid] < value) {low = mid + 1} else {high = mid - 1;}}return -1;
}
1.2 递归实现
public int bsearch_r(int[] a, int n, int value) {return bsearch(a, 0, n - 1, value);
}public int bsearch(int[] a, int low, int high, int value) {if (low > high) return -1;int mid = (low + high) / 2;if (a[mid] == value) {return mid;} else if (a[mid] < value) {return bsearch(a, mid + 1, high, value);} else {return bsearch(a, low, mid - 1, value);}
}
2 解题技巧
二分查找的正确姿势:
- 查找区间永远是闭区间[low, high]
- 循环条件永远是:low < high
- 对于low == high的情况,必要的时候特殊处理,在while内部补充退出条件
- 返回值永远是mid,不是low、high
- low、high的更新永远是low = mid + 1 和 high = mid - 1
- 对于非确定性查找,使用前后探测法来确定搜索区间
- 先处理命中目标,再处理左右半部分查找的情况
3 查找第一个等于x、最后一个等于x的元素
3.1 查找第一个等于x的元素
public int bsearch(int[] a, int n, int target) {int low = 0;int high = n - 1;while (low <= high) {int mid = low + (high - low) / 2;if (a[mid] == target) {if ((mid == 0) || (a[mid - 1] != target)) return mid;else high = mid - 1;} else if (a[mid] > target) {high = mid - 1;} else {low = mid + 1;}}return -1;
}
3.2 查找最后一个等于x的元素
public int bsearch(int[] a, int n, int target) {int low = 0;int high = n - 1;while (low <= high) {int mid = low + (high - low) / 2;if (a[mid] == target) {if ((mid == n - 1) || (a[mid + 1] != target)) return mid;else low = mid + 1;} else if (a[mid] > target) {high = mid - 1;} else {low = mid + 1;}}return -1;
}
4 查找第一个大于等于x,最后一个小于等于x的数
4.1 查找第一个大于等于x的数
public int bsearch(int[] a, int n, int target) {int low = 0;int high = n - 1;while (low <= high) {int mid = low + (high - low) / 2;if (a[mid] >= target) {if ((mid == 0) || (a[mid - 1] < target)) return mid;else high = mid - 1;} else {low = mid + 1;}}return -1;
}
4.2 查找最后一个小于等于x的数
public int bsearch(int[] a, int n, int target) {int low = 0;int high = n - 1;while (low <= high) {int mid = low + (high - low) / 2;if ((mid == n - 1) || (a[mid + 1] > target)) return mid;else low = mid + 1;} else {high = mid - 1;}
}
return -1;
}
5 循环有序数组中查找元素x
public int bsearch(int[] a, int n, int target) {int low = 0;int high = n - 1;while (low <= high) {int mid = low + (high - low) / 2;if (a[mid] == target) return mid;else if (a[low] <= a[mid]) {if (target >= a[low] && target < a[mid]) {high = mid - 1;} else {low = mid + 1;}} else {if (target > a[mid] && target <= a[high]) {low = mid + 1;} else {high = mid - 1;}}}return -1;
}
6 循环有序数组查找最小值
public int bsearch(int[] a, int n) {int low = 0;int high = n - 1;while (low <= high) {int mid = (low + high) / 2;if (low == high) return mid;if ((mid != 0 && a[mid] < a[mid - 1]) || (mid == 0 && a[mid] < a[high]) {return mid;} else if (a[mid] > a[high]) {low = mid + 1;} else {high = mid - 1;}}return -1;
}
7 查找峰值
链接:https://leetcode.cn/problems/find-peak-element
7.1 题目
峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。
你必须实现时间复杂度为 O(log n) 的算法来解决此问题。
示例 1:
输入:nums = [1,2,3,1]
输出:2
解释:3 是峰值元素,你的函数应该返回其索引 2。
示例 2:
输入:nums = [1,2,1,3,5,6,4]
输出:1 或 5
解释:你的函数可以返回索引 1,其峰值元素为 2;
或者返回索引 5, 其峰值元素为 6。
提示:
1 <= nums.length <= 1000
-231 <= nums[i] <= 231 - 1
对于所有有效的 i 都有 nums[i] != nums[i + 1]
7.2 题解
class Solution {public int findPeakElement(int[] nums) {int n = nums.length;int low = 0;int high = n - 1;while (low <= high) {int mid = (high + low) / 2;if (mid == 0) {if (n == 1) return 0;else if (nums[mid] > nums[mid + 1]) return mid;else low = mid + 1;} else if (mid == n - 1) {if (nums[mid] > nums[mid - 1]) return mid;else high = mid - 1;} else if (nums[mid] > nums[mid + 1] && nums[mid] > nums[mid - 1]) {return mid;} else if (nums[mid] > nums[mid - 1]) {low = mid + 1;} else {high = mid - 1;}}return 0;}
}
8 x的平方根
链接:https://leetcode.cn/problems/sqrtx
8.1 题目
给你一个非负整数 x ,计算并返回 x 的 算术平方根 。
由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。
注意:不允许使用任何内置指数函数和算符,例如 pow(x, 0.5) 或者 x ** 0.5 。
示例 1:
输入:x = 4
输出:2
示例 2:
输入:x = 8
输出:2
解释:8 的算术平方根是 2.82842…, 由于返回类型是整数,小数部分将被舍去。
8.2 题解
class Solution {public int mySqrt(int x) {if (x == 0) return 0;int low = 1;int high = x / 2 + 1;while (low <= high) {int mid = low + (high - low) / 2;long mid2 = (long)mid * mid;if (mid2 <= x) {long mid22 = ((long)mid + 1) * (mid + 1);if (mid22 <= x) {low = mid + 1;} else {return mid;}} else {high = mid - 1; }}return -1;}
}
相关文章:
)
算法练习-二分查找(一)
算法练习-二分查找 1 代码实现 1.1 非递归实现 public int bsearch(int[] a, int n, int value) {int low 0;int high n - 1;while (low < high) {int mid (low high) / 2;if (a[mid] value) {return mid;} else if (a[mid] < value) {low mid 1} else {high …...
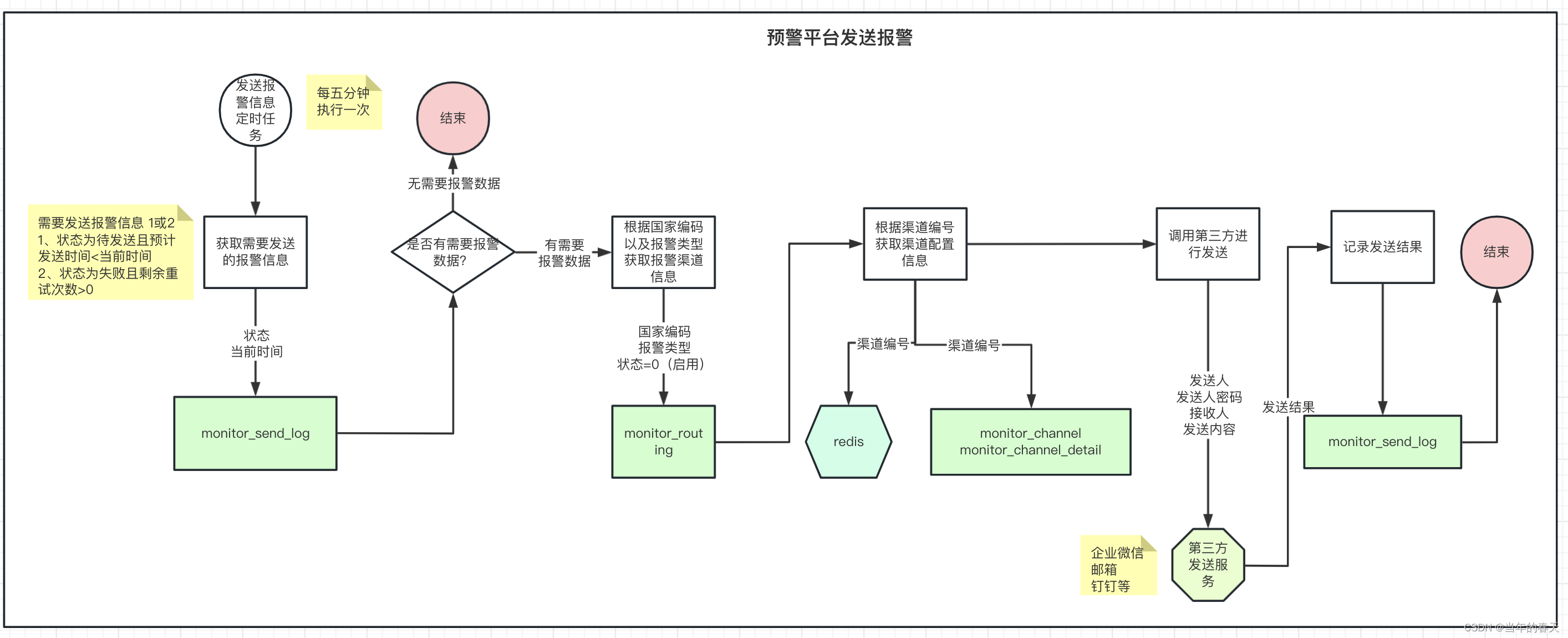
通用业务平台设计(五):预警平台建设
前言 在上家公司,随着业务的不断拓展(从支持单个国家单个主体演变成支持多个国家多个主体),对预警的诉求越来越紧迫;如何保障业务的稳定性那?预警可以帮我们提前甄别风险,从而让我们可以在风险来临前将其消灭ÿ…...

Windows openssl-1.1.1d vs2017编译
工具: 1. perl(https://strawberryperl.com/) 2. nasm(https://nasm.us/) 3. openssl源码(https://www.openssl.org/) 可以自己去下载 或者我的网盘提供下载: 链接:…...

【深蓝学院】手写VIO第2章--IMU传感器--笔记
0. 内容 1. 旋转运动学 角速度的推导: 左ω∧\omega^{\wedge}ω∧,而ω\omegaω是在z轴方向运动,θ′[0,0,1]T\theta^{\prime}[0,0,1]^Tθ′[0,0,1]T 两边取模后得到结论: 线速度大小半径 * 角速度大小 其中,对旋转矩…...
网络基础(二)之HTTP与HTTPS
应用层 再谈 "协议" 协议是一种 "约定". socket api的接口, 在读写数据时, 都是按 "字符串" 的方式来发送接收的. 如果我们要传输一些"结构化的数据" 怎么办呢? 为什么要转换呢? 如果我们将struct message里面的信息…...

Python每日一练(20230306)
目录 1. 翻转二叉树 ★★ 2. 最长公共前缀 ★★ 3. 2的幂 ★ 1. 翻转二叉树 翻转一棵二叉树。 示例 1: 输入: 4/ \2 7/ \ / \ 1 3 6 9 输出: 4/ \7 2/ \ / \ 9 6 3 1示例 2: 输入: 1…...

C/C++每日一练(20230305)
目录 1. 整数分解 ☆ 2. 二叉树的最小深度 ★★ 3. 找x ★★ 1. 整数分解 输入一个正整数,将其按7进制位分解为各乘式的累加和。 示例 1: 输入:49 输出:497^2示例 2: 输入:720 输出:720…...

SAS字典的应用
数据字典中常用信息检索DICTIONARY.COLUMNS、DICTIONARY.TABLES以及DICTIONARY.MEMBERS等字典表的内容。在编程实践中,如何以SAS字典表来提高效率。 1、DICTIONARY.COLUMNS 对于当前SAS任务的全部数据集,表格DICTIONARY.COLUMNS包含了诸如变量的名称、类…...

Mysql中的函数和触发器
函数函数是什么?多用于查询语句,实现了某种功能;用途与存储过程不同,但语法是类似的;函数语法create function 函数名([参数列表]) returns 数据类型 begin DECLARE 变量; sql 语句; return 值; end; 设置函…...

分布式架构之(Zookeeper原理)
Zookeeper是一个典型的分布式数据一致性的结局方案,分布式应用程序可以基于它实现注入数据发布、订阅、负载均衡、命名服务、分布式协调/通知、集群管理、Master选举、分布式锁和分布式队列等功能, Zookeeper可以保证如下分布式一致性特性: 顺…...

Java框架学习 | MyBatis
问题导向学习MyBatis 为什么要有MyBatis框架? 避免Java开发者直接使用 JDBC重复做数据库操作,同时更便捷地实现想要的数据库相关功能,让Java专注于开发业务。 MyBatis框架如何实现该目的? MyBatis是半自动化持久层ORM框架&#x…...
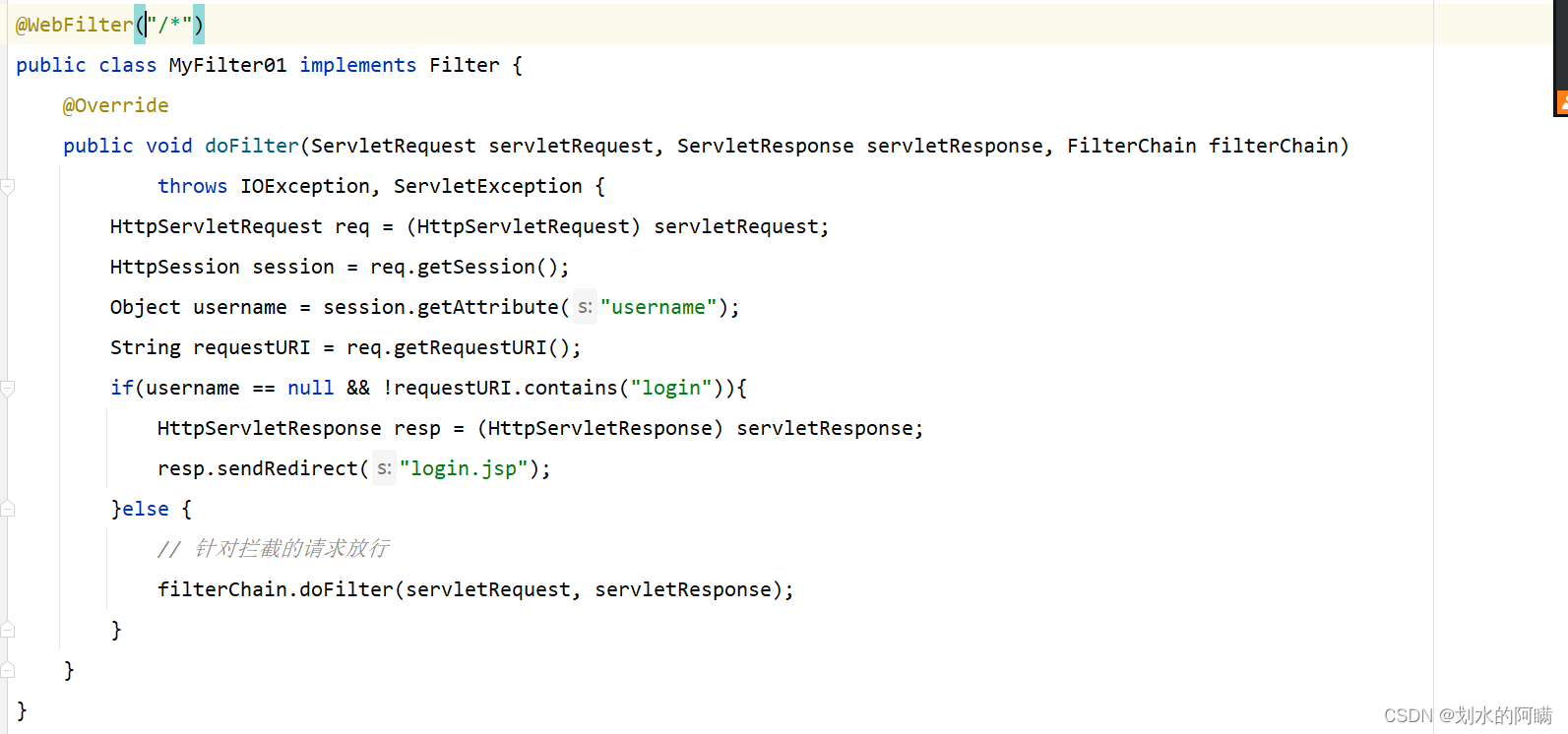
Cookie+Session详解
文章目录批量删除会话技术简介CookieCookie 查看Cookie 的删除Cookie 使用页面获取 cookie 信息cookie 特点Sessionsession 的使用Session 登录权限验证过滤器简介过滤器的使用WebFilter 注解过滤放行登录权限验证批量删除 servlet 类 dao 层 会话技术 简介 在计算机领域…...

CAPL脚本要注意区分elcount和strlen求数组长度的区别,不然要吃大亏
🍅 我是蚂蚁小兵,专注于车载诊断领域,尤其擅长于对CANoe工具的使用🍅 寻找组织 ,答疑解惑,摸鱼聊天,博客源码,点击加入👉【相亲相爱一家人】🍅 玩转CANoe&…...

CSS常用选择器
目录 1.CSS是什么 2.CSS的三种写法 2.1内部样式 2.2内联样式 2.3外部样式 3.CSS选择器 3.1标签选择器 3.2类选择器(更好的选择) 3.3ID选择器 3.4后代选择器 3.5子选择器 3.6并集选择器 3.7伪类选择器(复合选择器的特殊用法) 1.CSS是什么 CSS全称Cascding Style Sh…...

Registry与DGC的攻击利用
0x01 2022-02-03写的一篇文章。 0x02 Registry Registry指的是RMI的注册表,攻击的目标是注册表所在的机器,一般注册表和RMI Server在同一个机器上,特殊情况下也会在不同机器上。 在我们通过LocateRegistry#getRegistry获取到目标开启的注…...

赛道持续降温!又一家自动驾驶公司裁员,市值曾超50亿美元
从去年下半年开始,自动驾驶赛道的裁员、倒闭风潮盛行。 本周,美股卡车自动驾驶上市公司Embark Trucks(EMBK)宣布将裁员70%,同时大幅缩减业务。“痛苦可能还没有结束,”公司首席执行官Alex Rodrigues在给员…...

路径规划 | 图解动态A*(D*)算法(附ROS C++/Python/Matlab仿真)
目录0 专栏介绍1 什么是D*算法?2 D*算法核心概念一览3 D*算法流程图4 步步图解:算法实例5 算法仿真与实现5.1 ROS C实现5.2 Python实现0 专栏介绍 🔥附C/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备!详…...
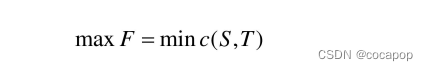
GraphCut、最大流最小割定理
G(V,E);V为点集,E为边集; 节点集V中的节点分为: (1)终端节点。不包含图像像素,用S和T表示。S为源点,T为汇点。图像分割中通常用S表示前景目标&a…...

Word文档的密码忘记了怎么办?
Word文档可以设置两种密码,文件的“限制密码”和“打开密码”,今天来分享一下忘记这两种密码可以如何处理。 如果忘记的是Word文档的“限制密码”,文档就无法编辑及更改了,菜单目录中的相关选项也都是灰色状态,无法点…...

Java分布式事务(二)
文章目录🔥分布式事务处理_认识本地事务🔥关系型数据库事务基础_并发事务带来的问题🔥关系型数据库事务基础_MySQL事务隔离级别🔥MySQL事务隔离级别_模拟异常发生之脏读🔥MySQL事务隔离级别_模拟异常发生之不可重复读&…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

【堆垛策略】设计方法
堆垛策略的设计是积木堆叠系统的核心,直接影响堆叠的稳定性、效率和容错能力。以下是分层次的堆垛策略设计方法,涵盖基础规则、优化算法和容错机制: 1. 基础堆垛规则 (1) 物理稳定性优先 重心原则: 大尺寸/重量积木在下…...

spring Security对RBAC及其ABAC的支持使用
RBAC (基于角色的访问控制) RBAC (Role-Based Access Control) 是 Spring Security 中最常用的权限模型,它将权限分配给角色,再将角色分配给用户。 RBAC 核心实现 1. 数据库设计 users roles permissions ------- ------…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...
)
使用python进行图像处理—图像滤波(5)
图像滤波是图像处理中最基本和最重要的操作之一。它的目的是在空间域上修改图像的像素值,以达到平滑(去噪)、锐化、边缘检测等效果。滤波通常通过卷积操作实现。 5.1卷积(Convolution)原理 卷积是滤波的核心。它是一种数学运算,…...
