Matlab偏微分方程拟合 | 完整源码 | 视频教程
专栏导读
- 作者简介:工学博士,高级工程师,专注于工业软件算法研究
- 本文已收录于专栏:《复杂函数拟合案例分享》本专栏旨在提供 1.以案例的形式讲解各类复杂函数拟合的程序实现方法,并提供所有案例完整源码;2.复杂函数包含:分段函数、积分函数、常/偏微分函数、隐函数、方程组、级数函数、多参数函数;3.拟合工具是Matlab种的lsqcurvefit, nlinfit,神经网络,ga遗传算法,MultiStart全局优化算法等;4.拟合案例均源自科研实践中遇到的案例,文本教程+视频教程+案例源码,三向强化学习!提高大家解决实际数学建模的问题。
- 【源码获取链接】Matlab偏微分方程拟合 | 源码分享 | 视频教程
- 【视频课程地址】https://www.bilibili.com/video/BV1bQ4y1U7mu/?spm_id_from=333.337.search-card.all.click
- 欢迎订阅专栏,订阅用户可私聊进入Matlab编程交流群(知识交流、问题解答),并获赠丰厚的Matlab相关学习资料(教材、源码、视频课)
- 专栏订阅地址:https://blog.csdn.net/u010542847/category_12576325.html
文章目录
专栏导读
文章目录
【总体简介】💻🔍
【代码截图】
【视频课程】
【总体简介】💻🔍
你将获得: 偏微分方程拟合matlab源码 + 参考论文+视频教程
源码获取链接:Matlab偏微分方程拟合 | 源码分享 | 视频教程
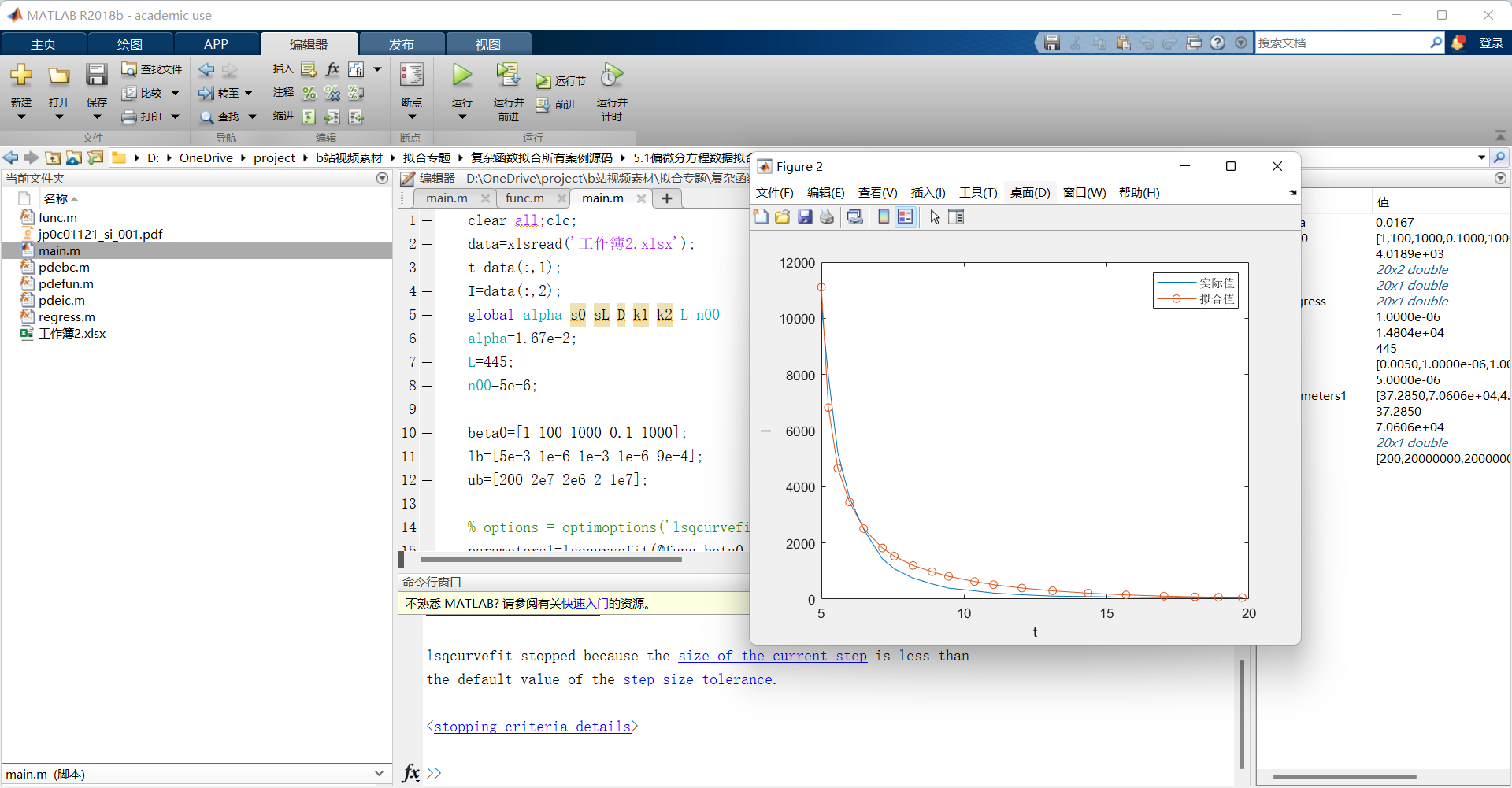
程序实现了偏微分方程中参数的拟合,具体函数形式如下图所示,函数的自变量是t,因变量是I(t),被积函数中包含的n(s,t)是通过偏微分方程求解得到,待拟合参数为k1,k2, D, s0, sL,拟合采用的工具是lsqcurvefit(),难点在于如何定义拟合函数,包含了积分运算,偏微分方程运算等内容,非常复杂。但是程序成功实现了该复杂函数的拟合。该案例源自一篇论文中的模型,也随代码一起提供给用户。
建议小伙伴在学习偏微分方程拟合前,先学习一下Matlab偏微分方程求解的课程(见文末链接)。
代码文件包含(见后文代码截图):1.实验数据离散点文件;2.main主文件;3.自定义拟合函数文件;4.偏微分方程的定义函数;5.偏微分方程边界条件定义函数

【代码截图】
【视频课程】
【Matlab复杂函数非线性拟合专题/lsqcurvefit/nlinfit/分段函数、积分函数、常/偏微分函数、隐函数、方程组、最小二乘法/机器学习/神经网络/编程/人工智能】 3.(试看)积分函数拟合(被积函数存在待定参数+积分上下限为自变量)_哔哩哔哩_bilibili
相关文章:

Matlab偏微分方程拟合 | 完整源码 | 视频教程
专栏导读 作者简介:工学博士,高级工程师,专注于工业软件算法研究本文已收录于专栏:《复杂函数拟合案例分享》本专栏旨在提供 1.以案例的形式讲解各类复杂函数拟合的程序实现方法,并提供所有案例完整源码;2.…...
)
什么是yocto基本组件(bitbake,recipes,classes,configuration,layer)
文章目录 1基本组件1.1 bitbake1.2 Recipes1.3 Classes1.4 Configurations2 层的理解2.1 层结构2.2 nxp yocto示例2.3 ti yocto示例1基本组件 1.1 bitbake bitbake,是OpenEmbedded构建系统的核心工具,负责解析元数据,从中生成任务列表,然后执行这些任务。bitbake是一个通…...
electron 程序与安装包图标放大与制作
原因 electron-builder 在打包时需要最小支持到256x256像素的icon图标。原有历史图标都太小了。需要尝试将图标放大。 工具 convertio.co/zh/ico-png/ 在线ico转png网站 https://github.com/upscayl/upscayl 图片放大工具 csdn下载 greenfish-icon-editor-pro.en.softonic.c…...
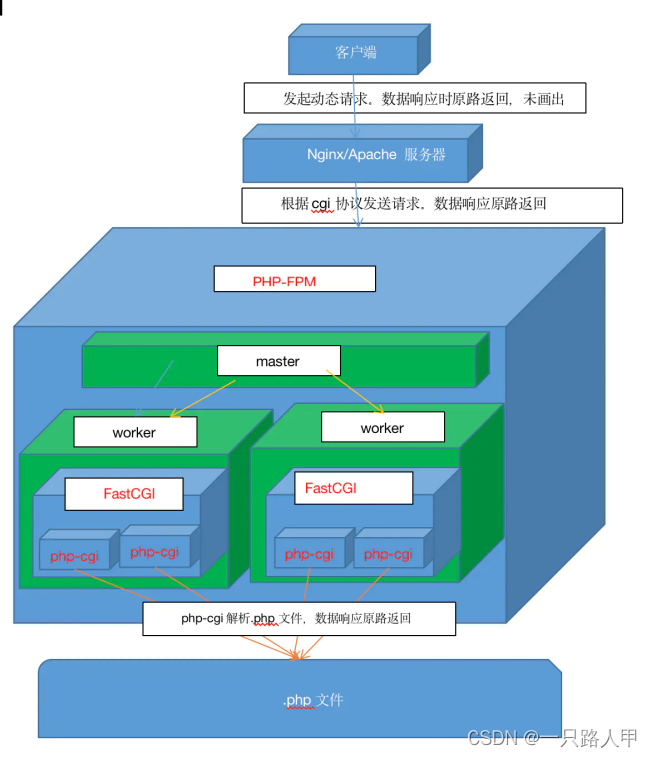
nginx,php-fpm
一,Nginx是异步非阻塞多进程,io多路复用 1、master进程:管理进程 master进程主要用来管理worker进程,具体包括如下4个主要功能: (1)接收来自外界的信号。 (2)向各worker进…...

网络编程(3/4)
广播 #include<myhead.h>int main(int argc, const char *argv[]) {//1、创建套接字int sfd socket(AF_INET, SOCK_DGRAM, 0);if(sfd -1){perror("socket error");return -1;}//2、将套接字设置成允许广播int broadcast 1;if(setsockopt(sfd, SOL_SOC…...

vue computed计算属性
模板中的表达式虽然方便,但也只能用来做简单的操作;如果在模板中写太多逻辑,会让模板变得臃肿,难以维护;因此我们推荐使用计算属性来描述依赖响应式状态的复杂逻辑 1. 选项式 API 中,可以提供computed选项来…...

智慧路灯物联网管理平台及应用
资产维护 路灯物联网涉及的设备数量大,种类多,生产厂家和批次多样化,对路灯物联网的资产维护是一项艰巨的工作。资产维护管理能够有效的管理路灯资产及各类传感设备资产信息,实现精细化管理。平台提供了对集中控制器、各感测设备节点控制器等设备的信息进行管理,包括录入…...
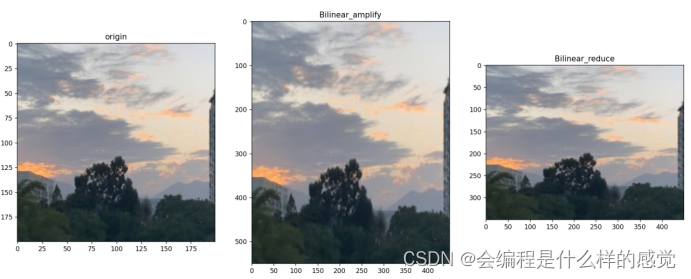
基于OpenCV的图形分析辨认02
目录 一、前言 二、实验目的 三、实验内容 四、实验过程 一、前言 编程语言:Python,编程软件:vscode或pycharm,必备的第三方库:OpenCV,numpy,matplotlib,os等等。 关于OpenCV&…...

python基础——基础语法
文章目录 一、基础知识1、字面量2、常用值类型3、注释4、输入输出5、数据类型转换6、其他 二、字符串拓展1、字符串定义2、字符串拼接3、字符串格式化4、格式化精度控制 三、条件/循环语句1、if2、while3、for循环 四、函数1、函数定义2、函数说明文档3、global关键字 五、数据…...
vue3 vue-i18n 多语言
1. 安装 npm install vue-i18n -s 2. 引入main.js import { createI18n } from vue-i18n import messages from ./i18n/index const i18n createI18n({legacy: false,locale: Cookies.get(language) || en_us, // set localefallbackLocale: en_us, // set fallback local…...
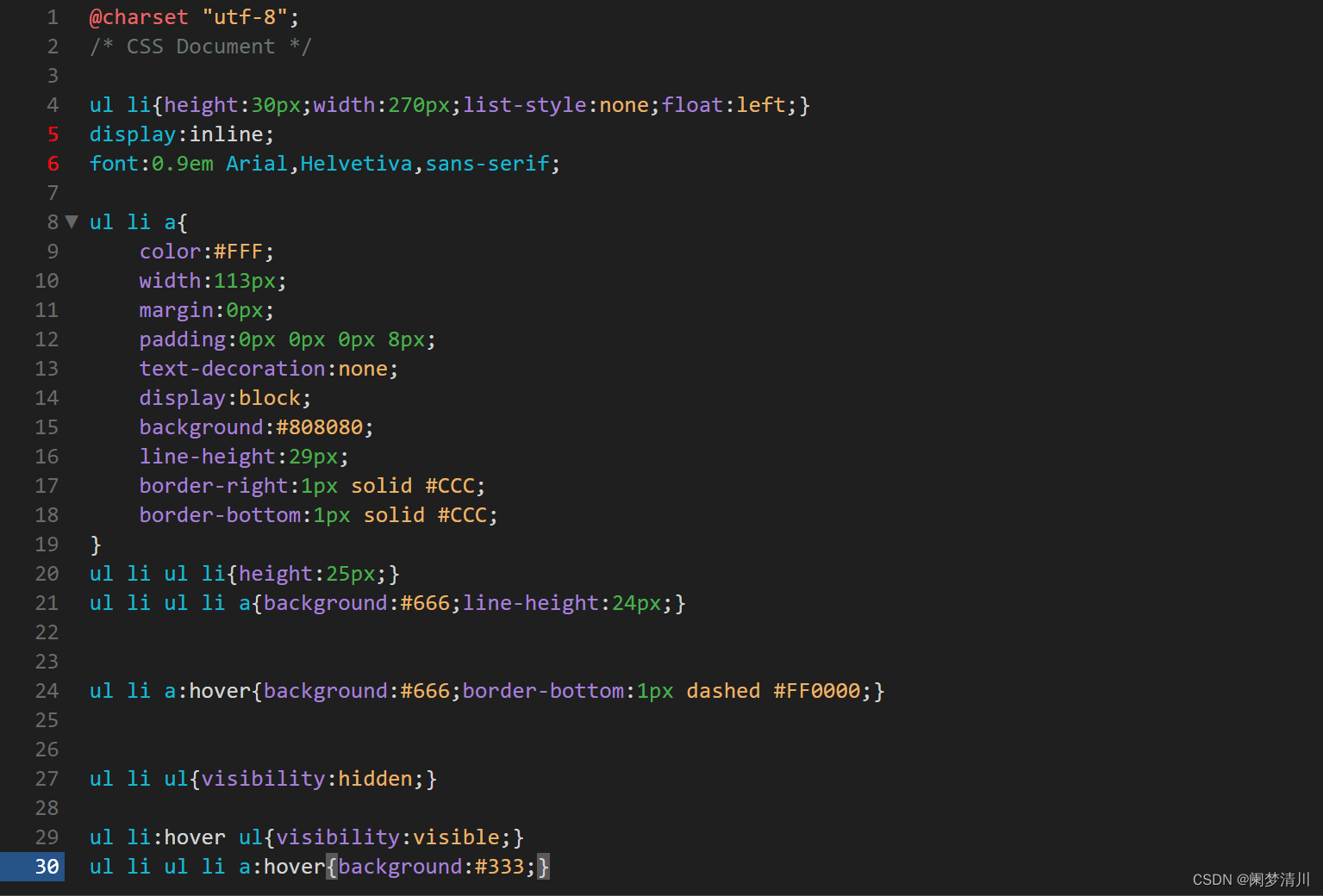
二级水平导航菜单栏的实现
1. 这个是本人设计的一带一路的二级水平导航栏HTML代码; 这里最后实现的效果是鼠标悬停在导航栏上面,就会显示下面的4个部分页面,这里只是以评论热 点作为例子,其他的类似; 2.首先要设计DIV,然后利用无…...
和mr.diffs()的区别)
在GitLab Python库中,mr.changes()和mr.diffs()的区别
在GitLab Python库中,mr.changes()和mr.diffs()都用于获取合并请求(Merge Request)中的文件更改信息,但它们之间有一些区别: mr.changes(): mr.changes() 方法返回合并请求中所有文件的更改信息。返回的结果…...

JavaScript | 【讨论】微软早在2022年已经停用ie的今天,js开发还需要考虑ie9以下的情况嘛?
CSDN的C知道机器回复: 在进行JavaScript开发时,通常需要考虑IE9以下的况。尽管IE9以下的浏览器在市场份额上逐渐减少,但仍然有一部分用户在使用这些旧版本的浏览器。为了确保网站或应用在这些浏览器上能够正常运行,以下是一些需要…...
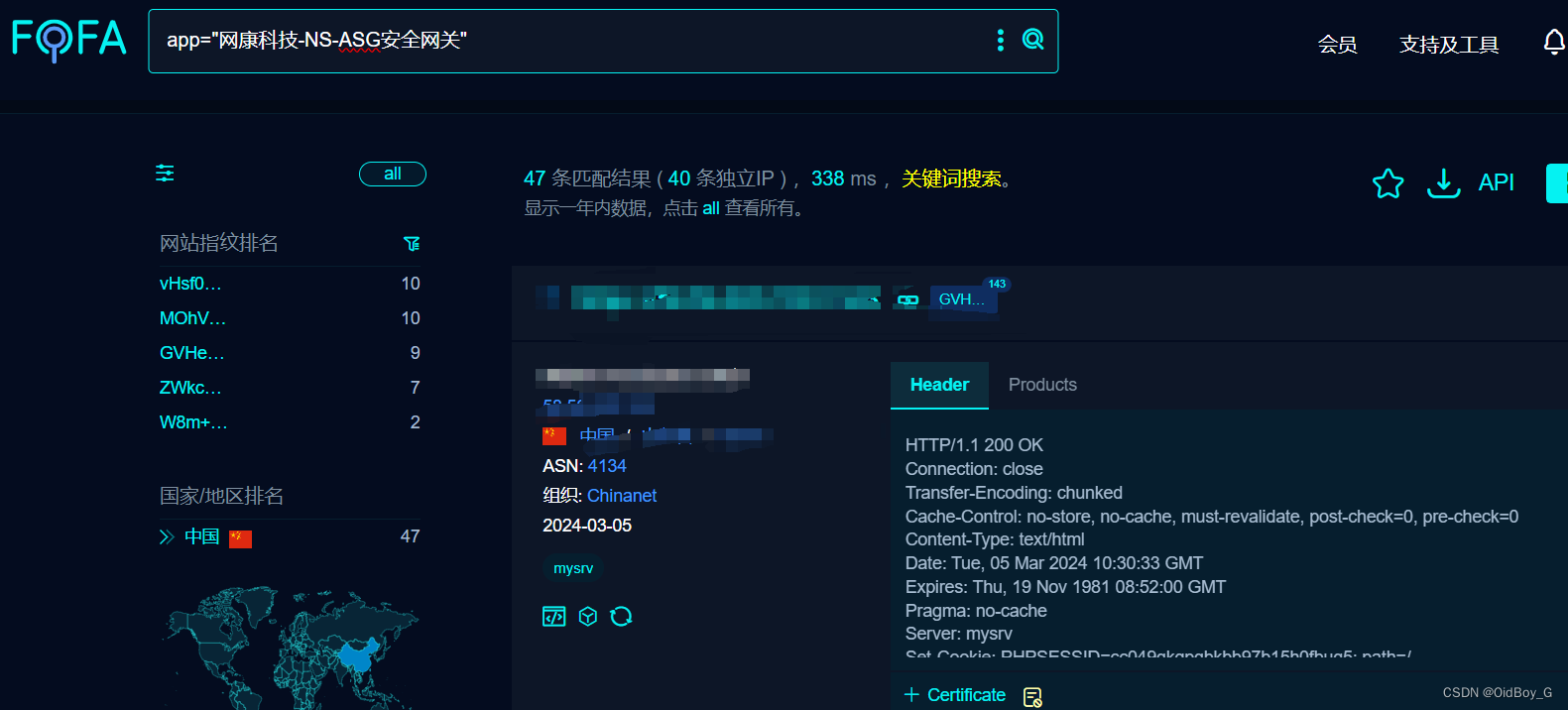
网康科技 NS-ASG 应用安全网关 SQL注入漏洞复现(CVE-2024-2022)
0x01 产品简介 网康科技的NS-ASG应用安全网关是一款软硬件一体化的产品,集成了SSL和IPSec,旨在保障业务访问的安全性,适配所有移动终端,提供多种链路均衡和选择技术,支持多种认证方式灵活组合,以及内置短信认证、LDAP令牌、USB KEY等多达13种认证方式。 0x02 漏洞概述 …...

英福康INFICON软件真空Tware32中文操作手册
英福康INFICON软件真空Tware32中文操作手册...

UnityAPI的学习——Quaternion类
Quaternion又称为四元数,由x、y、z和w这4个分量组成,属于struct类型。 在Unity中,用Quaternion来存储和表示对象的旋转角度。 Quaternion类实例属性 在Quaternion类中,涉及的实例属性主要有eulerAngles eulerAngles属性&#x…...

chromedriverUnable to obtain driver for chrome using ,selenium找不到chromedriver
1、下载chromedriver chromedriver下载网址:CNPM Binaries Mirror 老版本在:chromedriver/ 较新版本在:chrome-for-testing/ 2、设置了环境变量还是找不到chromedriverUnable to obtain driver for chrome using NoSuchDriverException:…...

剑指offer面试算法题目,自己总结的
JZ31 栈的压入、弹出序列-C++-CSDN博客 剑指 Offer(C++版本)系列:从尾到头打印单链表(C++)-CSDN博客 剑指offer》15--二进制中1的个数[C++]-CSDN博客 《剑指offer》14--剪绳子(整数拆分)[C++]-CSDN博客 剑指 Offer 12. 矩阵中的路径-CSDN博客 C++--机器人的运动范围…...
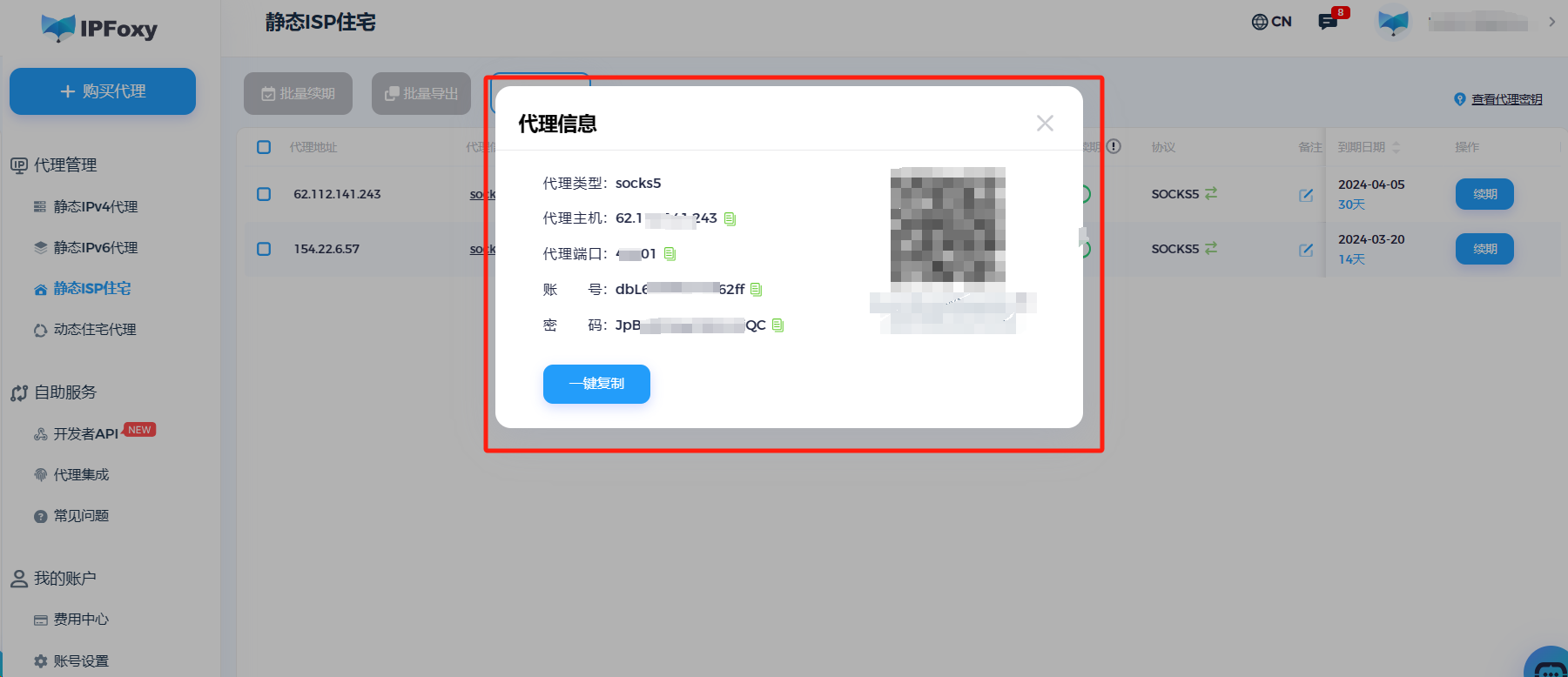
原生IP是什么?如何测试代理是不是原生IP?
一、什么是原生IP 原生IP地址是互联网服务提供商(ISP)直接分配给用户的真实IP地址,无需代理或转发。这类IP的注册国家与IP所在服务器的注册地相符。这种IP地址直接与用户的设备或网络关联,不会被任何中间服务器或代理转发或隐藏。…...
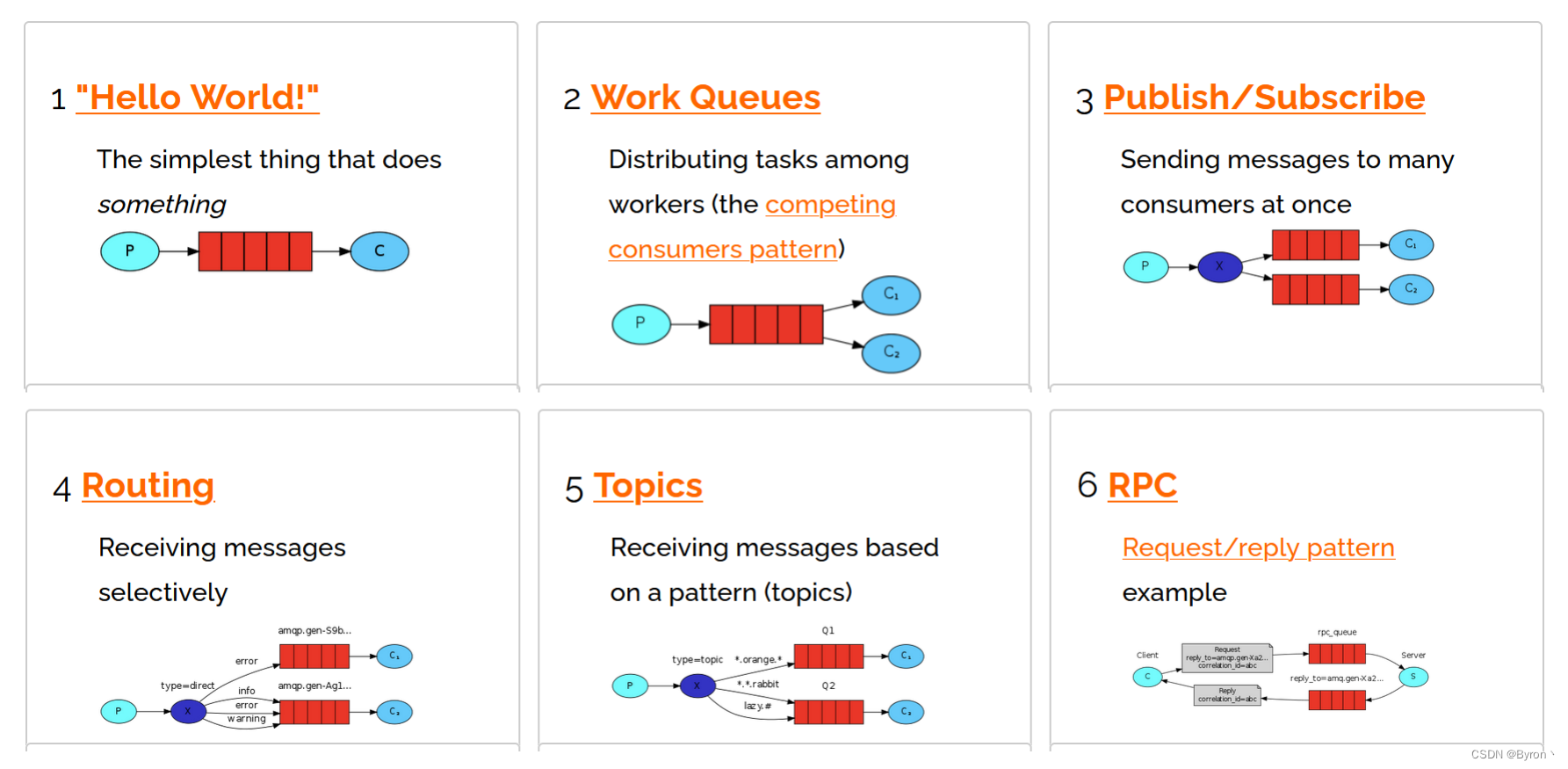
1、MQ_介绍、优缺点、类型等
MQ介绍 1. MQ概述 MQ(Message Queue):消息队列,是基础数据结构中FIFO(first in first out)的一种数据结构。一般用来解决流量削峰、应用解耦、异步处理等问题,实现高性能,高可用&a…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...
