Codeforces Round 883 (Div. 3)(集训队加训1)
A.如果钉子与地面距离大于绳子的长度就必须剪
#include<bits/stdc++.h>
#define eps 1e-5
#define INF 1e9
using namespace std;
typedef long long ll;
const int N = 2e6 + 9;
int a[N],b[N],cl[N];
void Lan(){int n;cin>>n;for(int i=1;i<=n;i++){cin>>a[i]>>b[i];}ll ans=0;for(int i=1;i<=n;i++){if(a[i]>b[i]){ans++;}}cout<<ans<<'\n';
}
int main() {ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);int q;cin>>q;while (q--) {Lan();}return 0;
}B.
暴力枚举横竖2个斜
#include<bits/stdc++.h>
#define eps 1e-5
#define INF 1e9
using namespace std;
typedef long long ll;
const int N = 2e3 + 9;
char a[N][N];
void Lan(){for(int i=3;i<=5;i++){for(int j=3;j<=5;j++){cin>>a[i][j];}}for(int i=3;i<=5;i++){for(int j=3;j<=5;j++){if(a[i][j]=='.'){continue;}if(a[i][j]==a[i+1][j+1] && a[i][j]==a[i+2][j+2]){cout<<a[i][j]<<'\n';return;} if(a[i][j]==a[i+1][j] && a[i][j]==a[i+2][j]){cout<<a[i][j]<<'\n';return;}if(a[i][j]==a[i][j+1] && a[i][j]==a[i][j+2]){cout<<a[i][j]<<'\n';return;}if(a[i][j]==a[i-1][j+1] && a[i][j]==a[i-2][j+2]){cout<<a[i][j]<<'\n';return;}}}cout<<"DRAW"<<'\n';
}
int main() {ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);int q;cin>>q;while (q--) {Lan();}return 0;
}C.
贪心一下,然后结构体排序即可
#include<bits/stdc++.h>
#define eps 1e-5
#define INF 1e9
using namespace std;
typedef long long ll;
const int N = 2e5 + 9;
ll t[N],prefix[N];
struct node{ll score,t,index;
}a[N];
bool cmp(node a,node b){return (a.score==b.score?(a.t==b.t?a.index<b.index:a.t<b.t):a.score>b.score);//排序
}
void Lan(){int n,m,h;cin>>n>>m>>h;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>t[j];}sort(t+1,t+1+m);//在矩阵中每行排序for(int j=1;j<=m;j++){prefix[j]=prefix[j-1]+t[j];//前缀和}ll res=0;int k;for(k=1;k<=m;k++){if(prefix[k]>h){break;}res+=prefix[k];}a[i].score=k,a[i].t=res,a[i].index=i;//存储}sort(a+1,a+1+n,cmp);for(int i=1;i<=n;i++){//找index==1if(a[i].index==1){cout<<i<<'\n';return;}}
}
int main() {ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);int q;cin>>q;while (q--) {Lan();}return 0;
}D.
先算不重叠的,再用相似三角形算重合面积
#include<bits/stdc++.h>
#define eps 1e-5
#define INF 1e9
using namespace std;
typedef long double ld;
const int N = 2e5 + 9;
int a[N],diff[N];
void Lan(){ld n,d,h;cin>>n>>d>>h;for(int i=1;i<=n;i++){cin>>a[i];}ld ans=n*d*h/2;for(int i=1;i<=n-1;i++){if(a[i]+h>a[i+1]){diff[i]=a[i]+h-a[i+1];}else{diff[i]=0;}}for(int i=1;i<=n-1;i++){//diff[i]/x=h/d->x*h=d*diff[i];->x=d*diff[i]/hif(diff[i]){ans-=(d*diff[i]/h)*(diff[i])/2;}}cout<<fixed<<setprecision(6)<<ans<<'\n';
}
int main() {ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);int q;cin>>q;while (q--) {Lan();}return 0;
}E1-E2.
暴力枚举1e6,后面最多到k*k二分即可
#include<bits/stdc++.h>
#define eps 1e-5
#define INF 1e9
using namespace std;
typedef long long ll;
const int N = 2e6 + 9;
int a[N];
set<ll> st;
void Lan(){ll n;cin>>n;if(st.count(n)){cout<<"YES"<<'\n';}else{ll x=sqrt(n);if(x>1 && x*(x+1)==n-1){cout<<"YES"<<'\n';}else{cout<<"NO"<<'\n';}}
}
void init(){for(ll i=2;i<=1e6;i++){ll x=1+i+i*i;ll y=i*i;st.insert(x);while(1){if(1.0*y>1.0*1e18/i){break;}y*=i;x+=y;if(x>1e18){break;}st.insert(x);}}
}
int main(){ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);init();int q;cin>>q;while (q--) {Lan();}return 0;
}F.
思路好想的交互,但是写很shi
#include<bits/stdc++.h>
#define eps 1e-5
#define INF 1e9
using namespace std;
typedef long long ll;
const int N = 2e6 + 9;
int a[N],c[N],fzc[N];
/*变了就删去不是这个数字的等下一次变把不是这个数字的发送即可不能固定等第2次是否变如果第一次变了不变了第三次变了第四次不变就会wa*/
void Lan(){int n;cin>>n;for(int i=1;i<=9;i++){//初始化!c[i]=0;fzc[i]=0;}for(int i=1;i<=n;i++){cin>>a[i];}for(int i=1;i<=n;i++){//记录现在的数字种类以及数量c[a[i]]++;}cout<<"-"<<" "<<0<<endl;//第一次for(int i=1;i<=n;i++){cin>>a[i];}int keynum=0;//找多的,从少的变到多的for(int i=1;i<=n;i++){fzc[a[i]]++;}for(int i=1;i<=9;i++){if(fzc[i]>c[i]){keynum=i;break;}}if(!keynum){for(int i=1;i<=9;i++){fzc[i]=0;}cout<<'-'<<" "<<0<<endl;//必然要换了 for(int i=1;i<=n;i++){cin>>a[i]; }for(int i=1;i<=n;i++){fzc[a[i]]++;}for(int i=1;i<=9;i++){if(fzc[i]>c[i]){keynum=i;break;}}}vector<int> del;//可以删去的数字for(int i=1;i<=n;i++){if(a[i]!=keynum){del.push_back(i);}}cout<<"-"<<" "<<(int)del.size()<<" ";for(auto &i : del){cout<<i<<" ";}cout<<endl;for(int i=1;i<=9;i++){//清空c[i]=0;fzc[i]=0;}//结束上述过程后数组其实只存在一个数字,因此等2轮找不是这个数字的index即可for(int i=1;i<=n-(int)del.size();i++){//得到数组只是接受一下回复信息cin>>a[i];}ll ansindex=0;for(int i=1;i<=n-(int)del.size();i++){if(a[i]!=keynum){ansindex=i;break;}}if(ansindex){cout<<"!"<<" "<<ansindex<<endl;return;}cout<<"-"<<" "<<0<<endl;//这轮结束后必然会有换的for(int i=1;i<=n-(int)del.size();i++){cin>>a[i];}for(int i=1;i<=n;i++){//找到对应indexif(a[i]!=keynum){ansindex=i;break;}}cout<<"!"<<" "<<ansindex<<endl;
}
int main() {// ios::sync_with_stdio(false);// cin.tie(0),cout.tie(0);int q;cin>>q;while (q--) {Lan();}return 0;
}相关文章:
(集训队加训1))
Codeforces Round 883 (Div. 3)(集训队加训1)
A.如果钉子与地面距离大于绳子的长度就必须剪 #include<bits/stdc.h> #define eps 1e-5 #define INF 1e9 using namespace std; typedef long long ll; const int N 2e6 9; int a[N],b[N],cl[N]; void Lan(){int n;cin>>n;for(int i1;i<n;i){cin>>a[i]…...
)
自封装 bind 方法(二)
因为 bind 的使用方法是 某函数.bind(某对象,...剩余参数) 所以需要在 Function.prototype 上进行编程将传递的参数中的某对象和剩余参数使用 apply 的方式在一个回调函数中执行即可要在第一层获取到被绑定函数的 this,因为要拿到那个函数用 apply /***…...
vcomp140.dll丢失如何修复,5种修复方法轻松搞定vcomp140.dll问题
vcomp140.dll文件的丢失可能会引发一系列系统运行与软件功能上的问题。具体来说,这个动态链接库文件是Visual C Redistributable的一部分,对于许多基于此环境开发的应用程序至关重要。一旦缺失,可能会导致部分应用程序无法正常启动或运行&…...
和机器视觉(Machine Vision))
计算机视觉(Computer Vision)和机器视觉(Machine Vision)
举例说明计算机视觉(CV)技术的优势和挑战 计算机视觉(CV)技术是一种使用计算机科学和机器学习方法来解释、分析和理解图像和视频的技术。它的优势和挑战如下: 优势: 高效性:CV技术可以快速处…...

国内用ChatGPT可以吗
PS: 无限次数,无需魔法,登录即可使用,网页打开下面 tj4.mnsfdx.net 点击跳转链接 国内用ChatGPT可以吗?简单来说,是可以的,国内可以使用ChatGPT。ChatGPT是一款实体机器翻译工具,也是一种人工智能技术&…...

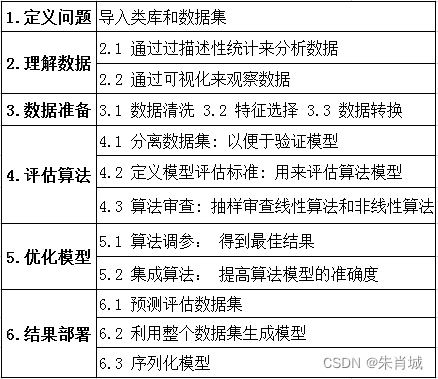
数据分析-Pandas两种分组箱线图比较
数据分析-Pandas两种分组箱线图比较 数据分析和处理中,难免会遇到各种数据,那么数据呈现怎样的规律呢?不管金融数据,风控数据,营销数据等等,莫不如此。如何通过图示展示数据的规律? 数据表&am…...

Mac版2024 CleanMyMac X 4.14.6 核心功能详解以及永久下载和激活入口
CleanMyMac 是 macOS 上久负盛名的系统清理工具,2018 年,里程碑式版本 CleanMyMac X 正式发布。不仅仅是命名上的变化,焕然一新的 UI、流畅的动画也让它显得更加精致。新增的系统优化、软件更新等功能,使得在日常使用 macOS 时有了…...

Java引用传递及基本应用
在 Java 中,传递参数的方式主要有两种:值传递(传递的是对象的引用值)和引用传递。本教程将重点介绍 Java 中的引用传递以及其基本应用。 1. 引用传递概念 在 Java 中,所有的方法参数都是通过值传递的。对于对象类型的…...

低代码测试自动化
每个企业都希望将产品快速推向市场。虽然低代码无代码测试自动化可以帮助组织实现这一目标,但测试人员必须牢记几件事,才能通过低代码无代码来推进他们的组织。 低代码测试自动化的重要性是什么? 低代码测试自动化加速了测试生命周期。借助简…...

Linux 文件操作命令
1 文件与目录操作 cd /home 进入 ‘/home’ 目录 cd .. 返回上一级目录cd ../.. 返回上两级目录cd - 返回上次所在目录cp file1 file2 将file1复制为file2cp -a dir1 dir2 复制一个目录 cp -a /tmp/dir1 . 复制一个…...
机器学习-面经(part8、贝叶斯和其他知识点)
机器学习面经其他系列 机器学习面经系列的其他部分如下所示: 机器学习-面经(part1)-初步说明 机器学习-面经(part2)-交叉验证、超参数优化、评价指标等内容 机器学习-面经(part3)-正则化、特征工程面试问题与解答合集机器学习-面经(part4)-决策树共5000字的面试问…...
)
图数据库 之 Neo4j - 应用场景3 - 知识图谱(8)
背景 知识图谱的复杂性:知识图谱通常包含大量的实体、关系和属性,以及它们之间的复杂关联。传统的关系型数据库在处理这种复杂性时可能面临性能和灵活性的挑战。 图数据库的优势:图数据库是一种专门用于存储和处理图结构数据的数据库。它们使用节点和边来表示实体和关系,并…...

redis 性能优化三
前言 如果Redis 没有执行大量的慢查询,同时也没有删除大量的过期的keys,那么我们该怎么办呢?那么我们是不是就应该关注影响性能的其他机制了,也就是文件系统和操作系统了。 Redis 会把数据持久化到磁盘,这个过程依赖文件系统来完…...

Python用Tkinter实现圆的半径 面积 周长 知一求二程序
Python用Tkinter实现圆的半径 面积 周长 知一求二程序 import tkinter as tk from tkinter import messagebox from tkinter import *app tk.Tk() app.title(圆的半径 面积 周长 知一求二程序) app.geometry(425x125)label1 tk.Label(app, text"半径") label2 tk.…...

电源环路补偿的目标是避免产生正反馈
在一般的认识中,进行电源环路设计的目的是保证电源输出端的电压稳定,在误差信号传入系统时,系统进行负反馈调节,矫正干扰信号带来的误差量。 那么,为什么要设置成这样,不稳定会有什么后果等等,…...

SSM+MySQL替换探索 openGauss对比postgresql12
SSM 介绍 SSM(SpringSpringMVCMyBatis)框架集由 Spring、MyBatis 两个开源框架整合而成(SpringMVC 是 Spring 中的部分内容),常作为数据源较简单的 web 项目的框架。 Spring Spring 就像是整个项目中装配 bean 的大…...
XGboost的整理
XGboost(extreme gradient boosting):高效实现了GBDT算法并进行了算法和工程上的许多改进。 XGboost的思路: 目标:建立k个回归树,使得树群的预测尽量接近真实值(准确率)而且有尽量大的泛化能力…...

java入门基础学习导览
本篇文章会持续更新直到更新完毕,关注博主不迷路~(如果没有超链接,表示还没有更新到) 一 JAVA语言基础 二 流程控制 三 数组 字符串 与正则表达式 四 JAVA面向对象编程 五 JAVA 异常处理 六 JAVA输入输出 七 泛型与容器类 …...

网工内推 | 上市公司售前,大专以上即可,最高15K*13薪,补贴多
01 北京神州新桥科技有限公司 招聘岗位:售前工程师 职责描述: 1、完成项目的售前技术支持工作; 2、 配合销售进行新产品及解决方案的推广工作; 3、 配合销售完成用户的售前技术交流方案准备、现场技术交流、技术方案宣讲等工作…...
JAVA开发第一个Springboot WebApi项目
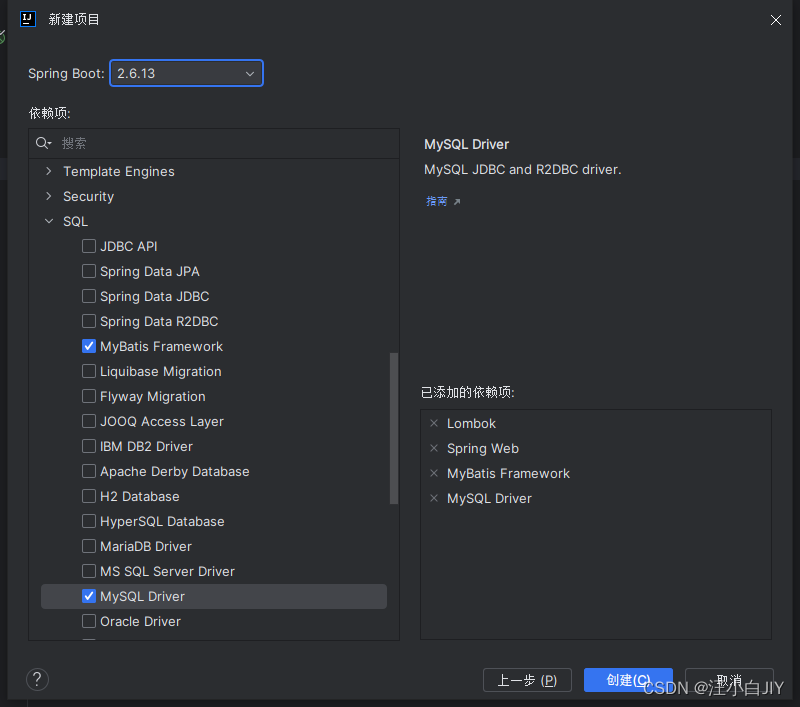
一、创建项目 1、用IDEA新建一个SpringBoot项目 注意JDK与Java版本的匹配,如果想选择jdk低版本,先要更改服务器URL:start.aliyun.com 2、添加依赖 (1)、Lombok (2)、Spring Web (3)、Mybatis Framework (4)、MySqlDriver 项目中的配置 pom.xml 如下 <?…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...
