2016年认证杯SPSSPRO杯数学建模C题(第一阶段)如何有效的抑制校园霸凌事件的发生解题全过程文档及程序
2016年认证杯SPSSPRO杯数学建模
C题 如何有效的抑制校园霸凌事件的发生
原题再现:
近年来,我国发生的多起校园霸凌事件在媒体的报道下引发了许多国人的关注。霸凌事件对学生身体和精神上的影响是极为严重而长远的,因此对于这些情况我们应该给予高度的重视。霸凌是各种形式校园暴力中的一种,从某种意义上说,也是危害程度较高的一种。不同于偶发的暴力事件,霸凌行为通常伴随着肉体与精神的双重伤害,并且这种伤害通常会持续很长时间,有时可能会对受害者的心灵产生终身创伤。如果没有受到专业的心理引导,受害者有可能转变为报复社会的人,进而从受害者转变为施暴者,将自己的遭遇原封不动或放大百倍地转嫁到他人身上。
2015 年 6 月 21 日,一段“小学生被多人围殴”的视频在网上广泛传播。据网民爆料,浙江省丽水市庆元县几名初中生把一名小学一年级的学生关在黑屋子里暴力殴打,并用香烟头烫伤小孩。6 月 21 日晚 8 时左右,著名演员陈坤在微博上转发了这一视频。媒体人“大鹏看天下”当晚也在微博上呼吁公安部门立即介入,“别再手软,此类事件必须严惩,结果广为通报!”多名网络“大 V”的关注,让这一事件迅速发酵为热点。不少网民震惊于视频中的情景,慨叹“校园霸凌现象竟严重至此”。
科学技术的飞速发展和互联网的普及,给青少年带来的不仅仅是积极的影响。很多初中生表示曾遭受手机、互联网上的谩骂、侮辱等新型暴力行为的影响。网络霸凌的暴力行为由于侮辱性信息传播速度快,因此造成了更直接的伤害。此外,信息扩散范围速度极快,往往来不及阻止信息的传播,也来不及保护学生,就已经对受害者造成了极大程度的伤害。
驱使青少年施加网络暴力行为的原因很多,但最主要的诱因还是年龄。青少年由于年龄较小,不够成熟,不知道如何应对和转化暴力性冲动,才造成对自身和他人的伤害。我们设计了一次针对不同年龄段青少年的心理状况的问卷调查,试图建立一个模型来判断青少年存在一些潜在心理问题的可能性。调查分为 5 个年龄段,这要涉及生命教育、生活方式、娱乐三个领域,分别包括正向和负向两个框架。其中因变量被设计成一种二选一式的评价变量,使用 A 或 B 来表示。自变量包括风险偏好、认知需要(包括 18 个题目)、决策风格(包括理智型、直觉型、依赖型、回避型、冲动型,这 5 个维度,每个维度下包括 5 个题目)三个主要方面,每个方面的题目可以按照选择的答案来计算相应的得分。调查的结果如附件一所示。
第一阶段问题:
1. 通过统计分析,请判断各个年龄段的心理状况是否有显著的差异。
2. 请建立合理的数学模型,分析不同框架的主要影响因素。并给当地报纸写一份 500 字左右的分析报告,阐述你对抑制校园霸凌事件发生的主要策略。
整体求解过程概述(摘要)
鉴于当今社会校园霸凌事件发生频繁,对此,以青少年各年龄段的心理状况为研究对象,利用影响心理状况的自变量的均值,方差及主成分分析的方法,通过建立各年龄段的心理状况显著性差异模型,判断了各年龄段心理状况的显著差异性,并进一步通过层次分析法和经典的多元线性回归方法建立数学模型,分析不同框架的主要影响因素。
针对问题一,先对所给自变量的数据进行预处理,剔除异常点,提高研究变化趋势准确性,用预处理后的数据进行均值比较,作出相应折线图,并分析了不同年龄段的自变量的差异性。再利用统计软件对均值处理后的不同年龄段的各自变量(处理后的数据)进行主成分分析和因子分析,得出新的主因子,再对新的主因子建立方差和标准差统计模型,最后根据新的心理状况因子的方差浮动,得出各年龄段的心理状况具有显著差异。
针对问题二,先选取正负两个框架中生命健康、生活方式、娱乐三个领域的评价变量 A、B,建立 0-1 整数规划赋值并求出各年龄各领域各框架的因变量均值。再利用统计软件对所有自变量进行主成分分析,建立不同框架的主要影响因素模型。并判断出(基于)正向和负向框架的新主要影响因素的主因子分别为理智性、孤独化、情绪化、冒险性、探索性、好奇性,然后定性和定量的分析不同框架的主因子,建立经典的线性回归分析模型,并通过灵敏度分析和残差分析论证了模型具有合理性。
针对问题三,为了抑制校园霸凌事件的发生,先基于青少年的心理与性格上的偏差,进行预防分析。再从青少年所需要的心理疏导出发,以家庭教育和学校教育为主要方法,鼓励青少年多做心理健康咨询,从而完善青少年的心理教育。
问题分析:
问题一
数据统计的经过是一个漫长的过程,在题目所给的数据中,需要进行预处理,剔除异常点,提高研究变化趋势准确性。对于各组变量之间的变化趋势研究,选取统计分析模型,分析得出不同年龄阶段的心理状况是否具有差异。
问题二
针对问题二,先选取正负两个框架中生命健康、生活方式、娱乐三个领域的评价变量 A、B,建立 0-1 整数规划赋值并求出各年龄各领域各框架的因变量均值。再利用统计软件对所有自变量进行主成分分析,建立不同框架的主要影响因素模型。并判断出(基于)正向和负向框架的新主要影响因素的主因子分别为理智性、孤独化、情绪化、冒险性、探索性、好奇性,然后定性和定量的分析不同框架的主因子,建立经典的线性回归分析模型,并通过灵敏度分析和残差分析论证了模型具有合理性。
问题三
问题一和问题二分析出的影响青少年心理健康状况最主要因素为理论依旧,给当地报纸写一份关于如何抑制校园霸凌事件的分析报告。
模型假设:
1.假设各个自变量之间线性无关;
2.假设问卷调查是随机发到不同年龄青少年;
3.假设 20 岁以后人生观价值观都已被定型;
4.假设心理状况只与题目所给的变量有关
5.假设题目所给的数据真实有效。
论文缩略图:


全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
部分程序代码:(代码和文档not free)
x1=[39.4185 43.1658 41.2763 42.4197 42.1404 42.0199 43.8203 42.8558 43.6504
43.8374 41.7484]';
x2=[69.7317 68.2591 69.1439 69.7185 69.6003 69.0389 72.1123 67.9125 68.0461
69.6964 66.9077]';
x3=[12.0865 11.6107 12.5586 12.7965 12.2401 12.1428 13.1944 12.8017 12.7382
12.4204 11.8073]';
y=[0.7125 0.4804 0.548 0.5094 0.4057 0.4545 0.4874 0.5042 0.4379 0.3981
0.2687];
X=[ones(length(y),1) x1,x2,x3];
Y=y';
[b,bint,r,rint,stats]=regress(Y,X)
b,bint,stats
x1=[39.4185 43.1658 41.2763 42.4197 42.1404 42.0199 43.8203 42.8558 43.6504
43.8374 41.7484]';
x2=[69.7317 68.2591 69.1439 69.7185 69.6003 69.0389 72.1123 67.9125 68.0461
69.6964 66.9077]';
x3=[12.0865 11.6107 12.5586 12.7965 12.2401 12.1428 13.1944 12.8017 12.7382
12.4204 11.8073]';
y=[0.6563 0.5 0.661 0.5377 0.5816 0.5454 0.5798 0.5214 0.5556 0.4175
0.5522];
X=[ones(length(y),1) x1,x2,x3];
Y=y';
[b,bint,r,rint,stats]=regress(Y,X)
b,bint,stats
rcoplot(r,rint)
x1=[39.4185 43.1658 41.2763 42.4197 42.1404 42.0199 43.8203 42.8558 43.6504
43.8374 41.7484]';
x2=[69.7317 68.2591 69.1439 69.7185 69.6003 69.0389 72.1123 67.9125 68.0461
69.6964 66.9077]';
x3=[12.0865 11.6107 12.5586 12.7965 12.2401 12.1428 13.1944 12.8017 12.7382
12.4204 11.8073]';
y=[0.7125 0.598 0.5989 0.5189 0.5612 0.6022 0.5294 0.4915 0.5033 0.5044
0.4029];
X=[ones(length(y),1) x1,x2,x3];
Y=y';
[b,bint,r,rint,stats]=regress(Y,X)
b,bint,stats
rcoplot(r,rint)
x1=[39.4185 43.1658 41.2763 42.4197 42.1404 42.0199 43.8203 42.8558 43.6504
43.8374 41.7484]';
x2=[69.7317 68.2591 69.1439 69.7185 69.6003 69.0389 72.1123 67.9125 68.0461
69.6964 66.9077]';
x3=[12.0865 11.6107 12.5586 12.7965 12.2401 12.1428 13.1944 12.8017 12.7382
12.4204 11.8073]';
y=[0.5687
0.4706
0.3672
0.3774
0.4337
0.4886
0.4034
0.453
0.3922
0.3451
0.3582
]';
X=[ones(length(y),1) x1,x2,x3];
Y=y';
[b,bint,r,rint,stats]=regress(Y,X)
b,bint,stats
rcoplot(r,rint)
全部论文及程序请见下方“ 只会建模 QQ名片” 点击QQ名片即可
相关文章:

2016年认证杯SPSSPRO杯数学建模C题(第一阶段)如何有效的抑制校园霸凌事件的发生解题全过程文档及程序
2016年认证杯SPSSPRO杯数学建模 C题 如何有效的抑制校园霸凌事件的发生 原题再现: 近年来,我国发生的多起校园霸凌事件在媒体的报道下引发了许多国人的关注。霸凌事件对学生身体和精神上的影响是极为严重而长远的,因此对于这些情况我们应该…...

设计模式-抽象工厂模式实践案例
抽象工厂模式(Abstract Factory Pattern)是一种创建型设计模式,它提供了一个接口,用于创建一系列相关或相互依赖的对象,而无需指定它们具体的类。抽象工厂模式是围绕一个超级工厂创建其他工厂的模式。该模式的实现涉及…...

用readproc函数读取进程的状态
概要: 本篇演示用readproc函数读取进程的状态 libprocps库的安装参考笔者的文章readproc.h-CSDN博客 演示所用的系统是Ubuntu22.04 一、代码 #include<stdio.h> #include<stdlib.h> #include<proc/readproc.h> int main() {struct PROCTAB *…...
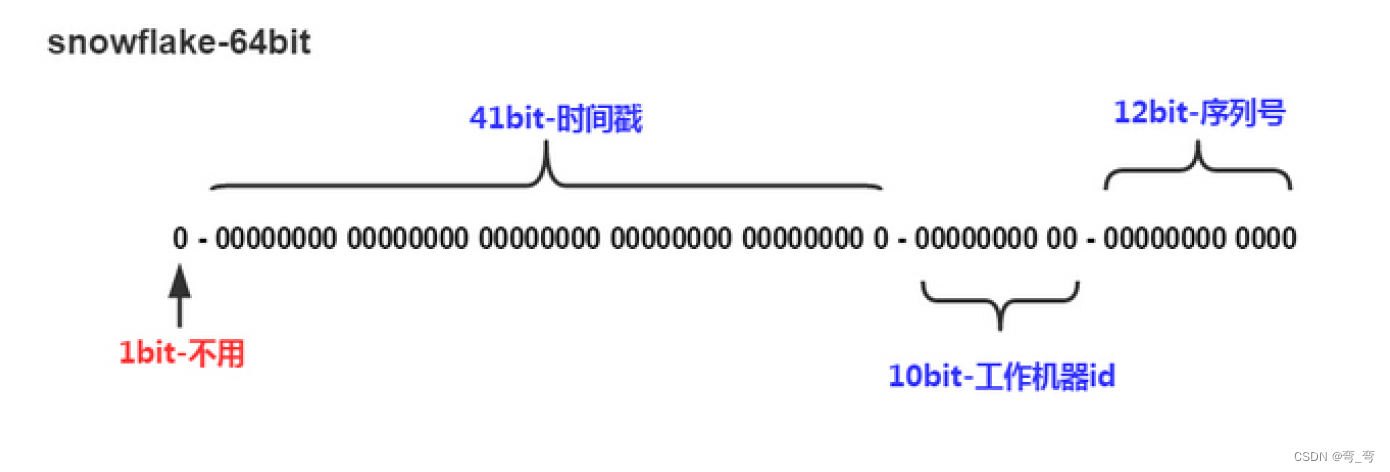
在高并发、高性能、高可用 三高项目中如何设计适合实际业务场景的分布式id(一)
分布式ID组件:黄金链路上的关键基石 在现代分布式系统中,分布式ID组件无疑扮演着至关重要的角色。作为整个系统的黄金链路上的关键组件,它的稳定性和可靠性直接关乎到整个系统的正常运作。一旦分布式ID组件出现问题,黄金链路上的…...
redis最新版本在Windows系统上的安装
一、说明 这次安装操作主要是根据redis官网说明,一步步安装下来的,英语比较好的同学,可以直接看文章底部的超链接1,跳到官网按步操作即可。 目前redis的最新稳定版本为redis7.2。 二、Windows环境改造 Redis在Windows上不被官方…...

【深度优先】【图论】【C++算法】2045. 到达目的地的第二短时间
作者推荐 视频算法专题 LeetCode2045. 到达目的地的第二短时间 城市用一个 双向连通 图表示,图中有 n 个节点,从 1 到 n 编号(包含 1 和 n)。图中的边用一个二维整数数组 edges 表示,其中每个 edges[i] [ui, vi] 表…...

思维题(蓝桥杯 填空题 C++)
目录 题目一: 编辑 代码: 题目二: 代码: 题目三: 代码: 题目四: 代码: 题目五: 代码: 题目六: 代码七: 题目八&#x…...

Meta的Llama2模型已上线!但我为何更推荐你从HuggingFace获取?还有Code Llama等你来解锁!
嘿,朋友们,今天给你们介绍一个新东西——Llama2模型,这是Meta(对,就是Facebook那家)推出的。 你可以直接去Llama的官网下载这个模型,然后按照他们GitHub上的指南来调用。 不过呢,我…...
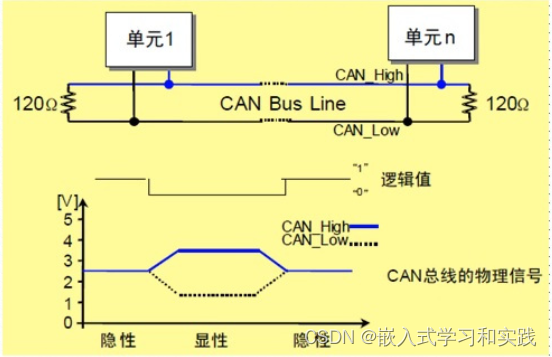
CAN总线及通讯的工作原理
一、CAN总线 CAN是控制器局域网络(Controller Area Network)的简称, 它是由研发和生产汽车电子产品著称的德国BOSCH公司开发的, 并最终成为国际标准(ISO11519),是国际上应用最广泛的现场总线之一。 二、工作原理 …...

linux下修改网卡MAC地址
我建议你使用 macchanger,但如果你不想使用它,那么可以使用另一种方法在 Linux 中更改 MAC 地址。 首先,使用以下命令关闭网卡: sudo ip link set dev enp0s31f6 down 接下来,使用以下命令设置新的 MAC:…...
47、WEB攻防——通用漏洞Java反序列化EXP生成数据提取组件安全
文章目录 序列化和反序列化的概念: 序列化:把java对象转换成字节流的过程;反序列化:把字节流恢复为java对象的过程。 对象的序列化主要有两种用途: 把对象的字节流永久的保存在硬盘上,通常存放在一个文件…...
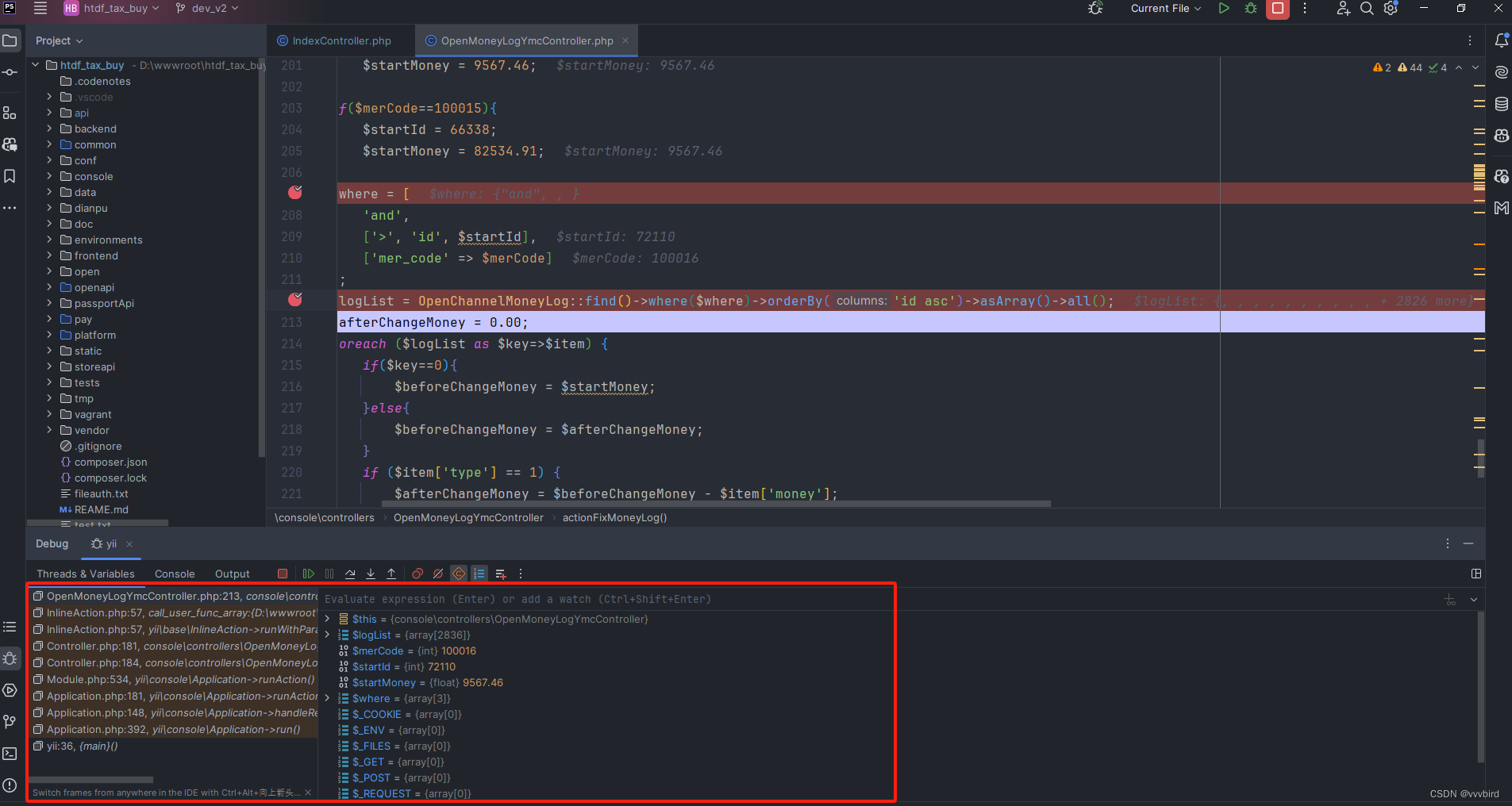
phpstorm console xdebug
1.所有配置跟浏览器http请求一样 2.记得Current File 必须是controller文件 注意:如果没有出发断点,则echo phpinfo(),查看remote_port 和phpstorm 配置是否对上。...

Vue template到render过程
Vue template到render过程 vue的模版编译过程主要如下:template -> ast -> render函数(1)调用parse方法将template转化为ast(抽象语法树)(2)对静态节点做优化(3)生…...

【你也能从零基础学会网站开发】Web建站之HTML+CSS入门篇 CSS常用属性
🚀 个人主页 极客小俊 ✍🏻 作者简介:web开发者、设计师、技术分享 🐋 希望大家多多支持, 我们一起学习和进步! 🏅 欢迎评论 ❤️点赞💬评论 📂收藏 📂加关注 CSS常用属性…...

Golang 写日志到文件
package mainimport ("log""os""time" )func main() {printLog("auto", "报警内容AA") }func printLog(filename string, content string) {t : time.Now().Format(time.DateOnly)file : filename "." t "…...
数字孪生10个技术栈:数据处理的六步骤,以获得可靠数据。
一、什么是数据处理 在数字孪生中,数据处理是指对采集到的实时或历史数据进行整理、清洗、分析和转化的过程。数据处理是数字孪生的基础,它将原始数据转化为有意义的信息,用于模型构建、仿真和决策支持。 数据处理是为了提高数据质量、整合数…...
之centos搭建jenkins)
运维随录实战(5)之centos搭建jenkins
一,搭建jenkins准备 下载安装jdk环境 -》版本 jdk11 下载安装maven环境 -》版本 maven 3.8.8 git -》版本 1.8.3.1 yum install git jenkins安装版本:2.414.3 下载地址:https://get.jenkins.io/war-stable/2.414.3/jenkins.war 注:jenkins版本与jdk版本有一定的对应关…...
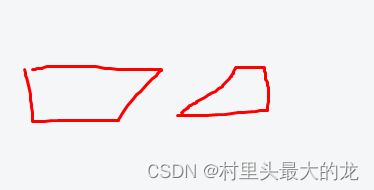
css clip-path polygon属性实现直角梯形
2024.3.8今天我学习了如何用css实现直角梯形的效果, 效果: 具体实现原理: 一、需要三个div: 外面一个大的div,里面左右两个小的div 我们需要先把第一个div变成直角梯形: 大概是这样,设置好之…...
Manz高压清洗机S11-028GCH-High Quality Cleaner 操作使用说明492页
Manz高压清洗机S11-028GCH-High Quality Cleaner 操作使用说明492页...

图像处理与视觉感知---期末复习重点(2)
文章目录 一、空间域图像增强1.1 图像增强1.2 几种变换 二、直方图2.1 直方图定义2.2 直方图均衡化2.3 离散情况2.4 例子2.5 直方图匹配2.6 例子2.7 一道例题 三、空间滤波器3.1 定义3.2 例子 四、平滑空间滤波器4.1 作用与分类4.2 线性滤波器 五、统计排序滤波器5.1 定义与分类…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
