图像处理与视觉感知---期末复习重点(2)
文章目录
- 一、空间域图像增强
- 1.1 图像增强
- 1.2 几种变换
- 二、直方图
- 2.1 直方图定义
- 2.2 直方图均衡化
- 2.3 离散情况
- 2.4 例子
- 2.5 直方图匹配
- 2.6 例子
- 2.7 一道例题
- 三、空间滤波器
- 3.1 定义
- 3.2 例子
- 四、平滑空间滤波器
- 4.1 作用与分类
- 4.2 线性滤波器
- 五、统计排序滤波器
- 5.1 定义与分类
- 5.2 计算公式
一、空间域图像增强
1.1 图像增强
1. 图像增强:是一类基本的图像处理技术,其目的是对图像进行加工,以得到对视觉解释来说视觉效果“更好”、或对机器感知效果来说“更有用”的图像。
2. 图像增强分为两类:(1) 空间域增强:对图像的像素直接处理。(2) 频域增强:对图像经傅里叶变换后的频谱成分进行处理,然后逆傅里叶变换获得所需的图像。
3. 空间域增强: g ( x , y ) = T [ f ( x , y ) ] g(x,y)=T[f(x,y)] g(x,y)=T[f(x,y)]
f ( x , y ) f(x,y) f(x,y) 是原图像; g ( x , y ) g(x,y) g(x,y) 是处理后的图像; T T T 是作用于 f f f 的操作,定义在 ( x , y ) (x,y) (x,y) 的邻域。
4. 空间域增强的简化形式: s = T ( r ) s=T(r) s=T(r)
r r r 是 f ( x , y ) f(x,y) f(x,y) 在任意点 ( x , y ) (x,y) (x,y) 的灰度级; s s s 是 g ( x , y ) g(x,y) g(x,y) 在任意点 ( x , y ) (x,y) (x,y) 的灰度级。
1.2 几种变换
1. 反转变换和对数变换:

2. 幂变换:

3. 5灰度级切片

4. 6位平面切片

二、直方图
2.1 直方图定义
1. 定义(1):
一个灰度级在范围 [ 0 , L − 1 ] [0,L-1] [0,L−1] 的数字图像的直方图是一个离散函数。 h ( r k ) = n k h(r_k)=n_k h(rk)=nk;其中 n k n_k nk 是图像中灰度级为 r k r_k rk 的像素个数, r k r_k rk 是第 k k k 个灰度级, k = 0 , 1 , 2 , . . . , L − 1 k=0,1,2,...,L-1 k=0,1,2,...,L−1。
由于 r k r_k rk 的增量是1,直方图可表示为: p ( k ) = n k p(k)=n_k p(k)=nk,即图像中不同灰度级像素出现的次数。
2. 定义(2):
一个灰度级在范围 [ 0 , L − 1 ] [0,L-1] [0,L−1] 的数字图像的直方图是一个离散函数。 p ( r k ) = n k / n p(r_k)=n_k /n p(rk)=nk/n; n n n 是图像的像素总数, n k n_k nk 是图像中灰度级为 r k r_k rk 的像素个数, r k r_k rk 是第 k k k 个灰度级, k = 0 , 1 , 2 , . . . , L − 1 k=0,1,2,...,L-1 k=0,1,2,...,L−1。
3. 两种图像直方图定义的比较:

4. 一个例子:

2.2 直方图均衡化
1. 直方图均衡化思想:就是把一幅图像变换成具有均匀分布的概率密度函数的新图像过程。

2. 先讨论连续变化图像的均衡化问题。在一幅图像中,可以认为灰度级是一个在 [ 0 , L − 1 ] [0,L-1] [0,L−1] 区间取值的随机变量 R R R。设 r r r 和 s s s 分别表示归一化了的原图像灰度级和经直方图均衡后的图像灰度级,即: ≤ r , s ≤ 1 ; s = T ( r ) ; ≤r,s≤1;s=T(r); ≤r,s≤1;s=T(r); T ( r ) T(r) T(r) 作为变换函数。
在 [ 0 , 1 ] [0,1] [0,1] 区间内的任一个 r r r 值,都可产生一个 s s s 值,如下图所示:

3. T ( r ) T(r) T(r) 作为变换函数,满足下列条件:① 在 0 ≤ r ≤ 1 0≤r≤1 0≤r≤1 内为单调递增函数,保证灰度级从黑到白的次序不变。 ② 在 0 ≤ r ≤ 1 0≤r≤1 0≤r≤1 内有 0 ≤ T ( r ) ≤ 1 0≤T(r)≤1 0≤T(r)≤1,确保映射后的像素灰度级在允许的范围内。
反变换关系为: r = T − 1 ( s ) r=T^{-1}(s) r=T−1(s); T − 1 ( s ) T^{-1}(s) T−1(s) 对 s s s 同样满足上述两个条件。
4. 计算公式:


5. 直方图均衡不一定总是好的。缺点:(1) 变换后图像的灰度级减少,某些细节消失。(2) 某些图像,如直方图有高峰,经处理后对比度不自然的过分增强。
2.3 离散情况
1. 离散情况下直方图均衡化的算法步骤:
(1) 列出原始图像的灰度级 r j r_j rj, j = 0 , 1 , 2 , . . . , L − 1 j=0,1,2,...,L-1 j=0,1,2,...,L−1
(2) 统计各灰度级的像素数目 n j n_j nj, j = 0 , 1 , . . . , L − 1 j=0,1,...,L-1 j=0,1,...,L−1
(3) 计算原始图像直方图各灰度级的频率 P R ( r j ) = n j / n P_R(r_j)=n_j/n PR(rj)=nj/n, j = 0 , 1 , . . . , L − 1 j=0,1,...,L-1 j=0,1,...,L−1
(4) 计算累计分布函数: S k = ∑ p R ( r j ) S_k=∑p_R(r_j) Sk=∑pR(rj), j = 0 , 1 , . . . , k , . . . , L − 1 j=0,1,...,k,...,L-1 j=0,1,...,k,...,L−1
(5) 把新的灰度级按就近原则转化为原灰度级: g k = I N T [ ( L − 1 ) s k + 0.5 ] g_k=INT[(L-1)s_k+0.5] gk=INT[(L−1)sk+0.5],其中 I N T INT INT 为取整
(6) 用原图像 r k r_k rk 和 g k g_k gk 的映射关系,修改原图像灰度级,获得输出图像,其直方图为近似均匀分布
2.4 例子







2.5 直方图匹配
1. 直方图匹配是指生成具有指定直方图的已处理图像。
2. 离散情况下直方图匹配的过程:

2.6 例子


2.7 一道例题


三、空间滤波器
3.1 定义

3.2 例子


四、平滑空间滤波器
4.1 作用与分类
1. 平滑空间滤波器的作用:(1) 模糊处理:去除图像中一些不重要的细节。 (2) 减小噪声。
2. 平滑空间滤波器的分类:(1) 线性滤波器:均值滤波器。 (2) 非线性滤波器:①最大值滤波器 ②中值滤波器 ③最小值滤波器
4.2 线性滤波器
1. 线性滤波器其特点是对图像中像素的计算是线性的。具体来说,这种滤波器通过对图像中的每个像素及其邻域进行线性运算来得出新的像素值。这些线性运算可以包括平滑加权求和、卷积等。
2. 作用:(1) 减小图像灰度的 “尖锐” 变化,减小噪声。(2) 由于图像边缘是由灰度尖锐变化引起的,所以也存在边缘模糊问题。
3. 计算公式:

五、统计排序滤波器
5.1 定义与分类
1. 统计排序滤波器:是一种非线性滤波器,基于滤波器所在图像区域中像素的排序,由排序结果决定的值代替中心像素的值。
2. 分类:(1) 中值滤波器:用像素领域内的中间值代替该像素。 (2) 最大值滤波器:用像素领域内的最大值代替该像素。 (3) 最小值滤波器:用像素领域内的最小值代替该像素。
5.2 计算公式

相关文章:

图像处理与视觉感知---期末复习重点(2)
文章目录 一、空间域图像增强1.1 图像增强1.2 几种变换 二、直方图2.1 直方图定义2.2 直方图均衡化2.3 离散情况2.4 例子2.5 直方图匹配2.6 例子2.7 一道例题 三、空间滤波器3.1 定义3.2 例子 四、平滑空间滤波器4.1 作用与分类4.2 线性滤波器 五、统计排序滤波器5.1 定义与分类…...

【机器学习】三要素——数据、模型、算法
机器学习三要素 数据模型模型是怎么得到的?算法 我 在学习过程中,对于“模型”和“算法”的概念不清晰,一直混淆,通过查阅了一些资料在此总结一下。 数据、模型与算法被称为机器学习的三要素,因为它们在机器学习中具有不可分割的作…...
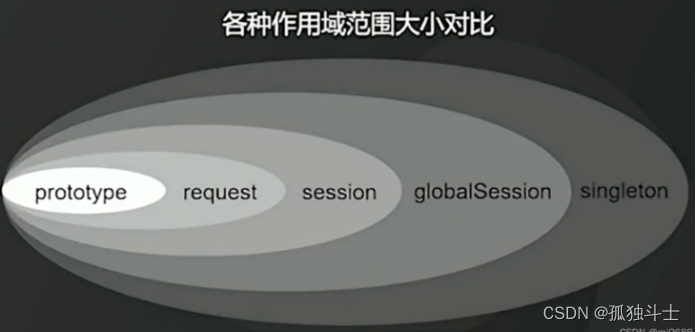
Spring框架Bean对象的五个作用域
一、前言:Bean对象简介 在Spring项目中,那些由Spring IoC容器所管理的对象,称为bean。简单地讲,bean就是由Spring容器初始化、装配及管理的对象,除此之外,bean就与应用程序中的其他对象没有什么区别了。 而…...

IoT数据采集网关在企业应用中扮演着关键角色-天拓四方
随着物联网(IoT)技术的不断发展,越来越多的企业开始利用IoT技术实现智能化、自动化的生产和管理。在这个过程中,IoT数据采集网关作为连接物理世界与数字世界的桥梁,发挥着至关重要的作用。 IoT数据采集网关是一种硬件…...

【动态规划】完全背包
欢迎来到Cefler的博客😁 🕌博客主页:折纸花满衣 🏠个人专栏:题目解析 🌎推荐文章:【LeetCode】winter vacation training 目录 👉🏻完全背包 👉🏻…...

从零开始学习Diffusion Models: Sharon Zhou
How Diffusion Models Work 本文是 https://www.deeplearning.ai/short-courses/how-diffusion-models-work/ 这门课程的学习笔记。 文章目录 How Diffusion Models WorkWhat you’ll learn in this course [1] Intuition[2] SamplingSetting Things UpSamplingDemonstrate i…...
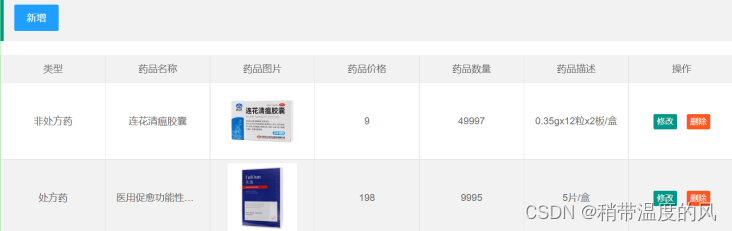
全天候购药系统(微信小程序+web后台管理)
PurchaseApplet 全天候购药系统(微信小程序web后台管理) 传统线下购药方式存在无法全天候向用户提供购药服务,无法随时提供诊疗服务等问题。为此,运用软件工程开发规范,充分调研建立需求模型,编写开发文档…...
)
L2-003 月饼(Java)
月饼是中国人在中秋佳节时吃的一种传统食品,不同地区有许多不同风味的月饼。现给定所有种类月饼的库存量、总售价、以及市场的最大需求量,请你计算可以获得的最大收益是多少。 注意:销售时允许取出一部分库存。样例给出的情形是这样的&#…...

vue面试--101, 1vue3为啥比vue2好 2 vue3为什么使用proxy
1vue3为啥比vue2好 2 vue3为什么使用proxy...
【sgPhotoPlayer】自定义组件:图片预览,支持点击放大、缩小、旋转图片
特性: 支持设置初始索引值支持显示标题、日期、大小、当前图片位置支持无限循环切换轮播支持鼠标滑轮滚动、左右键、上下键、PageUp、PageDown、Home、End操作切换图片支持Esc关闭窗口 sgPhotoPlayer源码 <template><div :class"$options.name"…...
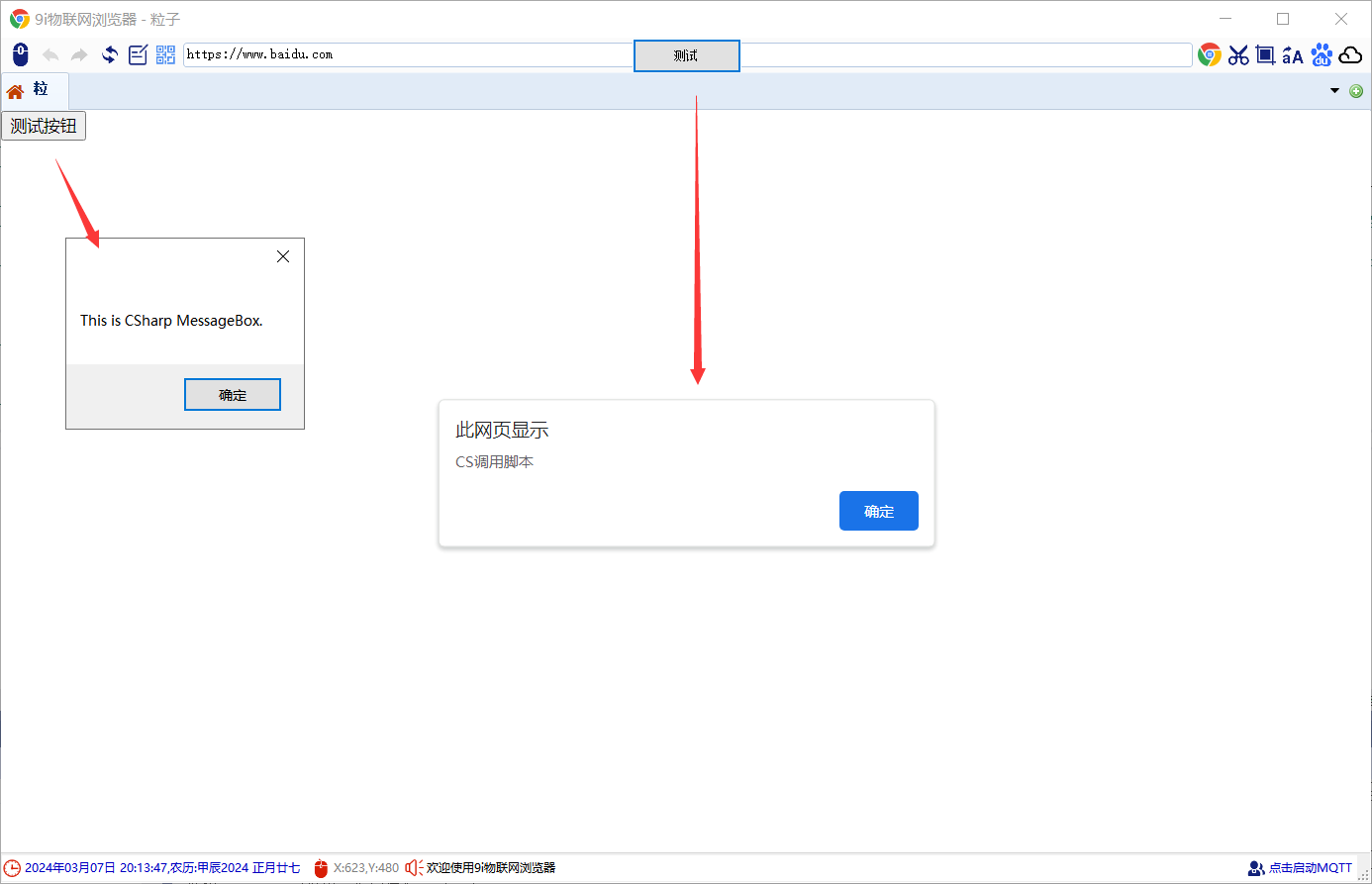
cefsharp(winForm)调用js脚本,js脚本调用c#方法
本博文针对js-csharp交互(相互调用的应用) (一)、js调用c#方法 1.1 类名称:cs_js_obj public class cs_js_obj{//注意,js调用C#,不一定在主线程上调用的,需要用SynchronizationContext来切换到主线程//private System.Threading.SynchronizationContext context;//…...
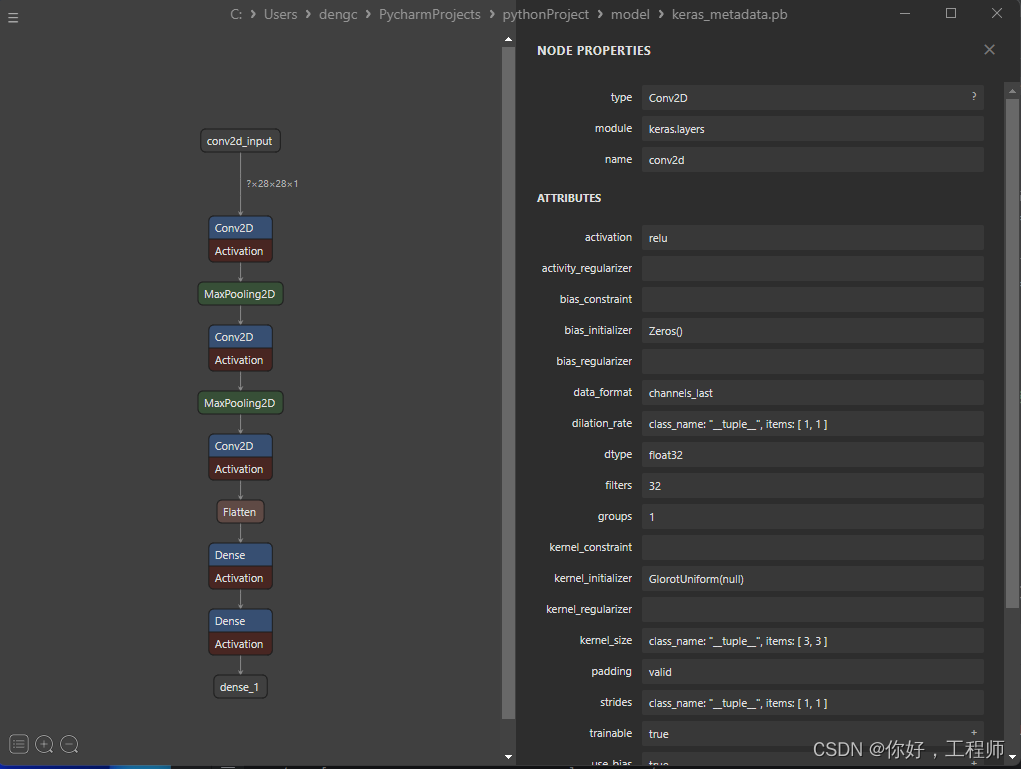
Tensorflow实现手写数字识别
模型架构 具有10个神经元,对应10个类别(0-9的数字)。使用softmax激活函数,对多分类问题进行概率归一化。输出层 (Dense):具有64个神经元。激活函数为ReLU。全连接层 (Dense):将二维数据展平成一维,为全连接层做准备。展…...

谈谈杭州某小公司面试的经历
#面试#本人bg211本,一段实习,前几天面了杭州某小厂公司,直接给我干无语了! 1、先介绍介绍你自己,我说了我的一个情况。 2、没获奖和竞赛经历吗?我说确实没有呢,面试官叹气了一下,只是…...
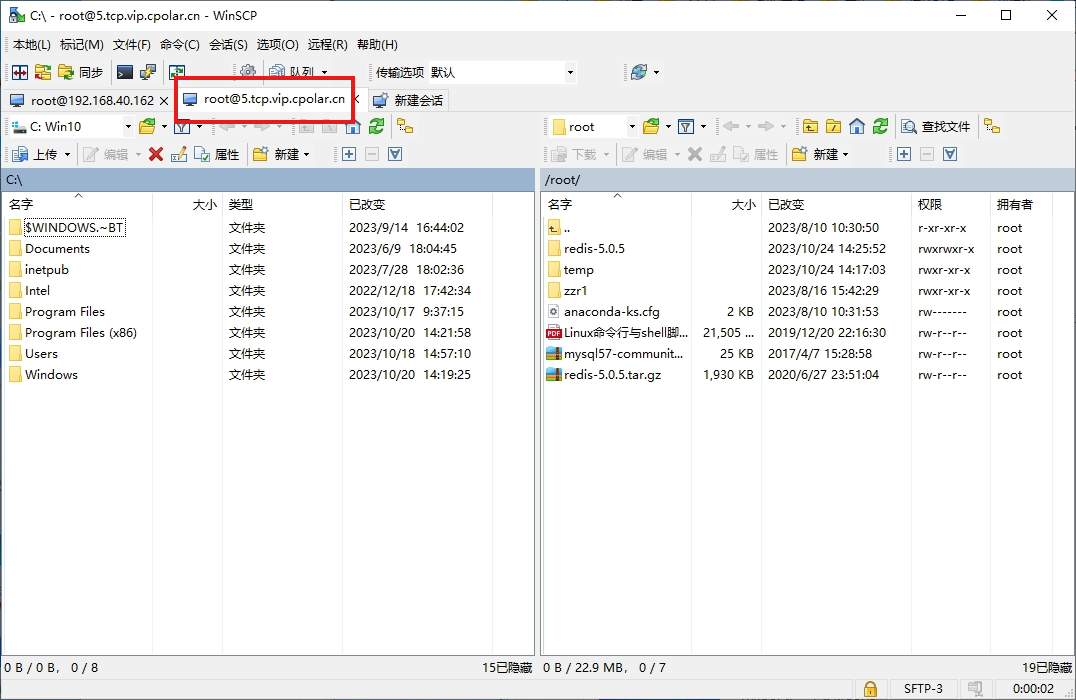
如何使用WinSCP结合Cpolar实现公网远程访问内网Linux服务器
文章目录 1. 简介2. 软件下载安装:3. SSH链接服务器4. WinSCP使用公网TCP地址链接本地服务器5. WinSCP使用固定公网TCP地址访问服务器 1. 简介 Winscp是一个支持SSH(Secure SHell)的可视化SCP(Secure Copy)文件传输软件,它的主要功能是在本地与远程计…...

6. 互质
互质 互质 互质 每次测试的时间限制: 3 秒 每次测试的时间限制:3 秒 每次测试的时间限制:3秒 每次测试的内存限制: 256 兆字节 每次测试的内存限制:256 兆字节 每次测试的内存限制:256兆字节 题目描述 给定…...

微信小程序(五十一)页面背景(全屏)
注释很详细,直接上代码 上一篇 新增内容: 1.页面背景的基本写法 2.去除默认上标题实习全屏背景 3. 背景适配细节 源码: index.wxss page{/* 背景链接 */background-image: url(https://pic3.zhimg.com/v2-a76bafdecdacebcc89b5d4f351a53e6a_…...
MATLAB | MATLAB版玫瑰祝伟大女性节日快乐!!
妇女节到了,这里祝全体伟大的女性,节日快乐,事业有成,万事胜意。 作为MATLAB爱好者,这里还是老传统画朵花叭,不过感觉大部分样式的花都画过了,这里将一段很古老的2012年的html玫瑰花代码转成MA…...
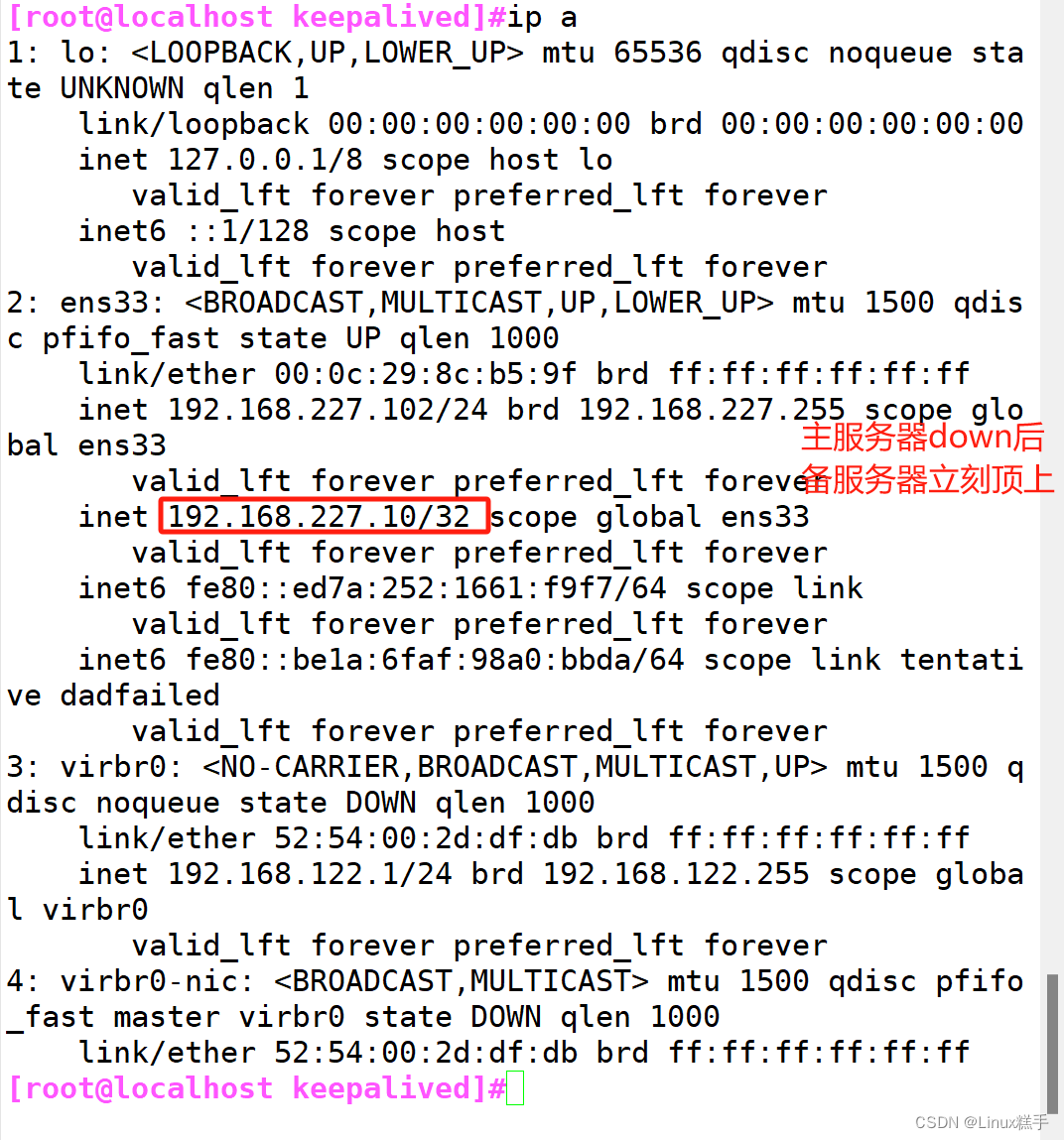
LVS+Keepalived 高可用集群
目录 一.Keepalived工具介绍 1.用户空间核心组件: (1)vrrp stack:VIP消息通告 (2)checkers:监测real server(简单来说 就是监控后端真实服务器的服务) (…...

Linux:kubernetes(k8s)探针ReadinessProbe的使用(9)
本章yaml文件是根据之前文章迭代修改过来的 先将之前的pod删除,然后使用下面这个yaml进行生成pod apiVersion: v1 # api文档版本 kind: Pod # 资源对象类型 metadata: # pod相关的元数据,用于描述pod的数据name: nginx-po # pod名称labels: # pod的标…...
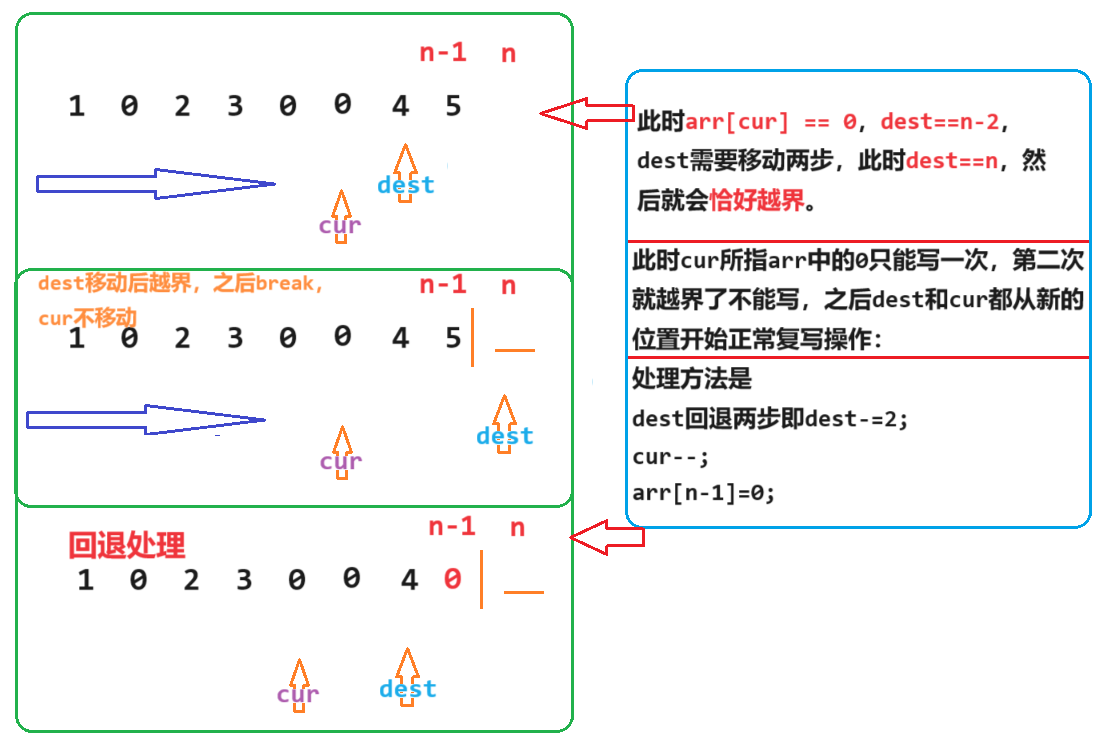
专题一 - 双指针 - leetcode 1089. 复写零 - 简单难度
leetcode 1089. 复写零 leetcode 1089. 复写零 | 简单难度1. 题目详情1. 原题链接2. 基础框架 2. 解题思路1. 题目分析2. 算法原理3. 时间复杂度 3. 代码实现4. 知识与收获 leetcode 1089. 复写零 | 简单难度 1. 题目详情 给你一个长度固定的整数数组 arr ,请你将…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...
与文本切分器(Splitter)详解《二》)
LangChain 中的文档加载器(Loader)与文本切分器(Splitter)详解《二》
🧠 LangChain 中 TextSplitter 的使用详解:从基础到进阶(附代码) 一、前言 在处理大规模文本数据时,特别是在构建知识库或进行大模型训练与推理时,文本切分(Text Splitting) 是一个…...

文件上传漏洞防御全攻略
要全面防范文件上传漏洞,需构建多层防御体系,结合技术验证、存储隔离与权限控制: 🔒 一、基础防护层 前端校验(仅辅助) 通过JavaScript限制文件后缀名(白名单)和大小,提…...

麒麟系统使用-进行.NET开发
文章目录 前言一、搭建dotnet环境1.获取相关资源2.配置dotnet 二、使用dotnet三、其他说明总结 前言 麒麟系统的内核是基于linux的,如果需要进行.NET开发,则需要安装特定的应用。由于NET Framework 是仅适用于 Windows 版本的 .NET,所以要进…...

【字节拥抱开源】字节团队开源视频模型 ContentV: 有限算力下的视频生成模型高效训练
本项目提出了ContentV框架,通过三项关键创新高效加速基于DiT的视频生成模型训练: 极简架构设计,最大化复用预训练图像生成模型进行视频合成系统化的多阶段训练策略,利用流匹配技术提升效率经济高效的人类反馈强化学习框架&#x…...
