【动态规划】完全背包

欢迎来到Cefler的博客😁
🕌博客主页:折纸花满衣
🏠个人专栏:题目解析
🌎推荐文章:【LeetCode】winter vacation training

目录
- 👉🏻完全背包
👉🏻完全背包
原题链接:完全背包
mycode1(超出时间限制):
#include <iostream>
#include<vector>
using namespace std;int main() {int n, V;cin >> n >> V;vector<int> w(n + 1), v(n + 1);// vector<vector<int>> goods(n,vector<int>(2));for (int k = 1; k <= n; k++) cin >> v[k] >> w[k];//创建dp表vector<vector<int>> dp1(n + 1, vector<int>(V + 1)), dp2(n + 1, vector<int>(V + 1));//dp表初始化for (int k = 1; k < V + 1; k++){dp2[0][k] = -1;}//开始填表for (int i = 1; i < n + 1; i++){for (int j = 1; j < V + 1; j++){// dp1[i][j]特征方程dp1[i][j] = dp1[i - 1][j];int num = 1;if (j - v[i] >= 0){dp1[i][j] = max(dp1[i][j], w[i] * num + dp1[i - 1][j - v[i] * num]);//一定要在这个位置先放一个,可能第一个就是最大(调试出来的血泪)for (; j - v[i] * num >= 0; num++){dp1[i][j] = max(dp1[i][j], w[i] * num + dp1[i - 1][j - v[i] * num]);}//--num;//因为此时j - v[i] * num已经<0所以此时要--num恢复j - v[i] * num >= 0的num状态//dp1[i][j] = max(dp1[i][j], w[i] * num + dp1[i - 1][j - v[i] * num]);}//dp2[i][j]特征方程num = 1;//num重新初始化为1dp2[i][j] = dp2[i - 1][j];if (j - v[i] >= 0 && dp2[i ][j - v[i]] != -1){dp2[i][j] = max(dp2[i][j], w[i] * num + dp2[i][j - v[i] * num]);//一定要在这个位置先放一个,可能第一个就是最大(调试出来的血泪)for (; j - v[i] * num >= 0 && dp2[i][j - v[i] * num] != -1; num++){dp2[i][j] = max(dp2[i][j], w[i] * num + dp2[i][j - v[i] * num]);}//--num;//因为此时j - v[i] * num已经<0所以此时要--num恢复j - v[i] * num >= 0的num状态//dp2[i][j] = max(dp2[i][j], w[i] * num + dp2[i][j - v[i] * num]);}}}cout << dp1[n][V] << endl;cout << (dp2[n][V] == -1 ? 0 : dp2[n][V]) << endl;
}
我好不容易心动一次,你却让我输得这么彻底~呵呵
优化代码:

这里主要优化了状态转移方程
mycode2:
#include <iostream>
#include<vector>
using namespace std;
int main() {int n, V;cin >> n >> V;vector<int> w(n + 1), v(n + 1);// vector<vector<int>> goods(n,vector<int>(2));for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];//创建dp表vector<vector<int>> dp1(n + 1, vector<int>(V + 1)), dp2(n + 1, vector<int>(V + 1));//dp表初始化for (int i = 1; i < V + 1; i++){dp2[0][i] = -1;}//开始填表for (int i = 1; i < n + 1; i++){for (int j = 0; j < V + 1; j++){//dp1[i][j]特征方程dp1[i][j] = dp1[i - 1][j];if (j - v[i] >= 0)dp1[i][j] = max(dp1[i][j], w[i] + dp1[i ][j - v[i]]);//dp2[i][j]特征方程dp2[i][j] = dp2[i - 1][j];if (j - v[i] >= 0 && dp2[i][j - v[i]] != -1)dp2[i][j] = max(dp2[i][j], w[i] + dp2[i][j - v[i]]);}}cout << dp1[n][V] << endl;cout << (dp2[n][V] == -1 ? 0 : dp2[n][V]) << endl;
}
相关文章:

【动态规划】完全背包
欢迎来到Cefler的博客😁 🕌博客主页:折纸花满衣 🏠个人专栏:题目解析 🌎推荐文章:【LeetCode】winter vacation training 目录 👉🏻完全背包 👉🏻…...

从零开始学习Diffusion Models: Sharon Zhou
How Diffusion Models Work 本文是 https://www.deeplearning.ai/short-courses/how-diffusion-models-work/ 这门课程的学习笔记。 文章目录 How Diffusion Models WorkWhat you’ll learn in this course [1] Intuition[2] SamplingSetting Things UpSamplingDemonstrate i…...
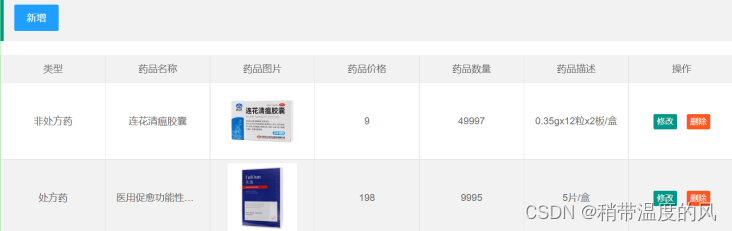
全天候购药系统(微信小程序+web后台管理)
PurchaseApplet 全天候购药系统(微信小程序web后台管理) 传统线下购药方式存在无法全天候向用户提供购药服务,无法随时提供诊疗服务等问题。为此,运用软件工程开发规范,充分调研建立需求模型,编写开发文档…...
)
L2-003 月饼(Java)
月饼是中国人在中秋佳节时吃的一种传统食品,不同地区有许多不同风味的月饼。现给定所有种类月饼的库存量、总售价、以及市场的最大需求量,请你计算可以获得的最大收益是多少。 注意:销售时允许取出一部分库存。样例给出的情形是这样的&#…...

vue面试--101, 1vue3为啥比vue2好 2 vue3为什么使用proxy
1vue3为啥比vue2好 2 vue3为什么使用proxy...
【sgPhotoPlayer】自定义组件:图片预览,支持点击放大、缩小、旋转图片
特性: 支持设置初始索引值支持显示标题、日期、大小、当前图片位置支持无限循环切换轮播支持鼠标滑轮滚动、左右键、上下键、PageUp、PageDown、Home、End操作切换图片支持Esc关闭窗口 sgPhotoPlayer源码 <template><div :class"$options.name"…...
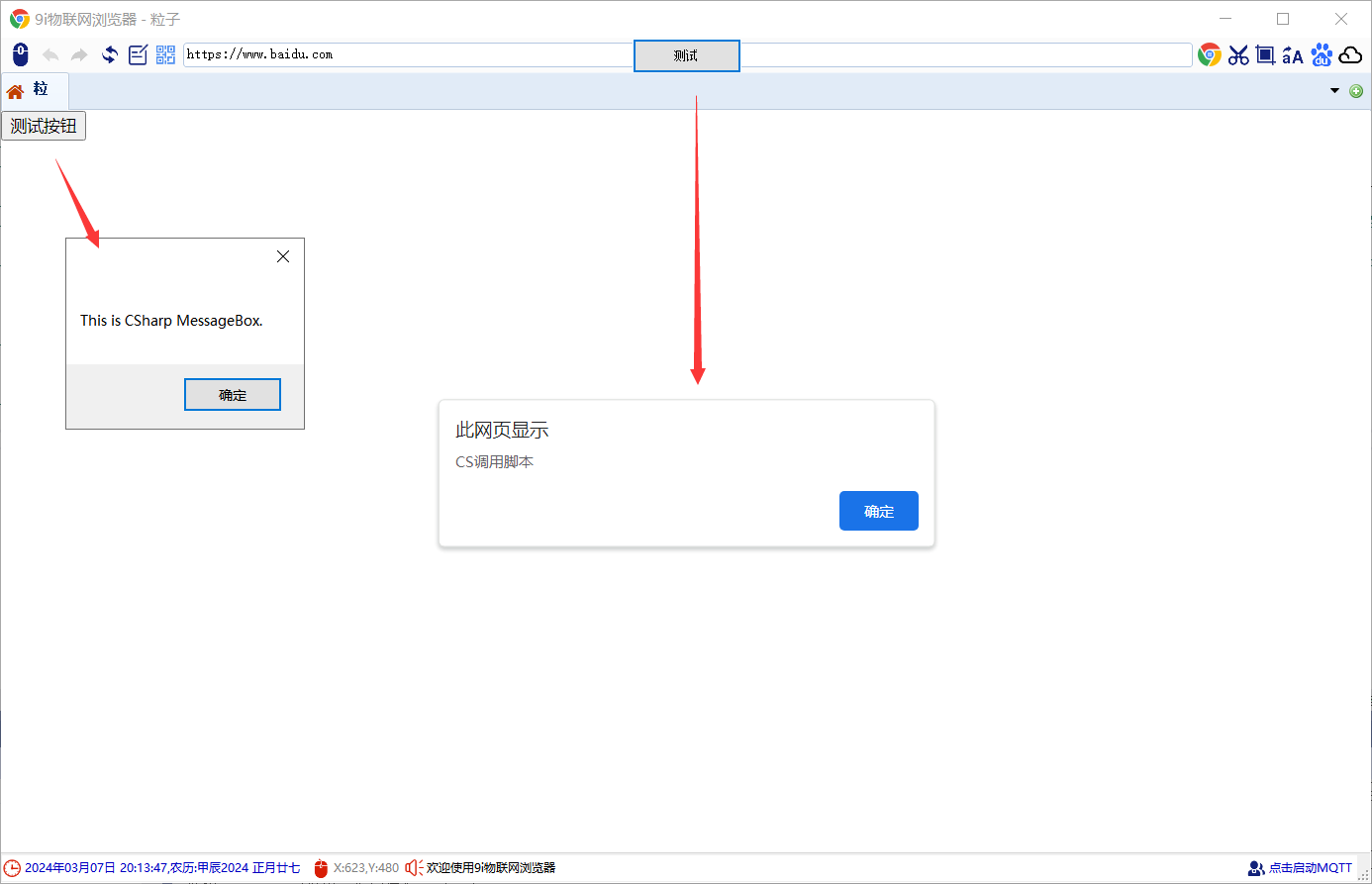
cefsharp(winForm)调用js脚本,js脚本调用c#方法
本博文针对js-csharp交互(相互调用的应用) (一)、js调用c#方法 1.1 类名称:cs_js_obj public class cs_js_obj{//注意,js调用C#,不一定在主线程上调用的,需要用SynchronizationContext来切换到主线程//private System.Threading.SynchronizationContext context;//…...
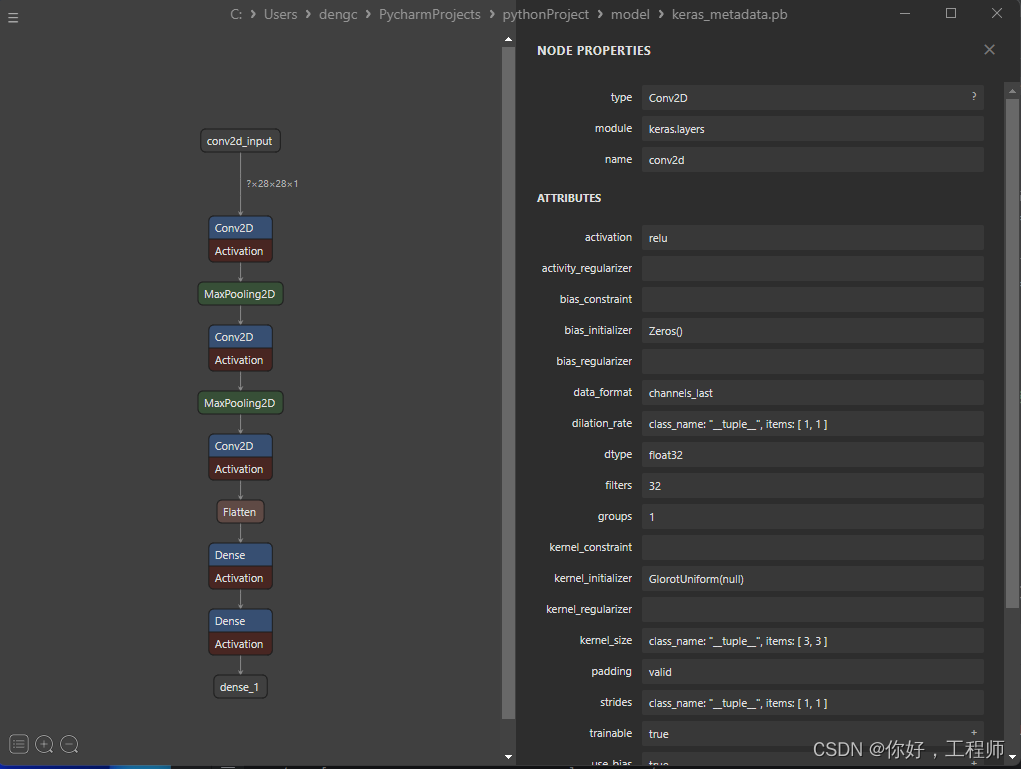
Tensorflow实现手写数字识别
模型架构 具有10个神经元,对应10个类别(0-9的数字)。使用softmax激活函数,对多分类问题进行概率归一化。输出层 (Dense):具有64个神经元。激活函数为ReLU。全连接层 (Dense):将二维数据展平成一维,为全连接层做准备。展…...

谈谈杭州某小公司面试的经历
#面试#本人bg211本,一段实习,前几天面了杭州某小厂公司,直接给我干无语了! 1、先介绍介绍你自己,我说了我的一个情况。 2、没获奖和竞赛经历吗?我说确实没有呢,面试官叹气了一下,只是…...
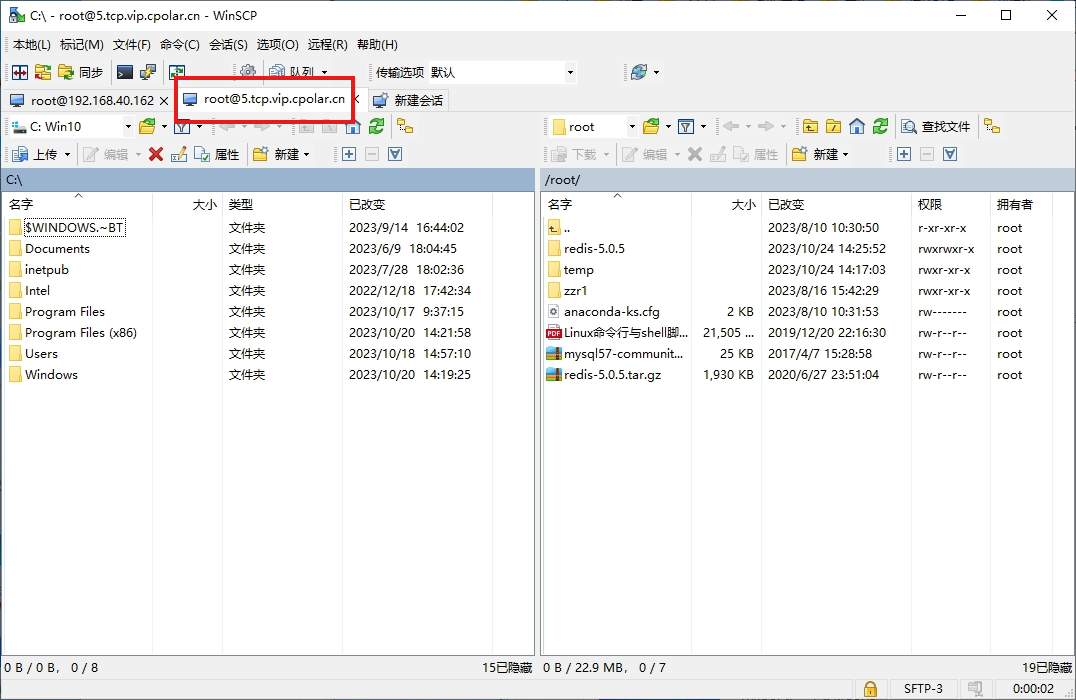
如何使用WinSCP结合Cpolar实现公网远程访问内网Linux服务器
文章目录 1. 简介2. 软件下载安装:3. SSH链接服务器4. WinSCP使用公网TCP地址链接本地服务器5. WinSCP使用固定公网TCP地址访问服务器 1. 简介 Winscp是一个支持SSH(Secure SHell)的可视化SCP(Secure Copy)文件传输软件,它的主要功能是在本地与远程计…...

6. 互质
互质 互质 互质 每次测试的时间限制: 3 秒 每次测试的时间限制:3 秒 每次测试的时间限制:3秒 每次测试的内存限制: 256 兆字节 每次测试的内存限制:256 兆字节 每次测试的内存限制:256兆字节 题目描述 给定…...

微信小程序(五十一)页面背景(全屏)
注释很详细,直接上代码 上一篇 新增内容: 1.页面背景的基本写法 2.去除默认上标题实习全屏背景 3. 背景适配细节 源码: index.wxss page{/* 背景链接 */background-image: url(https://pic3.zhimg.com/v2-a76bafdecdacebcc89b5d4f351a53e6a_…...
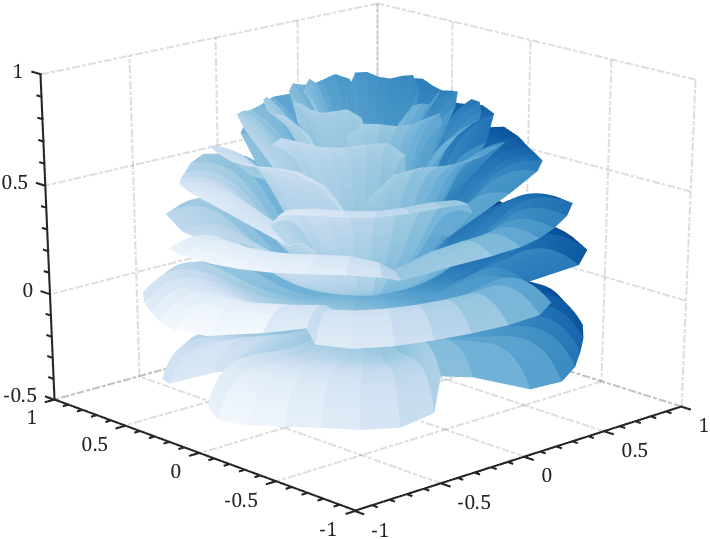
MATLAB | MATLAB版玫瑰祝伟大女性节日快乐!!
妇女节到了,这里祝全体伟大的女性,节日快乐,事业有成,万事胜意。 作为MATLAB爱好者,这里还是老传统画朵花叭,不过感觉大部分样式的花都画过了,这里将一段很古老的2012年的html玫瑰花代码转成MA…...
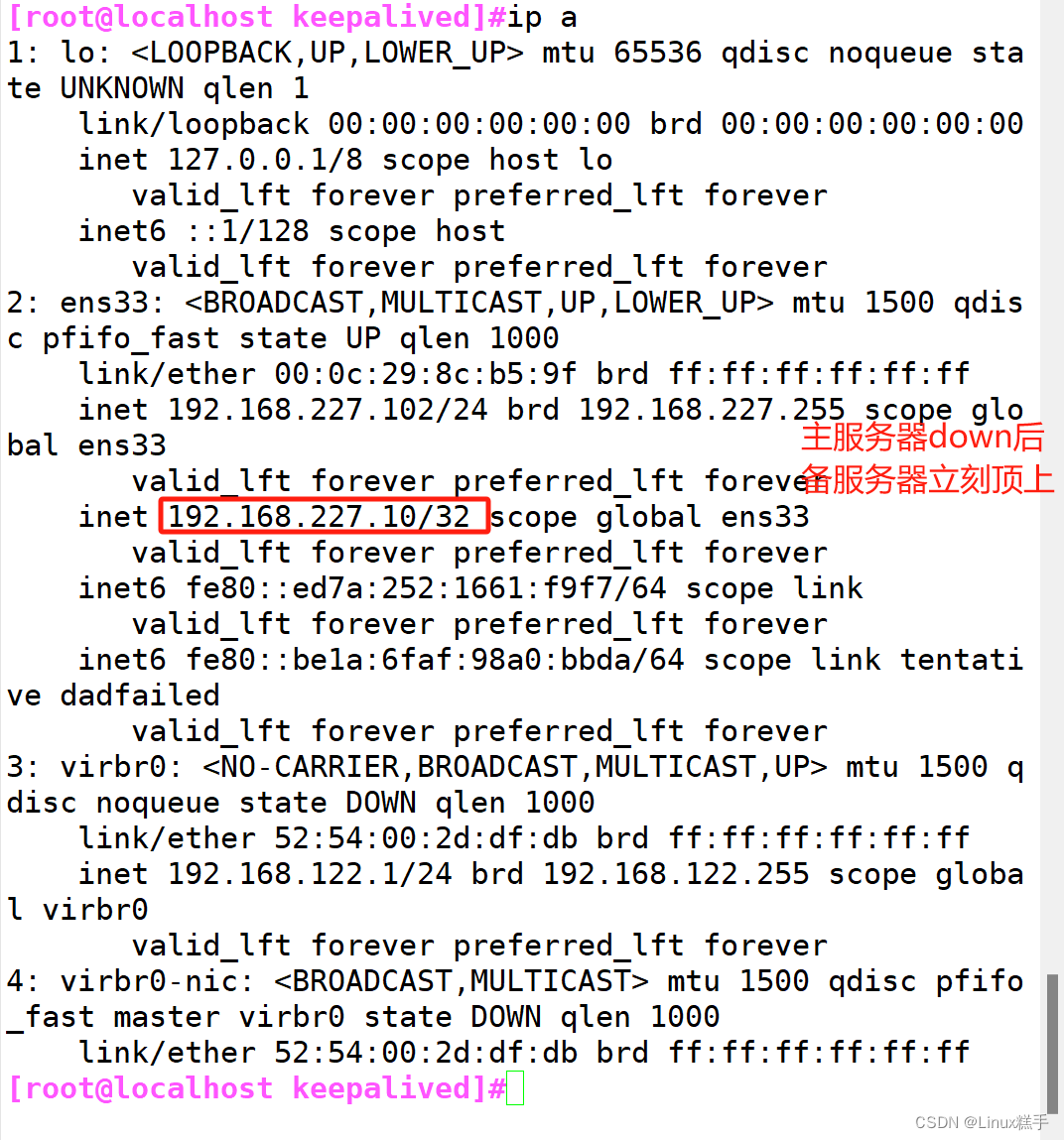
LVS+Keepalived 高可用集群
目录 一.Keepalived工具介绍 1.用户空间核心组件: (1)vrrp stack:VIP消息通告 (2)checkers:监测real server(简单来说 就是监控后端真实服务器的服务) (…...

Linux:kubernetes(k8s)探针ReadinessProbe的使用(9)
本章yaml文件是根据之前文章迭代修改过来的 先将之前的pod删除,然后使用下面这个yaml进行生成pod apiVersion: v1 # api文档版本 kind: Pod # 资源对象类型 metadata: # pod相关的元数据,用于描述pod的数据name: nginx-po # pod名称labels: # pod的标…...
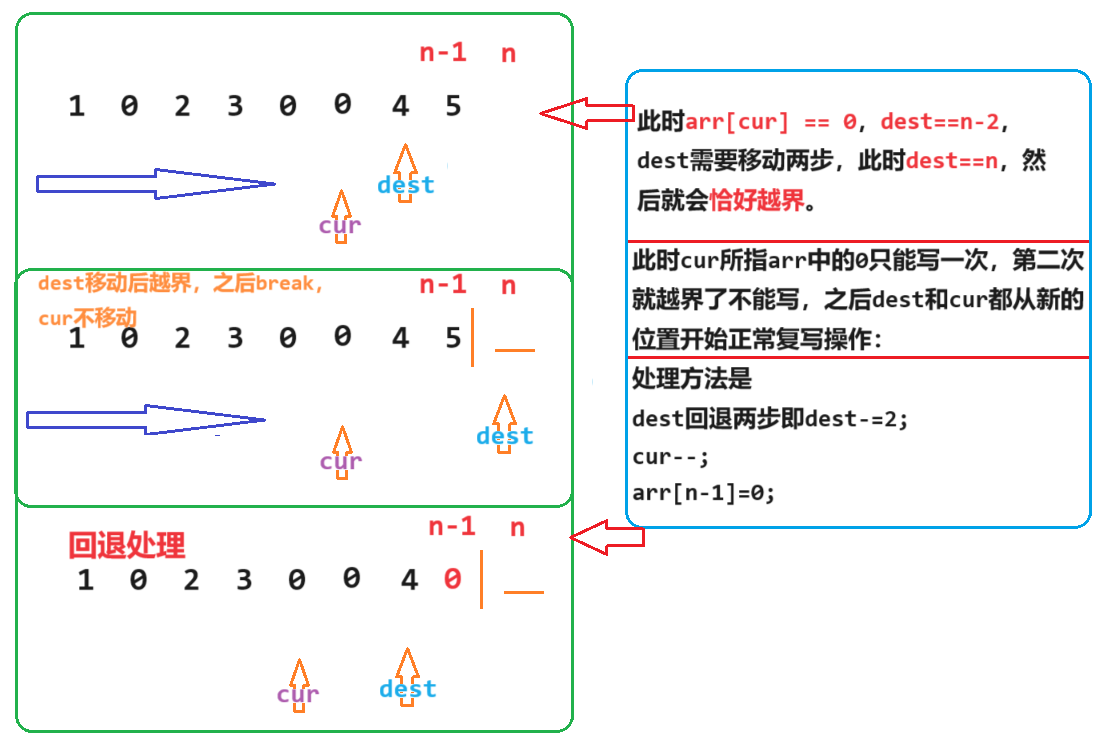
专题一 - 双指针 - leetcode 1089. 复写零 - 简单难度
leetcode 1089. 复写零 leetcode 1089. 复写零 | 简单难度1. 题目详情1. 原题链接2. 基础框架 2. 解题思路1. 题目分析2. 算法原理3. 时间复杂度 3. 代码实现4. 知识与收获 leetcode 1089. 复写零 | 简单难度 1. 题目详情 给你一个长度固定的整数数组 arr ,请你将…...
深入浅出(二)MVVM
MVVM 1. 简介2. 示例 1. 简介 2. 示例 示例下载地址:https://download.csdn.net/download/qq_43572400/88925141 创建C# WPF应用(.NET Framework)工程,WpfApp1 添加程序集 GalaSoft.MvvmLight 创建ViewModel文件夹,并创建MainWindowV…...
A题思路)
2023年第三届中国高校大数据挑战赛(第二场)A题思路
竞赛时间 (1)报名时间:即日起至2024年3月8日 (2)比赛时间:2024年3月9日8:00至2024年3月12日20:00 (3)成绩公布:2024年4月30日前 赛题方向:大数据统计分析 …...

数据挖掘:
一.数据仓库概述: 1.1数据仓库概述 1.1.1数据仓库定义 数据仓库是一个用于支持管理决策的、面向主题、集成、相对稳定且反映历史变化的数据集合。 1.1.2数据仓库四大特征 集成性(Integration): 数据仓库集成了来自多个不同来源…...

NDK,Jni
使用 NDK(Native Development Kit)意味着在 Android 应用程序中集成 C/C 代码。通常情况下,Android 应用程序主要使用 Java 或 Kotlin 编写,但有时候需要使用 C/C 来实现一些特定的功能或性能优化。 NDK 提供了一组工具和库&…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...
