Vue template到render过程
Vue template到render过程
- vue的模版编译过程主要如下:template -> ast -> render函数
- (1)调用parse方法将template转化为ast(抽象语法树)
- (2)对静态节点做优化
- (3)生成代码
vue的模版编译过程主要如下:template -> ast -> render函数
vue 在模版编译版本的码中会执行 compileToFunctions 将template转化为render函数:
// 将模板编译为render函数
const { render, staticRenderFns } = compileToFunctions(template,options, this)CompileToFunctions中的主要逻辑如下∶
(1)调用parse方法将template转化为ast(抽象语法树)
constast = parse(template.trim(), options)
parse的目标:把tamplate转换为AST树,它是一种用 JavaScript对象的形式来描述整个模板。
解析过程:利用正则表达式顺序解析模板,当解析到开始标签、闭合标签、文本的时候都会分别执行对应的 回调函数,来达到构造AST树的目的。
AST元素节点总共三种类型:type为1表示普通元素、2为表达式、3为纯文本
(2)对静态节点做优化
optimize(ast,options)
这个过程主要分析出哪些是静态节点,给其打一个标记,为后续更新渲染可以直接跳过静态节点做优化
深度遍历AST,查看每个子树的节点元素是否为静态节点或者静态节点根。如果为静态节点,他们生成的DOM永远不会改变,这对运行时模板更新起到了极大的优化作用。
(3)生成代码
const code = generate(ast, options)
generate将ast抽象语法树编译成 render字符串并将静态部分放到 staticRenderFns 中,最后通过 new Function(“render”) 生成render函数。
相关文章:

Vue template到render过程
Vue template到render过程 vue的模版编译过程主要如下:template -> ast -> render函数(1)调用parse方法将template转化为ast(抽象语法树)(2)对静态节点做优化(3)生…...

【你也能从零基础学会网站开发】Web建站之HTML+CSS入门篇 CSS常用属性
🚀 个人主页 极客小俊 ✍🏻 作者简介:web开发者、设计师、技术分享 🐋 希望大家多多支持, 我们一起学习和进步! 🏅 欢迎评论 ❤️点赞💬评论 📂收藏 📂加关注 CSS常用属性…...

Golang 写日志到文件
package mainimport ("log""os""time" )func main() {printLog("auto", "报警内容AA") }func printLog(filename string, content string) {t : time.Now().Format(time.DateOnly)file : filename "." t "…...
数字孪生10个技术栈:数据处理的六步骤,以获得可靠数据。
一、什么是数据处理 在数字孪生中,数据处理是指对采集到的实时或历史数据进行整理、清洗、分析和转化的过程。数据处理是数字孪生的基础,它将原始数据转化为有意义的信息,用于模型构建、仿真和决策支持。 数据处理是为了提高数据质量、整合数…...
之centos搭建jenkins)
运维随录实战(5)之centos搭建jenkins
一,搭建jenkins准备 下载安装jdk环境 -》版本 jdk11 下载安装maven环境 -》版本 maven 3.8.8 git -》版本 1.8.3.1 yum install git jenkins安装版本:2.414.3 下载地址:https://get.jenkins.io/war-stable/2.414.3/jenkins.war 注:jenkins版本与jdk版本有一定的对应关…...
css clip-path polygon属性实现直角梯形
2024.3.8今天我学习了如何用css实现直角梯形的效果, 效果: 具体实现原理: 一、需要三个div: 外面一个大的div,里面左右两个小的div 我们需要先把第一个div变成直角梯形: 大概是这样,设置好之…...
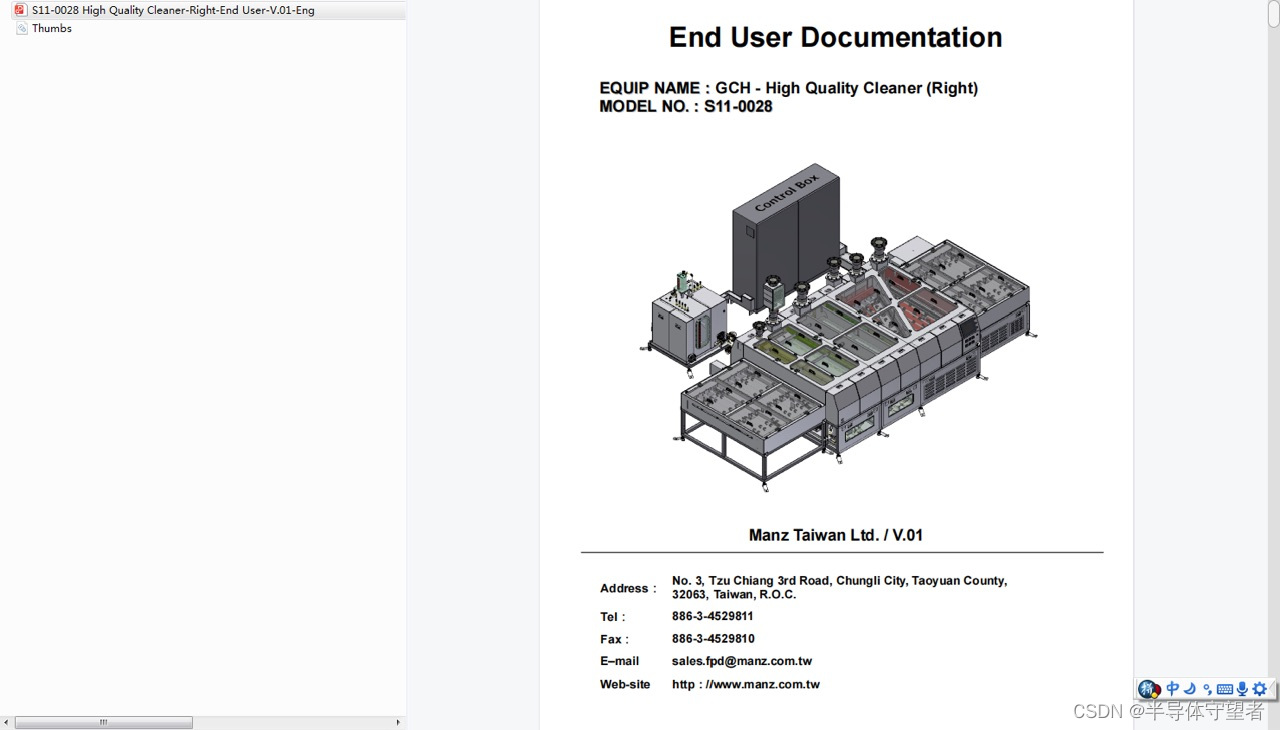
Manz高压清洗机S11-028GCH-High Quality Cleaner 操作使用说明492页
Manz高压清洗机S11-028GCH-High Quality Cleaner 操作使用说明492页...

图像处理与视觉感知---期末复习重点(2)
文章目录 一、空间域图像增强1.1 图像增强1.2 几种变换 二、直方图2.1 直方图定义2.2 直方图均衡化2.3 离散情况2.4 例子2.5 直方图匹配2.6 例子2.7 一道例题 三、空间滤波器3.1 定义3.2 例子 四、平滑空间滤波器4.1 作用与分类4.2 线性滤波器 五、统计排序滤波器5.1 定义与分类…...

【机器学习】三要素——数据、模型、算法
机器学习三要素 数据模型模型是怎么得到的?算法 我 在学习过程中,对于“模型”和“算法”的概念不清晰,一直混淆,通过查阅了一些资料在此总结一下。 数据、模型与算法被称为机器学习的三要素,因为它们在机器学习中具有不可分割的作…...
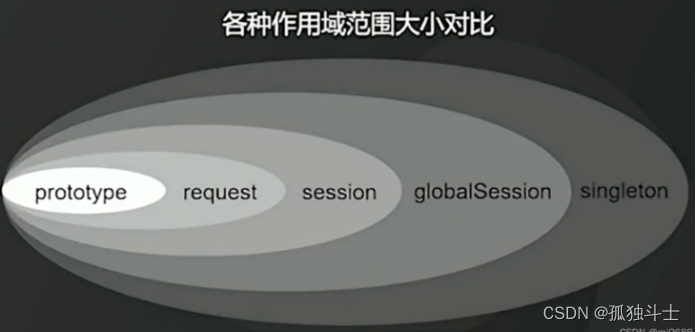
Spring框架Bean对象的五个作用域
一、前言:Bean对象简介 在Spring项目中,那些由Spring IoC容器所管理的对象,称为bean。简单地讲,bean就是由Spring容器初始化、装配及管理的对象,除此之外,bean就与应用程序中的其他对象没有什么区别了。 而…...

IoT数据采集网关在企业应用中扮演着关键角色-天拓四方
随着物联网(IoT)技术的不断发展,越来越多的企业开始利用IoT技术实现智能化、自动化的生产和管理。在这个过程中,IoT数据采集网关作为连接物理世界与数字世界的桥梁,发挥着至关重要的作用。 IoT数据采集网关是一种硬件…...

【动态规划】完全背包
欢迎来到Cefler的博客😁 🕌博客主页:折纸花满衣 🏠个人专栏:题目解析 🌎推荐文章:【LeetCode】winter vacation training 目录 👉🏻完全背包 👉🏻…...

从零开始学习Diffusion Models: Sharon Zhou
How Diffusion Models Work 本文是 https://www.deeplearning.ai/short-courses/how-diffusion-models-work/ 这门课程的学习笔记。 文章目录 How Diffusion Models WorkWhat you’ll learn in this course [1] Intuition[2] SamplingSetting Things UpSamplingDemonstrate i…...
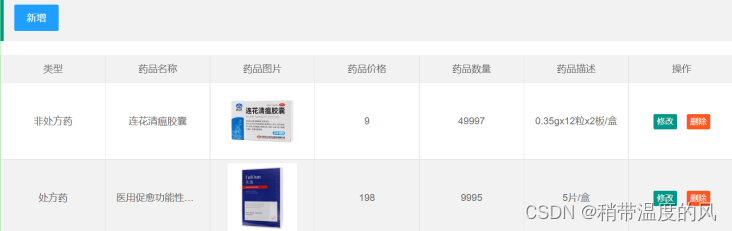
全天候购药系统(微信小程序+web后台管理)
PurchaseApplet 全天候购药系统(微信小程序web后台管理) 传统线下购药方式存在无法全天候向用户提供购药服务,无法随时提供诊疗服务等问题。为此,运用软件工程开发规范,充分调研建立需求模型,编写开发文档…...
)
L2-003 月饼(Java)
月饼是中国人在中秋佳节时吃的一种传统食品,不同地区有许多不同风味的月饼。现给定所有种类月饼的库存量、总售价、以及市场的最大需求量,请你计算可以获得的最大收益是多少。 注意:销售时允许取出一部分库存。样例给出的情形是这样的&#…...

vue面试--101, 1vue3为啥比vue2好 2 vue3为什么使用proxy
1vue3为啥比vue2好 2 vue3为什么使用proxy...
【sgPhotoPlayer】自定义组件:图片预览,支持点击放大、缩小、旋转图片
特性: 支持设置初始索引值支持显示标题、日期、大小、当前图片位置支持无限循环切换轮播支持鼠标滑轮滚动、左右键、上下键、PageUp、PageDown、Home、End操作切换图片支持Esc关闭窗口 sgPhotoPlayer源码 <template><div :class"$options.name"…...
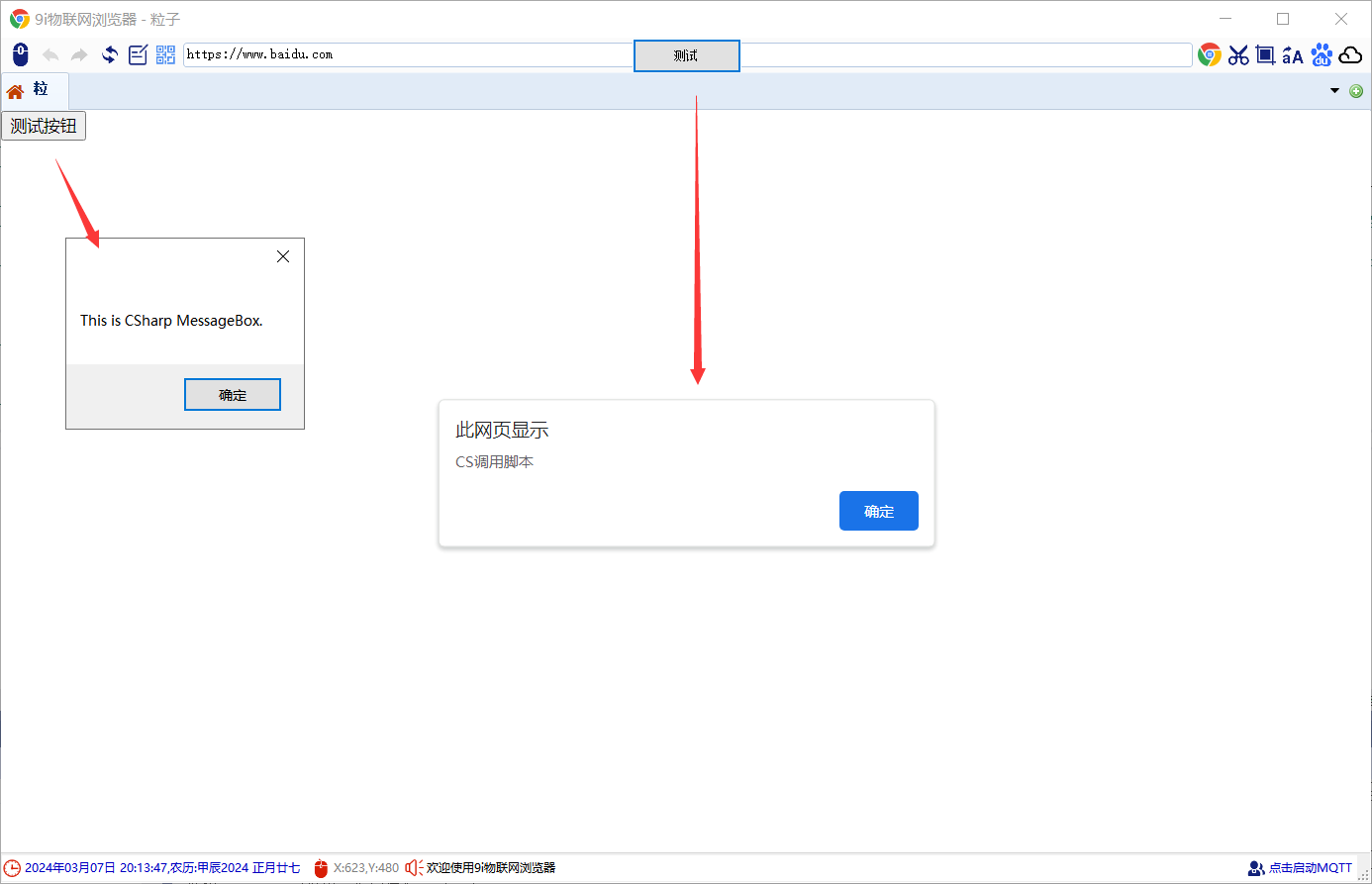
cefsharp(winForm)调用js脚本,js脚本调用c#方法
本博文针对js-csharp交互(相互调用的应用) (一)、js调用c#方法 1.1 类名称:cs_js_obj public class cs_js_obj{//注意,js调用C#,不一定在主线程上调用的,需要用SynchronizationContext来切换到主线程//private System.Threading.SynchronizationContext context;//…...
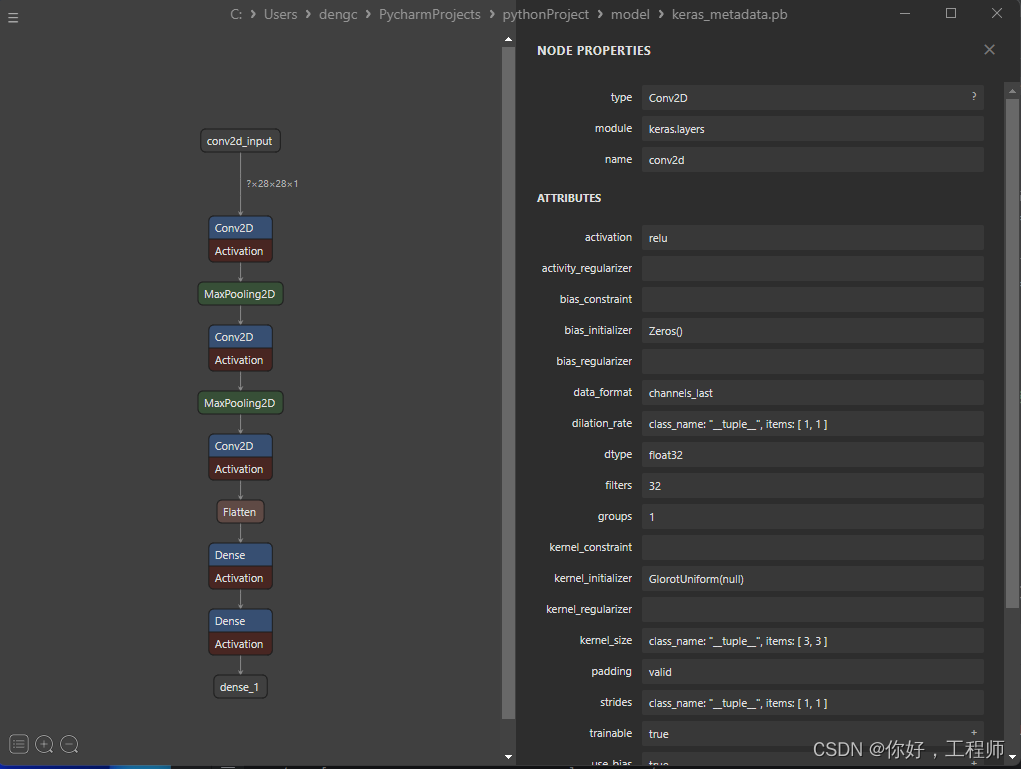
Tensorflow实现手写数字识别
模型架构 具有10个神经元,对应10个类别(0-9的数字)。使用softmax激活函数,对多分类问题进行概率归一化。输出层 (Dense):具有64个神经元。激活函数为ReLU。全连接层 (Dense):将二维数据展平成一维,为全连接层做准备。展…...

谈谈杭州某小公司面试的经历
#面试#本人bg211本,一段实习,前几天面了杭州某小厂公司,直接给我干无语了! 1、先介绍介绍你自己,我说了我的一个情况。 2、没获奖和竞赛经历吗?我说确实没有呢,面试官叹气了一下,只是…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...
