【深度优先】【图论】【C++算法】2045. 到达目的地的第二短时间
作者推荐
视频算法专题
LeetCode2045. 到达目的地的第二短时间
城市用一个 双向连通 图表示,图中有 n 个节点,从 1 到 n 编号(包含 1 和 n)。图中的边用一个二维整数数组 edges 表示,其中每个 edges[i] = [ui, vi] 表示一条节点 ui 和节点 vi 之间的双向连通边。每组节点对由 最多一条 边连通,顶点不存在连接到自身的边。穿过任意一条边的时间是 time 分钟。
每个节点都有一个交通信号灯,每 change 分钟改变一次,从绿色变成红色,再由红色变成绿色,循环往复。所有信号灯都 同时 改变。你可以在 任何时候 进入某个节点,但是 只能 在节点 信号灯是绿色时 才能离开。如果信号灯是 绿色 ,你 不能 在节点等待,必须离开。
第二小的值 是 严格大于 最小值的所有值中最小的值。
例如,[2, 3, 4] 中第二小的值是 3 ,而 [2, 2, 4] 中第二小的值是 4 。
给你 n、edges、time 和 change ,返回从节点 1 到节点 n 需要的 第二短时间 。
注意:
你可以 任意次 穿过任意顶点,包括 1 和 n 。
你可以假设在 启程时 ,所有信号灯刚刚变成 绿色 。
示例 1:
输入:n = 5, edges = [[1,2],[1,3],[1,4],[3,4],[4,5]], time = 3, change = 5
输出:13

解释:
上面的左图展现了给出的城市交通图。
右图中的蓝色路径是最短时间路径。
花费的时间是:
- 从节点 1 开始,总花费时间=0
- 1 -> 4:3 分钟,总花费时间=3
- 4 -> 5:3 分钟,总花费时间=6
因此需要的最小时间是 6 分钟。
右图中的红色路径是第二短时间路径。 - 从节点 1 开始,总花费时间=0
- 1 -> 3:3 分钟,总花费时间=3
- 3 -> 4:3 分钟,总花费时间=6
- 在节点 4 等待 4 分钟,总花费时间=10
- 4 -> 5:3 分钟,总花费时间=13
因此第二短时间是 13 分钟。
示例 2:
输入:n = 2, edges = [[1,2]], time = 3, change = 2
输出:11
解释:
最短时间路径是 1 -> 2 ,总花费时间 = 3 分钟
第二短时间路径是 1 -> 2 -> 1 -> 2 ,总花费时间 = 11 分钟
提示:
2 <= n <= 104
n - 1 <= edges.length <= min(2 * 104, n * (n - 1) / 2)
edges[i].length == 2
1 <= ui, vi <= n
ui != vi
不含重复边
每个节点都可以从其他节点直接或者间接到达
1 <= time, change <= 103
深度优先
经过的边数相同,则行驶时间相同,等待时间也相同。所以本题等效与求严格经过边数第二少。令经过最少的边数是x,则严格第二少的边数只能是x+1或x+2。因为:到达目的地后返回一个节点,再到达目的地,经过的边数是x+2。
本问题等于与:
一,计算最少经过边数x。
二,能否经过x+1条边到达目的的。
每个节点除了记录最少边数,还要记录另外一个状态i1:
初始为0,第一次到达是变成1。加入队列。
1变2的条件:新经过的边数等于x+1。加入队列。
2不会发生的变化。
每个节点最多入队两次。估计时间复杂度是:O(n)。
目的地的i1,如果为1,则严格第二少的边数为x+1,否则为x+2。
通过边数计算时间:
如果总时间time / change 是奇数需要等待 等待时间 change - (time/change)。
代码
核心代码
class CNeiBo2
{
public:CNeiBo2(int n, bool bDirect, int iBase = 0) :m_iN(n), m_bDirect(bDirect), m_iBase(iBase){m_vNeiB.resize(n);}CNeiBo2(int n, vector<vector<int>>& edges, bool bDirect, int iBase = 0) :m_iN(n), m_bDirect(bDirect), m_iBase(iBase){m_vNeiB.resize(n);for (const auto& v : edges){m_vNeiB[v[0] - iBase].emplace_back(v[1] - iBase);if (!bDirect){m_vNeiB[v[1] - iBase].emplace_back(v[0] - iBase);}}}inline void Add(int iNode1, int iNode2){iNode1 -= m_iBase;iNode2 -= m_iBase;m_vNeiB[iNode1].emplace_back(iNode2);if (!m_bDirect){m_vNeiB[iNode2].emplace_back(iNode1);}}const int m_iN;const bool m_bDirect;const int m_iBase;vector<vector<int>> m_vNeiB;
};class Solution {
public:int secondMinimum(int n, vector<vector<int>>& edges, int time, int change) {CNeiBo2 neiBo(n, edges, false, 1);queue<pair<int,int>> que; vector<int> vDis(n), vStatu(n);que.emplace(0,0);vStatu[0] = 1;while (que.size()){const auto [cur,curDis] = que.front();que.pop();for (const auto& next : neiBo.m_vNeiB[cur]){const int iNewDis = curDis + 1;if (0 == vStatu[next]){vDis[next] = iNewDis;vStatu[next] = 1;que.emplace(next,iNewDis);}else if ((1 == vStatu[next])&&( vDis[next]+1 == iNewDis)){vStatu[next] = 2;que.emplace(next, iNewDis);}}}const int iEdgeNum = (1 == vStatu.back()) ? (vDis.back() + 2) : (vDis.back() + 1);int iTime = 0;for (int i = 1; i <= iEdgeNum; i++){iTime += time;if ((iTime / change) & 1){if (iEdgeNum != i){iTime += (change - (iTime % change));}}}return iTime;}
};
测试用例
template<class T,class T2>
void Assert(const T& t1, const T2& t2)
{
assert(t1 == t2);
}
template
void Assert(const vector& v1, const vector& v2)
{
if (v1.size() != v2.size())
{
assert(false);
return;
}
for (int i = 0; i < v1.size(); i++)
{
Assert(v1[i], v2[i]);
}
}
int main()
{
int n, time, change;
vector<vector> edges;
{
Solution sln;
n = 5, edges = { {1,2},{1,3},{1,4},{3,4},{4,5} }, time = 3, change = 5;
auto res = sln.secondMinimum(n, edges, time, change);
Assert(13, res);
}
{
Solution sln;
n = 2, edges = { {1,2} }, time = 3, change = 2;
auto res = sln.secondMinimum(n, edges, time, change);
Assert(11, res);
}
}
2023年4月
class Solution {
public:
int secondMinimum(int n, vector<vector>& edges, int time, int change) {
m_vNeiB.resize(n + 1);
m_vDis.assign(n + 1,INT_MAX);
m_vDis2.assign(n + 1, INT_MAX);
for (const auto& e : edges)
{
m_vNeiB[e[0]].emplace_back(e[1]);
m_vNeiB[e[1]].emplace_back(e[0]);
}
std::queue<pair<int,int>> que;
que.emplace(1,0);
while (que.size())
{
const int iCur = que.front().first;
const int len = que.front().second;
que.pop();
for (const auto& next : m_vNeiB[iCur])
{
const int iNewLen = len + 1;
if (iNewLen >= m_vDis2[next])
{
continue;
}
que.emplace(next, iNewLen);
if (iNewLen < m_vDis[next])
{
m_vDis[next] = iNewLen;
}
else if (iNewLen != m_vDis[next])
{
m_vDis2[next] = iNewLen;
}
}
}
int tmp = m_vDis2[n];
int iRet = 0;
while (tmp–)
{
if ((iRet / change) & 1)
{
iRet += (change - iRet%change);
}
iRet += time;
}
return iRet;
}
vector<vector> m_vNeiB;
vector m_vDis;
vector m_vDis2;
};

扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快
速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关
下载
想高屋建瓴的学习算法,请下载《喜缺全书算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 我想对大家说的话 |
|---|
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法用**C++**实现。

相关文章:

【深度优先】【图论】【C++算法】2045. 到达目的地的第二短时间
作者推荐 视频算法专题 LeetCode2045. 到达目的地的第二短时间 城市用一个 双向连通 图表示,图中有 n 个节点,从 1 到 n 编号(包含 1 和 n)。图中的边用一个二维整数数组 edges 表示,其中每个 edges[i] [ui, vi] 表…...

思维题(蓝桥杯 填空题 C++)
目录 题目一: 编辑 代码: 题目二: 代码: 题目三: 代码: 题目四: 代码: 题目五: 代码: 题目六: 代码七: 题目八&#x…...

Meta的Llama2模型已上线!但我为何更推荐你从HuggingFace获取?还有Code Llama等你来解锁!
嘿,朋友们,今天给你们介绍一个新东西——Llama2模型,这是Meta(对,就是Facebook那家)推出的。 你可以直接去Llama的官网下载这个模型,然后按照他们GitHub上的指南来调用。 不过呢,我…...
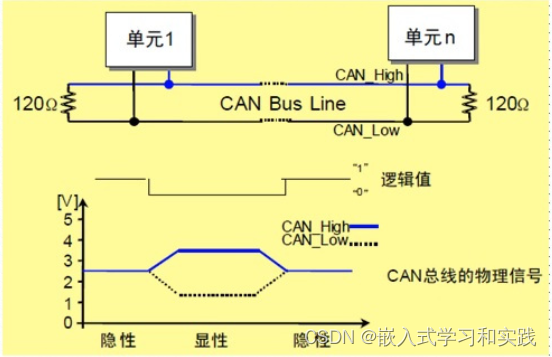
CAN总线及通讯的工作原理
一、CAN总线 CAN是控制器局域网络(Controller Area Network)的简称, 它是由研发和生产汽车电子产品著称的德国BOSCH公司开发的, 并最终成为国际标准(ISO11519),是国际上应用最广泛的现场总线之一。 二、工作原理 …...

linux下修改网卡MAC地址
我建议你使用 macchanger,但如果你不想使用它,那么可以使用另一种方法在 Linux 中更改 MAC 地址。 首先,使用以下命令关闭网卡: sudo ip link set dev enp0s31f6 down 接下来,使用以下命令设置新的 MAC:…...
47、WEB攻防——通用漏洞Java反序列化EXP生成数据提取组件安全
文章目录 序列化和反序列化的概念: 序列化:把java对象转换成字节流的过程;反序列化:把字节流恢复为java对象的过程。 对象的序列化主要有两种用途: 把对象的字节流永久的保存在硬盘上,通常存放在一个文件…...
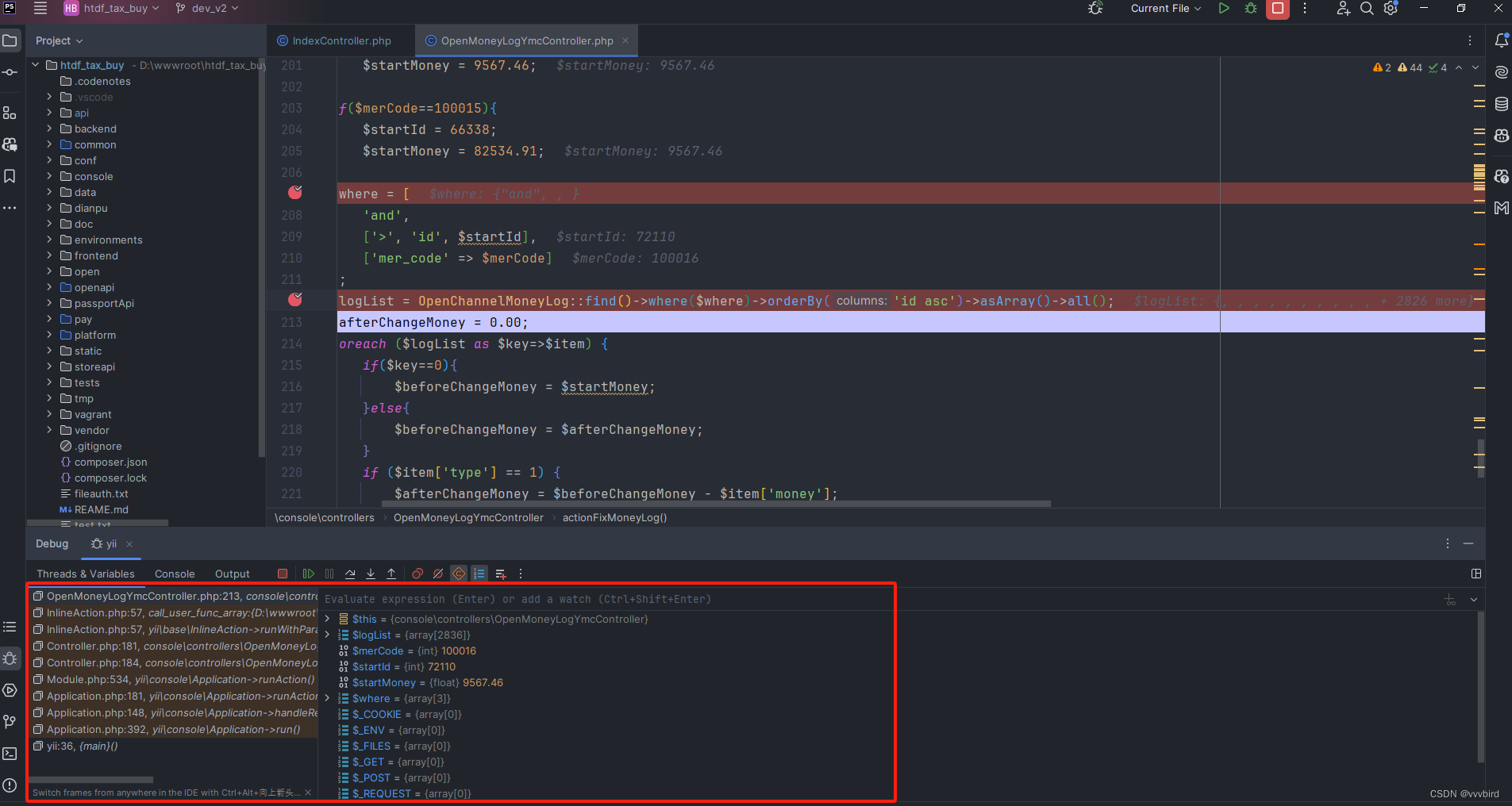
phpstorm console xdebug
1.所有配置跟浏览器http请求一样 2.记得Current File 必须是controller文件 注意:如果没有出发断点,则echo phpinfo(),查看remote_port 和phpstorm 配置是否对上。...

Vue template到render过程
Vue template到render过程 vue的模版编译过程主要如下:template -> ast -> render函数(1)调用parse方法将template转化为ast(抽象语法树)(2)对静态节点做优化(3)生…...

【你也能从零基础学会网站开发】Web建站之HTML+CSS入门篇 CSS常用属性
🚀 个人主页 极客小俊 ✍🏻 作者简介:web开发者、设计师、技术分享 🐋 希望大家多多支持, 我们一起学习和进步! 🏅 欢迎评论 ❤️点赞💬评论 📂收藏 📂加关注 CSS常用属性…...

Golang 写日志到文件
package mainimport ("log""os""time" )func main() {printLog("auto", "报警内容AA") }func printLog(filename string, content string) {t : time.Now().Format(time.DateOnly)file : filename "." t "…...
数字孪生10个技术栈:数据处理的六步骤,以获得可靠数据。
一、什么是数据处理 在数字孪生中,数据处理是指对采集到的实时或历史数据进行整理、清洗、分析和转化的过程。数据处理是数字孪生的基础,它将原始数据转化为有意义的信息,用于模型构建、仿真和决策支持。 数据处理是为了提高数据质量、整合数…...
之centos搭建jenkins)
运维随录实战(5)之centos搭建jenkins
一,搭建jenkins准备 下载安装jdk环境 -》版本 jdk11 下载安装maven环境 -》版本 maven 3.8.8 git -》版本 1.8.3.1 yum install git jenkins安装版本:2.414.3 下载地址:https://get.jenkins.io/war-stable/2.414.3/jenkins.war 注:jenkins版本与jdk版本有一定的对应关…...
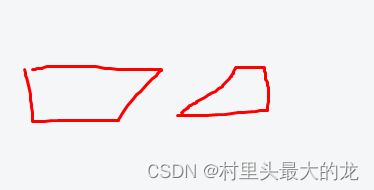
css clip-path polygon属性实现直角梯形
2024.3.8今天我学习了如何用css实现直角梯形的效果, 效果: 具体实现原理: 一、需要三个div: 外面一个大的div,里面左右两个小的div 我们需要先把第一个div变成直角梯形: 大概是这样,设置好之…...
Manz高压清洗机S11-028GCH-High Quality Cleaner 操作使用说明492页
Manz高压清洗机S11-028GCH-High Quality Cleaner 操作使用说明492页...

图像处理与视觉感知---期末复习重点(2)
文章目录 一、空间域图像增强1.1 图像增强1.2 几种变换 二、直方图2.1 直方图定义2.2 直方图均衡化2.3 离散情况2.4 例子2.5 直方图匹配2.6 例子2.7 一道例题 三、空间滤波器3.1 定义3.2 例子 四、平滑空间滤波器4.1 作用与分类4.2 线性滤波器 五、统计排序滤波器5.1 定义与分类…...

【机器学习】三要素——数据、模型、算法
机器学习三要素 数据模型模型是怎么得到的?算法 我 在学习过程中,对于“模型”和“算法”的概念不清晰,一直混淆,通过查阅了一些资料在此总结一下。 数据、模型与算法被称为机器学习的三要素,因为它们在机器学习中具有不可分割的作…...
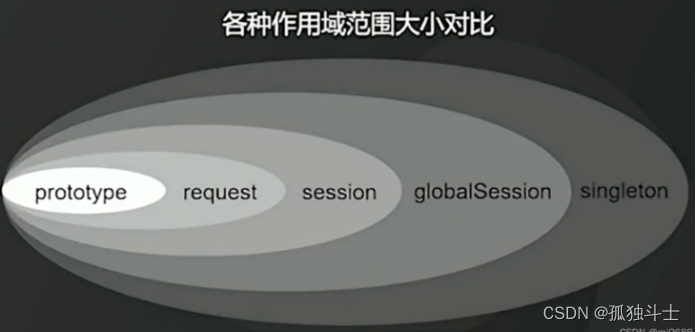
Spring框架Bean对象的五个作用域
一、前言:Bean对象简介 在Spring项目中,那些由Spring IoC容器所管理的对象,称为bean。简单地讲,bean就是由Spring容器初始化、装配及管理的对象,除此之外,bean就与应用程序中的其他对象没有什么区别了。 而…...

IoT数据采集网关在企业应用中扮演着关键角色-天拓四方
随着物联网(IoT)技术的不断发展,越来越多的企业开始利用IoT技术实现智能化、自动化的生产和管理。在这个过程中,IoT数据采集网关作为连接物理世界与数字世界的桥梁,发挥着至关重要的作用。 IoT数据采集网关是一种硬件…...

【动态规划】完全背包
欢迎来到Cefler的博客😁 🕌博客主页:折纸花满衣 🏠个人专栏:题目解析 🌎推荐文章:【LeetCode】winter vacation training 目录 👉🏻完全背包 👉🏻…...

从零开始学习Diffusion Models: Sharon Zhou
How Diffusion Models Work 本文是 https://www.deeplearning.ai/short-courses/how-diffusion-models-work/ 这门课程的学习笔记。 文章目录 How Diffusion Models WorkWhat you’ll learn in this course [1] Intuition[2] SamplingSetting Things UpSamplingDemonstrate i…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...
