常见的验证码
一、短信验证码
前端:
- 用户填写手机号,点击按钮发送请求
- 用户短信得到验证码后,用户填写表单
- 提交 form 表单,进行验证
后台:
- 随机生成几位验证码
- 并将生成时间、手机号、验证码存储起来,可以存到session、redis、数据库等
- 调用短信接口提供的sdk短信发送接口,将验证码发送到指定的手机号上
参考链接
二、图形验证码
前端:
- 用户填写手机号,在 input 框失去焦点时,发送获取验证码请求
- 得到后台的 base64 编码,并显示出来
<img src={`data:;base64,${verifyCodeUrl}`} onClick={handleGetVerifyCode} />
- 提交 form 表单,进行验证
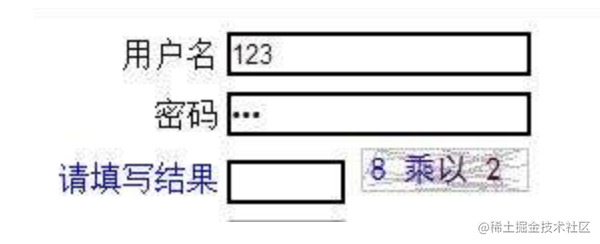
但是它不安全,脚本可以高准确率、快速地识别出答案
类似的还有算数验证码
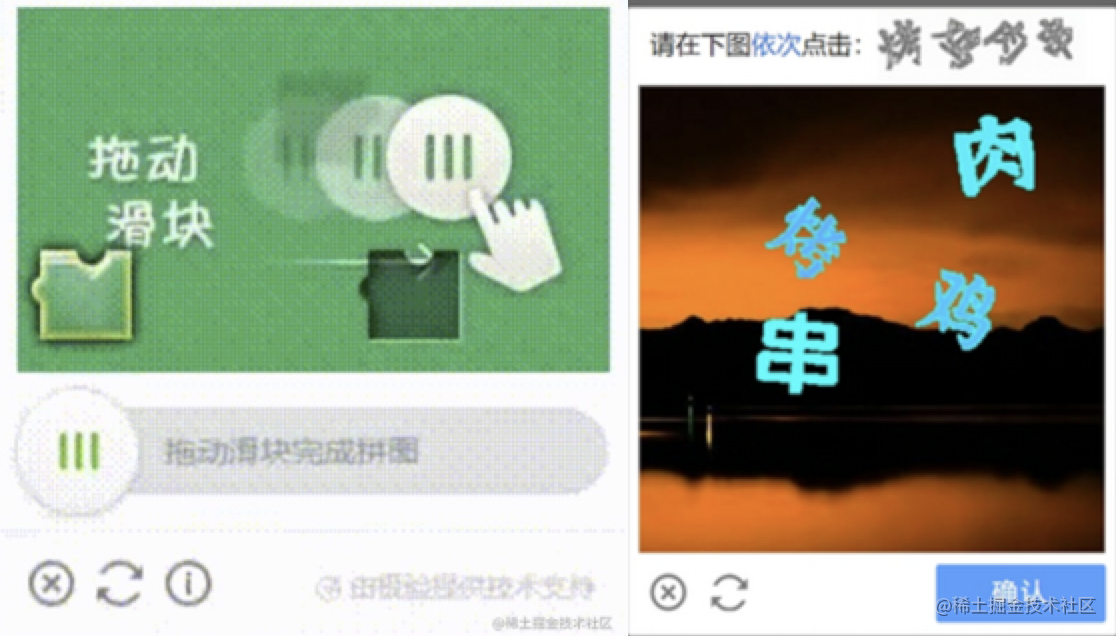
三、滑动拼图验证码
根据用户滑动滑块的响应时间,拖拽速度,时间,位置,轨迹,重试次数等验证,相对来说更安全。
- 有三张图,带缺口的背景图、拼图、完整的背景图
- 操作:
用户的操作:按住滑块,拖动图片至阴影位置,完成验证。
开发人员:
1)对比完整图和背景图的区别,得到阴影位置
2)计算需要滑动的距离:遍历完整图的每一个像素点,利用 getRGB 对比完整图和缺口图哪里有差异,在有差异的时候,返回横坐标,即需要滑动的距离
3)拖动滑块,看效果
参考链接
相关文章:

常见的验证码
一、短信验证码 前端: 用户填写手机号,点击按钮发送请求用户短信得到验证码后,用户填写表单提交 form 表单,进行验证 后台: 随机生成几位验证码并将生成时间、手机号、验证码存储起来,可以存到session、…...

11. C语言标准函数库
C语言制定了一组使用方式通用的函数,称为C语言标准函数库,用于实现编程常用功能,标准函数库由编译器系统提供,并按功能分类存储在不同源代码文件中,调用标准库内函数时需要首先使用 #include 连接对应的源代码文件。 【…...

2016年认证杯SPSSPRO杯数学建模C题(第一阶段)如何有效的抑制校园霸凌事件的发生解题全过程文档及程序
2016年认证杯SPSSPRO杯数学建模 C题 如何有效的抑制校园霸凌事件的发生 原题再现: 近年来,我国发生的多起校园霸凌事件在媒体的报道下引发了许多国人的关注。霸凌事件对学生身体和精神上的影响是极为严重而长远的,因此对于这些情况我们应该…...

设计模式-抽象工厂模式实践案例
抽象工厂模式(Abstract Factory Pattern)是一种创建型设计模式,它提供了一个接口,用于创建一系列相关或相互依赖的对象,而无需指定它们具体的类。抽象工厂模式是围绕一个超级工厂创建其他工厂的模式。该模式的实现涉及…...

用readproc函数读取进程的状态
概要: 本篇演示用readproc函数读取进程的状态 libprocps库的安装参考笔者的文章readproc.h-CSDN博客 演示所用的系统是Ubuntu22.04 一、代码 #include<stdio.h> #include<stdlib.h> #include<proc/readproc.h> int main() {struct PROCTAB *…...
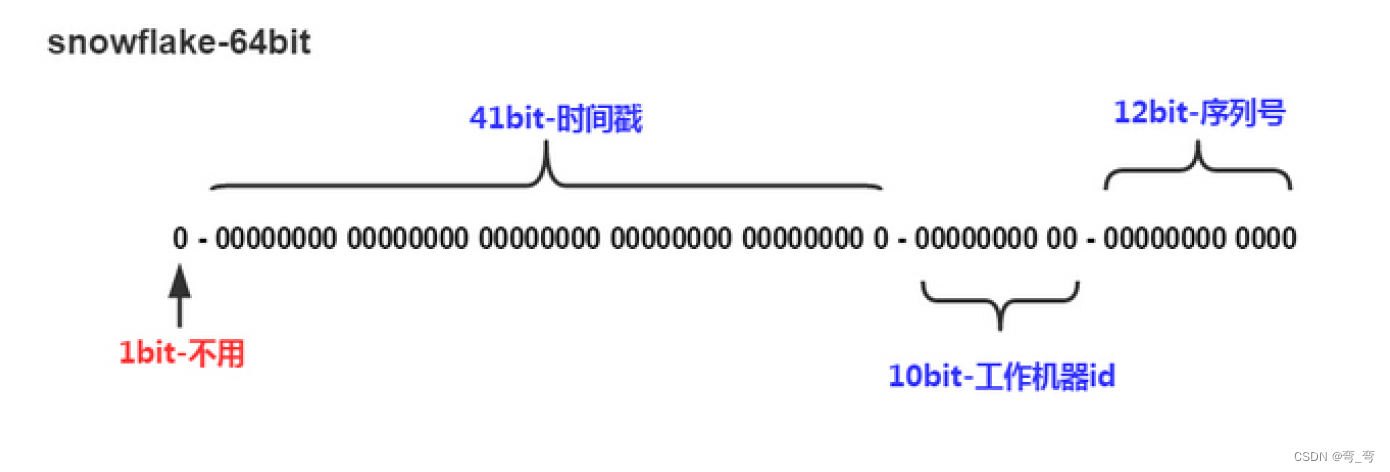
在高并发、高性能、高可用 三高项目中如何设计适合实际业务场景的分布式id(一)
分布式ID组件:黄金链路上的关键基石 在现代分布式系统中,分布式ID组件无疑扮演着至关重要的角色。作为整个系统的黄金链路上的关键组件,它的稳定性和可靠性直接关乎到整个系统的正常运作。一旦分布式ID组件出现问题,黄金链路上的…...
redis最新版本在Windows系统上的安装
一、说明 这次安装操作主要是根据redis官网说明,一步步安装下来的,英语比较好的同学,可以直接看文章底部的超链接1,跳到官网按步操作即可。 目前redis的最新稳定版本为redis7.2。 二、Windows环境改造 Redis在Windows上不被官方…...

【深度优先】【图论】【C++算法】2045. 到达目的地的第二短时间
作者推荐 视频算法专题 LeetCode2045. 到达目的地的第二短时间 城市用一个 双向连通 图表示,图中有 n 个节点,从 1 到 n 编号(包含 1 和 n)。图中的边用一个二维整数数组 edges 表示,其中每个 edges[i] [ui, vi] 表…...

思维题(蓝桥杯 填空题 C++)
目录 题目一: 编辑 代码: 题目二: 代码: 题目三: 代码: 题目四: 代码: 题目五: 代码: 题目六: 代码七: 题目八&#x…...

Meta的Llama2模型已上线!但我为何更推荐你从HuggingFace获取?还有Code Llama等你来解锁!
嘿,朋友们,今天给你们介绍一个新东西——Llama2模型,这是Meta(对,就是Facebook那家)推出的。 你可以直接去Llama的官网下载这个模型,然后按照他们GitHub上的指南来调用。 不过呢,我…...
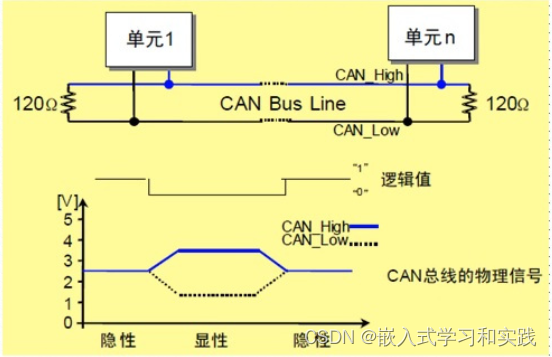
CAN总线及通讯的工作原理
一、CAN总线 CAN是控制器局域网络(Controller Area Network)的简称, 它是由研发和生产汽车电子产品著称的德国BOSCH公司开发的, 并最终成为国际标准(ISO11519),是国际上应用最广泛的现场总线之一。 二、工作原理 …...

linux下修改网卡MAC地址
我建议你使用 macchanger,但如果你不想使用它,那么可以使用另一种方法在 Linux 中更改 MAC 地址。 首先,使用以下命令关闭网卡: sudo ip link set dev enp0s31f6 down 接下来,使用以下命令设置新的 MAC:…...
47、WEB攻防——通用漏洞Java反序列化EXP生成数据提取组件安全
文章目录 序列化和反序列化的概念: 序列化:把java对象转换成字节流的过程;反序列化:把字节流恢复为java对象的过程。 对象的序列化主要有两种用途: 把对象的字节流永久的保存在硬盘上,通常存放在一个文件…...
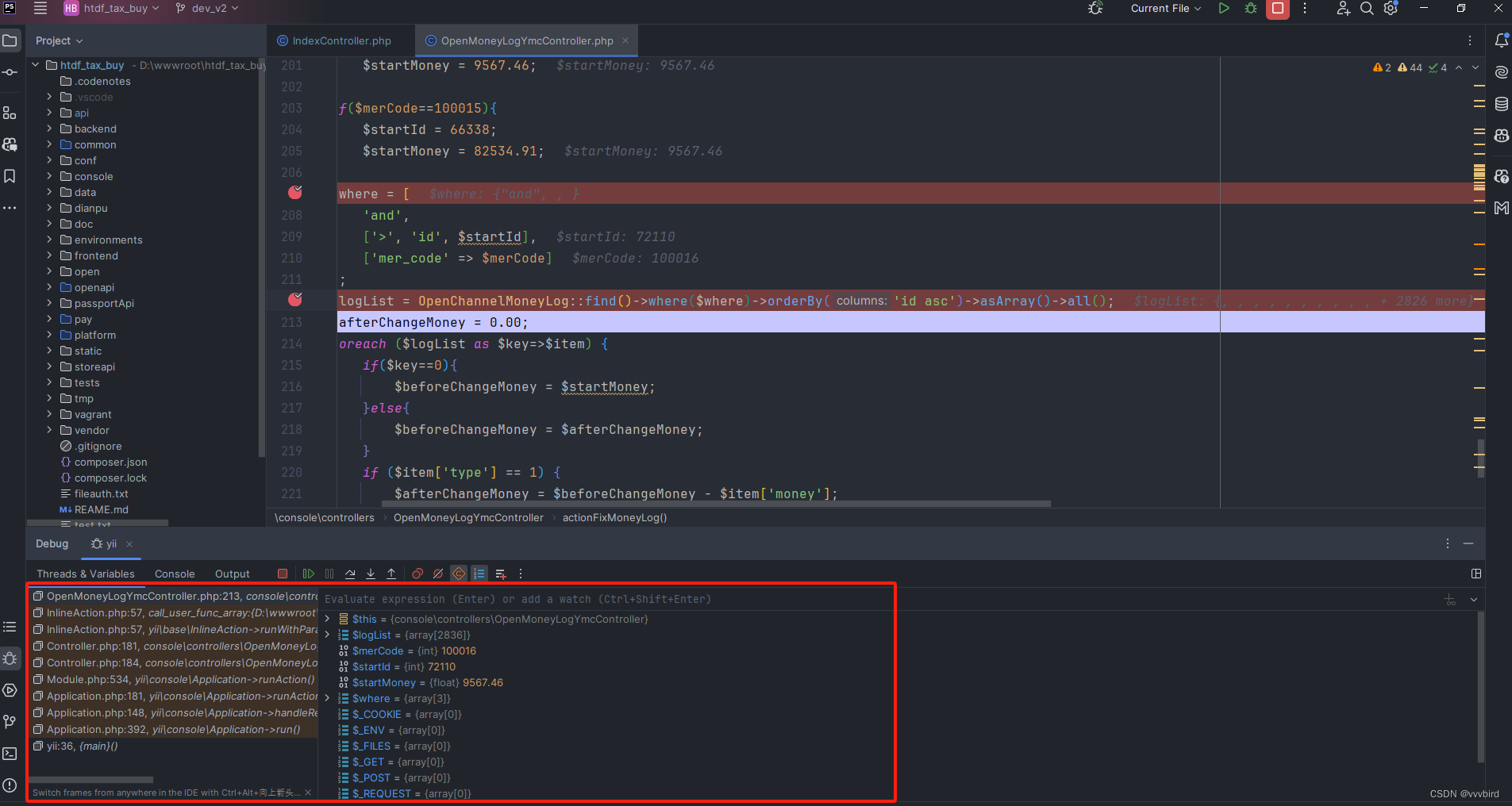
phpstorm console xdebug
1.所有配置跟浏览器http请求一样 2.记得Current File 必须是controller文件 注意:如果没有出发断点,则echo phpinfo(),查看remote_port 和phpstorm 配置是否对上。...

Vue template到render过程
Vue template到render过程 vue的模版编译过程主要如下:template -> ast -> render函数(1)调用parse方法将template转化为ast(抽象语法树)(2)对静态节点做优化(3)生…...

【你也能从零基础学会网站开发】Web建站之HTML+CSS入门篇 CSS常用属性
🚀 个人主页 极客小俊 ✍🏻 作者简介:web开发者、设计师、技术分享 🐋 希望大家多多支持, 我们一起学习和进步! 🏅 欢迎评论 ❤️点赞💬评论 📂收藏 📂加关注 CSS常用属性…...

Golang 写日志到文件
package mainimport ("log""os""time" )func main() {printLog("auto", "报警内容AA") }func printLog(filename string, content string) {t : time.Now().Format(time.DateOnly)file : filename "." t "…...
数字孪生10个技术栈:数据处理的六步骤,以获得可靠数据。
一、什么是数据处理 在数字孪生中,数据处理是指对采集到的实时或历史数据进行整理、清洗、分析和转化的过程。数据处理是数字孪生的基础,它将原始数据转化为有意义的信息,用于模型构建、仿真和决策支持。 数据处理是为了提高数据质量、整合数…...
之centos搭建jenkins)
运维随录实战(5)之centos搭建jenkins
一,搭建jenkins准备 下载安装jdk环境 -》版本 jdk11 下载安装maven环境 -》版本 maven 3.8.8 git -》版本 1.8.3.1 yum install git jenkins安装版本:2.414.3 下载地址:https://get.jenkins.io/war-stable/2.414.3/jenkins.war 注:jenkins版本与jdk版本有一定的对应关…...
css clip-path polygon属性实现直角梯形
2024.3.8今天我学习了如何用css实现直角梯形的效果, 效果: 具体实现原理: 一、需要三个div: 外面一个大的div,里面左右两个小的div 我们需要先把第一个div变成直角梯形: 大概是这样,设置好之…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

前端工具库lodash与lodash-es区别详解
lodash 和 lodash-es 是同一工具库的两个不同版本,核心功能完全一致,主要区别在于模块化格式和优化方式,适合不同的开发环境。以下是详细对比: 1. 模块化格式 lodash 使用 CommonJS 模块格式(require/module.exports&a…...
