LeetCode-数组-前缀和-中等难度
前缀和
前缀和是一种利用预处理的方式来减少整体实现复杂度的方法。
基本定理
假设原数列A为:[1,2,3,4,5],与之对应的前缀和数列P则为:[1,3,6,10,15]
前缀和数列的第一项等于原数列的第一项,从第二项开始前缀和数列每一项计算方法为:P[i] = P[i-1]+A[i]
原数列A与前缀和数列P则有以下几种关系:
- 前缀和数列从第二项起,每一项
(i)与它的前一项(i - 1)的差等于原数列(i)的值。 - 前缀和数列每一项
(i)等于原数列中(0 ~ i)项之和。 - 在满足
0 < i < j时,原数列的第(i ~ j)项之和等于前缀和数列的第(j)项减去第(i - 1)项。
根据这样的关系,在某些应用场景上我们就可以利用前缀和进行快速求解。
1. 区域和检索 - 数组不可变
题目描述

解题思路
根据前面定理中的第三条,可以发现利用前缀和可以快速实现这个需求。
代码实现
这里为了方便计算,额外忽视了前缀和数列的第一位,比如数列为:{1,2,3,4,5},对应的前缀和数列为:{0,1,3,6,10,15},其中第一位数值0,没有任何含义,只是为了方便处理。
class NumArray {private int[] preSum;public NumArray(int[] nums) {preSum = new int[nums.length + 1];for(int i = 0; i < nums.length; i++){preSum[i + 1] = preSum[i] + nums[i];}}public int sumRange(int left, int right) {// 本身根据定理应该是p[right] - p[left - 1],// 但由于我们将前缀和数列整体右移了一位,因此就变成了p[right + 1] - p[left],// 这样做的好处是,不用单独处理当left为0的情况了。return preSum[right + 1] - preSum[left];}
}
2. 除自身以外数组的乘积
题目描述

解题思路
本题可以考虑从后向前遍历,那么每一项之前的元素乘积,如果用前缀和思路来处理的话,就是前面定理中的第二条。(符合前缀和的也符合前缀乘积)
比如原数列:{1,2,3,4},前缀积数列:{1,2,6,24},则遍历原数列最后一位4时,对应的之前所有数的乘积就是前缀积数列的倒数第二位6。
现在已经搞定了除目标元素外的左边所有元素的乘积,只要再计算出其右边所有元素的乘积即可。
依据同样的思想,你也可以做一个后缀积来方便直接获取,但就当前这个场景来说倒也没必要,对于右边元素我们只需要直接动态维护即可。
代码实现
class Solution {public int[] productExceptSelf(int[] nums) {int n = nums.length;int[] preSum = new int[n + 1];// 前缀数列第一位无实际意思,仅仅为了方便处理preSum[0] = 1;for (int i = 1; i < n + 1; i++) {preSum[i] = preSum[i - 1] * nums[i - 1];}// 右边元素动态维护int rightSum = 1;int[] ans = new int[n];for (int i = n - 1; i >= 0; i--) {ans[i] = preSum[i] * rightSum;rightSum *= nums[i];}return ans;}
}
3. 和相同的二元子数组
题目描述

解题思路
假设有:原数列1 0 1 0 1 ,和与其对应的前缀和数列:1 1 2 2 3。
- 我们知道子数组可以看作
[left,right]这样一个区间,并且left和right满足:0 <= left <= right. - 所以本题可以看作是在要求
0 <= left <= right这样一个区间内的所有元素和等于goal。 - 我们看到求解
0 <= left <= right这样一个区间之和,就可以思考一下是否可以利用前缀和的性质。很明显在前缀和数列中只需要通过计算right - (left - 1),即可得到原数列的0 <= left <= right区间之和。 - 经过上面3步分析,最终就变成了求
right - (left - 1)等于goal的个数。
所以最终我们只需要构造一个前缀和数列,然后通过嵌套循环的方式,以每个right为子数组的结束区间,挨个检查子数组的开始区间即可。
public int numSubarraysWithSum(int[] nums, int goal) {int[] perSum = new int[nums.length + 1];for (int i = 0; i < nums.length; i++) {perSum[i + 1] = perSum[i] + nums[i];}int ans = 0;for (int right = 1; right < perSum.length; right++) {for (int left = right; left > 0; left--) {if (perSum[right] - perSum[left - 1] == goal) {ans++;}}}return ans;
}
复杂度优化
由于存在嵌套循环,因此复杂度较高,不难发现,每次内层循环中只是在计算在0~right-1下标对应的数值中有多少个等于perSum[right] - goal,因此我们考虑将每一个0~right-1对应的结果直接记录下来,这样不就可以省去内层循环的处理了吗~
public int numSubarraysWithSum(int[] nums, int goal) {int[] perSum = new int[nums.length + 1];for (int i = 0; i < nums.length; i++) {perSum[i + 1] = perSum[i] + nums[i];}int ans = 0;// key表示前缀和数列坐标对应的值,value表示改值出现的次数Map<Integer, Integer> map = new HashMap<>();// 前缀和第一位坐标0需特殊处理一下,对应的值为0,出现1次。map.put(0, 1);for (int right = 1; right < perSum.length; right++) {if (map.containsKey(perSum[right] - goal)) {ans += map.get(perSum[right] - goal);}map.put(perSum[right], map.getOrDefault(perSum[right], 0) + 1);}return ans;
}
如果还想简化一点,则可以动态维护前缀和数组,如下:
public int numSubarraysWithSum(int[] nums, int goal) {int ans = 0;Map<Integer, Integer> map = new HashMap<>();map.put(0, 1);int perSum = 0;for (int right = 0; right < nums.length; right++) {perSum += nums[right];if (map.containsKey(perSum - goal)) {ans += map.get(perSum - goal);}map.put(perSum, map.getOrDefault(perSum, 0) + 1);}return ans;
}
类似题型
与之类似的题目还有:
560.和为K的子数组
974.和可被 K 整除的子数组
4. 连续的子数组和
题目描述

解题思路
本题关键在于解决子数组元素总和为K的倍数这个问题。
首先,我们发现是求解子数组的问题,通过前面的练习,我们知道在前缀和数列中,求解子数组的和,等同于求解其前缀和数组的right - (left - 1)。
同余定理
给定一个正整数m,如果两个整数a和b满足a-b能够被m整除,即(a-b)/m得到一个整数,那么就称整数a与b对模m同余,记作a≡b(mod m)。
因此,如果(right - (left - 1))是K的整数倍,则根据同余定理则有 right % k == (left - 1) % k。
有了这个结论以后,接下来的处理方式就和前面差不多了,通过一个哈希表用Key记录每一项的余数,Value用来记录下标,为了满足题目中大小至少为2的要求,下标位置不更新。
代码实现
public boolean checkSubarraySum(int[] nums, int k) {int sum = 0;Map<Integer, Integer> map = new HashMap<>();map.put(0, -1);for (int i = 0; i < nums.length; i++) {sum += nums[i];int mod = sum % k;if (map.containsKey(mod)) {if (i - map.get(mod) >= 2) {return true;}} else {map.put(mod, i);}}return false;
}
5. 连续数组
题目描述

解题思路
如果把拥有相同数量的0和1理解为互相抵消,假设我们有一个计数器C,当遇到0就减1,遇到1就加1,因此当C等于0时,则0和1的数量一定相同,所以这个题目就又变成了子数组求和的问题了,那么看到子数组求和就想到用前缀和数列来解。
我们知道子数组可以看作[left,right],其所有元素之和,又等于其对应的前缀和数列right - (left - 1)的计算结果,这个在前面几题中也一直在用,又因为如果right == (left - 1),则right - (left - 1)==0,也就是我们要求的结果,子数组区间内所有元素之和为0。所以,最后我们要求的其实就是长度最长的right == (left - 1)。
代码实现
public int findMaxLength(int[] nums) {Map<Integer, Integer> map = new HashMap<>();// 表示0值,出现的下标位置map.put(0, -1);int sum = 0;int ans = 0;for (int i = 0; i < nums.length; i++) {sum += nums[i] == 0 ? -1 : 1;if (map.containsKey(sum)) {ans = Math.max(ans, i - map.get(sum));} else {map.put(sum, i);}}return ans;
}
类似题型
与之类似的题目还有:
字母与数字
6. 和为奇数的子数组数目
题目描述

解题思路
还是求子数组和的问题,要求为奇数,我们知道,两奇数或两偶数相加结果为偶数,只有一奇一偶相加结果才为奇数。
所以,根据right - (left - 1)等于原数组的子数组之和,可以得出以下结论:
-
当
right为偶数时,left - 1必须为奇数,子数组之和才为奇数。 -
当
right为奇数时,left - 1必须为偶数,子数组之和才为奇数。
代码实现
public int numOfSubarrays(int[] arr) {int ans = 0;int mod = 1000000007;int odd = 0;int even = 1;int sum = 0;for (int i = 0; i < arr.length; i++) {sum += arr[i];ans = (ans + (sum % 2 == 0 ? odd : even)) % mod;if(sum % 2 == 0){even++;}else{odd++;}}return ans;
}
7. 统计「优美子数组」
题目描述

解题思路
可以把奇数的个数当做前缀和数列来记录,比如对于[1,1,2,1,1]这样的数列,对应的奇数前缀和数列为[0,1,2,2,3,4],每一项表示的是奇数个数(注意:0个奇数也是有计算含义的)。
那么如果子数组恰好有K个奇数,则有right - (left - 1) = K,转换一下也就是right - K = left - 1,这就回到了我们习惯的哈希表处理方式,无需说明,直接看代码。
代码实现
public int numberOfSubarrays(int[] nums, int k) {int ans = 0;int oddCnt = 0;Map<Integer, Integer> map = new HashMap<>();// 初始化map表示:出现0个奇数的次数为1map.put(0, 1);for (int i = 0; i < nums.length; i++) {if (nums[i] % 2 != 0) {oddCnt++;}if (map.containsKey(oddCnt - k)) {ans += map.get(oddCnt - k);}map.put(oddCnt, map.getOrDefault(oddCnt, 0) + 1);}return ans;
}
相关文章:

LeetCode-数组-前缀和-中等难度
前缀和 前缀和是一种利用预处理的方式来减少整体实现复杂度的方法。 基本定理 假设原数列A为:[1,2,3,4,5],与之对应的前缀和数列P则为:[1,3,6,10,15] 前缀和数列的第一项等于原数列的第一项,从第二项开始前缀和数列每一项计算…...

【程序人生】探索2024年AI辅助研发趋势
目录标题 探索2024年AI辅助研发趋势一、AI在编码中的应用智能代码生成助力开发错误检测与修复的即时反馈性能优化的智能建议 二、AI驱动的自动化工具三、AI与团队协作四、未来展望结语 探索2024年AI辅助研发趋势 随着人工智能技术的迅速发展,AI在各个领域的应用正日…...
集合框架(一)Collection
学习过了ArrayList,知道集合是一种容器,用来装数据的,类似于数组,但集合的大小可变,开发中也非常常用。 为了满足不同的业务场景需求Java还提供了很多不同特点的集合给我们选择。 集合体系结构 Collection是一个接口&a…...
Android 性能优化--APK加固(2)加密
文章目录 字符串加密图片加密如何避免应用被重新签名分发APK 加壳的方案简析DEX加密原理及实现 本文首发地址:https://h89.cn/archives/212.html 最新更新地址:https://gitee.com/chenjim/chenjimblog 通过 前文 介绍,我们知晓了如何使用代码…...
Linux环境下使用interrupt方式操作UART
目录 概述 1 Linux环境下UART设备 2 轮询方式操作UART功能实现 2.1 打开串口函数:usr_serial_open 2.2 关闭串口函数: usr_serial_close 2.3 发送数据函数: usr_serial_sendbytes 2.4 接收数据函数: usr_serial_readinterr…...
修改Android打包apk的名字和目录
app打包生成apk后通常需要进行备份,但是要区分好哪个apk是什么版本的、什么时候打包的,以方便以后区分使用。 最开始的想法是把版本号、创建时间这些加在apk文件名上即可,但是公司要求apk使用一个固定的名称,那我怎么保存版本号信…...
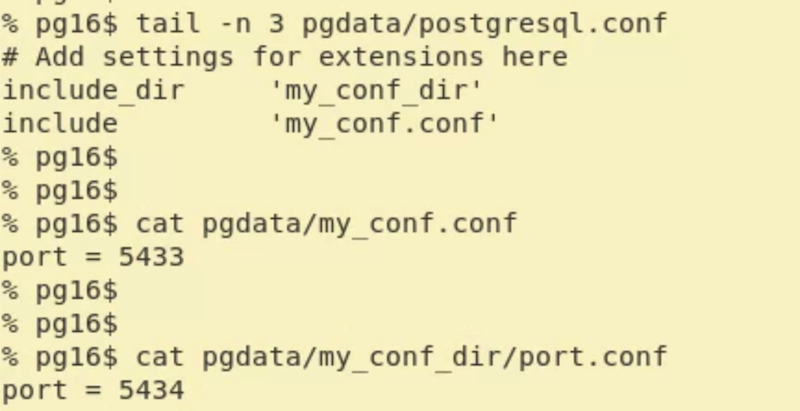
管理 PostgreSQL 中配置参数的各种方法
管理 PostgreSQL 中配置参数的各种方法 1. 概述 PostgreSQL提供了一个配置文件 postgresql.conf 让用户自定义参数。您可能需要更改一些参数来调整性能或在工作环境中部署 PostgreSQL 服务器。在这篇博文中,我们将探索管理这些参数的不同方法。 2. 以不同方式管理…...
)
Linux命令-continue命令(结束本次循环,继续执行下一个for,while或until循环。)
概要 continue [n]主要用途 结束本次循环,继续执行下一个for,while或until循环;可指定从第几层循环继续执行。 参数 n(可选):大于等于1的整数,用于指定从第几层循环继续执行。 返回值 返回…...
智能部署之巅:Amazon SageMaker 引领机器学习革新
本篇文章授权活动官方亚马逊云科技文章转发、改写权,包括不限于在 亚马逊云科技开发者社区, 知乎,自媒体平台,第三方开发者媒体等亚马逊云科技官方渠道。 (全球 TMT 2023年12月6日讯)亚马逊云科技在 2023 re:Invent 全…...

国内哪个工具可以平替chatgpt?国内有哪些比较好用的大模型gpt?
我自己试用了很多的平台,发现三个比较好的大模型平台,对普通用户也比较的友好的,而且返回内容相对来说,正确率更高的,并且相关场景插件比较丰富的国内厂商。 本文说的,是我自己觉得的,比较有主观…...

python如何打包py文件为exe
要将Python程序打包为可执行文件(.exe),您可以使用一些第三方工具。以下是两个常用的工具:PyInstaller和cx_Freeze。 使用PyInstaller PyInstaller是一个流行的Python打包工具,可以将Python程序及其所有依赖项打包为…...

yolov9网络结构图
文章目录 配置文件主干分支backbone预测头headyolov9网络结构图 系列文章目录 论文链接:👿 YOLOv9: Learning What You Want to Learn Using Programmable Gradient Information代码链接:👿 https://github.com/WongKinYiu/yolov9…...
Spark 核心API
核心 API spark core API 指的是 spark 预定义好的算子。无论是 spark streaming 或者 Spark SQL 都是基于这些最基础的 API 构建起来的。理解这些核心 API 也是写出高效 Spark 代码的基础。 Transformation 转化类的算子是最多的,学会使用这些算子就应付多数的数…...

OpenLayers线性渐变和中心渐变(径向渐变)
目录 1.前言2.添加一个面要素3.线性渐变3.1 第一个注意点3.2 第二个注意点 4.中心渐变(径向渐变)5.总结 1.前言 OpenLayers官网有整个图层的渐变示例,但是没有单个要素的渐变示例,我们这里来补充一下。OpenLayers中的渐变是通过fi…...
)
[210. 课程表 II] 拓扑排序模板(DFS+BFS)
Problem: 210. 课程表 II 文章目录 思路解题方法Code 思路 本题是经典拓扑排序模板,通过DFS和BFS两种方式进行实现。 解题方法 DFS DFS方法的重点在于如何标记节点状态,初做题者如果只用未访问和已访问两种状态很容易陷入死结。正确的做法是使用三种状…...

我的第一个python web 网站
# -*- coding: utf-8 -*-import http.server import socketserver from datetime import datetimePORT 8000import sys# ...class MyHandler(http.server.SimpleHTTPRequestHandler):def do_GET(self):if self.path /:# 如果路径是根路径,返回页面内容self.send_r…...
产品展示型wordpress外贸网站模板
孕婴产品wordpress外贸网站模板 吸奶器、待产包、孕妇枕头、护理垫、纸尿裤、孕妇装、孕婴产品wordpress外贸网站模板。 https://www.jianzhanpress.com/?p4112 床品毛巾wordpress独立站模板 床单、被套、毛巾、抱枕、靠垫、围巾、布艺、枕头、乳胶枕、四件套、浴巾wordpre…...
四信全球化拓展再启新篇!LoRa传感器与云平台领航智能感知时代
随着科技浪潮的不断推进,物联网已逐渐融入我们的生活。刚刚结束的MWC24盛会上,四信带来了一系列前沿技术成果,不仅将5G技术成功扩展至当前市场主流类型的终端,更携手联通、ASR等业界巨头,在连接、5G RedCap、AI、LoRa以…...
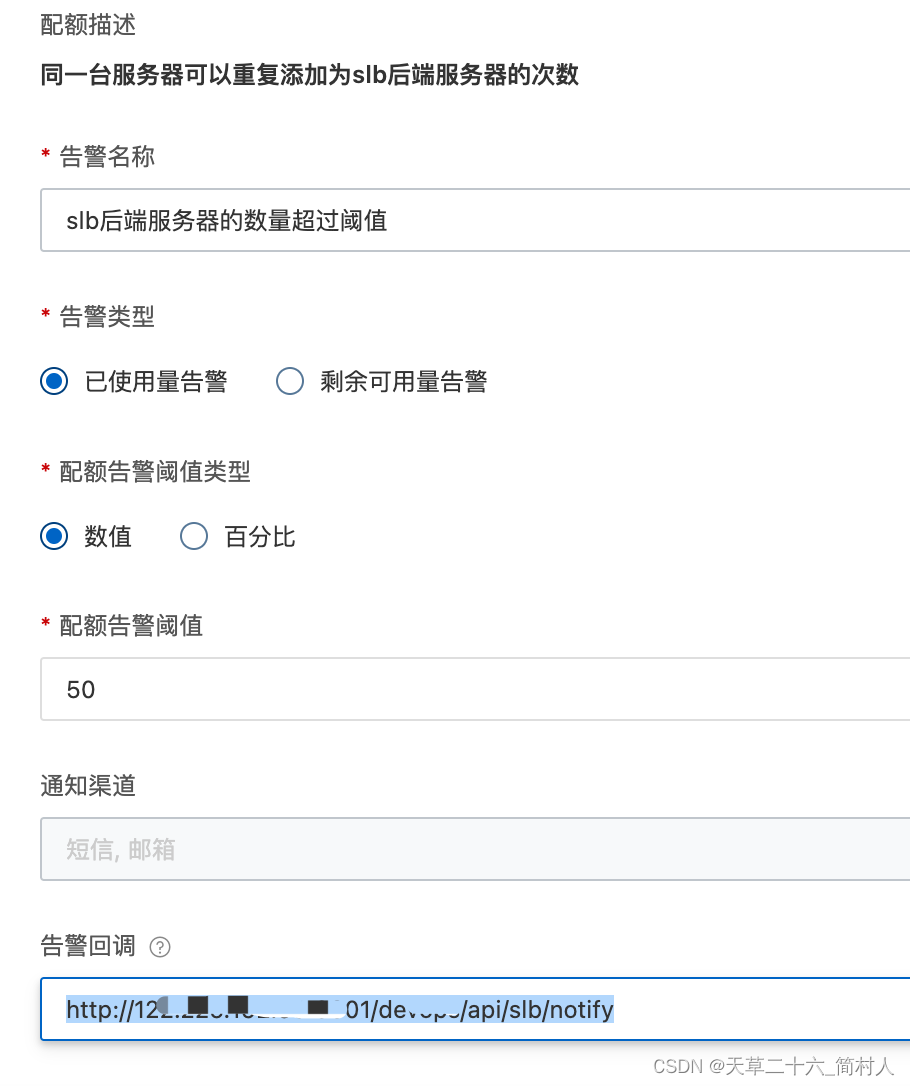
阿里云k8s环境下,因slb限额导致的发布事故
一、背景 阿里云k8s容器,在发布java应用程序的时候,客户端访问出现500错误。 后端服务是健康且可用的,网关层大量500错误请求,slb没有流入和流出流量。 经过回滚,仍未能解决错误。可谓是一次血的教训,特…...

【STM32+OPENMV】矩形识别
一、准备工作 有关OPENMV最大色块追踪及与STM32通信内容,详情见【STM32HAL】与OpenMV通信 二、所用工具 1、芯片:STM32F103C8T6 2、CUBEMX配置软件 3、KEIL5 4、OPENMV 三、实现功能 寻找黑色矩形,并将最大矩形的四个边缘坐标发送给STM…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...

13.10 LangGraph多轮对话系统实战:Ollama私有部署+情感识别优化全解析
LangGraph多轮对话系统实战:Ollama私有部署+情感识别优化全解析 LanguageMentor 对话式训练系统架构与实现 关键词:多轮对话系统设计、场景化提示工程、情感识别优化、LangGraph 状态管理、Ollama 私有化部署 1. 对话训练系统技术架构 采用四层架构实现高扩展性的对话训练…...

【多线程初阶】单例模式 指令重排序问题
文章目录 1.单例模式1)饿汉模式2)懒汉模式①.单线程版本②.多线程版本 2.分析单例模式里的线程安全问题1)饿汉模式2)懒汉模式懒汉模式是如何出现线程安全问题的 3.解决问题进一步优化加锁导致的执行效率优化预防内存可见性问题 4.解决指令重排序问题 1.单例模式 单例模式确保某…...
——Oracle for Linux物理DG环境搭建(2))
Oracle实用参考(13)——Oracle for Linux物理DG环境搭建(2)
13.2. Oracle for Linux物理DG环境搭建 Oracle 数据库的DataGuard技术方案,业界也称为DG,其在数据库高可用、容灾及负载分离等方面,都有着非常广泛的应用,对此,前面相关章节已做过较为详尽的讲解,此处不再赘述。 需要说明的是, DG方案又分为物理DG和逻辑DG,两者的搭建…...

Linux 内核内存管理子系统全面解析与体系构建
一、前言: 为什么内存管理是核心知识 内存管理是 Linux 内核最核心也最复杂的子系统之一,其作用包括: 为软件提供独立的虚拟内存空间,实现安全隔离分配/回收物理内存资源,维持系统稳定支持不同类型的内存分配器,最优…...
