树状数组+离散化求逆序对超详细讲解!
树状数组+离散化求逆序对
用一个数组 w [ ] w[] w[]来记录遍历到当前数时,每个数出现的次数
由于只关心每个数前边有多少个数比他大,遍历到 i i i时,求大于 a [ i ] a[i] a[i]的数有多少个,就是对 [ a [ i ] , n ] [a[i], n] [a[i],n]求和。
之后将 a [ i ] a[i] a[i]的出现次数 w [ a [ i ] ] + 1 w[a[i]]+1 w[a[i]]+1再求后边的答案。
如果暴力来做是 O ( n 2 ) O(n^2) O(n2)的(不知道这个对不对,不过不重要)
for (int i = 1; i <= n; i++) {int cnt = 0;for (int j = a[i]; j <= n; j++) {cnt += w[j];}ans += cnt;w[a[i]]++;
}
发现即要做单点修改 w [ a [ i ] ] + 1 w[a[i]] + 1 w[a[i]]+1,又要做区间查询 ∑ j = a [ i ] n w [ j ] \sum\limits_{j=a[i]}^{n} w[j] j=a[i]∑nw[j],于是用树状数组维护 w [ ] w[] w[]来降低复杂度。
回顾树状数组的两个操作:区间查询 + 单点修改
q u e r y ( i ) 表示查询区间 [ 1 , i ] 的和 query(i)表示查询区间[1, i]的和 query(i)表示查询区间[1,i]的和
a d d ( i , k ) 表示将含有 a [ i ] 的点都 + k add(i, k)表示将含有a[i]的点都+k add(i,k)表示将含有a[i]的点都+k
(实际上这里说的树状数组是权值树状数组,就是记录每个数出现的次数的树状数组)
一个前提:只关心相对大小,数本身有多大我并不关心,所以可以离散化(否则数据太大的话 w [ ] w[] w[]放不下那么大的下标会爆掉)
写法1
按照每个数的大小降序排序,如果大小相等则按照位置降序排序(考虑为什么这么做?)
假设在排序后的数组中第 i i i个数的原位置为 p [ i ] p[i] p[i],树状数组维护的是,每个原位置的数是否出现。
比如:
原数组:3 2 1 5 4
下标 :1 2 3 4 5排序后:5 4 3 2 1
原位置:4 5 1 2 3遍历到第2个数4时,记录情况为:[0, 0, 0, 1, 0],即原位置为4的数已经出现了。
我们知道4的原位置为5,此时对区间[1, 5]求和,就是原位置5对应的逆序对数量。
把原位置5记录进去。遍历到第3个数3时,记录情况为:[0, 0, 0, 1, 1],原位置4 5的数已经出现了
知道3的原位置为1,此时对区间[1, 1]求和,就是原位置1对应逆序对的数量。
把原位置1记录进去。遍历到第4个数2时,记录情况为:[1, 0, 0, 1, 1],原位置1 4 5的数已经出现了
知道2的原位置为2,此时对区间[1, 2]求和,就是原位置2对应逆序对的数量。
把原位置2记录进去。遍历到第5个数1时,记录情况为:[1, 1, 0, 1, 1],原位置1 2 4 5的数已经出现了
知道1的原位置为3,此时对区间[1, 3]求和,就是原位置3对应逆序对的数量。
把原位置3记录进去。
看懂这一丁点就行,下边是一顿胡扯,可以不看了
注意:以下所有情况都在排好序的数组中进行!!!
现在来考虑两个情况
1. 当前数是唯一的,不考虑相同数位置降序排序的情况
记第 i 个数为 a [ i ] , 排序前位置为 p [ i ] 记第i个数为a[i], 排序前位置为p[i] 记第i个数为a[i],排序前位置为p[i]
要查询这个位置对应的逆序对数量
因为我们已经按照降序进行了排序,就变为查询 位置在 p [ i ] p[i] p[i]之前且大于 a [ i ] a[i] a[i]的数的个数
对应到排序后的数组中就是:
前 i − 1 i - 1 i−1个数中原位置在 p [ i ] p[i] p[i]之前的数。
因为排序已经确保了前 i − 1 i - 1 i−1个数都是比 a [ i ] a[i] a[i]大的数,现在只需要在前 i − 1 i - 1 i−1个数中找到位置在 p [ i ] p[i] p[i]前的数就可以了
比他大的数在排序前只有两种情况:在他前边/在他后边
只有 (排序前在他前边) 的数才会构成逆序对,在他后边的数不会构成逆序对
再次强调,因为是降序排序,故已经确保了 (遍历到第 i i i个数时已经记录出现的数) 都是大于 a [ i ] a[i] a[i]的。
那么对于第 i i i个数,(比 a [ i ] a[i] a[i]大) 且 (在 p [ i ] p[i] p[i]之前出现) 的数的个数,实际上就是已经记录出现了的数的个数,即 [ 1 , p [ i ] ] [1, p[i]] [1,p[i]]的和。求区间 [ 1 , p [ i ] ] [1, p[i]] [1,p[i]]的和,就是 q u e r y ( p [ i ] ) query(p[i]) query(p[i])。
最后将这个位置的数记为出现, a d d ( p [ i ] , 1 ) add(p[i], 1) add(p[i],1)
2. 如果数不唯一
数不唯一的话按照位置降序排序
考虑一下,假设已经按照位置进行了降序排序
当前数为 a [ i ] a[i] a[i],位置 p [ i ] p[i] p[i]
排序后数组中在当前数之前的相同数 a [ j ] a[j] a[j],对应位置 p [ j ] p[j] p[j]一定在 p [ i ] p[i] p[i]后边
那么 [ 1 , p [ i ] ] [1, p[i]] [1,p[i]]求和时,是这样的一个区间:
1 2 3 4 ... p[i] ... p[j] ...
就不会把相同的数也算到逆序对中,这样就避免了重复计算。
总结一下核心:降序排序后每个位置 i i i要查询的区间和 [ 1 , p [ i ] ] [1,p[i]] [1,p[i]],是出现在原数组位置 p [ i ] p[i] p[i]之前且大于当前数的元素个数
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>#define debug(x) std::cerr << "#x" << " = " << x << ' '
#define DEBUG(x) std::cerr << "#x" << " = " << x << std::endltypedef long long ll;
using namespace std;const int N_MAX = 500000 + 10;int n;
int tr[N_MAX];
struct Node {int v, p;bool operator < (const Node& other) const {if (v != other.v) return v > other.v;return p > other.p;}
}a[N_MAX];int lowbit(int x) {return x & -x;
}void inc(int x, int v) {for (int i = x; i <= n; i += lowbit(i)) tr[i] += v;
}ll calc(int x) {ll sum = 0ll;for (int i = x; i >= 1; i -= lowbit(i)) sum += tr[i];return sum;
}int main() {cin >> n;for (int i = 1; i <= n; i++) cin >> a[i].v, a[i].p = i;sort(a + 1, a + n + 1);ll ans = 0ll;for (int i = 1; i <= n; i++) {ans += calc(a[i].p);inc(a[i].p, 1);}printf("%lld\n", ans);return 0;
}
相关文章:

树状数组+离散化求逆序对超详细讲解!
树状数组离散化求逆序对 用一个数组 w [ ] w[] w[]来记录遍历到当前数时,每个数出现的次数 由于只关心每个数前边有多少个数比他大,遍历到 i i i时,求大于 a [ i ] a[i] a[i]的数有多少个,就是对 [ a [ i ] , n ] [a[i], n] [a[i…...
《解密云计算:企业之选》
前言 在当今数字化时代,企业面临着巨大的数据处理压力和信息化需求,传统的IT架构已经无法满足日益增长的业务需求。在这样的背景下,越来越多的企业开始转向云计算,以实现灵活、高效和可扩展的IT资源管理和利用。 云计算 云计算是…...

地址分词 | EXCEL批量进行地址分词,标准化为十一级地址
一 需求 物流需要对用户输入地址进行检查,受用户录入习惯地址可能存在多种问题。 地址标准化是基于地址引擎和地址大数据模型,自动将地址信息标准化为省、市、区市县、街镇、小区、楼栋、单元、楼层、房屋、房间等元素,补充层级缺失数据、构建…...

KubeSphere平台安装系列之二【Linux单节点部署KubeSphere】(2/3)
**《KubeSphere平台安装系列》** 【Kubernetes上安装KubeSphere(亲测–实操完整版)】(1/3) 【Linux单节点部署KubeSphere】(2/3) 【Linux多节点部署KubeSphere】(3/3) **《KubeS…...
网络安全: Kali Linux 使用 docker-compose 部署 openvas
目录 一、实验 1.环境 2.Kali Linux 安装docker与docker-compose 3.Kali Linux 使用docker-compose方式部署 openvas 4. KaliLinux 使用openvas 二、问题 1. 信息安全漏洞库 2.信息安全漏洞共享平台 3.Windows 更新指南与查询 4.CVE 查询 5.docker-compose 如何修改o…...

【学习考试心得】在誉天学习考试RHCE9.0的体验
作为华中第一位参加RHCE9.0线上考试的考生,很荣幸能来写这个心得,和大家分享一下线上的考试的一些体验。 一、学习体验 首先在红帽课程的学习中,跟着杨峰老师的脚步,整个学习过程中都非常有意思。杨峰老师充满磁性的声音和小王老师…...

Flip Clock(not good)
最近体验了一下iOS的翻页时钟app,很想自己做一个,但是效果不好 public class main {public static void main(String[] args) {//psvmnew MyFrame();} }import javax.swing.*; import java.awt.*; import java.io.File; import java.io.IOException; im…...

目标检测——摩托车头盔检测数据集
一、简介 首先,摩托车作为一种交通工具,具有高速、开放和稳定性差的特点,其事故发生率高,伤亡率排在机动车辆损伤的首位。因此,摩托车乘员头盔对于保护驾乘人员头部安全至关重要。在驾乘突发状况、人体受冲击时&#…...
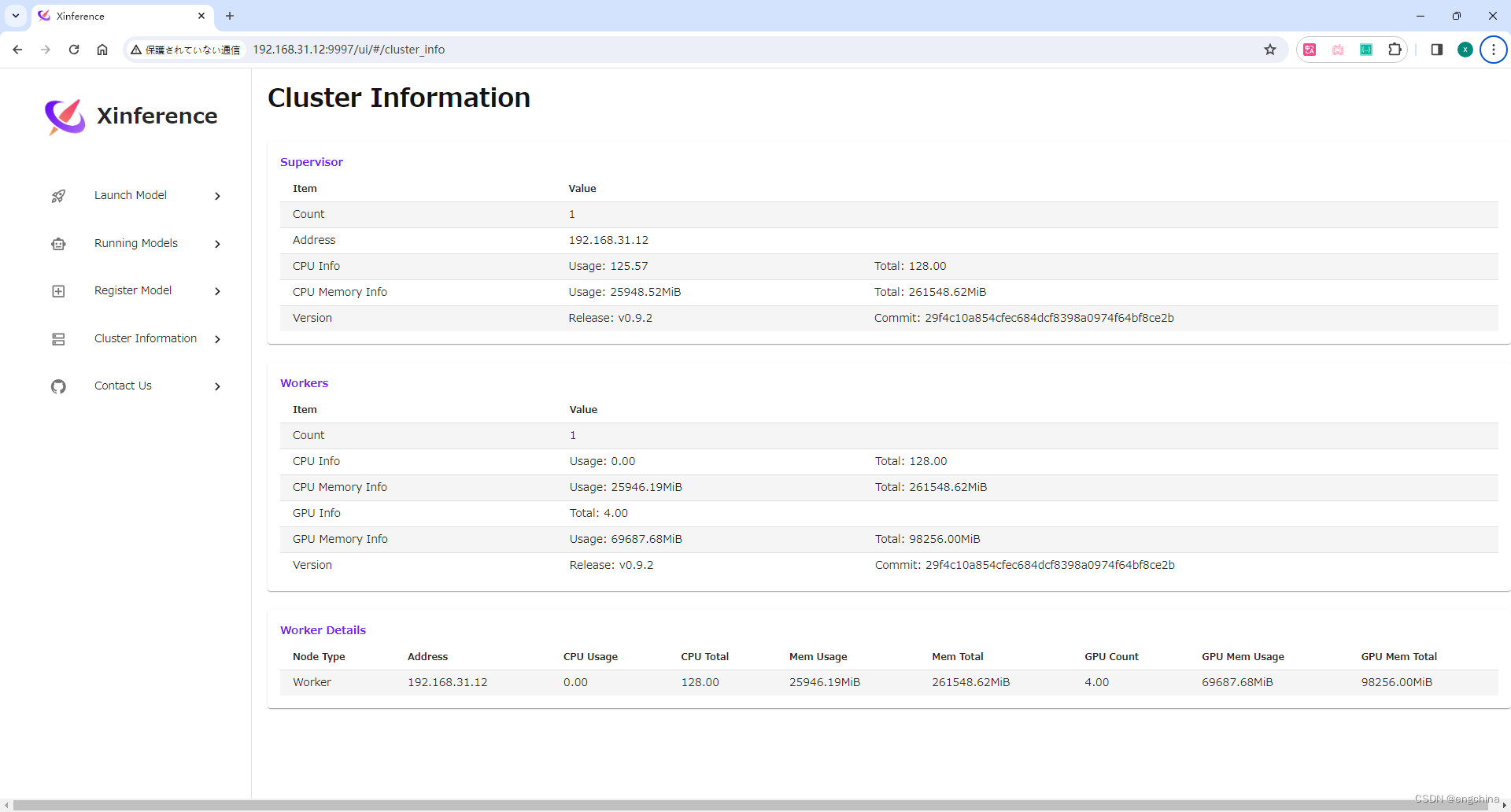
Windows 安装 Xinference
Windows 安装 Xinference 0. 引言1. 创建虚拟环境2. 安装 pytorch3. 安装 llama_cpp_python4. 安装 chatglm-cpp5. 安装 Xinference6. 设置 model 路径7. 启动 Xinference8. 查看 Cluster Information 0. 引言 Xorbits Inference(Xinference)是一个性能…...
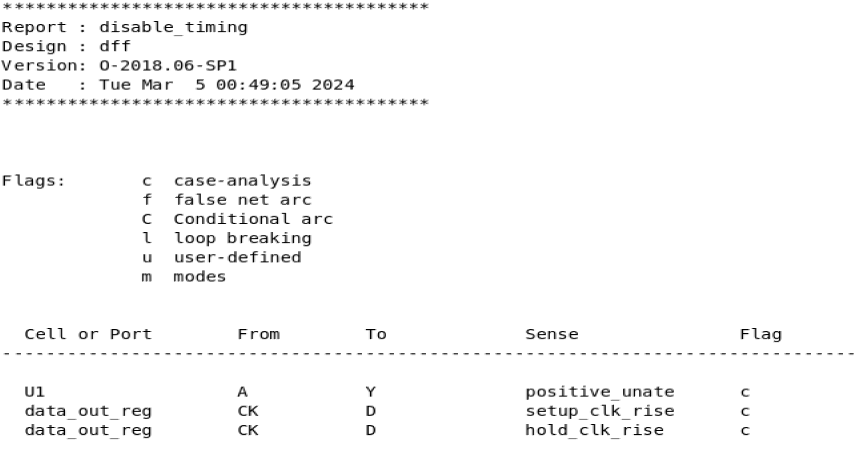
静态时序分析:SDC约束命令set_case_analysis详解
相关阅读 静态时序分析https://blog.csdn.net/weixin_45791458/category_12567571.html?spm1001.2014.3001.5482 目录 指定值 指定端口/引脚列表 简单使用 set_case_analysis命令用于对电路进行特定模式的设定,例如对于一个工作在正常模式下的芯片,…...
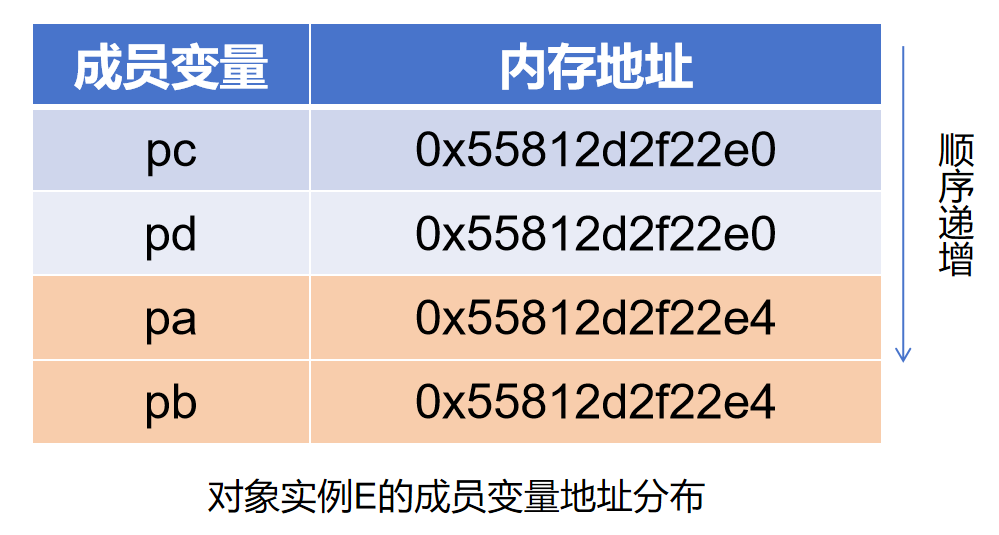
C++ · 代码笔记4 ·继承与派生
目录 前言010继承与派生简单例程020多级继承030使用using关键词更改访问权限040隐藏050派生类与基类成员函数同名时不构成重载060使用多级继承展示成员变量在内存中的分布情况071派生类在函数头调用基类构造函数072构造函数调用顺序080构造函数与析构函数的调用顺序091多重继承…...
解决uni-app中使用webview键盘弹起遮挡input输入框问题
这个平平无奇的回答,可能是全网最靠谱的解决方案。 这里我用的是vue3 setup .vue文件的方式 <view> <web-view :fullscreen"false" :webview-styles"{top: statusBarHeight40,height:height,progress: {color: green,height:1px } }"…...
Java注解介绍
Java注解 注解介绍元注解RetentionTargetDocumentedInherited接口类测试结果 注解介绍 Java注解(Annotation)是一种元数据(Metadata)的形式,它可以被添加到Java代码中的类、方法、变量、参数等元素上,以提…...
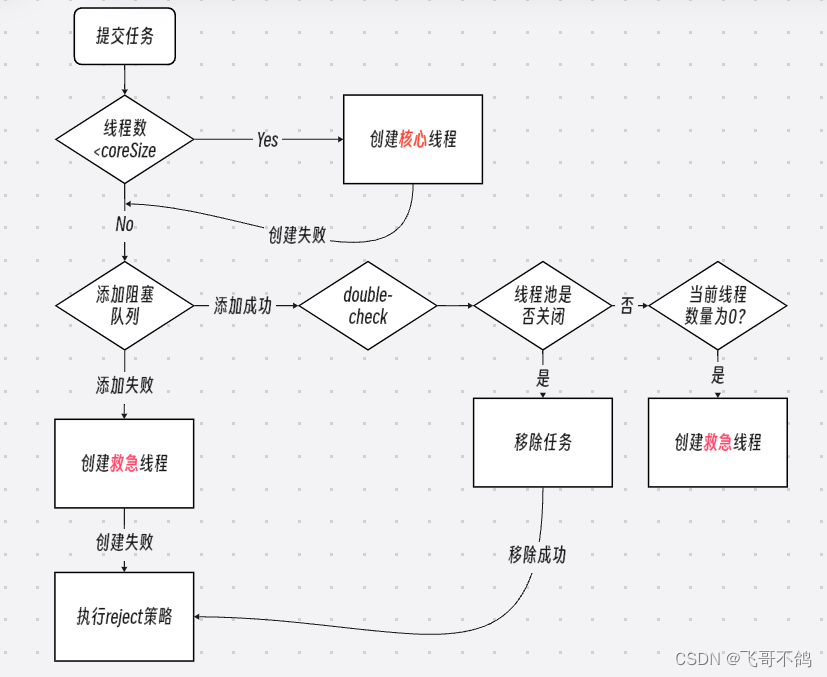
万字详解,Java实现低配版线程池
文章目录 1.什么是线程池2.线程池的优势3.原理4.代码编写4.1 阻塞队列4.2 ThreadPool线程池4.3 Worker工作线程4.4 代码测试 5. 拒绝策略5.1 抽象Reject接口5.2 BlockingQueue新增tryPut方法5.3 修改ThreadPool的execute方法5.4 ThreadPool线程池构造函数修改5.5 拒绝策略实现1…...

挂耳式蓝牙耳机哪家的好用?购买耳机前必须了解的几大要点
随着健康意识的提升,越来越多的人开始热衷于运动。运动不仅能够增强体质,对于我们这些忙碌的上班族而言,它也是一种极佳的减压方式。经过一天的辛勤工作,能够在户外跑步,让汗水带走压力,实在是一种享受。在…...

CSS文本属性
CSS文本属性 1.文本颜色2.文本间距3. 文本修饰4 .文本缩进5.文本对齐_水平6.行高7. vertical-align 1.文本颜色 属性名:color作用:控制文字的颜色。可选值: 颜色名rgb或rgbaHEX或HEXA (十六进制)HSL或HSLA 开发中常用…...

MySQL篇—执行计划之覆盖索引Using index和条件过滤Using where介绍(第三篇,总共三篇)
☘️博主介绍☘️: ✨又是一天没白过,我是奈斯,DBA一名✨ ✌✌️擅长Oracle、MySQL、SQLserver、Linux,也在积极的扩展IT方向的其他知识面✌✌️ ❣️❣️❣️大佬们都喜欢静静的看文章,并且也会默默的点赞收藏加关注❣…...

最短路径(2.19)
目录 1.网络延迟时间 弗洛伊德算法 迪杰斯特拉算法 2. K 站中转内最便宜的航班 3.从第一个节点出发到最后一个节点的受限路径数 4.到达目的地的方案数 1.网络延迟时间 有 n 个网络节点,标记为 1 到 n。 给你一个列表 times,表示信号经过 有向 边的…...
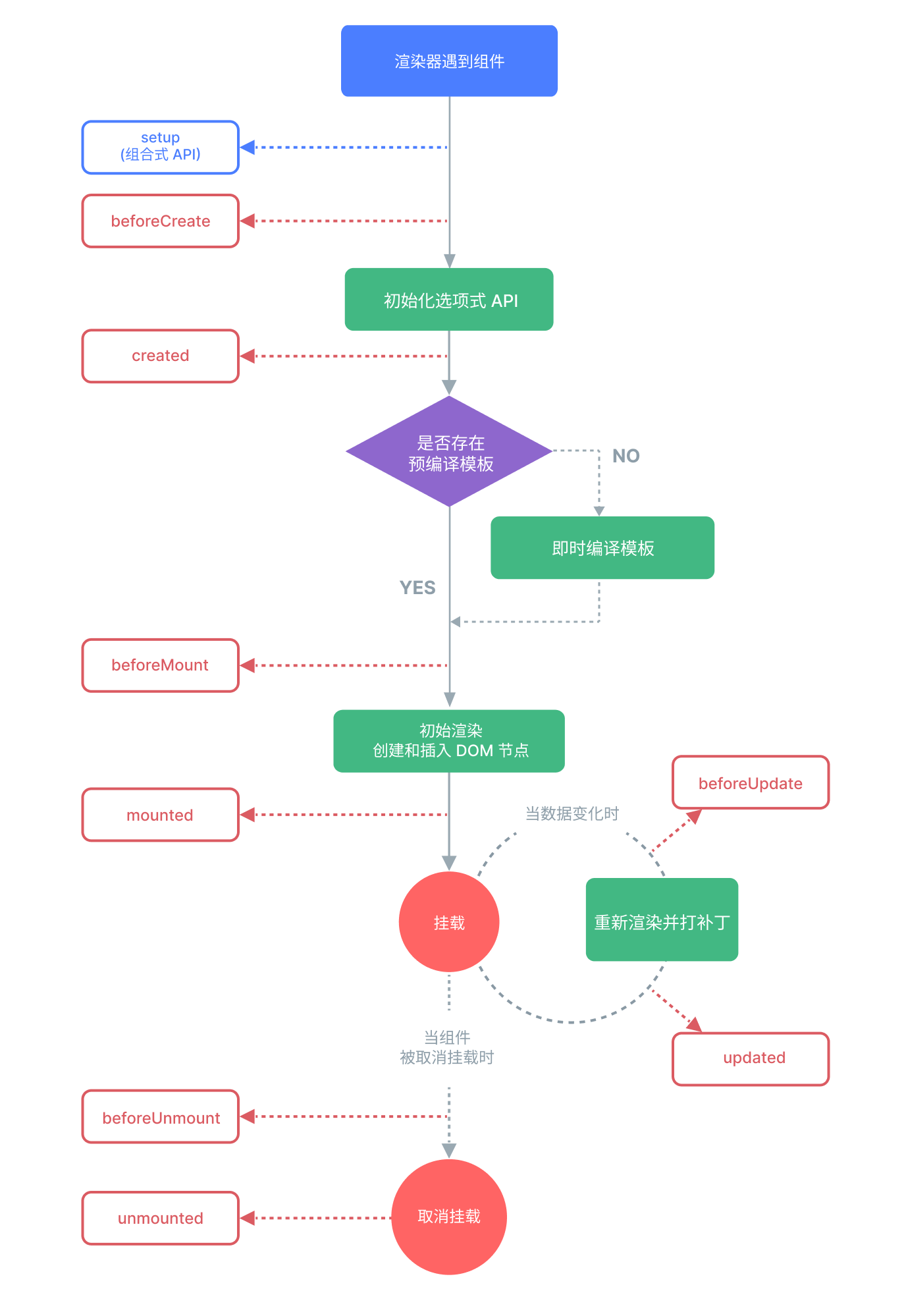
vue 总结
1.vue 的生命周期 1. es6 2. vue 基本属性指令 <template><div><!--<h1>vue基本指令的使用方式</h1><a :href"url">v-bind使用链接</a><img :src"srcUrl" /><div>解决闪烁问题<p v-cloak>{{…...

深入理解TCP/IP协议:互联网通信的核心
深入理解TCP/IP协议:互联网通信的核心 在数字化时代,TCP/IP协议是支撑全球互联网通信的基石。它不仅负责数据的传输和路由,还确保了信息传递的准确性和完整性。本文将深入探讨TCP/IP协议的工作原理、结构以及它在网络编程中的应用。 TCP/IP…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...
