AVL树讲解
AVL树
- 1. 概念
- 2. AVL节点的定义
- 3. AVL树插入
- 3.1 旋转
- 4.AVL树的验证
1. 概念
- AVL树是一种自平衡二叉搜索树。它的每个节点的左子树和右子树的高度差(平衡因子,我们这里按右子树高度减左子树高度)的绝对值不超过1。
- AVL的左子树和右子树都是AVL树。
- 比起二叉搜索树AVL树可以很好的优化二叉搜索树最坏的情况,使查询的效率达到O(log2 N)。
2. AVL节点的定义
和搜索二叉树节点相比,AVL树节点多了一个父节点和平衡因子(不是必要)需要维护。
template<class T>
typedef struct AVLTreeNode
{AVLTreeNode(const T& data):_pLeft(nullptr),_pRight(nullptr),_pParent(nullptr),_data(data),_bf(0){};//左节点、右节点、父节点AVLTreeNode<T>* _pLeft;AVLTreeNode<T>* _pRight;AVLTreeNode<T>* _pParent;T _data;//平衡因子int bf;
};
3. AVL树插入
和搜索二叉树的插入操作相比较,AVL树的插入需要多维护父节点和平衡因子。维护父节点比较简单,我们需要学习的是维护平衡因子。
当我们按照搜索二叉树的逻辑插入一个节点后,在插入这个节点之前父节点的平衡因子可能是-1/0/1这三种,如果该节点插入到父节点的左边需要将平衡因子减1,插入到右边则加1。所以插入之后平衡因子有这几种情况±1/0/±2。如果是±1,那么需要继续判断上面节点的平衡因子、如果是0,那么不需要判断了、如果是±2,那么就需要进行旋转操作。
3.1 旋转
我们先说结论:1、旋转之后节点所在子树的高度会回到插入之前。2、旋转不会对上面节点平衡因子产生影响。
- 右单旋
初始情况:
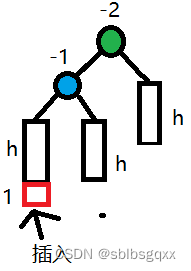
// 右单旋void RotateR(Node* pParent){Node* parent = pParent->_parent;//变成局部的根Node* pParentL = pParent->_left;Node* pParentR = pParentL->_right;if (pParent == _proot)_proot = pParentL;pParent->_left = pParentR;if (pParentR)pParentR->_parent = pParent;pParentL->_left = pParent;pParent->_parent = pParentL;pParentL->_parent = parent;//只需要修改pParent和pParentL的平衡因子pParent->_bf = 0;pParentL->_bf = 0;return;}
旋转之后情况

- 左单旋
初始情况:
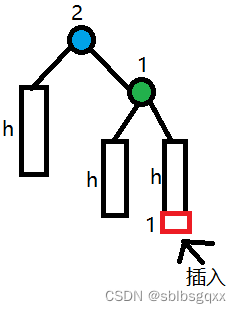
// 左单旋void RotateL(Node* pParent){Node* parent = pParent->_parent;//变成局部的根Node* pParentR = pParent->_right;Node* pParentL = pParentR->_left;//如果pParnet为根,则要修改根if (pParent == _proot)_proot = pParentR;pParent->_right = pParentL;if (pParentL)pParentL->_parent = pParent;pParentR->_left = pParent;pParent->_parent = pParentR;pParentR->_parent = parent;//只需要修改pParent和pParentR的平衡因子pParent->_bf = 0;pParentR->_bf = 0;return;}
旋转之后的情况:
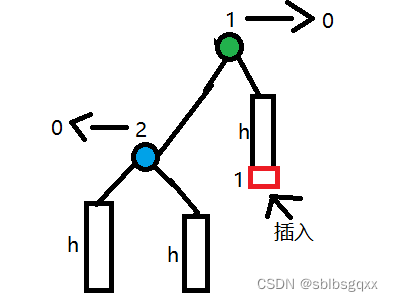
- 左右双旋
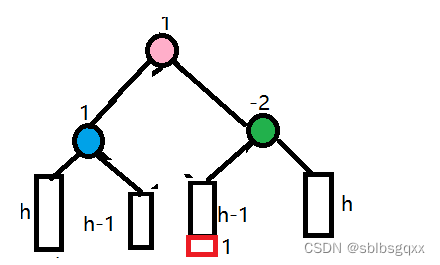
初始情况(插入可以插入到左边或右边,情况不同平衡因子也会不同):
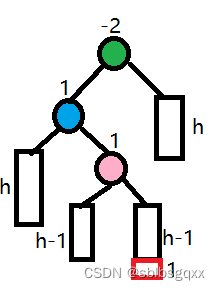
// 左右双旋void RotateLR(Node* pParent){Node* pParentL = pParent->_left;Node* pParentLR = pParentL->_right;int bf = pParentLR->_bf;RotateL(pParentL);RotateR(pParent);if (bf == 0){pParent->_bf = 0;pParentL->_bf = 0;pParentLR->_bf = 0;}else if (bf == 1){pParentL->_bf = -1;pParentLR->_bf = 0;pParent->_bf = 0;}else if (bf == -1){pParentL->_bf = 0;pParent->_bf = 1;pParentLR->_bf = 0;}return;}
旋转之后的情况:
- 右左双旋转
初始情况:
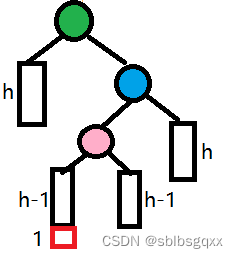
// 右左双旋void RotateRL(Node* pParent){Node* pParnetR = pParent->_right;Node* pParentRL = pParnetR->_left;int bf = pParentRL->_bf;RotateR(pParnetR);RotateL(pParent);if (bf == 0){pParent->_bf = 0;pParnetR->_bf = 0;pParentRL->_bf = 0;}else if (bf == -1){pParent->_bf = 0;pParnetR->_bf = 1;pParentRL->_bf = 0;}else if (bf == 1){pParent->_bf = -1;pParnetR->_bf = 0;pParentRL->_bf = 0;}return;}
旋转之后的情况:
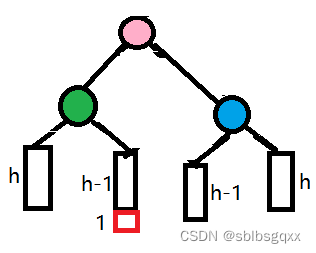
4.AVL树的验证
- 验证为二叉搜索树
中序遍历得到有序的序列就可以证明为二叉搜索树。 - 验证为平衡树
看平衡因子
bool _IsBalance(Node* root, int& height){if (root == nullptr){height = 0;return true;}int leftHeight = 0, rightHeight = 0;if (!_IsBalance(root->_left, leftHeight) || !_IsBalance(root->_right, rightHeight)){return false;}if (abs(rightHeight - leftHeight) >= 2){cout <<root->_kv.first<<"不平衡" << endl;return false;}if (rightHeight - leftHeight != root->_bf){cout << root->_kv.first <<"平衡因子异常" << endl;return false;}height = leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;return true;}

相关文章:

AVL树讲解
AVL树 1. 概念2. AVL节点的定义3. AVL树插入3.1 旋转 4.AVL树的验证 1. 概念 AVL树是一种自平衡二叉搜索树。它的每个节点的左子树和右子树的高度差(平衡因子,我们这里按右子树高度减左子树高度)的绝对值不超过1。AVL的左子树和右子树都是AV…...

20240308-1-校招前端面试常见问题CSS
校招前端面试常见问题【3】——CSS 1、盒模型 Q:请简述一下 CSS 盒模型? W3C 模式:盒子宽widthpaddingbordermargin 怪异模式:盒子宽widthmargin Q:inline、block、inline-block 元素的区别? inline&am…...

linux系统简述docker
简述docker docker理念docker三要素docker平台架构docker运行的基本流程 docker理念 一次镜像,处处运行 基于go语言实现的项目 解决了运行环境和配置问题的软件容器,方便做持续集成并有助于整体发布的容器虚拟化技术 能够使硬件、操作系统和应用程序三者…...

【论文阅读】Mamba:选择状态空间模型的线性时间序列建模(一)
文章目录 Mamba:选择状态空间模型的线性时间序列建模介绍状态序列模型选择性状态空间模型动机:选择作为一种压缩手段用选择性提升SSM 选择性SSM的高效实现先前模型的动机选择扫描总览:硬件感知状态扩展 Mamba论文 Mamba:选择状态空间模型的线性时间序列建…...

漏洞复现-蓝凌LandrayOA系列
蓝凌OA系列 🔪 是否利用过 优先级从高到低 发现日期从近到远 公司团队名_产品名_大版本号_特定小版本号_接口文件名_漏洞类型发现日期.载荷格式LandrayOA_Custom_SSRF_JNDI漏洞 LandrayOA_sysSearchMain_Rce漏洞 LandrayOA_Custom_FileRead漏洞...

计算机网络 路由算法
路由选择协议的核心是路由算法,即需要何种算法来获得路由表中的各个项目。 路由算法的目的很明显,给定一组路由器以及连接路由器的链路,路由算法需要找到一条从源路由器到目的路由器的最佳路径,通常,最佳路径是由最低…...
【C++ 学习】构造函数详解!!!
1. 类的6个默认成员函数的引入 ① 如果一个类中什么成员都没有,简称为空类。 ② 空类中真的什么都没有吗?并不是,任何类在什么都不写时,编译器会自动生成以下6个默认成员函数。 ③ 默认成员函数:用户没有显式实现&…...
——代码随想录算法训练营Day55)
【LeetCode】72. 编辑距离(中等)——代码随想录算法训练营Day55
题目链接:72. 编辑距离 题目描述 给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。 你可以对一个单词进行如下三种操作: 插入一个字符删除一个字符替换一个字符 示例 1: 输入:w…...
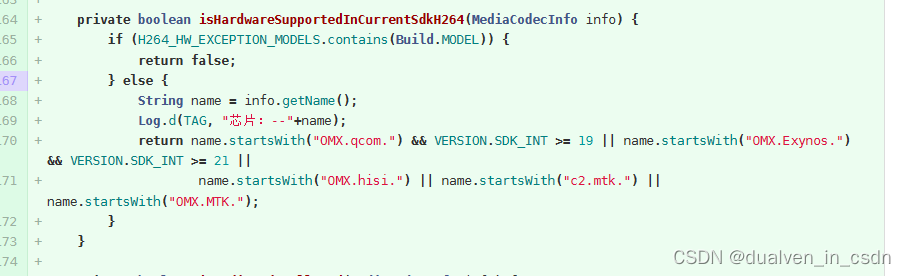
关于手机是否支持h264的问题的解决方案
目录 现象 原理 修改内容 现象 开始以为是手机不支持h264的编码 。机器人chatgpt一通乱扯。 后来检查了下手机,明显是有h264嘛。 终于搞定,不枉凌晨三点起来思考 原理 WebRTC 默认使用的视频编码器是VP8和VP9,WebRTC内置了这两种编码器…...
借助Aspose.html控件,在 Java 中将 URL 转换为 PDF
如果您正在寻找一种将实时 URL 中的网页另存为 PDF文档的方法,那么您来对地方了。在这篇博文中,我们将学习如何使用 Java 将 URL 转换为 PDF。从实时 URL转换HTML网页可以像任何其他文档一样保存所需的网页以供离线访问。将网页保存为 PDF 格式可以轻松突…...
数据结构——堆的应用 堆排序详解
💞💞 前言 hello hello~ ,这里是大耳朵土土垚~💖💖 ,欢迎大家点赞🥳🥳关注💥💥收藏🌹🌹🌹 💥个人主页&#x…...
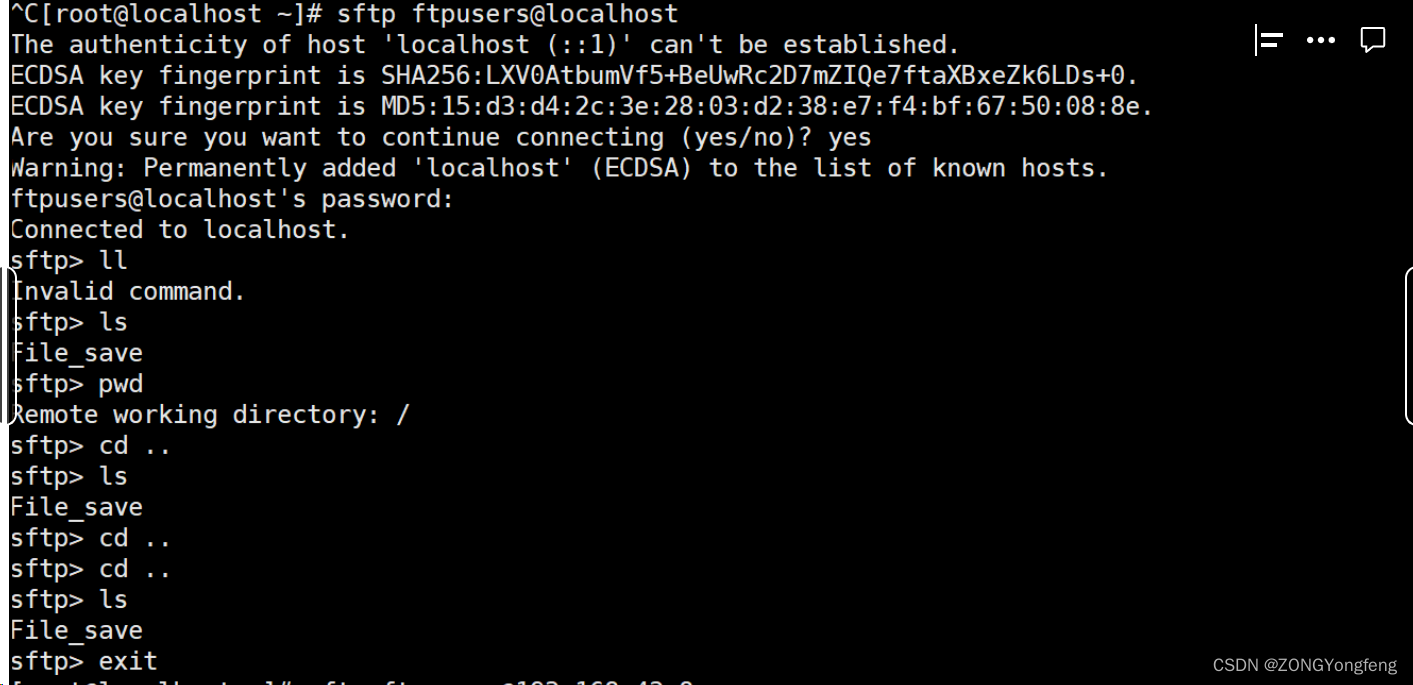
Sftp服务器搭建(linux)
Sftp服务器搭建(linux) 一、基本工作原理 FTP的基本工作原理如下: 1)建立连接:客户端与服务器之间通过TCP/IP建立连接。默认情况下,FTP使用端口号21作为控制连接的端口。 2)身…...
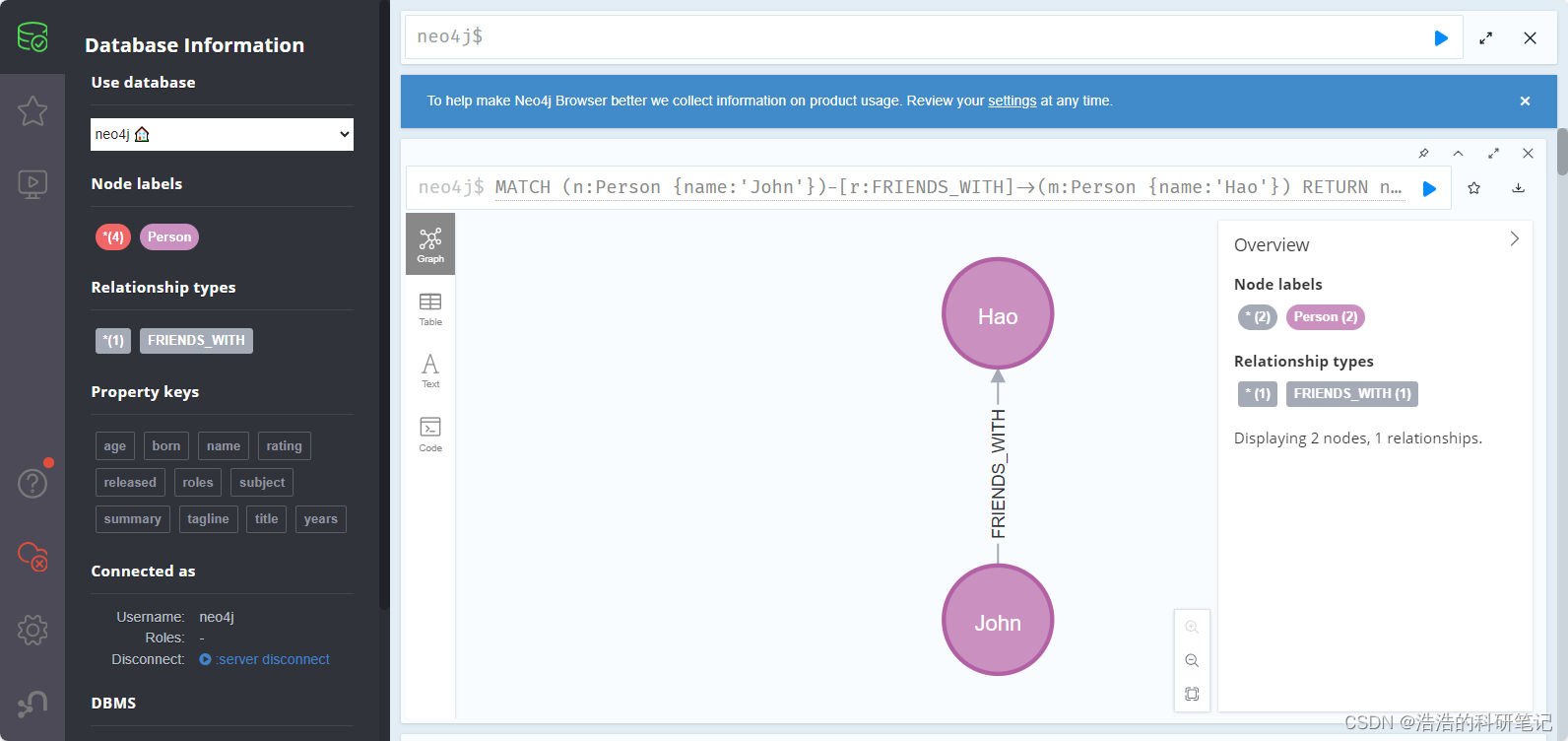
Neo4j 新手教程 环境安装 基础增删改查 python链接 常用操作 纯新手向
Neo4j安装教程🚀 目前在学习知识图谱的相关内容,在图数据库中最有名的就是Neo4j,为了降低入门难度,不被网上很多华丽呼哨的Cypher命令吓退,故分享出该文档,为自己手动总结,包括安装环境,增删改查…...
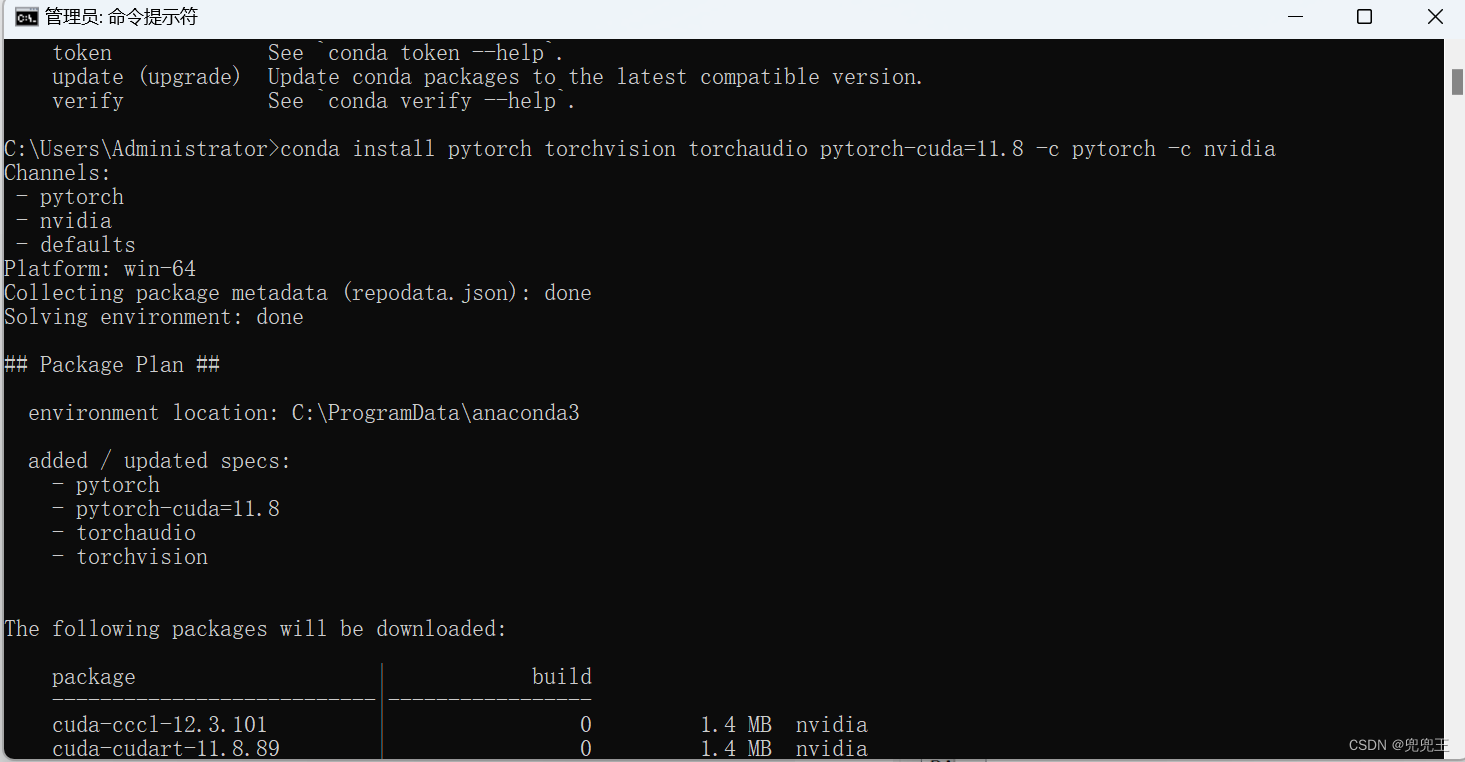
PyTorch2.0 环境搭建详细步骤(Nvidia显卡)
Step 1 、查看显卡驱动版本 Step2、下载CUDA 11.7 或者11.8(我自己用的这个)也行,稍后我会贴出来版本匹配对应表 https://developer.nvidia.com/cuda-toolkit-archive Step3、下载CUDNN cuDNN 9.0.0 Downloads | NVIDIA Developer Step4、安装anconda&…...

Python逆向:pyc字节码转py文件
一、 工具准备 反编译工具:pycdc.exe 十六进制编辑器:010editor 二、字节码文件转换 在CTF中,有时候会得到一串十六进制文件,通过010editor使用查看后,怀疑可能是python的字节码文件。 三、逆向反编译 将010editor得到…...

提示词工程技术:类比、后退、动态少样本、自动生成CoT
类比提示 “类比提示”利用类比推理的概念,鼓励模型生成自己的例子和知识,从而实现更灵活和高效的解决问题。 后退提示 “后退提示”专注于抽象,引导模型推导出高级概念和原理,进而提高其推理能力。 使用一个基本的数学问题来…...

【深度学习笔记】6_5 RNN的pytorch实现
注:本文为《动手学深度学习》开源内容,部分标注了个人理解,仅为个人学习记录,无抄袭搬运意图 6.5 循环神经网络的简洁实现 本节将使用PyTorch来更简洁地实现基于循环神经网络的语言模型。首先,我们读取周杰伦专辑歌词…...
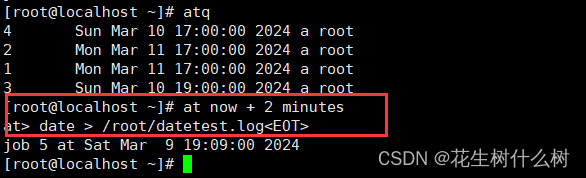
Linux at任务调度命令行编辑错误
错误: 在at任务调度命令行语句编辑错误时,按backspace进行删除无法进行。 解决方案: 请按Ctrlbackspace进行删除,即可解决。...

lua与C++粘合层框架
lua调用C++ 在lua中是以函数指针的形式调用函数, 并且所有的函数指针都必须满足如下此种类型: typedef int (*lua_CFunction) (lua_State *L); 也就是说, 偶们在C++中定义函数时必须以lua_State为参数, 以int为返回值才能被Lua所调用. 但是不要忘记了, 偶们的lua_State是支…...

POST 请求,Ajax 与 cookie
POST 请求则需要设置RequestHeader告诉后台传递内容的编码方式以及在 send 方法里传入对应的值 xhr.open("POST", url, true); xhr.setRequestHeader(("Content-Type": "application/x-www-form-urlencoded")); xhr.send("key1value1&…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...
