动态规划6,最大数组和,环形子数组最大和,乘积最大子数组
最大子数组和

思路:
1.经验+题目要求
dp[i]表示:以 i 位置为结尾的所有子数组中的最大和
2.状态转移方程
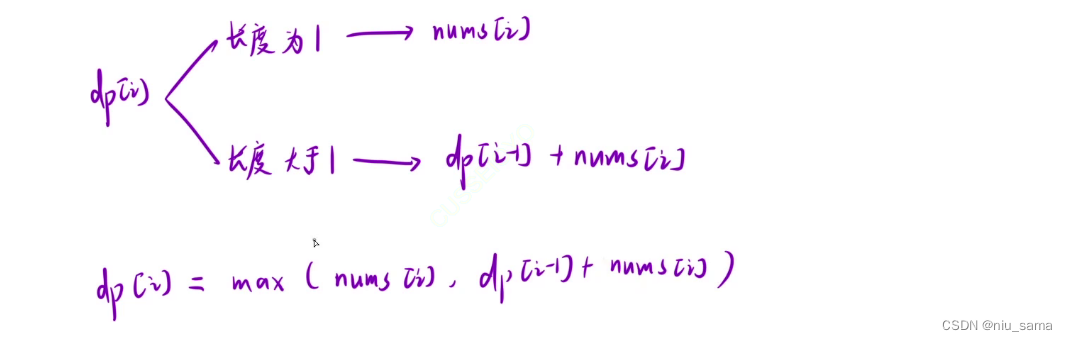
按长度来划分,如果长度为1,那么dp[i] = nums[i];
如果长度大于1,那么当前位置的最大和就为 i-1 位置最大和 + 当前位置,dp[i] = dp[i-1] + nums[i];
然后每一次都要取他们两个中的最大值。
存在 dp[i-1] , 建表时候多建一格,dp[0]位置为0 就不影响后面的填表

4 .
从左往右填表。
class Solution {
public:int maxSubArray(vector<int>& nums) {int n = nums.size();vector<int> dp(n+1);int ret = INT_MIN;//为了不影响比较for(int i = 1 ; i<=n; i++){dp[i] = max(nums[i-1],dp[i-1]+nums[i-1]);ret = max(dp[i],ret);//找出dp表里面的最大值}return ret;}
};
环形子数组的最大和

思路:
区别于上一道题,这一题变成了环形,也就是多了两边的情况,而两边的情况很复杂,我们可不可以把两边问题换为两种上一道题思路的简单问题?
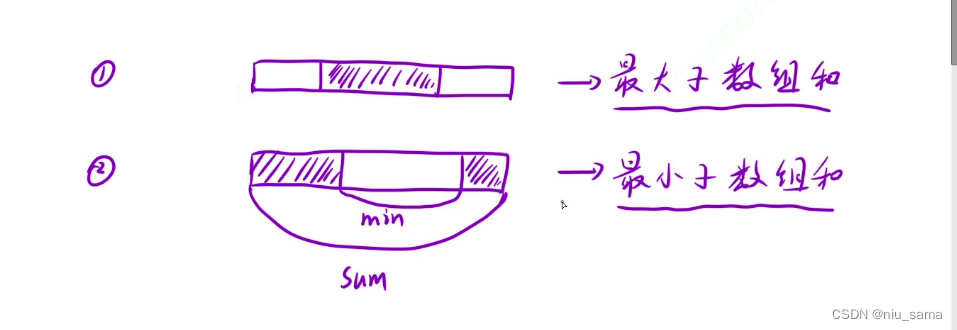
最大数组和只有两种情况,看 1 在里面的情况,这就跟上一道题一样
看 2 ,当最大数组和在两边的时候,我们可以求出最小数组和的情况,然后sum - min。
步骤及思路都跟上一题一样,无非变成了求一个最大和表和一个最小和表,然后比较max(最大和,sum-最小和);
但是对于返回值,有点变化:

对于[-2 , -3 , -1], 最大和为-1, 但是最小和为-2 + -3 + -1 ,和sum是一样的,这时候最小和就变为了错误的0;
所以对于返回值要处理, 最小和 == sum的时候,返回最大和,不然返回max(最大和,sum-最小和)。
class Solution {
public:int maxSubarraySumCircular(vector<int>& nums) {int n = nums.size();vector<int> f(n+1);//建表auto g = f;int ret1 = INT_MIN;//不影响比较int ret2 = INT_MAX;int num = 0;for(int i = 1; i<=n; i++){f[i] = max(nums[i-1],f[i-1]+nums[i-1]);ret1 = max(ret1,f[i]);g[i] = min(nums[i-1],g[i-1]+nums[i-1]);ret2 = min(ret2,g[i]);num+=nums[i-1]; //求nums和}return num == ret2 ? ret1 : max(ret1,num - ret2);}
};
乘积最大子数组

思路:
1.经验+题目要求
dp[i]表示:以 i 位置为结尾的所有子数组中的最大乘积
2.状态转移方程
按长度来划分,如果长度为1,那么dp[i] = nums[i];
如果长度大于1,那么当前位置的最大和就为 i-1 位置最大和 + 当前位置,dp[i] = dp[i-1] * nums[i];
但是因为有正负,前面可能还是乘积最大,后一个数为负数,一下就变成了乘积最小;
相反,前面乘积最小,后一个数为负数,一下就就变成了乘积最大。
所以也要建一个乘积最小表。

f 表是乘积最大表,g 表是乘积最小表,
对于 f 表来讲,如果长度为1,f[i] = nums[i];
如果长度大于1,但是下一个数大于0,那么f[i] = f[i-1] * nums[i];
如果长度大于1,但是下一个数小于0,那么f[i] = g[i-1] * nums[i];
比较这三者的最大值并填入 f 表即可。 g表同理。

为了不影响乘积之间的填表,初始化f[0] = g[0] = 1就可以。
4.从左往右,两个表一起填写。
class Solution {
public:int maxProduct(vector<int>& nums) {int n = nums.size();vector<int> f(n+1);auto g = f;int ret1 = INT_MIN;int ret2 = INT_MAX;f[0] = g[0] = 1;for(int i = 1; i<=n; i++){f[i] = max(nums[i-1],max(f[i-1]*nums[i-1], g[i-1]*nums[i-1]));ret1 = max(f[i],ret1);g[i] = min(nums[i-1],min(g[i-1]*nums[i-1], f[i-1]*nums[i-1]));ret2 = min(g[i],ret2);}return ret1;}
};
乘积为正数的最长子数组长度

思路:
1.经验+题目要求
dp[i]表示:以 i 位置为结尾的所有子数组中乘积为正数的最长长度。
2.状态转移方程
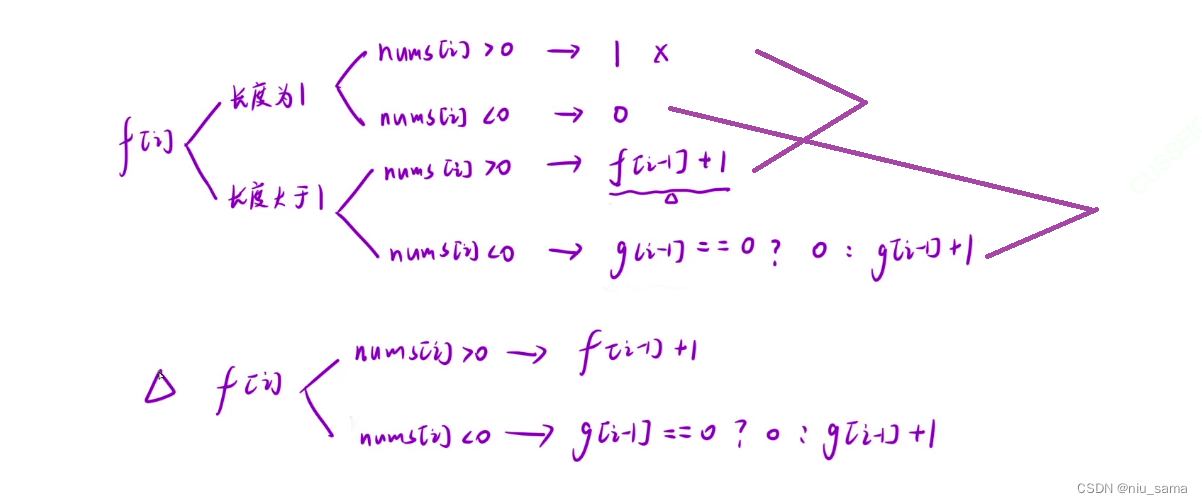
首先细分,当长度为1的时候,如果nums[i] > 0 ,则为1;
当长度为1的时候,如果nums[i] < 0 ,则为0;
当长度大于1的时候,如果nums[i] > 0 ,则为f[i-1] + 1;
当长度大于1的时候,如果nums[i] < 0 ,则为g[i-1] + 1;但是这个g[i-1] + 1真的对吗?当g[i-1] 为0的时候,也就是前面乘积为正数,乘完nums[i] 后长度就变成0了,但是g[i-1] + 1结果为1,明显是错误的,所以应该判断 g[i-1] == 0 ? 0 : g[i-1] + 1;
再次划分情况,对于nums[i] > 0 的情况,f[i-1] + 1最次也为1,占主导;
对于nums[i] < 0 的情况,g[i-1] == 0 ? 0 : g[i-1] + 1;最次也为0,占主导;
就可以总结为下面那两种占主导的情况。
g[i] 也是如此。
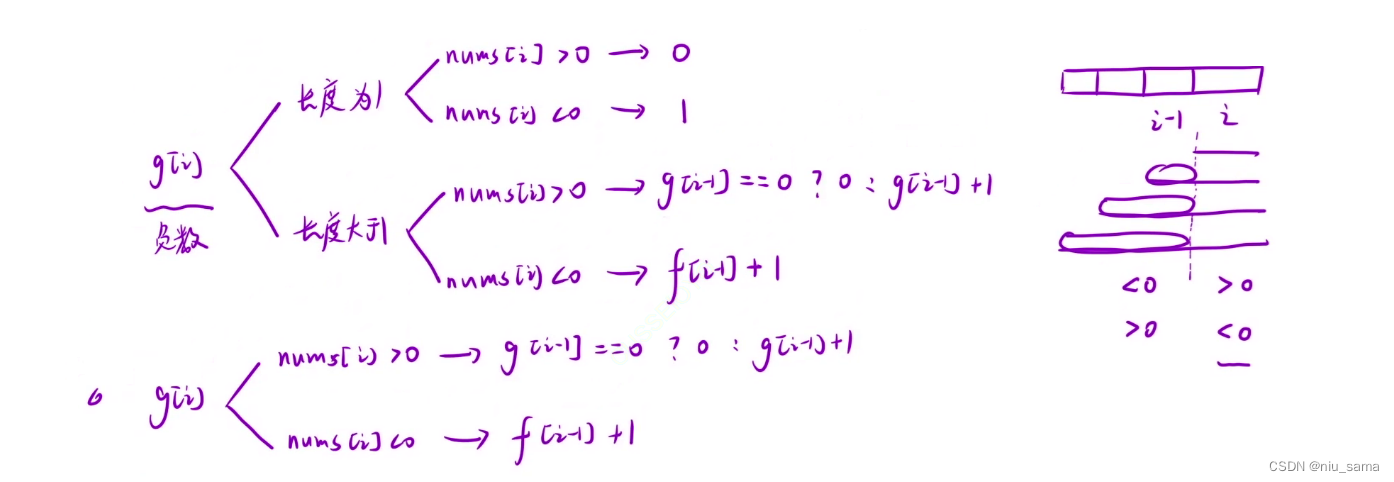
3.
因为题目问的是长度,初始化f[0] = g[0] = 0;

4.从左往右,两个表一起填写。
class Solution {
public:int getMaxLen(vector<int>& nums) {int n = nums.size();vector<int> f(n+1);auto g = f;int ret = INT_MIN;for(int i =1; i<=n; i++){if(nums[i-1] > 0){f[i] = f[i-1]+1;g[i] = g[i-1] == 0 ? 0 : g[i-1]+1;}else if(nums[i-1] < 0){f[i] = g[i-1] == 0 ? 0 : g[i-1]+1;g[i] = f[i-1]+1;}ret = max(ret,f[i]);}return ret;}
};
相关文章:

动态规划6,最大数组和,环形子数组最大和,乘积最大子数组
最大子数组和 思路: 1.经验题目要求 dp[i]表示:以 i 位置为结尾的所有子数组中的最大和 2.状态转移方程 按长度来划分,如果长度为1,那么dp[i] nums[i]; 如果长度大于1,那么当前位置的最大和就为 i-1 位置最大和 …...
js 清空数组的方法
1、直接赋值空数组 let array [1, 2, 3, 4, 5]; array []; 这种方法并不推荐,如下图所示: 虽然a数组确实变为了空数组,但这种方法只是修改了a的指向,把a指向一个新的空数组,然而[1,2,3,4,5]这个数组并没有被清除&a…...
QT中使用QProcess执行命令,实时获取数据,例如进度条
前言 因为之前写了一个接收和发送文件的脚本,然后又需要获取进度,同步到进度条中。 效果: 使用正则匹配,获取命令行命令中的以下数据,然后同步到进度条 源码demo: 非完整代码: #include <Q…...
绘图设计:用Draw.io绘制图形技巧大全(含统一建模语言UML模板)
一、常见UML模板 1.流程图 2.用例图 include是包含关系,extend是扩展关系 简而言之,include是子集指向父集;而extend是扩展用例指向基础用例(基础用例可以理解为系统核心功能,扩展用例是可选的,不是必须…...

被唤醒的“第二十条”深入人心
近来张艺谋执导的电影《第二十条》,因为它与正在召开中的全国两会所发布的《最高人民法院工作报告》联系相当紧密,加之可免费收看,网民便相互转告,于是此信息条目立即冲上了网络热搜榜,观者如潮。因为最高人民法院工作…...
信息泄漏原理以及修复方法)
PHPInfo()信息泄漏原理以及修复方法
漏洞名称:PHPInfo信息泄漏、phpinfo()函数信息泄漏 漏洞描述: phpinfo()函数返回的信息中包含了服务器的配置信息,包括: 1)PHP编译选项以及文件扩展名的相关信息; 2)php的版本信息 3&#…...

202441读书笔记|《笠翁对韵》—— 金菡萏,玉芙蓉,酒晕微酡琼杏颊,香尘浅印玉莲双
202441读书笔记|《笠翁对韵》——金菡萏,玉芙蓉,酒晕微酡琼杏颊,香尘浅印玉莲双 《作家榜名著:笠翁对韵》作者李渔,霍俊明。是所有词句都有注音的一本书,轻松学不认识的字,非常朗朗上口的对偶词…...

006-v-model原理
v-model原理 简介v-model应用在输入框上v-model应用在组件上 简介 由 属性绑定(v-bind:value“searchText”) 配合 input事件监听(v-on:input“searchText event.target.value”) 实现。 应用在组件上由 props: {value: xxx } ,this.$emit(‘input’, xxx ) 完成。…...

Ubuntu下使用DAPLink(OpenOCD)
目录 1. 下载OpenOCD源代码 2. 编译代码 2.1 运行bootstrap 2.2 安装关联库 2.3 运行./configure 2.4 运行make 2.5 运行sudo make install 3. 烧录程序 3.1 挂起MCU 3.2 写入镜像 3.3 校验镜像 通过OpenOCD实现,在Ubuntu18 64bit下验证。 1. 下载OpenOC…...
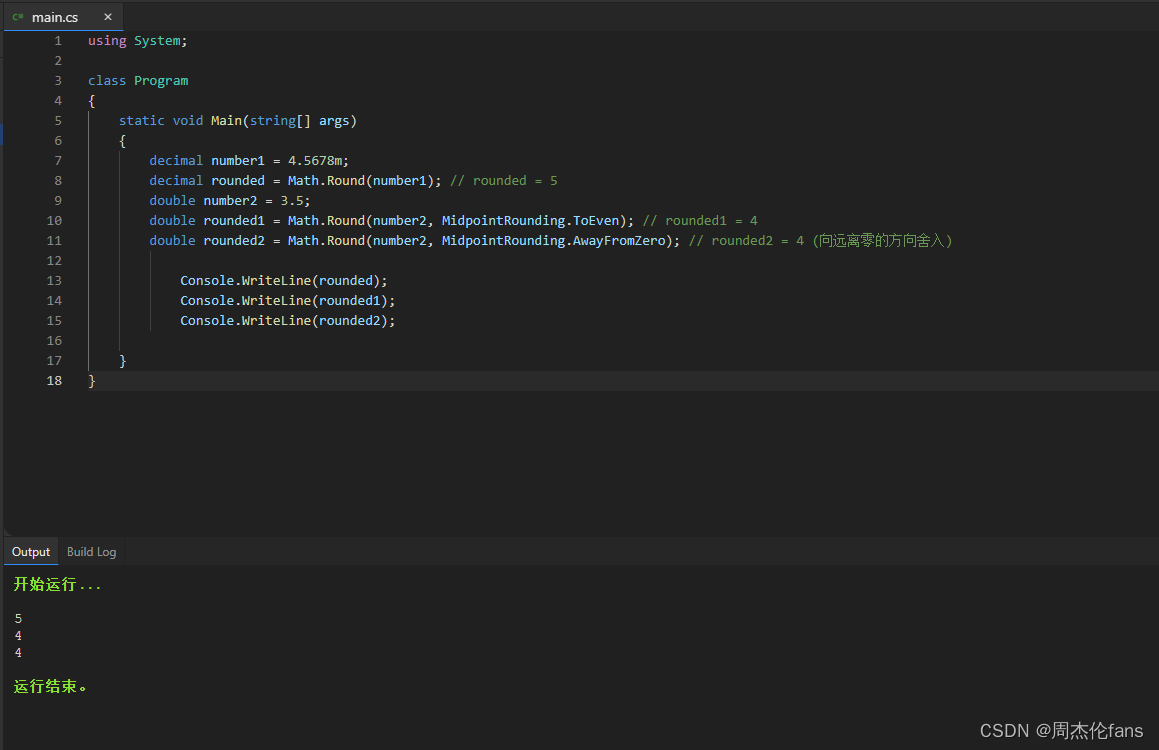
C# 中 Math.Round 数学函数
在 C# 中,Math.Round 是一个数学函数,用于对一个浮点数进行四舍五入操作。它接受一个浮点数作为输入,并返回一个最接近输入值的整数或指定小数位数的浮点数。 Math.Round 方法有多个重载,其中最常用的重载有以下两种形式…...

力扣---接雨水---单调队列
题目: 单调队列思想: 没有思路的小伙伴可以先把这个想清楚哦:力扣hot10---大根堆双端队列-CSDN博客 从上面的图就可以发现,如果柱子呈递减序列,那么不会接到雨水,只要有一个小凸起柱子,那么这个…...

微分学<4>——微分中值定理
索引 微分中值定理极值定义4.1 极大(小)值定理4.1 Fermat引理定理4.2 Rolle定理 Lagrange中值定理定理4.3 Lagrange中值定理定理4.4 Cauchy中值定理 导数对函数性质的刻画Jensen不等式 微分中值定理 极值 定义4.1 极大(小)值 若存在 x 0 x_{0} x0的邻域 U ( x 0 , δ ) U\…...
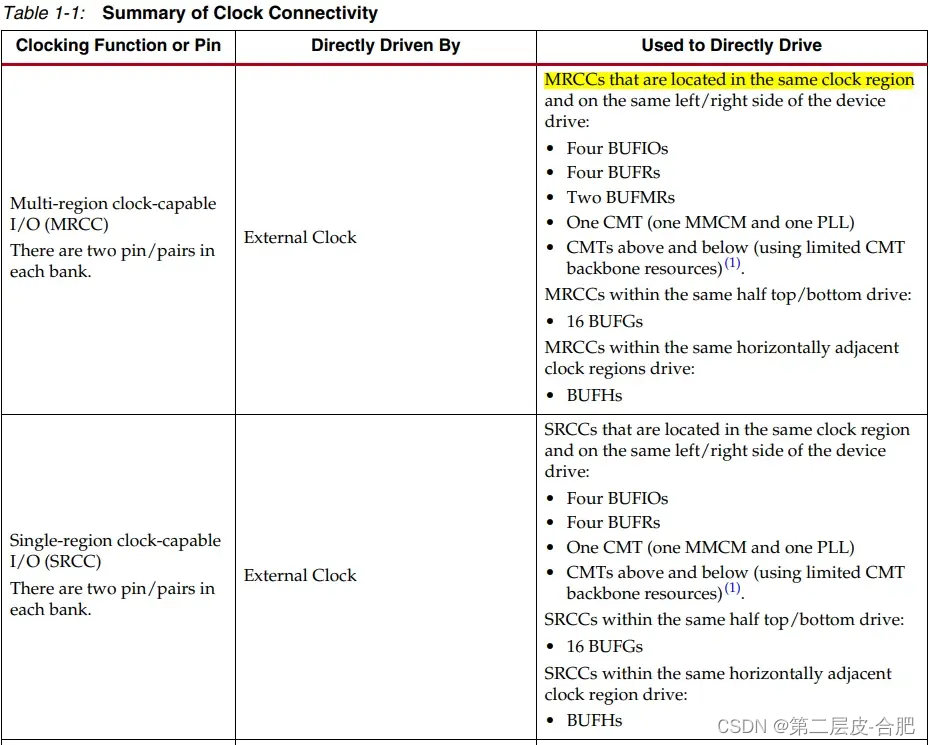
FPGA的时钟资源
目录 简介 Clock Region详解 MRCC和SRCC的区别 BUFGs 时钟资源总结 简介 7系列FPGA的时钟结构图: Clock Region:时钟区域,下图中有6个时钟区域,用不同的颜色加以区分出来 Clock Backbone:从名字也能看出来&#x…...

LeetCode27: 移除元素
题目描述 给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。 不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。 元素的顺序可以改变。你不需要考虑数组中超出…...

Python使用Beautiful Soup及解析html获取元素并提取内容值
Python使用Beautiful Soup及解析html获取元素并提取内容值 1. 包括解析获取标题2. 根据标签及id获取所有元素3. 根据标签及class获取所有元素4. 获取元素下的标签的值5. 获取元素下的parent及child的元素的值参考 1. 包括解析获取标题 2. 根据标签及id获取所有元素 3. 根据标…...

如何清除keep-alive缓存
在 Vue.js 中,使用 <keep-alive> 组件可以将组件保留在内存中,以避免重复渲染和销毁,从而提高性能。如果需要手动清除 <keep-alive> 组件的缓存,可以通过两种方法来实现: 通过 $destroy 方法销毁组件&…...
2024年新手视频剪辑软件推荐-6款视频剪辑软件测评
视频剪辑软件推荐 premiere premiere 直达地址:各大软件网站 说到底,还是得专业的来,虽然很多人觉得他是收费的,但是你懂的,想要免费总是会有办法的.别的不说,剪辑这块,我还是很认可这个软件,虽然我现在还是刚入门. 剪映 剪映 抖音官方推出的一款手机视频编辑剪辑应用,提供切割…...

无货源抖店可以做吗?那些月入上万是真的吗?分享我的成功秘籍
大家好,我是电商花花。 现在还是有人在不停的在问,抖音小店无货源还可以做吗?那些月入上万都是真的吗? 当然是真的,而且做抖音小店非常简单,前提是你真的完全掌握到核心玩法,且要有执行力。 …...

文献阅读:DEA-Net:基于细节增强卷积和内容引导注意的单图像去雾
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 摘要Abstract文献阅读:DEA-Net:基于细节增强卷积和内容引导注意的单图像去雾1、研究背景2、方法提出3、相关知识3.1、DEConv3.3、多重卷积的…...

2024想要赚点小钱真的很容易!帮你们找的10个搞钱第二职业
我们都希望在空闲时间里增加一些额外收入,并有机会找到自己热爱的事业,每天贝兼几十上百元是一个不错的开始,小钱也是钱, 搞钱的经验会积少成多。今天分享10个搞钱第二职业,2024想要赚点小钱真的很容易。 一.摆摊卖花 …...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...
