微分学<4>——微分中值定理
索引
- 微分中值定理
- 极值
- 定义4.1 极大(小)值
- 定理4.1 Fermat引理
- 定理4.2 Rolle定理
- Lagrange中值定理
- 定理4.3 Lagrange中值定理
- 定理4.4 Cauchy中值定理
- 导数对函数性质的刻画
- Jensen不等式
微分中值定理
极值
定义4.1 极大(小)值
若存在 x 0 x_{0} x0的邻域 U ( x 0 , δ ) U\left ( x_{0}, \delta \right ) U(x0,δ),使得 ∀ x ∈ U ( x 0 ) , δ \forall x\in U\left ( x_{0}\right), \delta ∀x∈U(x0),δ, f ( x ) ≤ f ( x 0 ) f\left(x\right ) \le f\left(x_{0}\right ) f(x)≤f(x0),则称 x 0 x_{0} x0是函数 f ( x ) f\left(x\right ) f(x)的一个极大值点。
若存在 x 0 x_{0} x0的邻域 U ( x 0 , δ ) U\left ( x_{0}, \delta \right ) U(x0,δ),使得 ∀ x ∈ U ( x 0 ) , δ \forall x\in U\left ( x_{0}\right), \delta ∀x∈U(x0),δ, f ( x ) ≥ f ( x 0 ) f\left(x\right ) \ge f\left(x_{0}\right ) f(x)≥f(x0),则称 x 0 x_{0} x0是函数 f ( x ) f\left(x\right ) f(x)的一个极小值点。
定理4.1 Fermat引理
设 x 0 x_{0} x0是函数 f ( x ) f\left(x\right ) f(x)的一个极值点,且函数 f ( x ) f\left(x\right ) f(x)在点 x 0 x_{0} x0处可导,则 f ′ ( x 0 ) = 0 f^{\prime }\left ( x_{0} \right )=0 f′(x0)=0。
不妨设 x 0 x_{0} x0是函数 f ( x ) f\left(x\right ) f(x)的一个极大值点。
令 Δ x ∈ ( 0 , δ ) \Delta x\in \left ( 0,\delta \right ) Δx∈(0,δ),则 f ( x 0 + Δ x ) − f ( x 0 ) Δ x ≤ 0 \frac{f\left ( x_{0}+\Delta x \right )-f\left ( x_{0} \right ) }{\Delta x} \le 0 Δxf(x0+Δx)−f(x0)≤0,
根据函数极限的保不等号性, f + ′ ( x 0 ) = lim x 0 + → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x ≤ 0 f^{\prime } _{+}\left ( x_{0} \right ) =\lim_{x_{0}^{+} \to 0} \frac{f\left ( x_{0}+\Delta x \right )-f\left ( x_{0} \right ) }{\Delta x}\le 0 f+′(x0)=limx0+→0Δxf(x0+Δx)−f(x0)≤0;
同理令 Δ x ∈ ( − δ , 0 ) \Delta x\in \left ( -\delta,0 \right ) Δx∈(−δ,0),则 f − ′ ( x 0 ) = lim x 0 − → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x ≥ 0 f^{\prime } _{-}\left ( x_{0} \right ) =\lim_{x_{0}^{-} \to 0} \frac{f\left ( x_{0}+\Delta x \right )-f\left ( x_{0} \right ) }{\Delta x}\ge 0 f−′(x0)=limx0−→0Δxf(x0+Δx)−f(x0)≥0,
因为函数 f ( x ) f\left(x\right ) f(x)在点 x 0 x_{0} x0处可导,所以函数 f ( x ) f\left(x\right ) f(x)在点 x 0 x_{0} x0处 f + ′ ( x 0 ) = f − ′ ( x 0 ) = f ′ ( x 0 ) = 0 f^{\prime } _{+}\left ( x_{0} \right ) =f^{\prime } _{-}\left ( x_{0} \right ) =f^{\prime }\left ( x_{0} \right )=0 f+′(x0)=f−′(x0)=f′(x0)=0。
定理4.2 Rolle定理
函数 f ( x ) f\left ( x \right ) f(x)在闭区间 [ a , b ] \left [ a,b \right ] [a,b]上连续,在开区间 ( a , b ) \left ( a,b \right ) (a,b)上可导, f ( a ) = f ( b ) f\left ( a \right )=f\left ( b \right ) f(a)=f(b),则 ∃ ξ ∈ ( a , b ) \exists \xi \in \left ( a,b \right ) ∃ξ∈(a,b): f ′ ( ξ ) = 0 f^{\prime }\left ( \xi \right )=0 f′(ξ)=0。
根据最值定理, f ( x ) f\left ( x \right ) f(x)在 [ a , b ] \left [ a,b \right ] [a,b]上必有最大值 M M M和最小值 m m m,也就是 ∃ η \exists \eta ∃η, ξ ∈ [ a , b ] \xi \in \left [ a,b \right ] ξ∈[a,b]: ∀ x ∈ [ a , b ] \forall x\in \left [ a,b \right ] ∀x∈[a,b], f ( η ) = m = min f ( x ) f\left ( \eta \right )=m= \min f\left ( x \right ) f(η)=m=minf(x), f ( ξ ) = M = max f ( x ) f\left ( \xi \right )=M=\max f\left ( x \right ) f(ξ)=M=maxf(x)。
不妨设函数 f ( x ) f\left ( x \right ) f(x)在闭区间 [ a , b ] \left [ a,b \right ] [a,b]上有最大值 M = f ( ξ ) M=f\left ( \xi \right ) M=f(ξ)。
<1> M = f ( a ) ( = f ( b ) ) M=f\left ( a \right )(=f\left ( b \right )) M=f(a)(=f(b))
此时函数 f ( x ) f\left ( x \right ) f(x)为常数函数,显然 ∃ ξ ∈ ( a , b ) \exists \xi \in \left ( a,b \right ) ∃ξ∈(a,b): f ′ ( ξ ) = 0 f^{\prime }\left ( \xi \right )=0 f′(ξ)=0。
<2> M ≠ f ( a ) ( = f ( b ) ) M\neq f\left ( a \right )(=f\left ( b \right )) M=f(a)(=f(b))
此时 M = f ( ξ ) M=f\left ( \xi \right ) M=f(ξ)为 f ( x ) f\left ( x \right ) f(x)在 [ a , b ] \left [ a,b \right ] [a,b]上的一个极大值, ξ \xi ξ是函数 f ( x ) f\left(x\right ) f(x)的一个极大值点,
根据Fermat引理, f ′ ( ξ ) = 0 f^{\prime }\left ( \xi \right )=0 f′(ξ)=0。
Lagrange中值定理
定理4.3 Lagrange中值定理
函数 y = f ( x ) y=f\left ( x \right ) y=f(x)在闭区间 [ a , b ] \left [ a,b \right ] [a,b]上连续,在开区间 ( a , b ) \left ( a,b \right ) (a,b)上可导,则 ∃ ξ ∈ ( a , b ) \exists \xi \in \left ( a,b \right ) ∃ξ∈(a,b): f ′ ( ξ ) = f ( b ) − f ( a ) b − a f^{\prime } \left ( \xi \right )=\frac{f\left ( b\right ) -f\left ( a \right ) }{b-a} f′(ξ)=b−af(b)−f(a)。
任取 t ∈ ( a , b ) t \in \left ( a,b \right ) t∈(a,b), x = t x=t x=t处切线斜率为 f ′ ( t ) f^{\prime } \left ( t \right ) f′(t)。
另外连接闭区间 [ a , b ] \left [ a,b \right ] [a,b]端点的割线斜率为 k = f ( b ) − f ( a ) b − a k=\frac{f\left ( b \right )-f\left ( a \right ) }{b-a} k=b−af(b)−f(a),割线方程为 y − f ( a ) = ( f ( b ) − f ( a ) b − a ) ( x − a ) y-f\left ( a \right )=\left ( \frac{f\left ( b \right )-f\left ( a \right ) }{b-a} \right )\left ( x-a \right ) y−f(a)=(b−af(b)−f(a))(x−a),
而点 ( t , f ( t ) ) \left (t ,f\left (t \right ) \right ) (t,f(t))到割线 y = ( f ( b ) − f ( a ) b − a ) ( x − a ) y=\left ( \frac{f\left ( b \right )-f\left ( a \right ) }{b-a} \right )\left ( x-a \right ) y=(b−af(b)−f(a))(x−a)的距离函数为 d ( t ) = ∣ k ( t − a ) + f ( a ) − f ( t ) ∣ 1 + k 2 d\left ( t \right )=\frac{\left | k\left ( t-a \right )+f\left ( a \right ) -f\left ( t \right )\right | }{\sqrt{1+k^{2} } } d(t)=1+k2∣k(t−a)+f(a)−f(t)∣, d ′ ( t ) = ∣ k − f ′ ( t ) ∣ 1 + k 2 d^{\prime } \left ( t \right ) =\frac{\left | k-f^{\prime } \left ( t \right ) \right | }{\sqrt{1+k^{2} } } d′(t)=1+k2∣k−f′(t)∣,
因为 d ( t ) d\left ( t \right ) d(t)在闭区间 [ a , b ] \left [ a,b \right ] [a,b]上连续,在开区间 ( a , b ) \left ( a,b \right ) (a,b)上可导,且 d ( a ) = d ( b ) = 0 d \left ( a \right )= d \left ( b \right )=0 d(a)=d(b)=0,所以根据Rolle定理, ∃ ξ ∈ ( a , b ) \exists \xi \in \left ( a,b \right ) ∃ξ∈(a,b): d ′ ( ξ ) = 0 d^{\prime }\left ( \xi \right )=0 d′(ξ)=0,
解方程 d ′ ( ξ ) = ∣ k − f ′ ( ξ ) ∣ 1 + k 2 = 0 d^{\prime }\left ( \xi \right )=\frac{\left | k-f^{\prime } \left ( \xi \right ) \right | }{\sqrt{1+k^{2} } }=0 d′(ξ)=1+k2∣k−f′(ξ)∣=0,可得 f ′ ( ξ ) = k = f ( b ) − f ( a ) b − a f^{\prime } \left ( \xi \right ) =k=\frac{f\left ( b \right )-f\left ( a \right ) }{b-a} f′(ξ)=k=b−af(b)−f(a)。
从几何意义出发,同样根据距离函数 d ( t ) d\left ( t \right ) d(t)的分子部分,可以构造函数 φ ( x ) = f ( x ) − f ( a ) − f ( b ) − f ( a ) b − a ( x − a ) = f ( x ) − f ( a ) − k ( x − a ) \varphi \left ( x \right )=f\left ( x \right )-f\left ( a \right )-\frac{f\left ( b \right )-f\left ( a \right ) }{b-a}\left ( x-a \right )= f\left ( x \right )-f\left ( a \right )-k\left ( x-a \right ) φ(x)=f(x)−f(a)−b−af(b)−f(a)(x−a)=f(x)−f(a)−k(x−a), φ ( x ) \varphi \left ( x \right ) φ(x)仍然满足Rolle定理, ∃ ξ ∈ ( a , b ) \exists \xi \in \left ( a,b \right ) ∃ξ∈(a,b): φ ′ ( ξ ) = 0 \varphi^{\prime } \left ( \xi \right )=0 φ′(ξ)=0,代数方法与几何方法实质上殊途同归。
定理4.4 Cauchy中值定理
函数 y = f ( x ) y=f\left ( x \right ) y=f(x)在闭区间 [ a , b ] \left [ a,b \right ] [a,b]上连续,在开区间 ( a , b ) \left ( a,b \right ) (a,b)上可导,则 ∃ ξ ∈ ( a , b ) \exists \xi \in \left ( a,b \right ) ∃ξ∈(a,b): f ′ ( ξ ) g ′ ( ξ ) = f ( b ) − f ( a ) g ( b ) − g ( a ) ( g ′ ( ξ ) ≠ 0 ) \frac{f^{\prime }\left ( \xi \right ) }{g^{\prime }\left ( \xi \right ) }=\frac{f\left ( b \right )-f\left ( a \right ) }{g\left ( b \right )-g\left ( a \right ) }\left ( g^{\prime}\left ( \xi \right ) \neq 0 \right ) g′(ξ)f′(ξ)=g(b)−g(a)f(b)−f(a)(g′(ξ)=0)。
联立参数方程:
{ y = f ( t ) x = g ( t ) \left\{\begin{matrix} y=f\left ( t \right ) \\ x=g\left ( t \right ) \end{matrix}\right. {y=f(t)x=g(t)
参考Lagrange中值定理,可构造函数 φ ( x ) = f ( x ) − f ( a ) − ( f ( b ) − f ( a ) g ( b ) − g ( a ) ) ( g ( x ) − g ( a ) ) \varphi \left ( x \right )=f\left ( x \right )-f\left ( a \right )-\left ( \frac{f\left ( b \right )-f\left ( a \right ) }{g\left ( b \right )-g\left ( a \right ) } \right ) \left ( g\left ( x \right ) -g\left ( a \right ) \right ) φ(x)=f(x)−f(a)−(g(b)−g(a)f(b)−f(a))(g(x)−g(a)),后续过程与Lagrange中值定理一致。
导数对函数性质的刻画
Jensen不等式
相关文章:

微分学<4>——微分中值定理
索引 微分中值定理极值定义4.1 极大(小)值定理4.1 Fermat引理定理4.2 Rolle定理 Lagrange中值定理定理4.3 Lagrange中值定理定理4.4 Cauchy中值定理 导数对函数性质的刻画Jensen不等式 微分中值定理 极值 定义4.1 极大(小)值 若存在 x 0 x_{0} x0的邻域 U ( x 0 , δ ) U\…...
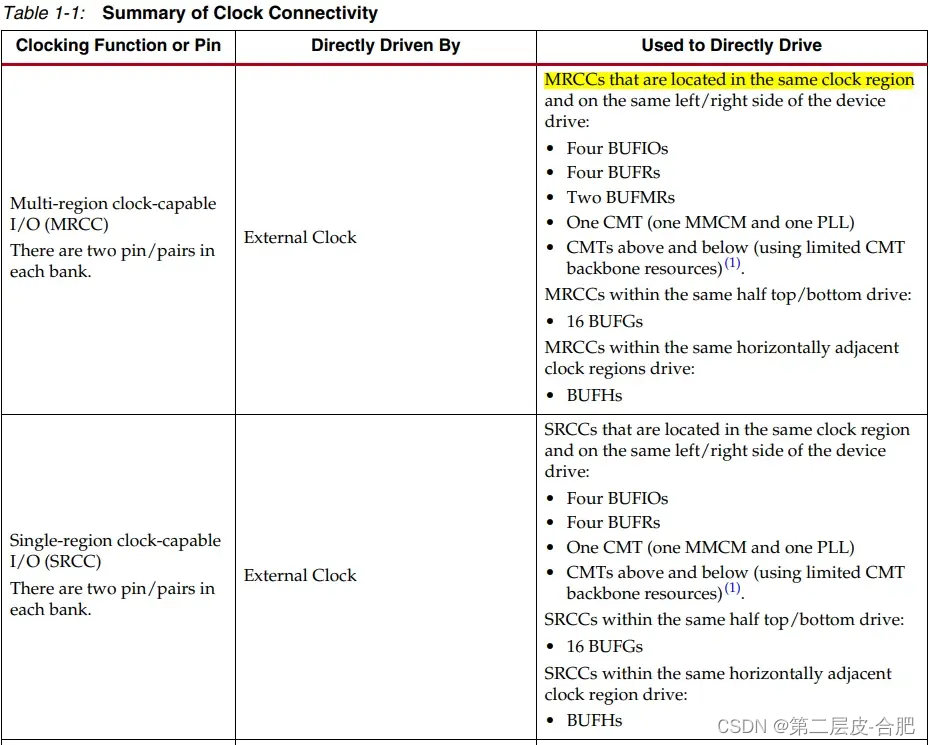
FPGA的时钟资源
目录 简介 Clock Region详解 MRCC和SRCC的区别 BUFGs 时钟资源总结 简介 7系列FPGA的时钟结构图: Clock Region:时钟区域,下图中有6个时钟区域,用不同的颜色加以区分出来 Clock Backbone:从名字也能看出来&#x…...

LeetCode27: 移除元素
题目描述 给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。 不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。 元素的顺序可以改变。你不需要考虑数组中超出…...

Python使用Beautiful Soup及解析html获取元素并提取内容值
Python使用Beautiful Soup及解析html获取元素并提取内容值 1. 包括解析获取标题2. 根据标签及id获取所有元素3. 根据标签及class获取所有元素4. 获取元素下的标签的值5. 获取元素下的parent及child的元素的值参考 1. 包括解析获取标题 2. 根据标签及id获取所有元素 3. 根据标…...

如何清除keep-alive缓存
在 Vue.js 中,使用 <keep-alive> 组件可以将组件保留在内存中,以避免重复渲染和销毁,从而提高性能。如果需要手动清除 <keep-alive> 组件的缓存,可以通过两种方法来实现: 通过 $destroy 方法销毁组件&…...
2024年新手视频剪辑软件推荐-6款视频剪辑软件测评
视频剪辑软件推荐 premiere premiere 直达地址:各大软件网站 说到底,还是得专业的来,虽然很多人觉得他是收费的,但是你懂的,想要免费总是会有办法的.别的不说,剪辑这块,我还是很认可这个软件,虽然我现在还是刚入门. 剪映 剪映 抖音官方推出的一款手机视频编辑剪辑应用,提供切割…...

无货源抖店可以做吗?那些月入上万是真的吗?分享我的成功秘籍
大家好,我是电商花花。 现在还是有人在不停的在问,抖音小店无货源还可以做吗?那些月入上万都是真的吗? 当然是真的,而且做抖音小店非常简单,前提是你真的完全掌握到核心玩法,且要有执行力。 …...

文献阅读:DEA-Net:基于细节增强卷积和内容引导注意的单图像去雾
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 摘要Abstract文献阅读:DEA-Net:基于细节增强卷积和内容引导注意的单图像去雾1、研究背景2、方法提出3、相关知识3.1、DEConv3.3、多重卷积的…...

2024想要赚点小钱真的很容易!帮你们找的10个搞钱第二职业
我们都希望在空闲时间里增加一些额外收入,并有机会找到自己热爱的事业,每天贝兼几十上百元是一个不错的开始,小钱也是钱, 搞钱的经验会积少成多。今天分享10个搞钱第二职业,2024想要赚点小钱真的很容易。 一.摆摊卖花 …...

【Linux网络】再谈 “协议“
目录 再谈 "协议" 结构化数据的传输 序列化和反序列化 网络版计算器 封装套接字操作 服务端代码 服务进程执行例程 启动网络版服务端 协议定制 客户端代码 代码测试 使用JSON进行序列化与反序列化 我们程序员写的一个个解决我们实际问题,满…...

猫头虎分享已解决Bug || 系统监控故障:MonitoringServiceDown, MetricsCollectionError
博主猫头虎的技术世界 🌟 欢迎来到猫头虎的博客 — 探索技术的无限可能! 专栏链接: 🔗 精选专栏: 《面试题大全》 — 面试准备的宝典!《IDEA开发秘籍》 — 提升你的IDEA技能!《100天精通鸿蒙》 …...

Java中的基本数据类型有哪些
在Java编程语言中,基本数据类型(Primitive Types)是预定义的数据类型,它们不是由用户定义的类创建的,而是由语言本身提供的。这些基本数据类型是构成Java程序的基础,用于存储不同类型的值,如整数…...

二叉树遍历(前中后序的递归/非递归遍历、层序遍历)
二叉树的遍历 1. 二叉树的前序、中序、后序遍历 前、中、后序遍历又叫深度优先遍历 注:严格来说,深度优先遍历是先访问当前节点再继续递归访问,因此,只有前序遍历是严格意义上的深度优先遍历 首先需要知道下面几点: …...
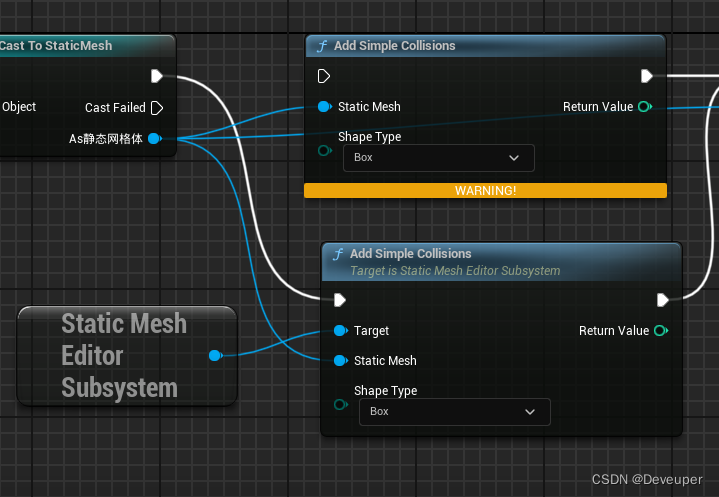
UE4升级UE5 蓝图节点变更汇总(4.26/27-5.2/5.3)
一、删除部分 Ploygon Editing删除 Polygon Editing这个在4.26、4.27中的插件,在5.1后彻底失效。 相关的蓝图,如编辑器蓝图 Generate mapping UVs等,均失效。 如需相关功能,请改成Dynamic Mesh下的方法。 GetSupportedClass删…...
【python】异常处理
前言 省略各种废话,直接快速整理知识点 try-except 基础 作用 程序不可能永远都是对的,当7除a,a由用户输入时,用户输入0就会报错。try-except就是解决这些问题。 结构 多分支自定义错误类型 上方的exception是一个错误类型…...

【xv6操作系统】Lab systems calls
一、实验前须知 阅读 xv6 文档的第 2 章和第 4 章的 4.3 节和 4.4 节以及相关源文件: 系统调用的用户空间代码在 user/user.h 和 user/usys.pl 中。 内核空间代码在 kernel/syscall.h 和 kernel/syscall.c 中。 与进程相关的代码在 kernel/proc.h 和 kernel/proc.c…...

python的scripts文件夹作用
Windows系统: Scripts文件夹通常位于Python的安装目录下,如C:\Python\Scripts。该文件夹内包含了各种有用的工具,例如pip、virtualenv等,这些工具有助于管理和配置Python环境和依赖包。 Linux系统: 在Linux系统中&…...

Discuz论坛网站报错Discuz!Database Error(0)notconnect的解决办法
运营服务器大本营有段时间了,在运营期间遇到两次Discuz!Database Error(0)notconnect报错,和你们分享遇到Discuz报错的解决办法,希望可以帮助到你。 首先网站报错(0)notconnect&…...

掌握mysql,看完这篇文章就够了
数据库 对大量数据进行存储和管理(增删改查) 客户端: 黑窗口终端navicat 熊掌软件数据库分类: 关系型数据库 通过表与表产生关联关系,每个表中都存储结构化数据,支持sql结构化查询语言MysqlOracleSQLS…...

守护Web安全:了解Web攻击与防护策略
🤍 前端开发工程师、技术日更博主、已过CET6 🍨 阿珊和她的猫_CSDN博客专家、23年度博客之星前端领域TOP1 🕠 牛客高级专题作者、打造专栏《前端面试必备》 、《2024面试高频手撕题》 🍚 蓝桥云课签约作者、上架课程《Vue.js 和 E…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...

CSS3相关知识点
CSS3相关知识点 CSS3私有前缀私有前缀私有前缀存在的意义常见浏览器的私有前缀 CSS3基本语法CSS3 新增长度单位CSS3 新增颜色设置方式CSS3 新增选择器CSS3 新增盒模型相关属性box-sizing 怪异盒模型resize调整盒子大小box-shadow 盒子阴影opacity 不透明度 CSS3 新增背景属性ba…...
