Dynamo——常用几何形体的创建与编辑(二)
上一次,我们简单整理了一些创建几何形体的节点用法,今天我们接着整理一些,几何形体的编辑方法。
一、坐标点的平移复制
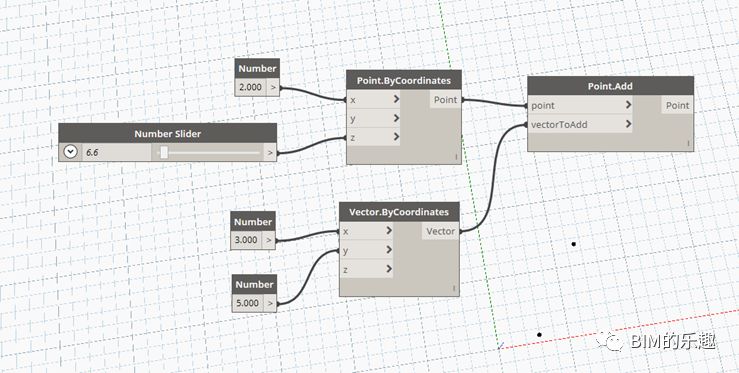
[Point.Add] 使用节点 “Vector.ByCoordinates” 生成一个向量,将该向量连接到 “Point.Add” 节点的输入端 “point”。另将被平移复制的坐标点作为输入项,连接到“point” 输入端,则将输入的坐标点按照向量的方向和长度平移复制。如图所示,输入坐标点为(2,5,0),输入向量为(3,5,0),平移复制后的坐标点为(5,10,0)。
二、几何形体的平移复制
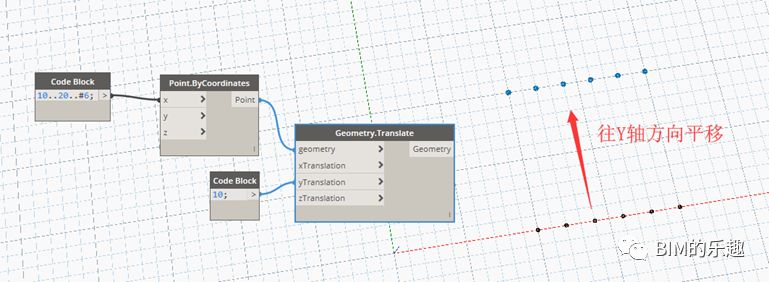
[Geometry.Translate] 在 Dynamo 中,另一个常用的平移复制的节点是
“Geometry.Translate”,适用于所有的几何形体,上例中坐标点的平移复制同样可以使用该节点实现。如下图,输入项分别输入 XYZ 三个方向上平移的坐标分量,即 0,10,0, 将坐标点向 Y 轴方向平移 10 个单位 长度。此节点同样适用于曲线、曲面实体等几何形体的平移复制。
三、几何形体的镜像复制
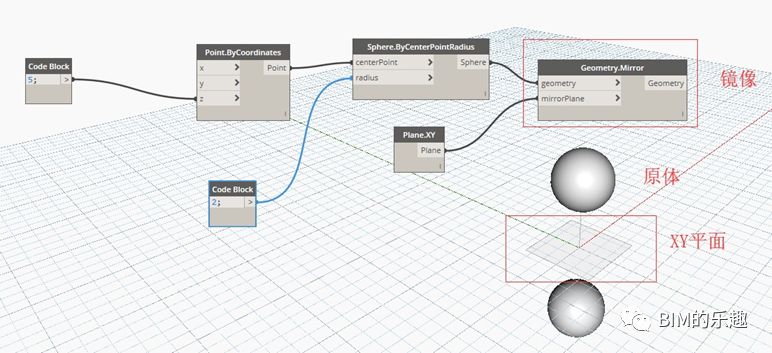
[Geometry.Mirror] 通过输入指定平面,将几何形体根据平面镜像复制。例子中,指定平面为 XY 平面,被镜像的几何形体是球心坐标为(0,0,5),半径为 2 的球体。
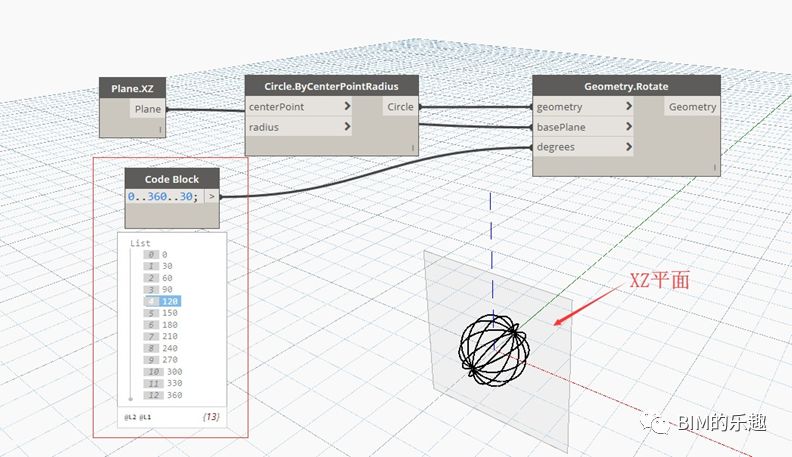
四、几何形体的旋转复制
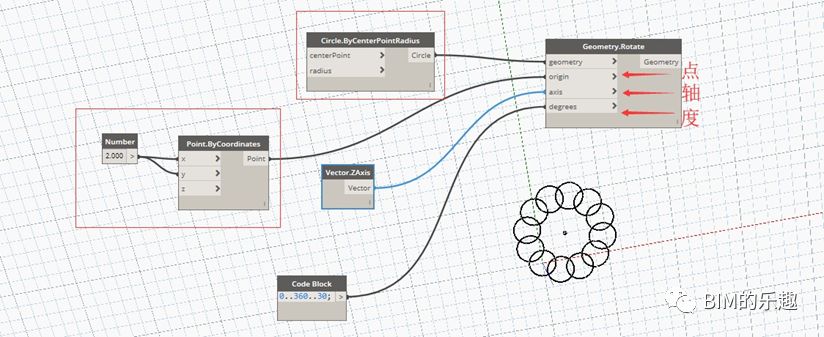
[Geometry.Rotate] “Geometry.Rotate”节点用于几何形体的旋转。输入项包括被旋转的几何形体、绕其旋转的基准坐标点、旋转轴向量、旋转角度。图例中,半径为 1 的圆形,绕基准坐标点 (2,2,0) 旋转,旋转轴为 (0,0,1) 向量,旋转角度为 “0,30,60,90…,360” 的角度列表。
[Geometry.Rotate] 还有另一种形式,输入端为被旋转的几何体、旋转基准面和旋转角度。圆形一 XZ 平面为基准面旋转,生成如图所示的旋转结果。
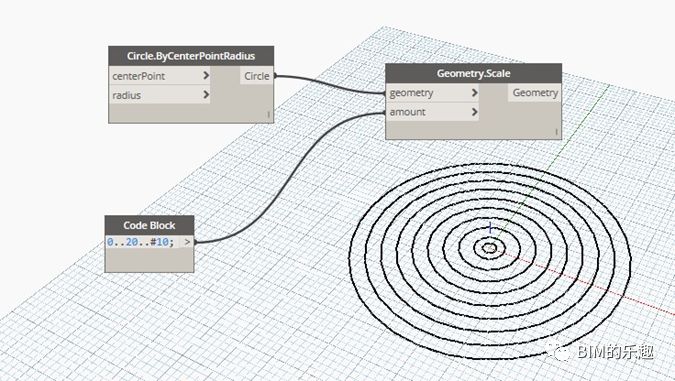
五、几何形体的缩放
[Geometry.Scale] 几何形体的等比例缩放,可以使用节点 “Geometry.Scale”。 输入项为等比例缩放的几何形体以及缩放因子。缩放因子可以是一个数值,也可以是一个数值表。
六、获取几何形体间的距离
[Geometry.DistanceTo] 该节点用于获取几何形体间的空间位置关系,测量两个几何形体间的最短距离。例如图中球心为 (0,0,0), 半径为 3 的球体,距离坐标点(5,0,0) 的距离为 2。测量的是球体表面距坐标点最短的距离。

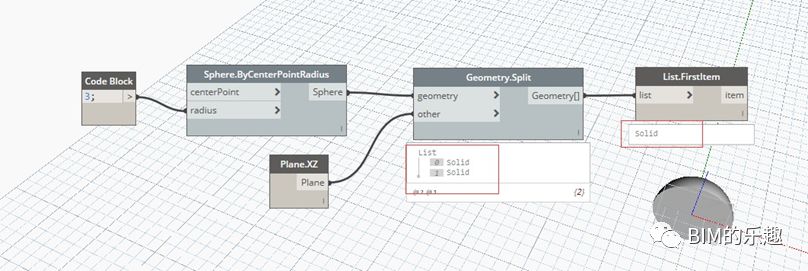
七、几何形体的拆分
[Geometry.Split] 使用任意几何形体(曲线、曲面和实体)对目标几何 形体进行拆分。前提是两个几何形体需要有相交区域。例子中,目标几何形体是球心 (0,0,0), 半径为 3 的球体,作为拆分工具的几何形体是 XZ 平面。则可将球体分割为两个半球,注意“Geometry.Split” 的运算结果是两个 “Solid”。使用“List.FirstItem” 将其中一个 “Solid” 选取出来,隐藏上游节点,则在三维预览视图中,仅显示其中一个半球。
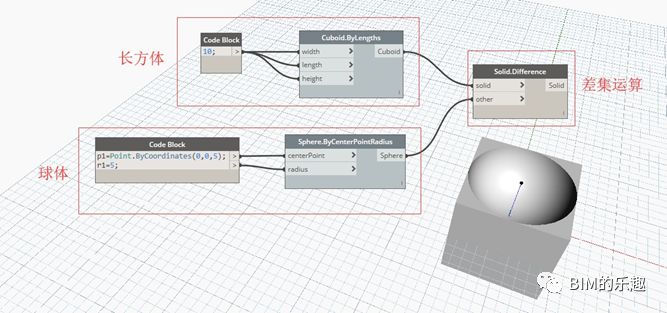
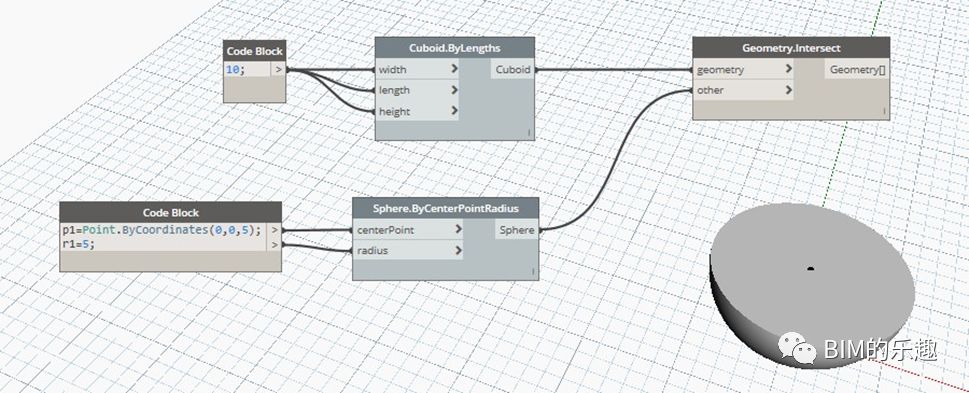
八、几何形体的差集、并基与交集
创建一个长宽高为 10 的立方体,中心坐标为 (0,0,0)。在创建一个球心坐标为 (0,0,5), 半径为 5 的球体。两个几何形体有相交区域,以此为例,进行差集、并集和交集的运算。
[Solid.Difference] 两个几何形体求差集的运算。
[Solid.Union] 两个几何形体求并集的运算。三维视图中显示的是求并集运算后的结果,为一个单一的 “Solid”。

[Geometry.Intersect] 两个几何形体求交集的运算。
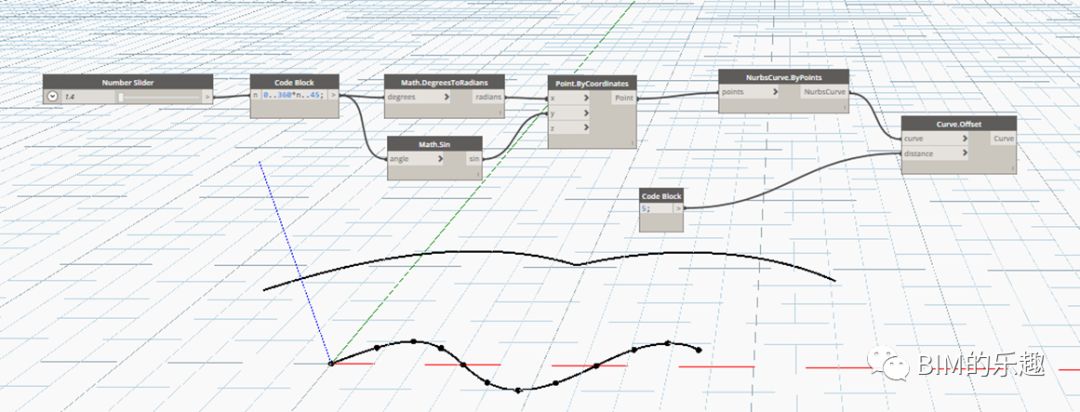
九、曲线的偏移
[Curve.Offset]通过输入偏移距离,将曲线根据默认方向偏移复制。
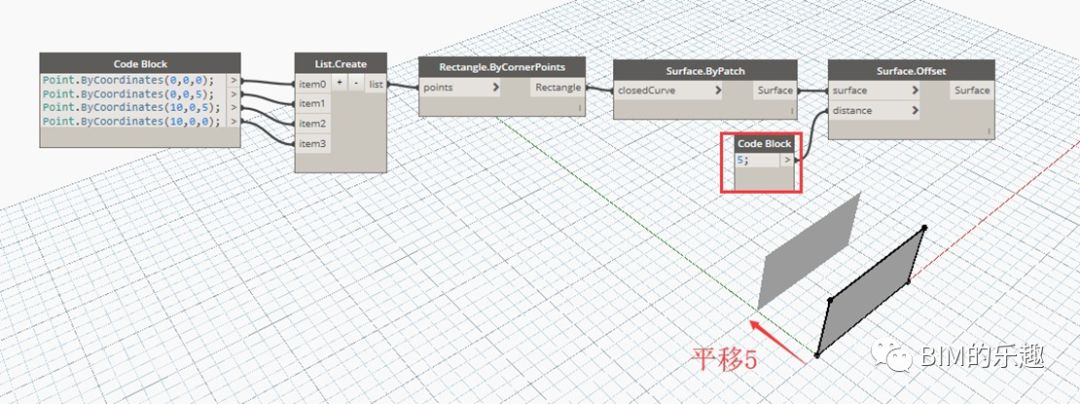
十、曲面的偏移
Surface.Offset]通过输入曲面和偏移距离,将曲面朝曲面法向量方向偏移复制。
最近比较忙,今天就简单整理这十条吧,其实最近关于 Dynamo 的中文资料,网上越来越多了,我只是简单整理一些,方便大家学习!
相关文章:

Dynamo——常用几何形体的创建与编辑(二)
上一次,我们简单整理了一些创建几何形体的节点用法,今天我们接着整理一些,几何形体的编辑方法。 一、坐标点的平移复制 [Point.Add] 使用节点 “Vector.ByCoordinates” 生成一个向量,将该向量连接到 “Point.Add” 节点的输入端 …...
uniapp富文本编辑-editor-vue2-vue3-wangeditor
前言 不管vue2还是vue3,都推荐官方的editor组件, 官方手册 https://uniapp.dcloud.net.cn/component/editor.html除了“微信小程序”,其他小程序想要使用editor组件实现富文本编辑,很难 第三方组件wangeditor在vue2࿰…...

【java】22:try-catch 异常处理
try-catch 方式处理异常说明 public static void main(String[] args) { int num1 10; int num2 0; try { int res num1 / num2; } catch (Exception e) { System.out.println(e.getMessage()); } } 注意事项 1)如果异常发生了,则异常发生后面的代码不会执行&…...

【C语言】linux内核ip_local_out函数
一、讲解 这个函数 __ip_local_out 是 Linux 内核网络子系统中的函数,部分与本地出口的 IPv4 数据包发送相关。下面讲解这段代码的每一部分: 1. 函数声明 int __ip_local_out(struct net *net, struct sock *sk, struct sk_buff *skb): -…...

动态规划6,最大数组和,环形子数组最大和,乘积最大子数组
最大子数组和 思路: 1.经验题目要求 dp[i]表示:以 i 位置为结尾的所有子数组中的最大和 2.状态转移方程 按长度来划分,如果长度为1,那么dp[i] nums[i]; 如果长度大于1,那么当前位置的最大和就为 i-1 位置最大和 …...
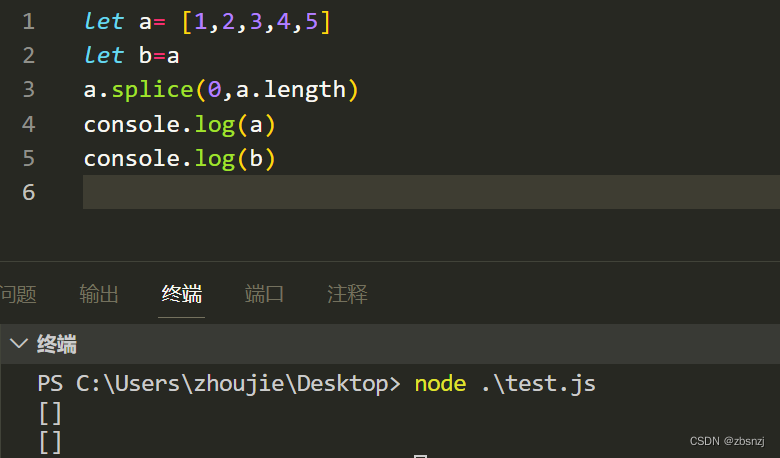
js 清空数组的方法
1、直接赋值空数组 let array [1, 2, 3, 4, 5]; array []; 这种方法并不推荐,如下图所示: 虽然a数组确实变为了空数组,但这种方法只是修改了a的指向,把a指向一个新的空数组,然而[1,2,3,4,5]这个数组并没有被清除&a…...
QT中使用QProcess执行命令,实时获取数据,例如进度条
前言 因为之前写了一个接收和发送文件的脚本,然后又需要获取进度,同步到进度条中。 效果: 使用正则匹配,获取命令行命令中的以下数据,然后同步到进度条 源码demo: 非完整代码: #include <Q…...
绘图设计:用Draw.io绘制图形技巧大全(含统一建模语言UML模板)
一、常见UML模板 1.流程图 2.用例图 include是包含关系,extend是扩展关系 简而言之,include是子集指向父集;而extend是扩展用例指向基础用例(基础用例可以理解为系统核心功能,扩展用例是可选的,不是必须…...

被唤醒的“第二十条”深入人心
近来张艺谋执导的电影《第二十条》,因为它与正在召开中的全国两会所发布的《最高人民法院工作报告》联系相当紧密,加之可免费收看,网民便相互转告,于是此信息条目立即冲上了网络热搜榜,观者如潮。因为最高人民法院工作…...
信息泄漏原理以及修复方法)
PHPInfo()信息泄漏原理以及修复方法
漏洞名称:PHPInfo信息泄漏、phpinfo()函数信息泄漏 漏洞描述: phpinfo()函数返回的信息中包含了服务器的配置信息,包括: 1)PHP编译选项以及文件扩展名的相关信息; 2)php的版本信息 3&#…...

202441读书笔记|《笠翁对韵》—— 金菡萏,玉芙蓉,酒晕微酡琼杏颊,香尘浅印玉莲双
202441读书笔记|《笠翁对韵》——金菡萏,玉芙蓉,酒晕微酡琼杏颊,香尘浅印玉莲双 《作家榜名著:笠翁对韵》作者李渔,霍俊明。是所有词句都有注音的一本书,轻松学不认识的字,非常朗朗上口的对偶词…...

006-v-model原理
v-model原理 简介v-model应用在输入框上v-model应用在组件上 简介 由 属性绑定(v-bind:value“searchText”) 配合 input事件监听(v-on:input“searchText event.target.value”) 实现。 应用在组件上由 props: {value: xxx } ,this.$emit(‘input’, xxx ) 完成。…...

Ubuntu下使用DAPLink(OpenOCD)
目录 1. 下载OpenOCD源代码 2. 编译代码 2.1 运行bootstrap 2.2 安装关联库 2.3 运行./configure 2.4 运行make 2.5 运行sudo make install 3. 烧录程序 3.1 挂起MCU 3.2 写入镜像 3.3 校验镜像 通过OpenOCD实现,在Ubuntu18 64bit下验证。 1. 下载OpenOC…...
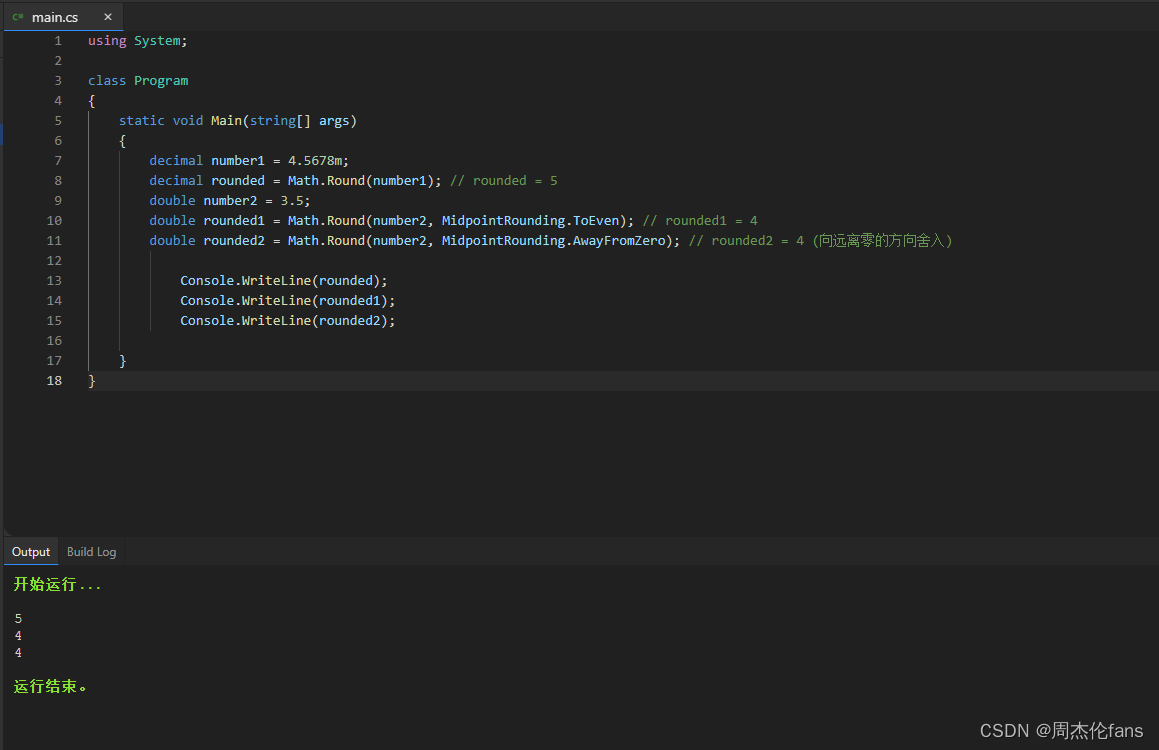
C# 中 Math.Round 数学函数
在 C# 中,Math.Round 是一个数学函数,用于对一个浮点数进行四舍五入操作。它接受一个浮点数作为输入,并返回一个最接近输入值的整数或指定小数位数的浮点数。 Math.Round 方法有多个重载,其中最常用的重载有以下两种形式…...

力扣---接雨水---单调队列
题目: 单调队列思想: 没有思路的小伙伴可以先把这个想清楚哦:力扣hot10---大根堆双端队列-CSDN博客 从上面的图就可以发现,如果柱子呈递减序列,那么不会接到雨水,只要有一个小凸起柱子,那么这个…...

微分学<4>——微分中值定理
索引 微分中值定理极值定义4.1 极大(小)值定理4.1 Fermat引理定理4.2 Rolle定理 Lagrange中值定理定理4.3 Lagrange中值定理定理4.4 Cauchy中值定理 导数对函数性质的刻画Jensen不等式 微分中值定理 极值 定义4.1 极大(小)值 若存在 x 0 x_{0} x0的邻域 U ( x 0 , δ ) U\…...
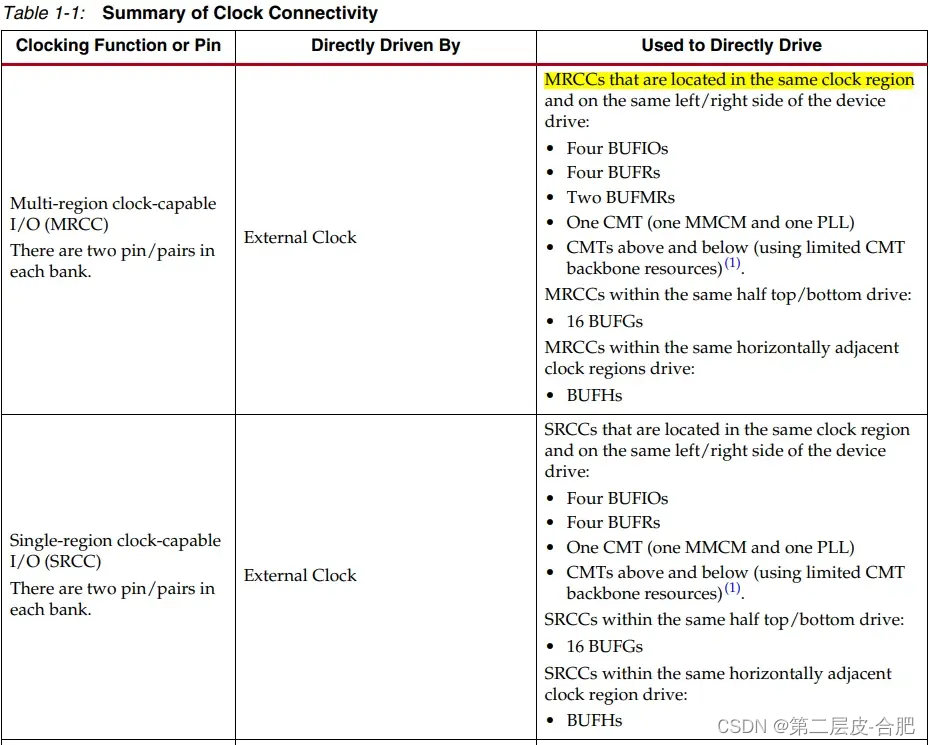
FPGA的时钟资源
目录 简介 Clock Region详解 MRCC和SRCC的区别 BUFGs 时钟资源总结 简介 7系列FPGA的时钟结构图: Clock Region:时钟区域,下图中有6个时钟区域,用不同的颜色加以区分出来 Clock Backbone:从名字也能看出来&#x…...

LeetCode27: 移除元素
题目描述 给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。 不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。 元素的顺序可以改变。你不需要考虑数组中超出…...

Python使用Beautiful Soup及解析html获取元素并提取内容值
Python使用Beautiful Soup及解析html获取元素并提取内容值 1. 包括解析获取标题2. 根据标签及id获取所有元素3. 根据标签及class获取所有元素4. 获取元素下的标签的值5. 获取元素下的parent及child的元素的值参考 1. 包括解析获取标题 2. 根据标签及id获取所有元素 3. 根据标…...

如何清除keep-alive缓存
在 Vue.js 中,使用 <keep-alive> 组件可以将组件保留在内存中,以避免重复渲染和销毁,从而提高性能。如果需要手动清除 <keep-alive> 组件的缓存,可以通过两种方法来实现: 通过 $destroy 方法销毁组件&…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

Windows电脑能装鸿蒙吗_Windows电脑体验鸿蒙电脑操作系统教程
鸿蒙电脑版操作系统来了,很多小伙伴想体验鸿蒙电脑版操作系统,可惜,鸿蒙系统并不支持你正在使用的传统的电脑来安装。不过可以通过可以使用华为官方提供的虚拟机,来体验大家心心念念的鸿蒙系统啦!注意:虚拟…...

Yii2项目自动向GitLab上报Bug
Yii2 项目自动上报Bug 原理 yii2在程序报错时, 会执行指定action, 通过重写ErrorAction, 实现Bug自动提交至GitLab的issue 步骤 配置SiteController中的actions方法 public function actions(){return [error > [class > app\helpers\web\ErrorAction,],];}重写Error…...
