代码详解:2024美团春招实习笔试第一场0309,是难还是简单?
前言:
1.第一题(模拟)
2.第二题(模拟)
3.第三题(二维前缀和)
4.第四题的思维(双指针)
5.第五题难度比较大(并查集+删边+离散化)
一.小美的MT
MT 是美团的缩写,因此小美很喜欢这两个字母。
现在小美拿到了一个仅由大写字母组成字符串,她可以最多操作k次,每次可以修改任意一个字符。小美想知道,操作结束后最多共有多少个'M'和'T'字符?
输入描述
第一行输入两个正整数n,k,代表字符串长度和操作次数。第二行输入一个长度为n的、仅由大写字母组成的字符串。1<=k<=n<=10^5
输出描述
输出操作结束后最多共有多少个'M'和'T'字符。
示例 1
输入
5 2
MTUAN输出
4说明
修改第三个和第五个字符,形成的字符串为 MTTAM,这样共有 4 个'M'和'T'。
思路与代码
1.首先统计字符串中除了M和T以外的字符的个数,记为add。
2.操作次数为k,因此最多可以min(k,add)将个字符变为M和T
3.再加上之前的M和T字符的个数。
4.结果为n-add+min(k,add);
C++:
#include <bits/stdc++.h>
using namespace std;
int main() {int n, k, sum = 0;cin >> n >> k;string s;cin >> s;int add = 0;for (int i = 0; i < s.size(); i++) {if (s[i] != 'M' && s[i] != 'T') {add++;}}sum = n - add + min(k, add);cout << sum << "\n";return 0;
}
Java:
import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n, k, sum = 0;n = scanner.nextInt();k = scanner.nextInt();String s = scanner.next();int add = 0;for (int i = 0; i < s.length(); i++) {if (s.charAt(i) != 'M' && s.charAt(i) != 'T') {add++;}}sum = n - add + Math.min(k, add);System.out.println(sum);}
}
二.小美的数组询问
小美拿到了一个由正整数组成的数组,但其中有一些元素是未知的(用 0 来表示)。
现在小美想知道,如果那些未知的元素在区间[l,r]范围内随机取值的话,数组所有元素之和的最小值和最大值分别是多少?
共有q次询问。
输入描述
第一行输入两个正整数n,q,代表数组大小和询问次数。
第二行输入n个整数ai,其中如果输入ai的为 0,那么说明ai是未知的。
接下来的q行,每行输入两个正整数l,r,代表一次询问。
1<=n,q<=10^5
0<=ai<=10^9
1<=l<=r<=10^9输出描述
输出q行,每行输出两个正整数,代表所有元素之和的最小值和最大值。
示例 1
输入
3 2
1 0 3
1 2
4 4输出
5 6
8 8说明
只有第二个元素是未知的。
第一次询问,数组最小的和是 1+1=3=5,最大的和是 1+2+3=6。
第二次询问,显然数组的元素和必然为 8。思路与代码
1.循环一遍,sum记录非0的情况下的和,res统计0的数量。
2.最小值就是0的数量 * 区间左值(res*l),反之最大值就是0的数量*区间右值(res*r)。
3.答案就是最小:sum+res*l,最大:sum+res*r;
C++
#include <bits/stdc++.h>
using namespace std;int main() {int n, q;cin >> n >> q;vector<int> a(n);for (int i = 0; i < n; i++) {cin >> a[i];}int res = 0;int sum = 0;for (int i = 0; i < n; i++) {if (a[i] == 0) {res++;}sum += a[i];}for (int i = 0; i < q; i++) {int l, r;cin >> l >> r;cout << sum + res *l << " " << sum + res *r << endl;}return 0;
}
Java
import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt();int q = sc.nextInt();int[] a = new int[n];for (int i = 0; i < n; i++) {a[i] = sc.nextInt();}int res = 0;int sum = 0;for (int i = 0; i < n; i++) {if (a[i] == 0) {res++;}sum += a[i];}for (int i = 0; i < q; i++) {int l = sc.nextInt();int r = sc.nextInt();System.out.println((sum + res * l) + " " + (sum + res * r));}}
}
三.小美的平衡矩阵
小美拿到了一个n*n 的矩阵,其中每个元素是 0 或者 1。
小美认为一个矩形区域是完美的,当且仅当该区域内 0 的数量恰好等于 1 的数量。
现在,小美希望你回答有多少个i*i的完美矩形区域。你需要回答1<=i<=n的所有答案。
输入描述
第一行输入一个正整数n,代表矩阵大小。
接下来的n行,每行输入一个长度为n的01 串,用来表示矩阵。
输出描述
输出n行,第i行输出的i*i完美矩形区域的数量。
示例 1
输入
4
1010
0101
1100
0011输出
0
7
0
1思路与代码
二维前缀和。n<=200.所以可以n^3进行解决题目
1.枚举所有的边长i的正方形.
2.如果0和1的数量各一半,那么就是判断正方形的和是否为i*i / 2,如果是就++。
3.计算时:
第一层循环枚举矩形长度i,
第二,三层循环分别枚举矩形的左上角的端点(x,y)
对应右下角的端点则为(x+i-1,y+i-1)
C++:
#include <bits/stdc++.h>
using namespace std;
const int N = 510;
int n;
char a[N][N];
int s[N][N];
int main() {cin >> n;for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {cin >> a[i][j];}}for (int i = 1; i <= n; i ++ )for (int j = 1; j <= n; j ++ )s[i][j] = s[i][j - 1] + s[i - 1][j] - s[i - 1][j - 1] + (a[i][j] == '1');for (int i = 1; i <= n; i++) {int cnt = 0;for (int x = 1; x <= n - i + 1; x++) {for (int y = 1; y <= n - i + 1; y++) {int sum = s[x + i - 1][y + i - 1] - s[x + i - 1][y - 1] - s[x - 1][y + i - 1] + s[x - 1][y - 1];if (sum * 2 == i * i) {cnt++;}}}cout << cnt << endl;}return 0;
}Java:
import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int N = 510;int n = scanner.nextInt();char[][] a = new char[N][N];int[][] s = new int[N][N];for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {a[i][j] = scanner.next().charAt(0);}}for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {s[i][j] = s[i][j - 1] + s[i - 1][j] - s[i - 1][j - 1] + (a[i][j] == '1' ? 1 : 0);}}for (int i = 1; i <= n; i++) {int cnt = 0;for (int x = 1; x <= n - i + 1; x++) {for (int y = 1; y <= n - i + 1; y++) {int sum = s[x + i - 1][y + i - 1] - s[x + i - 1][y - 1] - s[x - 1][y + i - 1] + s[x - 1][y - 1];if (sum * 2 == i * i) {cnt++;}}}System.out.println(cnt);}}
}
四.小美的区间删除
小美拿到了一个大小为n的数组,她希望删除一个区间后,使得剩余所有元素的乘积末尾至少有k个 0。小美想知道,一共有多少种不同的删除方案?
输入描述
第一行输入两个正整数n,k。第二行输入n个正整数ai,代表小美拿到的数组。
1<=n,k<=10^5
1<=ai<=10^9输出描述
一个整数,代表删除的方案数。
示例 1
输入
5 2
2 5 3 4 20输出
4说明
第一个方案,删除[3]。
第二个方案,删除[4]。
第三个方案,删除[3,4]。
第四个方案,删除[2]。思路与代码
2和5的因子个数。2*5=10;2^i*5^j == min(i,j)==0的数量 2*5=10
使用双指针
区间的一个长度越大,那么末尾0的个数越多,单调性,
使用双指针
1.我们首先统计整个数组的2和5的因子3数量,和每个元素对应的5的因子数量。
2.维护2个指针l,r
3.如果l,r的区间min(cnt2,cnt5)>=k,我们答案就累加l-r+1;
C++:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
int a2[N], a5[N];
int cnt2 = 0, cnt5 = 0;
int n, k, x;void cnt2_cnt5_count() {for (int i = 0; i < n; i ++) {cin >> x;while (x % 2 == 0) {a2[i] ++;x /= 2;cnt2 ++;}while (x % 5 == 0) {a5[i] ++;x /= 5;cnt5 ++;}}
}int main() {cin >> n >> k;cnt2_cnt5_count();int l = 0;long long res = 0;for (int r = 0; r < n; r ++) {cnt2 -= a2[r];cnt5 -= a5[r];while (min(cnt2, cnt5) < k && l <= r) {cnt2 += a2[l];cnt5 += a5[l];l ++;}res += (long long)(r - l + 1);}cout << res << endl;return 0;
}Java:
import java.util.Scanner;public class Main {static final int N = 1000010;static int[] a2 = new int[N];static int[] a5 = new int[N];static int cnt2 = 0, cnt5 = 0;static int n, k, x;public static void cnt2Cnt5Count() {Scanner input = new Scanner(System.in);for (int i = 0; i < n; i++) {x = input.nextInt();while (x % 2 == 0) {a2[i]++;x /= 2;cnt2++;}while (x % 5 == 0) {a5[i]++;x /= 5;cnt5++;}}}public static void main(String[] args) {Scanner input = new Scanner(System.in);n = input.nextInt();k = input.nextInt();cnt2Cnt5Count();int l = 0;long res = 0;for (int r = 0; r < n; r++) {cnt2 -= a2[r];cnt5 -= a5[r];while (Math.min(cnt2, cnt5) < k && l <= r) {cnt2 += a2[l];cnt5 += a5[l];l++;}res += (long) (r - l + 1);}System.out.println(res);}
}五.小美的朋友关系
小美认为,在人际交往中,但是随着时间的流逝,朋友的关系也是会慢慢变淡的,最终朋友关系就淡忘了。
现在初始有一些朋友关系,存在一些事件会导致两个人淡忘了他们的朋友关系。小美想知道某一时刻中,某两人是否可以通过朋友介绍互相认识?
事件共有 2 种:
1 u v:代表编号 u 的人和编号 v 的人淡忘了他们的朋友关系。
2 u v:代表小美查询编号 u 的人和编号 v 的人是否能通过朋友介绍互相认识。
注:介绍可以有多层,比如 2 号把 1 号介绍给 3 号,然后 3 号再把 1 号介绍给 4 号,这样 1 号和 4 号就认识了。
输入描述
第一行输入三个正整数n,m,q,代表总人数,初始的朋友关系数量,发生的事件数量。接下来的m行,每行输入两个正整数u,v,代表初始编号u的人和编号v的人是朋友关系。接下来的q行,每行输入三个正整数op,u,v,含义如题目描述所述。
1<=n <= 10^9
1<= m,q<= 10^5
1<= u,v<= n
1<= op <= 2
保证至少存在一次查询操作。输出描述
对于每次 2 号操作,输出一行字符串代表查询的答案。如果编号 u 的人和编号 v 的人能通过朋友介绍互相认识,则输出"Yes"。否则输出"No"。
示例 1
输入
5 3 5
1 2
2 3
4 5
1 1 5
2 1 3
2 1 4
1 1 2
2 1 3输出
Yes
No
No说明
第一次事件,1 号和 5 号本来就不是朋友,所以无事发生。
第二次事件是询问,1 号和 3 号可以通过 2 号的介绍认识。
第三次事件是询问,显然 1 号和 4 号无法互相认识。
第四次事件,1 号和 2 号淡忘了。
第五次事件,此时 1 号无法再经过 2 号和 3 号互相认识了。
思路与代码
离线处理数据(map)+并查集+逆向思维。
1.离线处理,因为这里的n非常大1e9,后面是使用并查集构造n个节点,father数组肯定装不下.
2.并查集处理加边,删边转换下思路
3.如果我们已经找出所有可能要删除的边,然后假设所有边都删除了,构建一个最终的并查集(这个并查集并不影响后面的删边的情况)。
4.逆向遍历所有的q次操作,如果是查询(1操作),使用并查集直接查出即可;如果是删除(2操作),则往并查集添加边。
C++:
#include <bits/stdc++.h>
using namespace std;unordered_map<int, int> father;
int find(int x) {return father[x] == x ? x : (father[x] = find(father[x]));
}void merge(int x, int y) {int i = find(x), j = find(y);if (i != j)father[i] = j;
}struct node {int op;int u;int v;
};int main() {int n, m, p;cin >> n >> m >> p;vector<node> all(p);set<pair<int, int> > q;set<pair<int, int> > q_del;for (int i = 0; i < m; i ++) {int u, v;cin >> u >> v;father[u] = u;father[v] = v;q.insert({u, v});//初始化需要建立的边}for (int i = 0; i < p; i ++) {cin >> all[i].op >> all[i].u >> all[i].v;father[all[i].u] = all[i].u;father[all[i].v] = all[i].v;if (all[i].op == 1) {q_del.insert({all[i].u, all[i].v});//需要删除的边}}for (auto e : q_del) {int u = e.first, v = e.second;if (q.count({u, v}) || q.count({v, u})) {q.erase(e);}}for (auto e : q) {merge(e.first, e.second);}vector<string> res;for (int i = p - 1; i >= 0; i --) {if (all[i].op == 1) {merge(all[i].u, all[i].v);} else {if (find(all[i].u) == find(all[i].v)) {res.push_back("Yes");} else {res.push_back("No");}}}reverse(res.begin(), res.end());for (string s : res) {cout << s << endl;}return 0;
}Java:
import java.util.*;class Main {static Map<Integer, Integer> father;public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int m = scanner.nextInt();int p = scanner.nextInt();father = new HashMap<>();List<Node> all = new ArrayList<>();Set<Pair> q = new HashSet<>();Set<Pair> q_del = new HashSet<>();for (int i = 0; i < m; i++) {int u = scanner.nextInt();int v = scanner.nextInt();father.put(u, u);father.put(v, v);q.add(new Pair(u, v)); // 初始化需要建立的边}for (int i = 0; i < p; i++) {int op = scanner.nextInt();int u = scanner.nextInt();int v = scanner.nextInt();all.add(new Node(op, u, v));father.put(u, u);father.put(v, v);if (op == 1) {q_del.add(new Pair(u, v)); // 需要删除的边}}for (Pair e : q_del) {int u = e.first, v = e.second;if (q.contains(new Pair(u, v)) || q.contains(new Pair(v, u))) {q.remove(e);}}for (Pair e : q) {merge(e.first, e.second);}List<String> res = new ArrayList<>();for (int i = p - 1; i >= 0; i--) {if (all.get(i).op == 1) {merge(all.get(i).u, all.get(i).v);} else {if (find(all.get(i).u) == find(all.get(i).v)) {res.add("Yes");} else {res.add("No");}}}Collections.reverse(res);for (String s : res) {System.out.println(s);}}static int find(int x) {return father.get(x) == x ? x : find(father.get(x));}static void merge(int x, int y) {int i = find(x);int j = find(y);if (i != j) {father.put(i, j);}}static class Node {int op;int u;int v;Node(int op, int u, int v) {this.op = op;this.u = u;this.v = v;}}static class Pair {int first;int second;Pair(int first, int second) {this.first = first;this.second = second;}@Overridepublic boolean equals(Object obj) {if (this == obj) {return true;}if (obj == null || getClass() != obj.getClass()) {return false;}Pair pair = (Pair) obj;return first == pair.first && second == pair.second;}@Overridepublic int hashCode() {return Objects.hash(first, second);}}
}
最后:
觉得讲解不错的可以关注,反响不错的话,会更新此系列讲解视频,最后的最后祝大家offer满满!!!
相关文章:

代码详解:2024美团春招实习笔试第一场0309,是难还是简单?
前言: 1.第一题(模拟) 2.第二题(模拟) 3.第三题(二维前缀和) 4.第四题的思维(双指针) 5.第五题难度比较大(并查集删边离散化) 一.小美的MT MT 是美团的…...
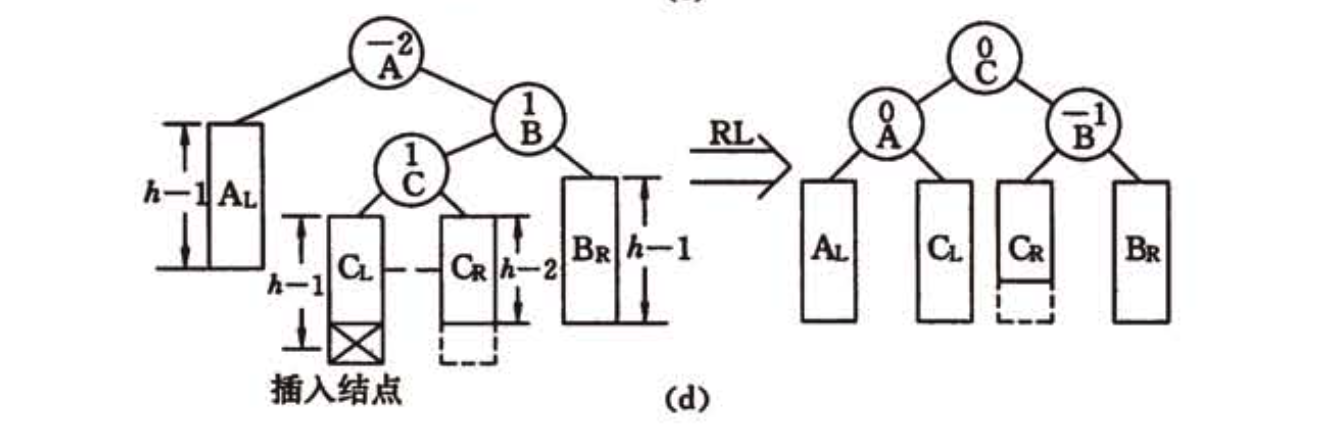
平衡二叉树
前言 在关键字排列随机的情况下,二叉排序树的平均查找长度和 l o g n log n logn是等数量级的。在某些情况下,尚需在构成二叉排序树的过程中进行“平衡化”处理,使其成为平衡二叉树。 如果任何初始化序列构成的二叉排序树都是平衡二叉树&…...

脚本自动化 设置快捷方式并设置为管理员运行
自动化创建快捷方式并设置为始终以管理员权限运行,可以通过编写批处理脚本来实现。以下是一个创建.bat批处理文件快捷方式并设置为管理员运行的示例脚本: batch echo off set SCRIPT_PATH"C:\Scripts\myScript.bat" set SHORTCUT_PATH"%…...

TypeScript学习笔记(上):TypeScript的介绍、安装及常用类型
我对TypeScript的理解就是,TypeScript是增加了类型校验的JavaScript,能够把运行期错误提升至编译期 目录 TypeScript是什么? 安装编译 TS 的工具包 运行 TS 的步骤 TypeScript 常用类型 JS 已有类型 TS 新增类型 简单数据类型 数组类…...

Vue3学习记录(六)--- 组合式API之依赖注入和异步组件
一、依赖注入 1、简介 在前面的笔记中,我们学习过父组件向子组件传递数据时,需要借助props来实现。但如果父组件想要向孙子组件传递数据,那就要连续使用两层props逐级向下传递,如果要接收数据的是更深层的后代组件࿰…...
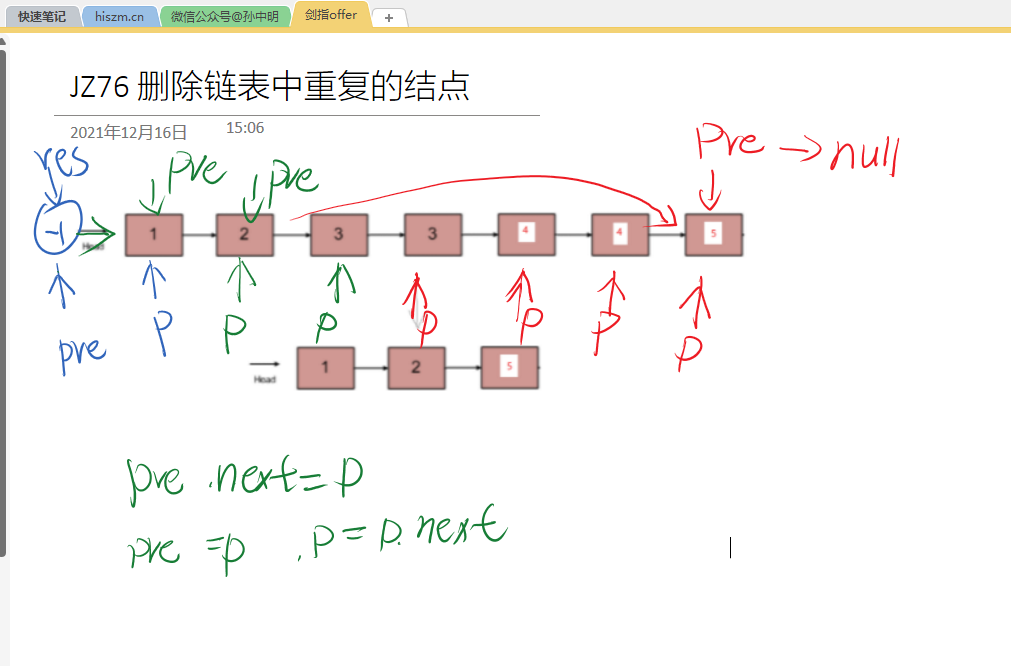
JZ76 删除链表中重复的结点
/*public class ListNode {int val;ListNode next null;ListNode(int val) {this.val val;} } */import java.util.*; public class Solution {public ListNode deleteDuplication(ListNode pHead) {//初步想想法: 弄一个hashmap 然后进行key存储起来。然后 如果存…...

20.2 nginx
20.2 nginx 1. 学习目标2. 介绍2.1 正向代理2.2 反向代理2.3 动态静态资源分离2.4 nginx优缺点3. 安装3.1 Linux安装****************************************************************************************************************************************************…...

MySQL学习Day26——事务基础知识
一、数据库事务概述: 事务是数据库区别于文件系统的重要特性之一,事务会让数据始终保持一致性,能通过事务机制恢复到某个时间点,可以保证提交到数据库的修改不会因为系统崩溃而丢失 1.查看引擎支持事务的情况:只有InnoDB存储引擎支持事务 SHOW ENGINES; 2.基本概念: 事…...
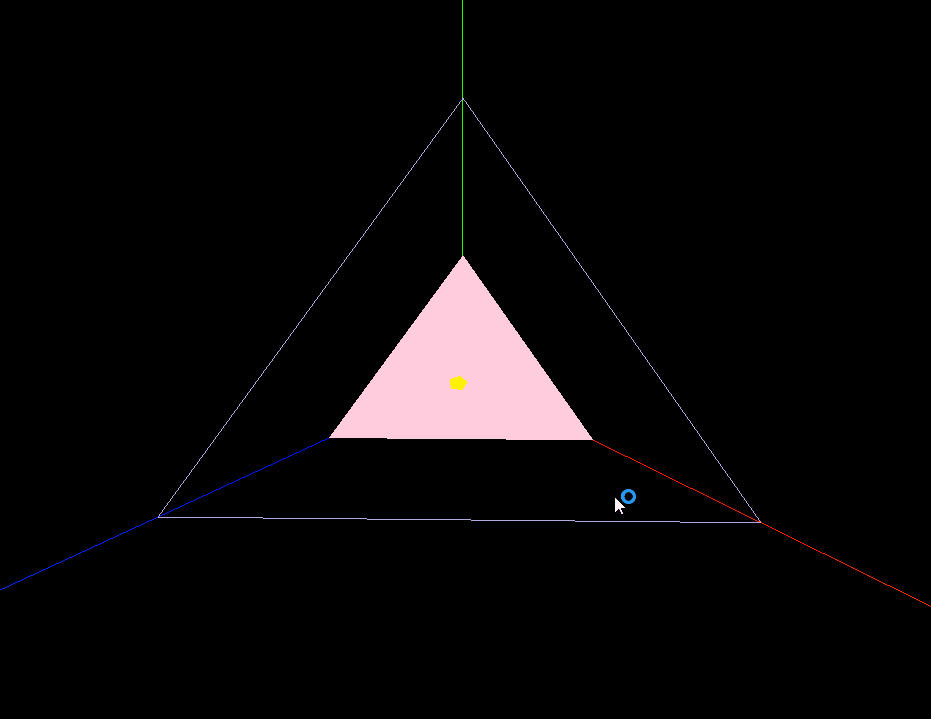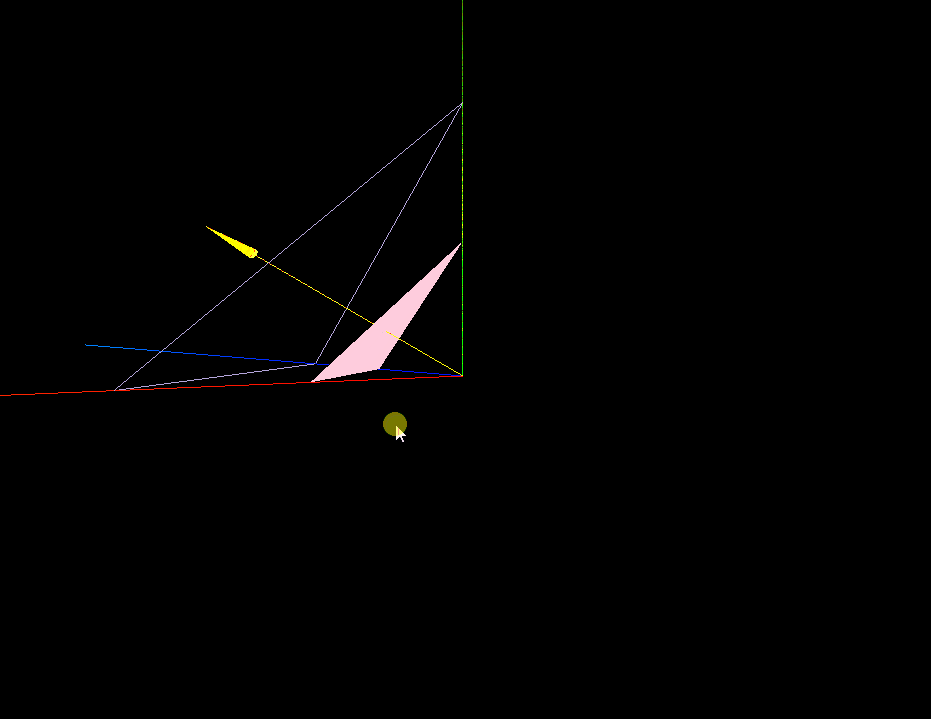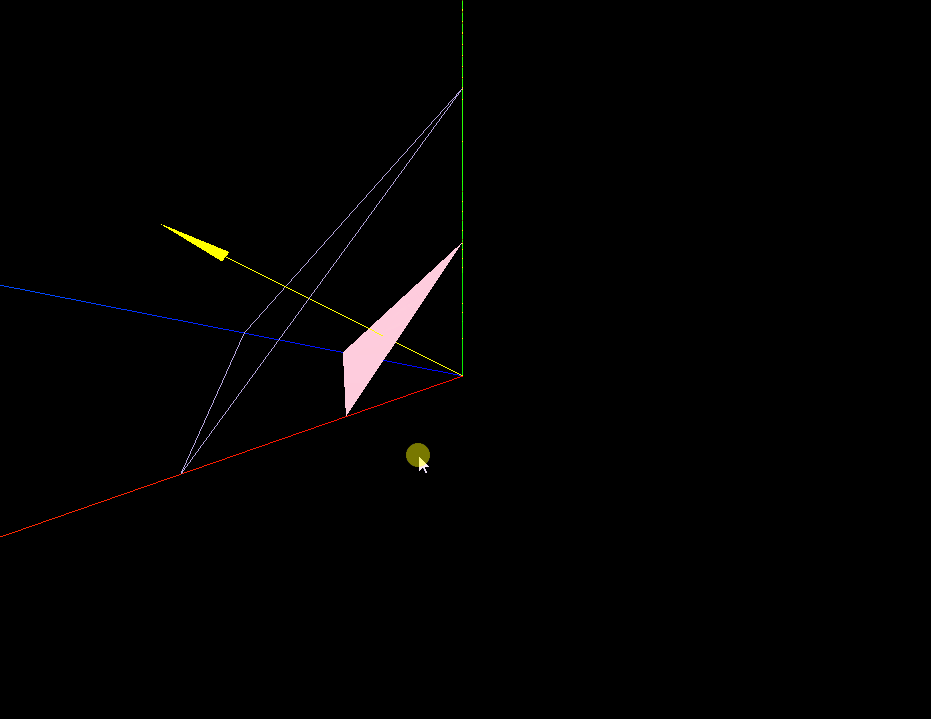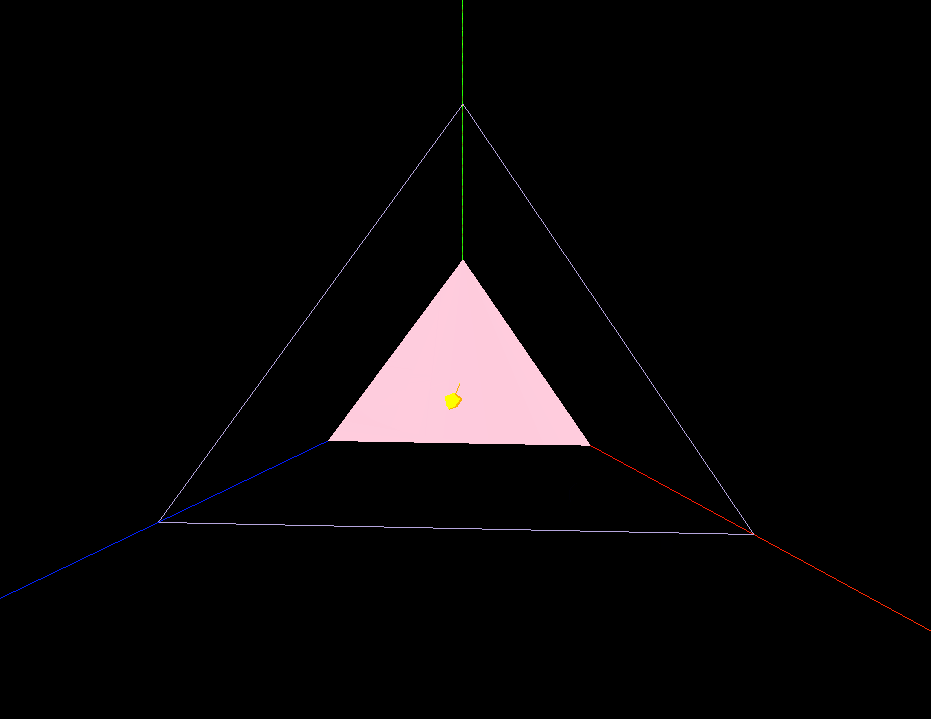
three.js 射线Ray,三维空间中绘制线框
效果: 代码: <template><div><el-container><el-main><div class"box-card-left"><div id"threejs"></div> <div>{{ res1 }}</div> <div>{{ res2 }}</div><…...

【Demo】游戏小地图
简介 该Demo基于2D关卡随机生成项目进行实现,旨在初步探索游戏小地图的制作。 演示 MiniMapDemo 资源下载 百度网盘(提取码:1314) 如果这篇文章对你有帮助,请给作者点个赞吧!...
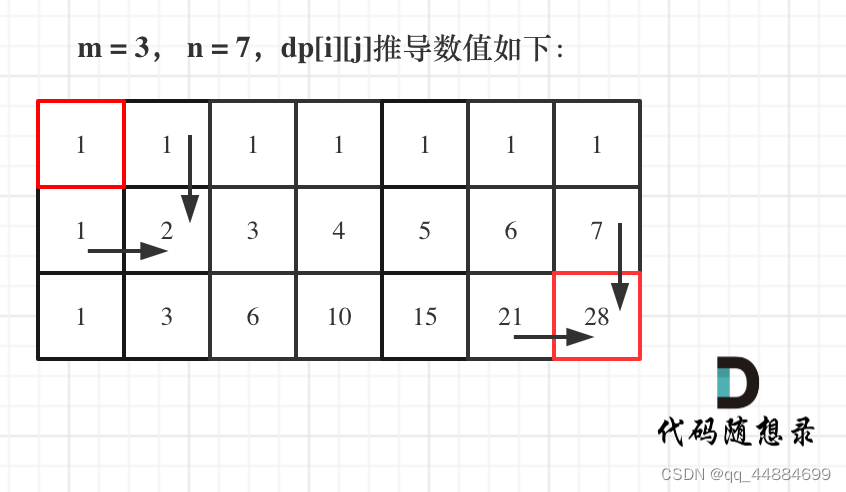
代码随想录算法训练营Day39 || leetCode 762.不同路径 || 63. 不同路径 II
62.不同路径 每一位的结果等于上方与左侧结果和 class Solution { public:int uniquePaths(int m, int n) {vector<vector<int>> dp(m,vector(n,0));for (int i 0; i < m; i) dp[i][0] 1;for (int j 0; j < n; j) dp[0][j] 1;for (int i 1; i < m; …...
函数的使用)
Qt中parent()函数的使用
情景(需求)抽象: A类对象是B类对象的成员变量。 B类对象是A类对象的父亲。 A类对象中包含按钮,点击按钮,调用B类的成员函数。 示例: A类: #pragma once#include <QWidget> #include "ui_QtWidgetsCla…...
流程控制)
Python基础学习(5)流程控制
文章目录 一. 程序三大执行流程二. 分支结构1.单分支结构(if)2.双分支结构(if..else)3.多分支结构(if..elif..else) 二,缩进(tab键)三,循环结构1.while循环2.for循环①遍历字典 五.break,continue和pass语句1.break,continue2.pass Python基础学习(1)基本…...
代码随想录刷题笔记 DAY 42 | 最后一块石头的重量 II No.1049 | 目标和 No.494 | 一和零 No.474
文章目录 Day 4301. 最后一块石头的重量 II(No. 1049)<1> 题目<2> 笔记<3> 代码 02. 目标和(No. 494)<1> 题目<2> 笔记<3> 代码 03. 一和零(No. 474)<1> 题目&l…...
)
793.高精度乘法(acwing)
文章目录 793.高精度乘法题目描述高精度乘法 793.高精度乘法 题目描述 给定两个正整数A和B,请你计算A * B的值。 输入格式 共两行,第一行包含整数A,第二行包含整数B。 输出格式 共一行,包含A * B的值。 数据范围 1≤A的长度≤…...

考研经验|如何从考研失败中走出来?
对我来说,太丢人了 其实我在本科的时候在同学眼中,一直很优秀,每年奖学金必有我的,国家励志奖学金,国家奖学金,这种非常难拿的奖学金,我也拿过,本科期间学校有一个公费去新西兰留学的…...

SpringBoot如何修改pom依赖的默认版本号
1、找到SpringBoot父工程依赖。 <parent><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-parent</artifactId><version>2.3.5.RELEASE</version> </parent>2、ctrl 鼠标左键点击<artifact…...

UDP与TCP:了解这两种网络协议的不同之处
🤍 前端开发工程师、技术日更博主、已过CET6 🍨 阿珊和她的猫_CSDN博客专家、23年度博客之星前端领域TOP1 🕠 牛客高级专题作者、打造专栏《前端面试必备》 、《2024面试高频手撕题》 🍚 蓝桥云课签约作者、上架课程《Vue.js 和 E…...

String、StringBuffer基本用法
一、StringBuffer基本用法 1.append():字符串连接操作 StringBuffer sb new StringBuffer();sb.append("a");sb.append("b");sb.append("c");sb.append("哈哈").append("d");System.out.println(sb);2.insert():在任意位…...

蓝桥杯刷题5--GCD和LCM
目录 1. GCD 1.1 性质 1.2 代码实现 2. LCM 2.1 代码实现 3. 习题 3.1 等差数列 3.2 Hankson的趣味题 3.3 最大比例 3.4 GCD 1. GCD 整数a和b的最大公约数是能同时整除a和b的最大整数,记为gcd(a, b) 1.1 性质 GCD有关的题目一般会考核GCD的性质。 …...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...
