【数据结构初阶 9】内排序
文章目录
- 🌈 1. 直接插入排序
- 🌈 2. 希尔排序
- 🌈 3. 简单选择排序
- 🌈 4. 堆排序
- 🌈 5. 冒泡排序
- 🌈 6. 快速排序
- 6.1 霍尔版快排
- 6.2 挖坑版快排
- 6.3 双指针快排
- 6.4 非递归快排
- 🌈 7. 归并排序
- 7.1 递归版归并
- 7.2 迭代版归并
- 🌈 8. 计数排序
🌈 1. 直接插入排序
基本思想
- 将一组数据分成两个部分:已有序数据 + 待排序数据
- 每步将一个待排序的数据,按值的大小插入到已有序数据的适当位置上,直到全部有序为止。
- 即:边插入边排序,保证已有序数据这部分随时都是有序的。
实现步骤
- 在一串未排序的数据中,第一个数肯定有序,必须从第一个数开始进行插入排序。
- 取出待排序部分的第一个元素 key,在已排序数据部分从后往前扫描。
- 在已有序部分的数据如果 > key,则将该元素往后挪一位。
- 重复执行步骤 3,直到在已有序部分找到第一个 <= key 的元素,将 key 插入其后。
- 如果已排序部分的值全部 < key,则 key 插入到第一个位置,如果全部 > key 则 key 的位置不用动相当于直接插入到已有序数据的最后。
- 重复执行步骤 2 ~ 5。
代码实现
// 直接插入排序
void insert_sort(int data[], int n)
{ // 整体排序for (int i = 0; i < n - 1; i++) // 最后要插入的值为第 n 个,i 必须小于 n - 1{int end = i; // 设 [0,end] 为有序区间,将 end + 1 插入该区间 int key = data[end + 1]; // 先保存待插入的值,防止在往后挪动过程中将其覆盖// 单趟排序while (end >= 0) // 在有序区间从后往前扫描{if (key < data[end]) // 将所有 > key 的数都往后挪{data[end + 1] = data[end];end--;}else{break; // 在 end 处出现了第一个 <= key 的数}}data[end + 1] = key; // 将 key 插入有序区间有两种情况:// 1. 区间内的值都 > key,此时 end 等于 -1,将 key 插入到第一个位置// 2. 将 key 插入到第一个出现 <= key 的数的后面}
}
特性总结
- 时间复杂度:最坏的情况逆序有序时 O(N2);最好的情况顺序有序时 O(N)
- 空间复杂度:O(1)
- 稳定性:不稳定排序
🌈 2. 希尔排序
基本思想
- 先将整个待排序数据序列分隔成若干个子序列分别进行直接插入排序
- 待整个序列中的数据基本有序时,再对全体数据进行直接插入排序。
实现步骤
- 选一个小于待排序数据个数 n 的整数 gap 作为间隔,然后将间隔为 gap 的元素分在同一组。
- 例如:假设 gap 为 2,则下标为 0 2 4 6 的元素为一组,下标为 1 3 5 7 的元素为一组。
- 对每一组的元素进行直接插入排序,然后再将间隔 gap 缩小。
- 重复上述操作直到间隔 gap 缩小到 1 时,等于将所有数据划分为一组,此时所有数据最接近有序,直接对整组数据进行直接插入排序即可。
代码实现
- 如果使用 gap / 2 的方式缩短间隔速度太慢,使用 gap / 3 + 1 缩小间隔 既能快速缩短间隔,也能保证最后能缩短为 1 间隔。
// 希尔排序
void shell_sort(int data[], int n)
{int gap = n; while (gap > 1) // gap > 1 时是预排序,= 1 时是直接插入排序{gap = gap / 3 + 1; // 快速缩小间隔,且保证最后变为 1 间隔for (int i = 0; i < n - gap; i += gap) // 对 gap 分隔的每一组都进行直接插入排序{int end = i; // end 记录每一组的第一个元素int key = data[end + gap]; // 同一组内 end 后待插入的值与其隔了 gap 个数while (end >= 0) // 组内单趟排序{ if (key < data[end]) // 将组内所有 > key 的数都后移{ data[end + gap] = data[end];end -= gap;}else{break; // 在组内 end 处出现了第一个 <= key 的数}}data[end + gap] = key; // 将 key 插入有序区间}}
}
特性总结
- 时间复杂度:约等于 O(N1.3)
- 空间复杂度:O(1)
- 稳定性:不稳定排序
🌈 3. 简单选择排序
基本思想
- 每一趟都从待排序的数据中选出 最大 / 最小 值放在其最终的位置,然后待排序数据个数 - 1。
- 重复执行上述操作,直到待排序数据个数为 0 即可。
代码实现
- 每一趟排序可以直接选出待排序数据的 最大和最小 值放在他们最终的的位置,最大放最右边,最小放最左边。这种情况下待排序数据的区间会从两边往中间收缩,直到区间两端相等为止。
// 选择排序
void select_sort(int data[], int n)
{int i = 0;int begin = 0; // 记录待排序区间的左端下标int end = n - 1; // 记录待排序区间的右端下标while (begin < end) // [begin, end] 相等时没有待排序区间了{int mini = begin; // 记录待排序数据的最小数据下标int maxi = end; // 记录待排序数据的最大数据下标for (i = begin + 1; i <= end; i++) // 每一趟都找出待排序数据的最大和最小值下标{if (data[mini] > data[i]) // 如果出现了比当前最小值还小的值{mini = i; // 更新最小值的下标}if (data[maxi] < data[i]) // 如果出现了比当前最大值还大的值{maxi = i; // 更新最大值的下标}}Swap(&data[begin], &data[mini]); // 将最小值放到待排序数据的最左边if (maxi == begin) // 如果第一个数就是最大值{maxi = mini; // 在前面的交换后,最大值的下标就跑到 mini}Swap(&data[end], &data[maxi]); // 将最大值放到待排序数据的最右边begin++; // 往中间缩小待排序区间end--;}
}
特性总结
- 时间复杂度:最坏情况 O(N2),最好情况 O(N2)
- 空间复杂度:O(1)
- 稳定性:稳定排序
🌈 4. 堆排序
基本思想
- 事先声明:排升序用大根堆,排降序用小根堆 (默认为升序)
- 将待排序的 n 个数据使用向下调整造成一个大根堆,此时堆顶就是整个数组的最大值。
- 将堆顶和堆尾互换,此时堆尾的数就变成了最大值,剩余的待排序数组元素个数为 n - 1 个。
- 将剩余的 n - 1 个数调整回大根堆,将新的大根堆的新的堆顶和新的堆尾互换。
- 重复执行上述步骤,即可得到有序数组。
代码实现
//向下调整堆
void adjust_down(int data[], int size, int parent)
{int child = parent * 2 + 1; //假设是结点的左孩子比较大while (child < size){// 如果右孩子结点大于左孩子,则最大结点换成右孩子结点if (child + 1 < size && data[child + 1] > data[child]){child++;}// 最大孩子结点大于双亲结点if (data[child] > data[parent]){Swap(&data[child], &data[parent]);parent = child; // 双亲变成孩子结点child = parent * 2 + 1; // 孩子结点变成孙子结点}else{break;}}
}// 堆排序排成升序
void heap_sort(int data[], int n)
{int i = 0;int end = n - 1;// 从最后一个非叶子结点开始依次往前向下调整构建大根堆// n - 1 是最后一个结点的下标,(n - 1 - 1) / 2 是最后一个结点的夫结点下标// 也就是最后一个非叶子结点for (i = (n - 1 - 1) / 2; i >= 0; i--){// 要使用建大堆的向下调整算法adjust_down(data, n, i);}// 0 和 end 夹着的是待排序数据,end 是待排序数据的个数// 每次都选出一个最大的数放到 end 处,然后待排序数据个数 end - 1while (end > 0){Swap(&data[0], &data[end]); // 互换堆顶和堆尾的数据adjust_down(data, end, 0); // 从根位置 (0) 开始的向下调整end--; // 缩小待排序数据区间,且个数 - 1}
}
特性总结
- 时间复杂度:O(N * logN)
- 空间复杂度:O(1)
- 稳定性:不稳定排序
🌈 5. 冒泡排序
基本思想
- 每一趟将两两相邻的元素进行比较,小的放左边,大的放右边,按照递增来排序,不满足条件就交换数据,满足则不管。
- 将某个数排到最终的位置,这一轮叫一趟冒泡排序。
// 冒泡排序
void bubble_sort(int arr[], int n)
{for (int i = 0; i < n - 1; i++) // n 个元素需要进行 n-1 趟冒泡排序{int exchange = 1; // 用来判断某躺排序过程中是否发生交换for (int j = 0; j < n - 1 - i; j++) // 每一趟冒泡排序要比较 n-i-1 次{if (arr[j] > arr[j + 1]) // 升序时前一个大于后一个则交换数据{Swap(&data[j], &data[j + 1]);exchange = 0; // 发生交换就将其置为 0}}if(0 != exchange) // 如果 exchange 为真,则发生交换{break; // 未发生交换说明数据已经有序}}
}
特性总结
- 时间复杂度:最坏情况完全逆序时 O(N2);最好情况接近有序时 O(N)
- 空间复杂度:O(1)
- 稳定性:稳定排序
🌈 6. 快速排序
6.1 霍尔版快排
基本思想
- 选出一个关键值 key 作为基准值,将其排到最终位置将待排序数据划分成两半,左半边的值都 <= key,右半边的值都 >= key。
- 一般是用待排序数据的最左或最右的一个数作为关键值 key。
- 再定义一个 left 和 right,left 从从待排序数据的最左边开始从左向右走,right 从待排序数据的最右边开始从右向左走。
- 若选择最左边的数作为 key,则需要 right 先走,若选最右的则 left 先走。
- 如果 right 向左走过程中遇到了 < key 的数据,则停下让 left 开始向右走,直到 left 遇到第一个 > key 的数时,将 left 和 right 处的值交换,然后继续让 right 往左走。
- 重复执行第 3 步,直到 left 和 right 相遇为止,此时将相遇处的值和 key 交换即可。
- 此时已经使用 key 将整个序列划分成两个区域,左边的数都 < key,右边的则 > key。
- 对 key 划分的左右两半区域重复执行上述步骤,直到待排序区间的数据个数只有 0 / 1 个为止。
代码实现
// 快速排序(霍尔版)
void quick_sort_hoare(int data[], int begin, int end)
{if (begin >= end) // begin 大于 end 时无数据可排,等于时只有一个数据{return;}int left = begin; // left 用于从左往右找 > key 的数int right = end; // right 用于从右往左找 < key 的数int keyi = begin; // 将待排序区间的第一个数作为关键值 key, keyi 为 key 的下标while (left < right)// left == right 时相遇{// 让 right 先走使得 left 与 right 相遇处的值一定比 key 小// right 向前寻找 < 关键值的数,找不到则继续往前找,直到 left = right 为止while (left < right && data[right] >= data[keyi]){right--;}// left 向后寻找 > 关键值的数,找不到则继续往后找,直到 left = right 为止while (left < right && data[left] <= data[keyi]){left++;}// left 和 right 分别找到比 key 大和小的值,将小于 key 的换到左边,大于的换到右边Swap(&data[left], &data[right]); }// 将 left 与 right 最后相遇处的数据和关键值交换Swap(&data[left], &data[keyi]); // 交换完之后关键值的位置已经跑到原先 left 和 right 相遇的位置 keyi = left; quick_sort_hoare(data, begin, keyi - 1); // 对 keyi 的左半区执行上述步骤quick_sort_hoare(data, keyi + 1, end); // 对 keyi 的右半区执行上述步骤
}
6.2 挖坑版快排
基本思想
- 定义一个变量 key,将待排序区间的第一个数据交给 key,在该位置形成坑位 hole。
- 定义一个 left 和 right 变量分别执行待排序区间的最左和最右端。
- right 从右向左寻找 < key 的数据,找到时用该位置的值填补坑位 hole,然后将当前 right 所处的位置变成新的坑位 hole。
- left 从左向右寻找 > key 的数据,找到时用该位置的值填补坑位 hole,然后将当前 left 所处的位置变成新的坑位 hole。
- 重复执行第 2 和 3 步,直到 left 与 right 相遇时,将 key 里存的数放到相遇的位置。
- 此时 left 和 right 相遇的位置也将整个待排序数据划分成了两个区间,左区间都小于 key,右区间都大于 key。
- 对划分出的左右两个区间递归执行上述步骤,直到待排序区间的数据个数只有 0 / 1 个为止。
代码实现
// 快速排序(挖坑版)
void quick_sort_hole(int data[], int begin, int end)
{if (begin >= end) // 待排序区间没有或只有一个数据时则排序完成{return;}int key = data[begin]; // 存储第一个数为关键值int left = begin; // left 用于找大于 key 的数int right = end; // right 用于找小于 key 的数int holei = begin; // 存储坑位的下标while (left < right) // 未相遇时执行执行下列操作{// right 从右往左找 < key 的值,填到左边的坑while (left < right && data[right] >= key){right--;}data[holei] = data[right]; // 将找到的 < key 的值放到坑位中holei = right; // 当前 right 所处位置成了新的坑位// left 从左往右找 > key 的值,填到右边的坑while (left < right && data[left] <= key){left++;}data[holei] = data[left]; // 将找到的 > key 的值放到坑位中holei = left; // 当前 left 所处位置成了新的坑位}data[holei] = key; // 相遇时将 key 放到最终的坑位// 对坑位 holei 划分的的左右两半区域执行上述操作quick_sort_hole(data, begin, hole - 1);quick_sort_hole(data, hole + 1, end);
}
6.3 双指针快排
基本思想
- 选定待排序数据的第一个或最后一个数位关键值 key。
- 定义 prev 指针指向待排序数据开头,在定义个 cur 指针指向 prev + 1 的位置。
- 若 cur 指向的值 < key,则 prev++,然后交换 prev 和 cur 两个指针指向的内容,然后让 cur++;如果 cur 指向的内容 > key,则直接让 cur++。
- 该方法能直接让 < key 的值都放到最终 key 所在位置的左边。
- 重复执行第 3 步,直到 cur 走到了待排序区间的最末端时,将 key 和 prev 所指向的值互换。
- 此时 key 所处的位置同样将待排序区间分成了左右两部分,对这两部分重复指向上述操作。
代码实现
// 快速排序 (指针版)
void quick_sort_pointer(int data[], int begin, int end)
{if (begin >= end) // 待排序区间数据个数为 0 / 1 时排序结束{return;}int keyi = begin;int prev = begin; int cur = prev + 1;while (cur <= end) // cur 不能越界{// cur 指向的值小于 key,且 prev 向后走一步后不等于 cur (否则就是原地交换)if (data[cur] < data[keyi] && ++prev != cur) {Swap(&data[prev], &data[cur]); // 交换 prev 和 cur 指向的值}cur++; // 最后 cur 都是要往后走一步的}Swap(&data[keyi], &data[prev]); // 将关键值和 prev 最后指向的值交换keyi = prev; // 交换后关键值的位置也会变quick_sort_pointer(data, begin, keyi - 1); // 对 key 的左半边执行上述操作quick_sort_pointer(data, keyi + 1, end); // 对 key 的右半边执行上述操作
}
6.4 非递归快排
基本思想
- 定义一个栈,用于存储待排序数据左右两端数据的下标。
- 首先将待排序数据两端的下标 begin 和 end 入栈。
- 然后将 begin 和 end 出栈,然后对 begin 和 end 夹着的区间进行单趟快排 (这里采用双指针法进行单趟排序),将 key 排到最终位置,然后获取 key 的下标。
- key 将待排序数据分成了两个区间,为了符合栈的定义想先排序 key 的左区间则要先将右区间 [keyi + 1, end] 入栈,再将左区间 [begin, keyi - 1] 入栈。
- 将左区间出栈,再对该区间重复执行 2 ~ 4 步,直到最开始划分的左区间全部排完,然后才能对一开始划分出的右区间执行上述步骤。
// 这里就使用双指针法进行单趟排序,其他两种方法也可以使用
int part_sort(int data[], int begin, int end)
{if (begin >= end){return;}int keyi = begin;int prev = begin; int cur = prev + 1;while (cur <= end){if (data[cur] < data[keyi] && ++prev != cur) {Swap(&data[prev], &data[cur]); }cur++; }Swap(&data[keyi], &data[prev]);return prev; // 返回关键之下标
} void quick_sort_nonr(int data[], int begin, int end)
{st s; // 定义栈空间st_init(&s) // 初始化栈空间st_push(&s,end); // 先入区间右端st_push(&s, begin); // 再入区间左端while (!st_empty(&s)) // 栈为空时排序结束{int left = st_top(&s); // 先出区间左端st_pop(&s);int right = st_top(&s); // 再出区间右端st_pop(&s);// 然后对该区间进行单趟排序,再获取关键值的下标int keyi = part_sort(data, left, right);// keyi 将待排序数据划分成两端区间// [left, keyi - 1] keyi [keyi + 1, right]if (left < keyi - 1) // 左区间还有 1 个以上的值{st_push(&s, keyi - 1); // keyi 左区间的 右端 入栈st_push(&s, left); // keyi 左区间的 左端 入栈}if (keyi + 1 < right) // 右区间还有 1 个以上的值{st_push(&s, right); // keyi 右区间的 右端 入栈st_push(&s, keyi + 1); // keyi 右区间的 左端 入栈}}
}
🌈 7. 归并排序
基本思想
归并排序的本质思想就是分治
- 分:将一个大的待排序序列拆分成两个小的待排序序列。
- 治:将两个小的有序序列合并成一个大的有序序列。
基本步骤
- 将待排序序列拆分成两个待排序子序列,然后对拆分出的每个待排序子序列执行同样步骤,直到被拆分出的子序列中只有一个元素为止,此时只有一个元素的子序列必定有序。
- 将两个有序子序列排序合并,合成一个新的有序子序列,重复该步骤,直到待排序的序列只有一个为止,此时所有的数据已经排好序了。
- 上述步骤需要借助一个和原数组等长的 tmp 数组来暂时存储分出来的子序列。
7.1 递归版归并
// 归并排序子函数
void _merge_sort(int data[], int begin, int end, int tmp[])
{if (begin >= end) // 区间数据个数为 0 / 1 时有序{return;}int mid = begin + (end - begin) / 2; // 记录每个区间的中间位置// 使用后序的方式递归拆分数据,递归完回来的时候该区间是有序的// 将区间划分为 [begin,mid][mid + 1,end] 两部分_merge_sort(data, begin, mid, tmp); // 递归划分左区间_merge_sort(data, mid + 1, end, tmp); // 递归划分右区间// 合并 (归并) 数据int begin1 = begin, end1 = mid; // 左区间int begin2 = mid + 1, end2 = end; // 右区间int i = begin;// 两个区间有一个区间将所有的值都尾插到 tmp 时结束循环while (begin1 <= end1 && begin2 <= end2){// 取两个区间对应位置的较小值尾插到 tmp 数组if (data[begin1] < data[begin2]){tmp[i++] = data[begin1++];}else{tmp[i++] = data[begin2++];}}// 尾插完时肯定有一个区间不为空,直接将其放到 tmp 后面while (begin1 <= end1) // 左区间如果不为空时{tmp[i++] = data[begin1++];}while (begin2 <= end2) // 右区间如果不为空时{tmp[i++] = data[begin2++];}// 从 begin 处开始将归并好后的数据拷贝回原数组memcpy(data + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}// 归并排序 (递归版)
void merge_sort(int data[], int n)
{int* tmp = (int*)malloc(n * sizeof(int)); // 暂时存储归并后的数据assert(tmp);_merge_sort(data, 0, n - 1, tmp); // 待拆分区间下标为 0 到 n - 1free(tmp);
}
7.2 迭代版归并
// 归并排序 (非递归)
void merge_sort_non_r(int data[], int n)
{int* tmp = (int*)malloc(sizeof(int) * n);assert(tmp);int gap = 1; // 每组要归并的元素数量,从 1 开始,以 2^n 递增while (gap < n) // gap < n 时说明还有值待排序{for (int i = 0; i < n; i += 2 * gap){// 两组归并数据的范围: [begin1, end1][begin2, end2]int begin1 = i, end1 = i + gap - 1;`在这里插入代码片`int begin2 = i + gap, end2 = i + 2 * gap - 1;// 防止数组越界, end1、begin2、end2 都有可能越界if (end1 >= n || begin2 >= n){break;}if (end2 >= n){end2 = n - 1; // end2 不管最后越界到哪,都必须修正为最后一个元素}int j = begin1;while (begin1 <= end1 && begin2 <= end2){// 取两个区间对应位置的较小值尾插到 tmp 数组if (data[begin1] < data[begin2]){tmp[j++] = data[begin1++];}else{tmp[j++] = data[begin2++];}}// 尾插完时有个区间肯定不为空,直接接到 tmp 后面while (begin1 <= end1){tmp[j++] = data[begin1++];}while (begin2 <= end2){tmp[j++] = data[begin2++];}// 将归并好的数据拷贝回原数组memcpy(data + i, tmp + i, sizeof(int) * (end2 - i + 1));}gap *= 2;}free(tmp);tmp = NULL;
}
🌈 8. 计数排序
基本思想
- 计数排序的原理采用了哈希的思想,将待排序数据的值作为关键值存储在对应下标处,然后统计每个值出现的次数依次排序。
基本步骤
- 定义一个 count 数组初始化成全 0 用来记录待排序的每个数据的出现次数。
- 从头到尾遍历一遍待排序序列,序列内每出现一个值就将该值作为 count 数组内对应下标,将对应下标处的值 + 1.
- 如: 序列中每出现一个数字 5,就将 count 数组下标为 5 的值加 1 count[5]++
- 用 count 数组统计完了待排序序列内所有数据的出现次数以后,在 count 数组下标处的值为几,就将原数组覆盖几个值。
- 如: count[1] = 3,表示原数组有 3 个 1 ,就将原数组的前三个值覆盖为 1,count 数组内出现 0 则不管
算法优化
- 上述动图采用绝对映射的方法来演示,即完全 count 数组计数的下标完全采用原数组内的值。
- 待排序数据中出现一个 1 就在 count 数组下标 1 处 +1,出现一个 7 就在下标 7 处 + 1。
- 绝对映射的缺点就在于,如果序列最小值为 10w,从下标 10w 开始计数,此时 count 数组有 10w 个空间就会被浪费掉,并且绝对映射没办法对负数进行排序,此时就要使出相对映射了。
- 相对映射:求出序列的最小值 min 和最大值 max,为 count 数组开辟 max - min + 1 个空间即可,再将序列中的每个数 key 存放在 count 数组 key - min 下标处即可, 排序时将 count 数组中不为 0 处的 下标 + min 即可还原给原数组。
代码实现
// 计数排序
void count_sort(int data[], int n)
{int i = 0;int j = 0;int min = data[0]; // 记录最小值int max = data[0]; // 记录最大值// 先求 data 数组中的最大和最小值for (i = 1; i < n; i++){if (min > data[i]){min = data[i];}if (max < data[i]){max = data[i];}}int range = max - min + 1; // count 数组的范围int* count = (int*)calloc(range, sizeof(int));assert(count);// 使用相对映射统计 data 数组中每个数据的出现次数for (i = 0; i < n; i++){count[data[i] - min]++; }// 排序: 在 count 数组下标处的值为几,就将原数组覆盖几个值i = 0;for (j = 0; j < range; j++){while (count[j]--){data[i++] = j + min;}}free(count);count = NULL;
}
相关文章:

【数据结构初阶 9】内排序
文章目录 🌈 1. 直接插入排序🌈 2. 希尔排序🌈 3. 简单选择排序🌈 4. 堆排序🌈 5. 冒泡排序🌈 6. 快速排序6.1 霍尔版快排6.2 挖坑版快排6.3 双指针快排6.4 非递归快排 🌈 7. 归并排序7.1 递归版…...

后端八股笔记------Redis
Redis八股 上两种都有可能导致脏数据 所以使用两次删除缓存的技术,延时是因为数据库有主从问题需要更新,无法达到完全的强一致性,只能达到控制一致性。 一般放入缓存中的数据都是读多写少的数据 业务逻辑代码👇 写锁Ǵ…...
HarmonyOS通过 axios发送HTTP请求
我之前的文章 HarmonyOS 发送http网络请求 那么今天 我们就来说说axios 这个第三方工具 想必所有的前端开发者都不会陌生 axios 本身也属于 HTTP请求 所以鸿蒙开发中也支持它 但首先 想在HarmonyOS中 使用第三方工具库 就要先下载安装 ohpm 具体可以参考我的文章 HarmonyOS 下…...
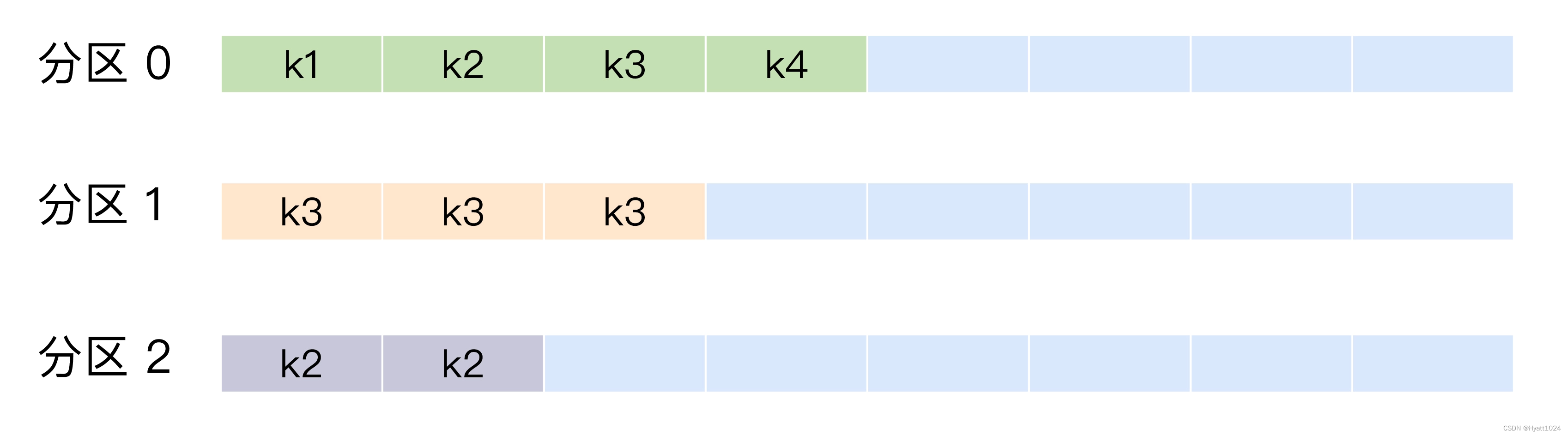
【Kafka系列 08】生产者消息分区机制详解
一、前言 我们在使用 Apache Kafka 生产和消费消息的时候,肯定是希望能够将数据均匀地分配到所有服务器上。 比如很多公司使用 Kafka 收集应用服务器的日志数据,这种数据都是很多的,特别是对于那种大批量机器组成的集群环境,每分…...

【PyTorch】进阶学习:BCEWithLogitsLoss在多标签分类任务中的正确使用---logits与标签形状指南
【PyTorch】进阶学习:BCEWithLogitsLoss在多标签分类任务中的正确使用—logits与标签形状指南 🌈 个人主页:高斯小哥 🔥 高质量专栏:Matplotlib之旅:零基础精通数据可视化、Python基础【高质量合集】、PyTo…...

ocr关键信心提取数据集
doc/doc_ch/dataset/kie_datasets.md PaddlePaddle/PaddleOCR - Gitee.com https://huggingface.co/datasets/howard-hou/OCR-VQA OCR-VQA Dataset | Papers With Code...
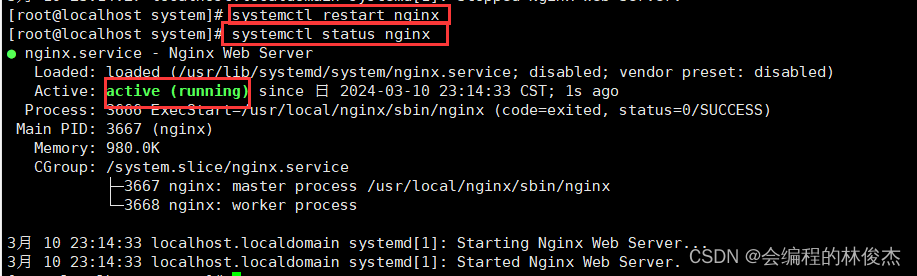
Linux中,配置systemctl操作Nginx
最近在通过Linux系统学一些技术,但是在启动Nginx时,总是需要执行其安装路径下的脚本文件,要么我们需要先进入其安装路径,要么我们每次执行命令直接拼上Nginx的完整目录,如启动时命令为/usr/local/nginx/sbin/nginx。 可…...
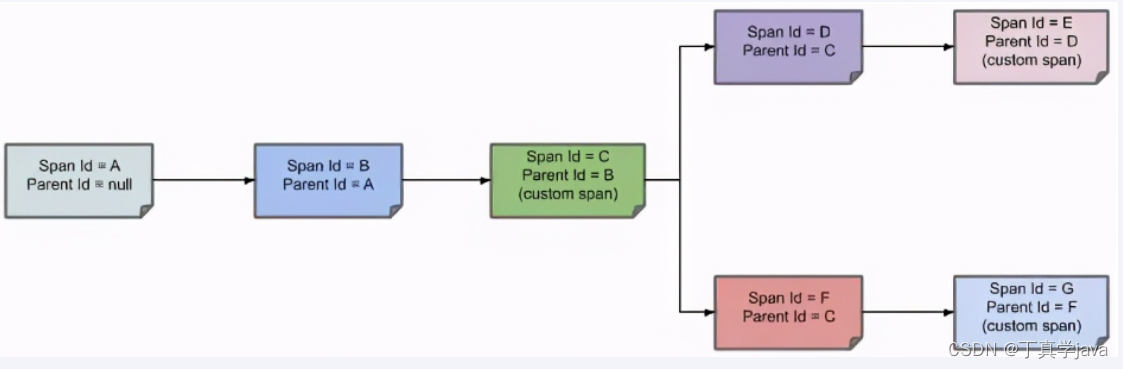
Sleuth(Micrometer)+ZipKin分布式链路追踪
Sleuth(Micrometer)ZipKin分布式链路追踪 Micrometer springboot3之前还可以用sleuth,springboot3之后就被Micrometer所替代 官网https://github.com/spring-cloud/spring-cloud-sleuth 为什么会出现这个技术? 在微服务框架中,一个由客户…...

fanout模式
生产者: public class Provider {public static void main(String[] args) throws IOException {Connection connection RabbitMQUtils.getConnection();Channel channel connection.createChannel();//通道声明指定的交换机 参数1:交换机名称 参数2&…...

Docker基础—CentOS中卸载Docker
要卸载已经安装好的 Docker,可以按照以下步骤进行: 1 停止正在运行的 Docker 服务 sudo systemctl stop docker 2 卸载 Docker 软件包 sudo yum remove docker-ce 3 删除 Docker 数据和配置文件(可选) sudo rm -rf /var/lib…...

深入解读 Elasticsearch 磁盘水位设置
本文将带你通过查看 Elasticsearch 源码来了解磁盘使用阈值在达到每个阶段的处理情况。 跳转文章末尾获取答案 环境 本文使用 Macos 系统测试,512M 的磁盘,目前剩余空间还有 60G 左右,所以按照 Elasticsearch 的设定,ES 中分片应…...
M1电脑 Xcode15升级遇到的问题
遇到四个问题 一、模拟器下载经常报错。 二、Xcode15报错: SDK does not contain libarclite 三、报错coreAudioTypes not found 四、xcode模拟器运行一次下次必定死机 一、模拟器下载经常报错。 可以https://developer.apple.com/download/all/?qios 下载最新的模拟器&…...
)
软考 系统架构设计师之回归及知识点回顾(3)
接前一篇文章:软考 系统架构设计师之回归及知识点回顾(2) 继续回顾一下之前已经介绍和讲解过的系统架构设计师中的知识点: 7. 净室软件工程 净室(Cleaning Room)软件工程是一种应用数学与统计学理论&…...

探索stable diffusion的奇妙世界--01
目录 1. 理解prompt提示词: 2. Prompt中的技术参数: 3. Prompt中的Negative提示词: 4. Prompt中的特殊元素: 5. Prompt在stable diffusion中的应用: 6. 作品展示: 在AI艺术领域,stable di…...

C语言数组的维数该如何理解?
一、问题 什么叫做维,维是不是数组中数的个数呢? 二、解答 维数是数组元素的下标个数。使⽤数组的时候,如果只有⼀个下标,则称为⼀维数组,⼀维数组⼀般表示⼀种线性数据的组合。⼆维数组则是有两个下标,可…...
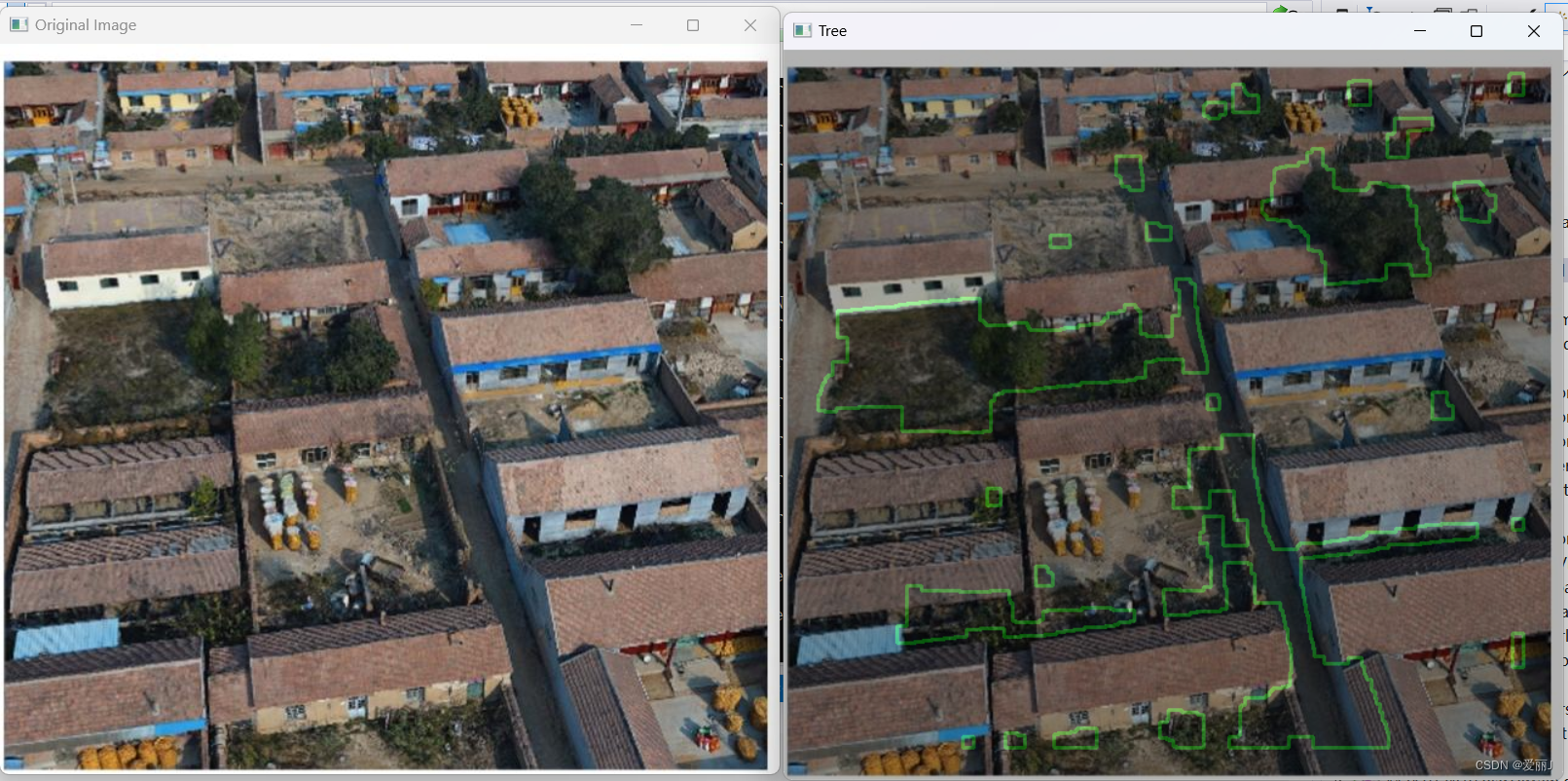
opencv解析系列 - 基于DOM提取大面积植被(如森林)
Note:简单提取,不考虑后处理(填充空洞、平滑边界等) #include <iostream> #include "opencv2/imgproc.hpp" #include "opencv2/highgui.hpp" #include <opencv2/opencv.hpp> using namespace cv…...

【Leetcode】299. 猜数字游戏
文章目录 题目思路代码结果 题目 题目链接 你在和朋友一起玩 猜数字(Bulls and Cows)游戏,该游戏规则如下: 写出一个秘密数字,并请朋友猜这个数字是多少。朋友每猜测一次,你就会给他一个包含下述信息的提…...

JWT身份验证
在实际项目中一般会使用jwt鉴权方式。 JWT知识点 jwt,全称json web token ,JSON Web令牌是一种开放的行业标准RFC 7519方法,用于在两方安全地表示声明。具体网上有许多文章介绍,这里做简单的使用。 1.数据结构 JSON Web Token…...

IOS面试题object-c 71-80
71. 简单介绍下NSURLConnection类及 sendSynchronousRequest:returningResponse:error:与– initWithRequest:delegate:两个方法的区别?NSURLConnection 主要用于网络访问,其中 sendSynchronousRequest:returningResponse:error:是同步访问数据,即当前…...

计算机mfc140.dll文件缺失的修复方法分析,一键修复mfc140.dll
电脑显示mfc140.dll文件缺失信息时,不必担心,这通常是个容易解决的小问题。接下来让我们详细探究并解决mfc140.dll文件缺失的状况。以下将详述相应的解决方案,从而帮助您轻松克服这一技术难题。通过几个简单步骤,即可恢复正常使用…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...










