序列的第 k 个数(c++题解)
题目描述
BSNY 在学等差数列和等比数列,当已知前三项时,就可以知道是等差数列还是等比数列。现在给你序列的前三项,这个序列要么是等差序列,要么是等比序列,你能求出第 m项的值吗。 如果第 项的值太大,对 200907取模。
输入格式
第一行一个整数 ,表示有 组测试数据;
对于每组测试数据,输入前三项 ,然后输入 。
数据保证a,b,c都是整数。数据保证若序列为等比序列则公比为整数。
输出格式
对于每组数据输出第 项的值,对 取模。
样例
样例输入
复制2
1 2 3 5
1 2 4 5
样例输出
复制5
16
样例说明
第一组是等差序列,第二组是等比数列。
_____________________________________________________________________________
写作不易,点个赞呗!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
_____________________________________________________________________________
#include <bits/stdc++.h>
using namespace std;
long long f(long long n,long long a){if(n==1)return a;if(n==0)return 1;long long x=f(n/2,a)%200907;if(n%2==0)return x*x%200907;else return a*x*x%200907;
}
long long a,b,c,n,k,ans;
int main() { cin>>n;for(long long i=1;i<=n;i++){cin>>a>>b>>c>>k;if(b-a==c-b&&b!=a){long long idx=b-a;ans=a;ans=(ans+idx*(k-1))%200907;cout<<ans<<endl;}else{long long idx=b/a;ans=a;cout<<ans%200907*f(k-1,idx)%200907<<endl;}}
}相关文章:
)
序列的第 k 个数(c++题解)
题目描述 BSNY 在学等差数列和等比数列,当已知前三项时,就可以知道是等差数列还是等比数列。现在给你序列的前三项,这个序列要么是等差序列,要么是等比序列,你能求出第 m项的值吗。 如果第 项的值太大,对…...
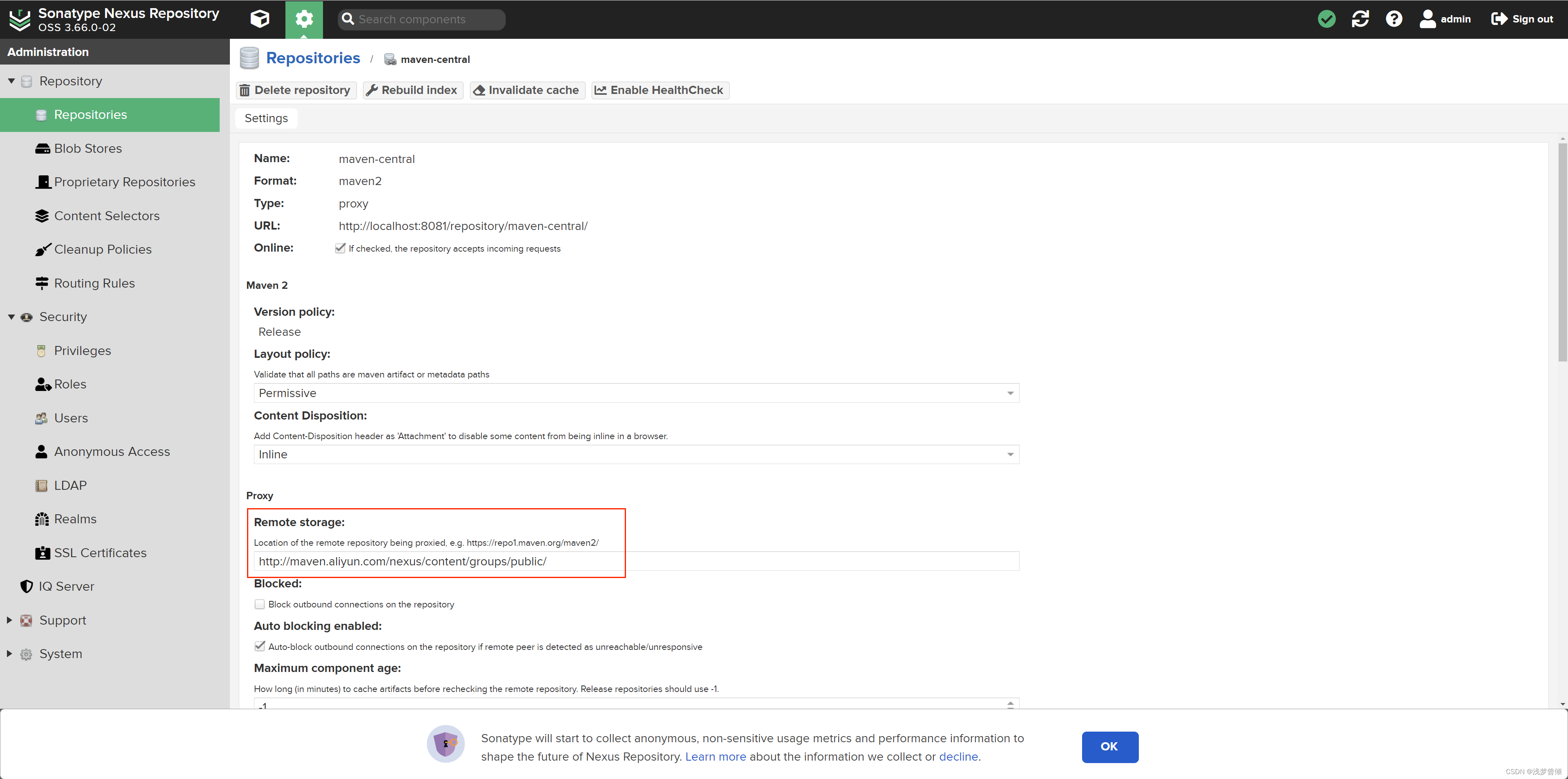
Nexus - Maven私服构建和使用
文章目录 1. Maven 私服简介2. Nexus下载安装3. 如何使用Nexus私服3.1 通过Nexus下载Jar包3.2 将Jar包部署到Nexus3.3 引用别人部署的jar包 1. Maven 私服简介 Maven 私服是一种特殊的Maven远程仓库,它是架设在局域网内的仓库服务,用来代理位于外部的远…...

SpringMVC09、Ajax
9、Ajax 9.1、简介 AJAX Asynchronous JavaScript and XML(异步的 JavaScript 和 XML)。 AJAX 是一种在无需重新加载整个网页的情况下,能够更新部分网页的技术。 Ajax 不是一种新的编程语言,而是一种用于创建更好更快以及交互…...

【数据结构初阶 9】内排序
文章目录 🌈 1. 直接插入排序🌈 2. 希尔排序🌈 3. 简单选择排序🌈 4. 堆排序🌈 5. 冒泡排序🌈 6. 快速排序6.1 霍尔版快排6.2 挖坑版快排6.3 双指针快排6.4 非递归快排 🌈 7. 归并排序7.1 递归版…...

后端八股笔记------Redis
Redis八股 上两种都有可能导致脏数据 所以使用两次删除缓存的技术,延时是因为数据库有主从问题需要更新,无法达到完全的强一致性,只能达到控制一致性。 一般放入缓存中的数据都是读多写少的数据 业务逻辑代码👇 写锁Ǵ…...
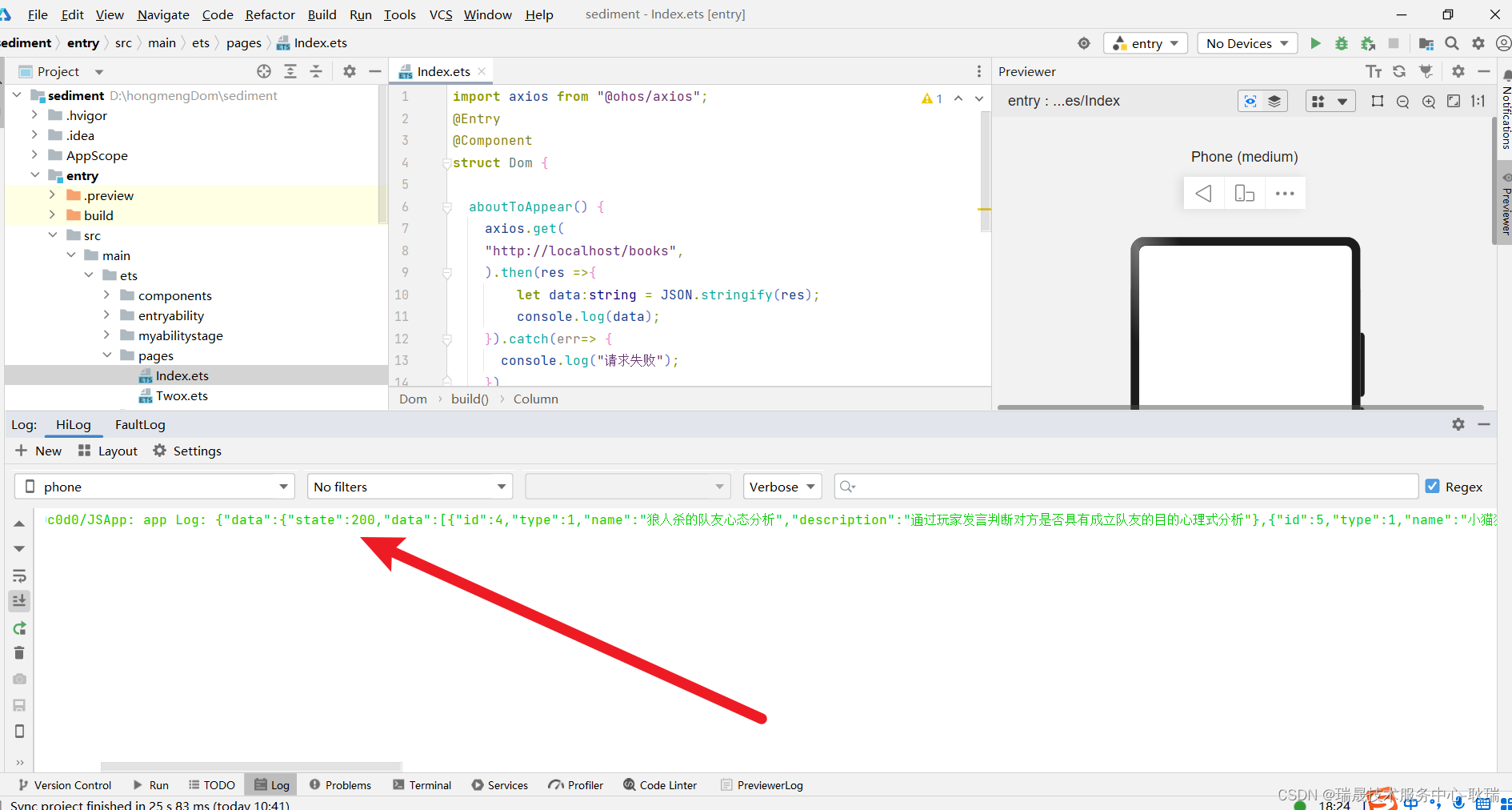
HarmonyOS通过 axios发送HTTP请求
我之前的文章 HarmonyOS 发送http网络请求 那么今天 我们就来说说axios 这个第三方工具 想必所有的前端开发者都不会陌生 axios 本身也属于 HTTP请求 所以鸿蒙开发中也支持它 但首先 想在HarmonyOS中 使用第三方工具库 就要先下载安装 ohpm 具体可以参考我的文章 HarmonyOS 下…...
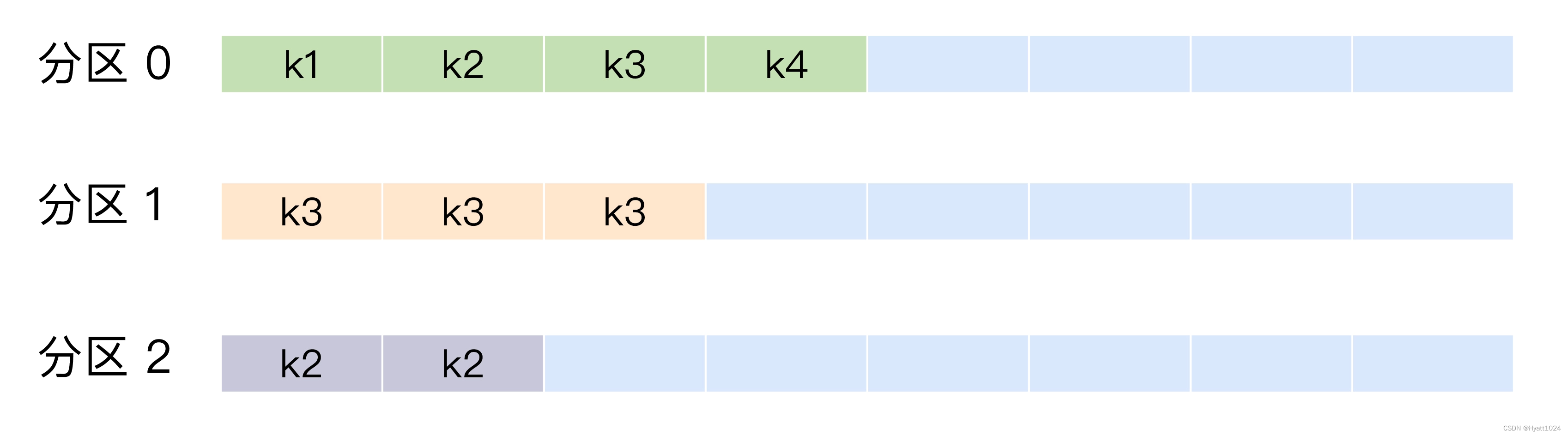
【Kafka系列 08】生产者消息分区机制详解
一、前言 我们在使用 Apache Kafka 生产和消费消息的时候,肯定是希望能够将数据均匀地分配到所有服务器上。 比如很多公司使用 Kafka 收集应用服务器的日志数据,这种数据都是很多的,特别是对于那种大批量机器组成的集群环境,每分…...

【PyTorch】进阶学习:BCEWithLogitsLoss在多标签分类任务中的正确使用---logits与标签形状指南
【PyTorch】进阶学习:BCEWithLogitsLoss在多标签分类任务中的正确使用—logits与标签形状指南 🌈 个人主页:高斯小哥 🔥 高质量专栏:Matplotlib之旅:零基础精通数据可视化、Python基础【高质量合集】、PyTo…...

ocr关键信心提取数据集
doc/doc_ch/dataset/kie_datasets.md PaddlePaddle/PaddleOCR - Gitee.com https://huggingface.co/datasets/howard-hou/OCR-VQA OCR-VQA Dataset | Papers With Code...
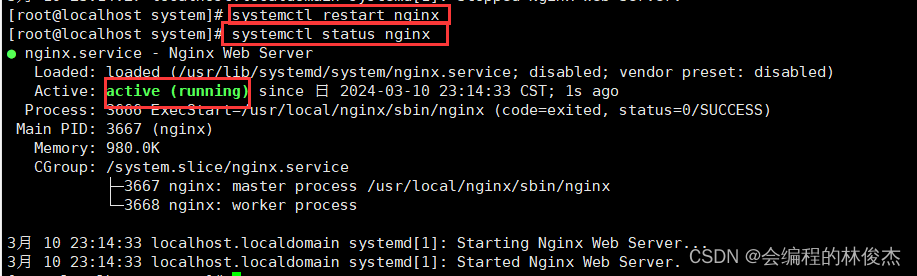
Linux中,配置systemctl操作Nginx
最近在通过Linux系统学一些技术,但是在启动Nginx时,总是需要执行其安装路径下的脚本文件,要么我们需要先进入其安装路径,要么我们每次执行命令直接拼上Nginx的完整目录,如启动时命令为/usr/local/nginx/sbin/nginx。 可…...
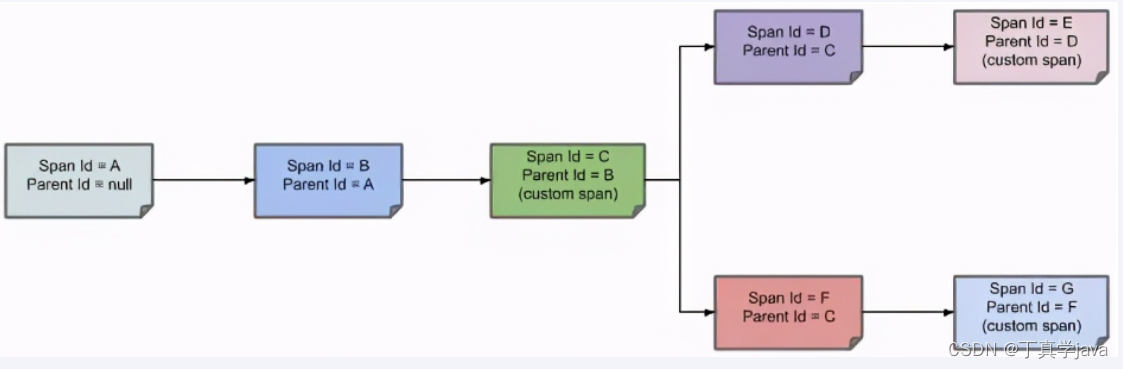
Sleuth(Micrometer)+ZipKin分布式链路追踪
Sleuth(Micrometer)ZipKin分布式链路追踪 Micrometer springboot3之前还可以用sleuth,springboot3之后就被Micrometer所替代 官网https://github.com/spring-cloud/spring-cloud-sleuth 为什么会出现这个技术? 在微服务框架中,一个由客户…...

fanout模式
生产者: public class Provider {public static void main(String[] args) throws IOException {Connection connection RabbitMQUtils.getConnection();Channel channel connection.createChannel();//通道声明指定的交换机 参数1:交换机名称 参数2&…...

Docker基础—CentOS中卸载Docker
要卸载已经安装好的 Docker,可以按照以下步骤进行: 1 停止正在运行的 Docker 服务 sudo systemctl stop docker 2 卸载 Docker 软件包 sudo yum remove docker-ce 3 删除 Docker 数据和配置文件(可选) sudo rm -rf /var/lib…...

深入解读 Elasticsearch 磁盘水位设置
本文将带你通过查看 Elasticsearch 源码来了解磁盘使用阈值在达到每个阶段的处理情况。 跳转文章末尾获取答案 环境 本文使用 Macos 系统测试,512M 的磁盘,目前剩余空间还有 60G 左右,所以按照 Elasticsearch 的设定,ES 中分片应…...
M1电脑 Xcode15升级遇到的问题
遇到四个问题 一、模拟器下载经常报错。 二、Xcode15报错: SDK does not contain libarclite 三、报错coreAudioTypes not found 四、xcode模拟器运行一次下次必定死机 一、模拟器下载经常报错。 可以https://developer.apple.com/download/all/?qios 下载最新的模拟器&…...
)
软考 系统架构设计师之回归及知识点回顾(3)
接前一篇文章:软考 系统架构设计师之回归及知识点回顾(2) 继续回顾一下之前已经介绍和讲解过的系统架构设计师中的知识点: 7. 净室软件工程 净室(Cleaning Room)软件工程是一种应用数学与统计学理论&…...

探索stable diffusion的奇妙世界--01
目录 1. 理解prompt提示词: 2. Prompt中的技术参数: 3. Prompt中的Negative提示词: 4. Prompt中的特殊元素: 5. Prompt在stable diffusion中的应用: 6. 作品展示: 在AI艺术领域,stable di…...

C语言数组的维数该如何理解?
一、问题 什么叫做维,维是不是数组中数的个数呢? 二、解答 维数是数组元素的下标个数。使⽤数组的时候,如果只有⼀个下标,则称为⼀维数组,⼀维数组⼀般表示⼀种线性数据的组合。⼆维数组则是有两个下标,可…...
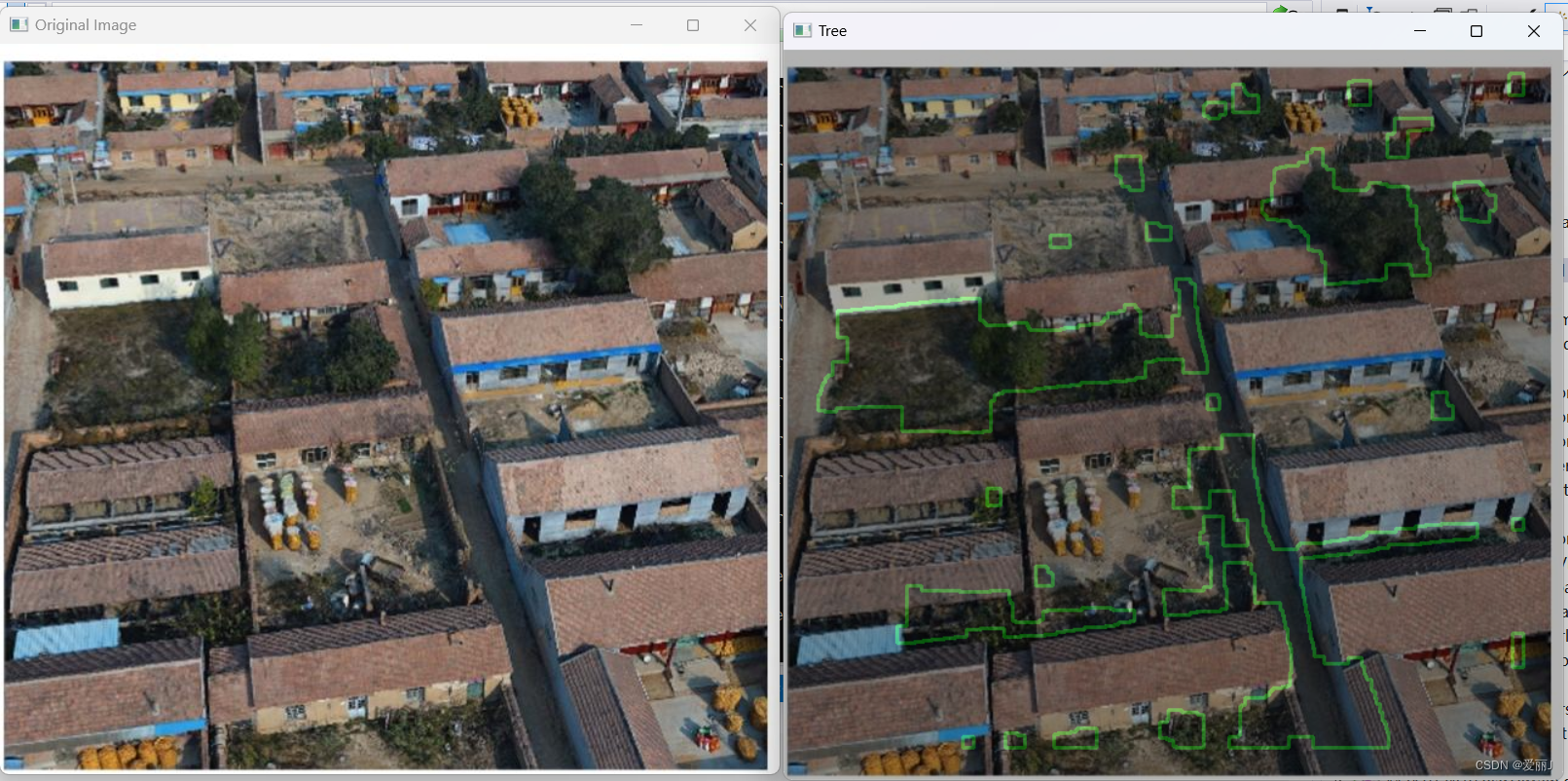
opencv解析系列 - 基于DOM提取大面积植被(如森林)
Note:简单提取,不考虑后处理(填充空洞、平滑边界等) #include <iostream> #include "opencv2/imgproc.hpp" #include "opencv2/highgui.hpp" #include <opencv2/opencv.hpp> using namespace cv…...

【Leetcode】299. 猜数字游戏
文章目录 题目思路代码结果 题目 题目链接 你在和朋友一起玩 猜数字(Bulls and Cows)游戏,该游戏规则如下: 写出一个秘密数字,并请朋友猜这个数字是多少。朋友每猜测一次,你就会给他一个包含下述信息的提…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...
