力扣hot100:152.乘积最大子数组(动态规划)

一个子数组问题,我们要使用线性dp,最好先考虑以i结尾,如果定义dp[i]为前i个数最大子数组乘积值 那么dp[i-1]就无法转移到dp[i]。因此我们先考虑dp[i]定义为以第i个数结尾的最大子数组乘积值。
53. 最大子数组和
最大子数组和是一个动态规划问题,定义dp[i]表示以nums[i]结尾的最大子数组和,那么dp[i]=max(dp[i-1]+nums[i],nums[i])。对于这里乘积最大子数组和,我们也有这样的想法,但是由于负负得正,如{-3,2,3,-2},dp[2]=6,nums[3]=-2,但是dp[3]不是-2,而应当乘以前面的-3。
记录前一个负数位置的动态规划
一个朴素的想法就是:
记录前一个负数的位置,这样遍历到一个负数时,我们在前一个负数到这个负数之间的数都是≥0的,这样在遇到负数时的连乘最大值应当至少是前一个负数连乘到这个负数,而当 以 前一个负数的 前一个数为结尾的子数组乘积为正时,也应该考虑进去。这样负数的情况就考虑完了。当之前没有负数时,有0时dp[i]就是0,没有0时dp[i]就是该负数。
当遇到的是一个正数,则只需要使用dp[i]=max(dp[i-1]*nums[i],nums[i]),因为以该正数结尾的最大连乘,要么是本身,要么以 前一个数结尾的子数组连乘为正*该正数。
class Solution {
public:int maxProduct(vector<int>& nums) {vector<int> dp(nums.size());int ans;ans=dp[0]=nums[0];int minus=-1;if(nums[0]<0) minus=0;int flag=0;//记录前一个负数到这个负数是否存在0for(int i=1;i<nums.size();++i){dp[i]=1;if(nums[i]==0) flag=1;if(nums[i]<0){if(minus>=0){//中间有0也应该是0if(minus>0&&dp[minus-1]>0)dp[i]=dp[minus-1]*nums[minus]*nums[i];else dp[i]=nums[minus]*nums[i];if(minus!=i-1) {if(dp[minus]<=0)dp[i]*=dp[i-1];else dp[i]*=dp[i-1]/dp[minus];}if(flag) dp[i]=0;}else dp[i]=nums[i];minus=i;flag=0;}else dp[i]=dp[i-1]>0?dp[i-1]*nums[i]:nums[i];if(dp[i]>ans) ans=dp[i];}//cout<<dp[nums.size()-2];return ans;}
};
//dp[i]表示以i结尾的子数组的乘积最大值记录最大最小的动态规划
进阶的考虑:
当遇到负数时,我们能不能让 以它前一个数结尾的连乘 负得更多,这样我们再乘上这个数就大的更多。
当遇到正数时,我们依然让 以前一个数结尾的连乘 正的更多即可。
因此,我们可以保存一个最小值和最大值。
最小值让以第i个数结尾的子数组连乘最小,
最大值让以第i个数结尾的子数组连乘最大,
最小值的计算和最大值的计算,前一两者同时考虑就把正负给抵消掉了。
class Solution {
public:int maxProduct(vector<int>& nums) {int mx=nums[0];int mn=nums[0];int ans=nums[0];for(int i=1;i<nums.size();++i){int Max=mx,Min=mn;mx=max(max(Max*nums[i],Min*nums[i]),nums[i]);mn=min(min(Min*nums[i],Max*nums[i]),nums[i]);ans=ans>mx?ans:mx;}return ans;}
};
相关文章:

力扣hot100:152.乘积最大子数组(动态规划)
一个子数组问题,我们要使用线性dp,最好先考虑以i结尾,如果定义dp[i]为前i个数最大子数组乘积值 那么dp[i-1]就无法转移到dp[i]。因此我们先考虑dp[i]定义为以第i个数结尾的最大子数组乘积值。 53. 最大子数组和 最大子数组和是一个动态规划问…...

【python 】----Pytest基础知识与进阶知识
定义 用于编写和执行Python测试全功能测试框架(工具),是一个第三方库 安装 pip insatll pytest 安装pytest --version 校验 pytest的组成构成 不写调用语句也可以执行函数内容 在用例运行语句里面: -s:指的是开启与终端的交互,如果没有-s(程序不会输入与打印),一条用…...
谷歌开源的LLM大模型 Gemma 简介
相关链接: Hugging face模型下载地址:https://huggingface.co/google/gemma-7bGithub地址:https://github.com/google/gemma_pytorch论文地址:https://storage.googleapis.com/deepmind-media/gemma/gemma-report.pdf官方博客&…...

深入理解 Vuex:从基础到应用场景
前言 在之前的文章中,我们已经对 Vue.js 有了一定的了解。今天我们要对Vue官方的状态共享管理器Vuex进行详细讲解,将其基本吃透,目标是面对大多数业务需求; 一、介绍 Vuex 是一个专为 Vue.js 应用程序开发的状态管理模式。它采用…...

自定义 classNames hooks
什么是自定义 hooks 自定义hooks是react提供的编写公共函数的方法 自定hooks 和 通用函数的区别 一定有人会说 hooks 可以使用react 的方法,但是公共函数也可以,因为 jsx 语法的原因 函数必须开头进行大写 其实这些都是 react 的语法规范ÿ…...

玩转centos 下的core 文件
玩转centos 下的core 文件 ------------------------------------------------------------ author: hjjdebug date: 2024年 03月 06日 星期三 12:38:35 CST description: 玩转centos 下的core 文件 ------------------------------------------------------------ 一: 准备一…...
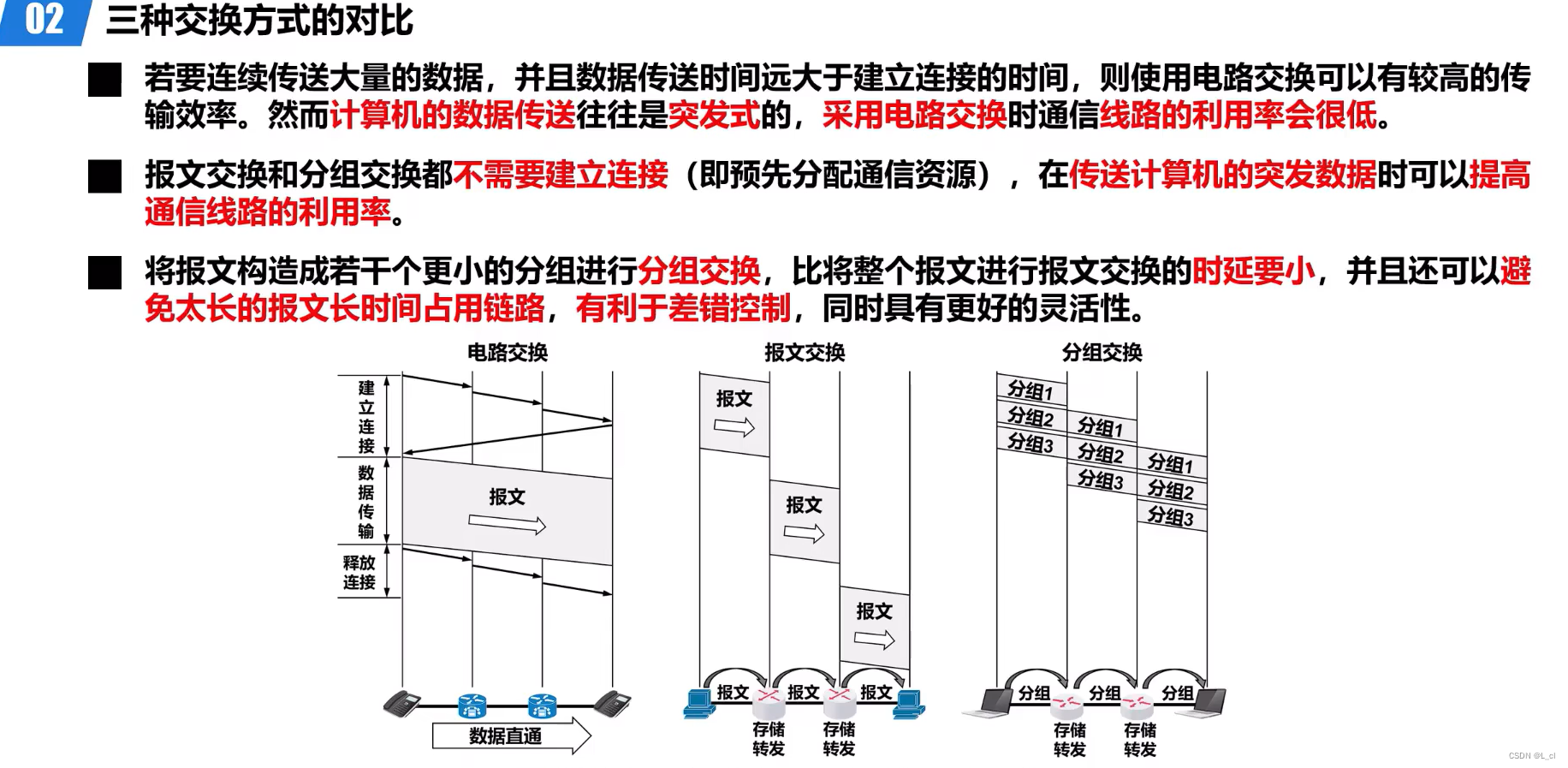
深入浅出计算机网络 day.1 概论③ 电路交换、分组交换和报文交换
人无法同时拥有青春和对青春的感受 —— 04.3.9 内容概述 01.电路交换、分组交换和报文交换 02.三种交换方式的对比 一、电路交换、分组交换和报文交换 1.电路交换 计算机之间的数据传送是突发式的,当使用电路交换来传送计算机数据时,其线路的传输效率一…...

linux:线程的控制
个人主页 : 个人主页 个人专栏 : 《数据结构》 《C语言》《C》《Linux》 文章目录 前言一、线程的总结1. 线程的优点2. 线程的缺点3. 线程异常4.线程和进程 二、线程的控制创建线程线程终止线程等待获取返回值 线程分离 总结 前言 本文作为我对于线程的…...
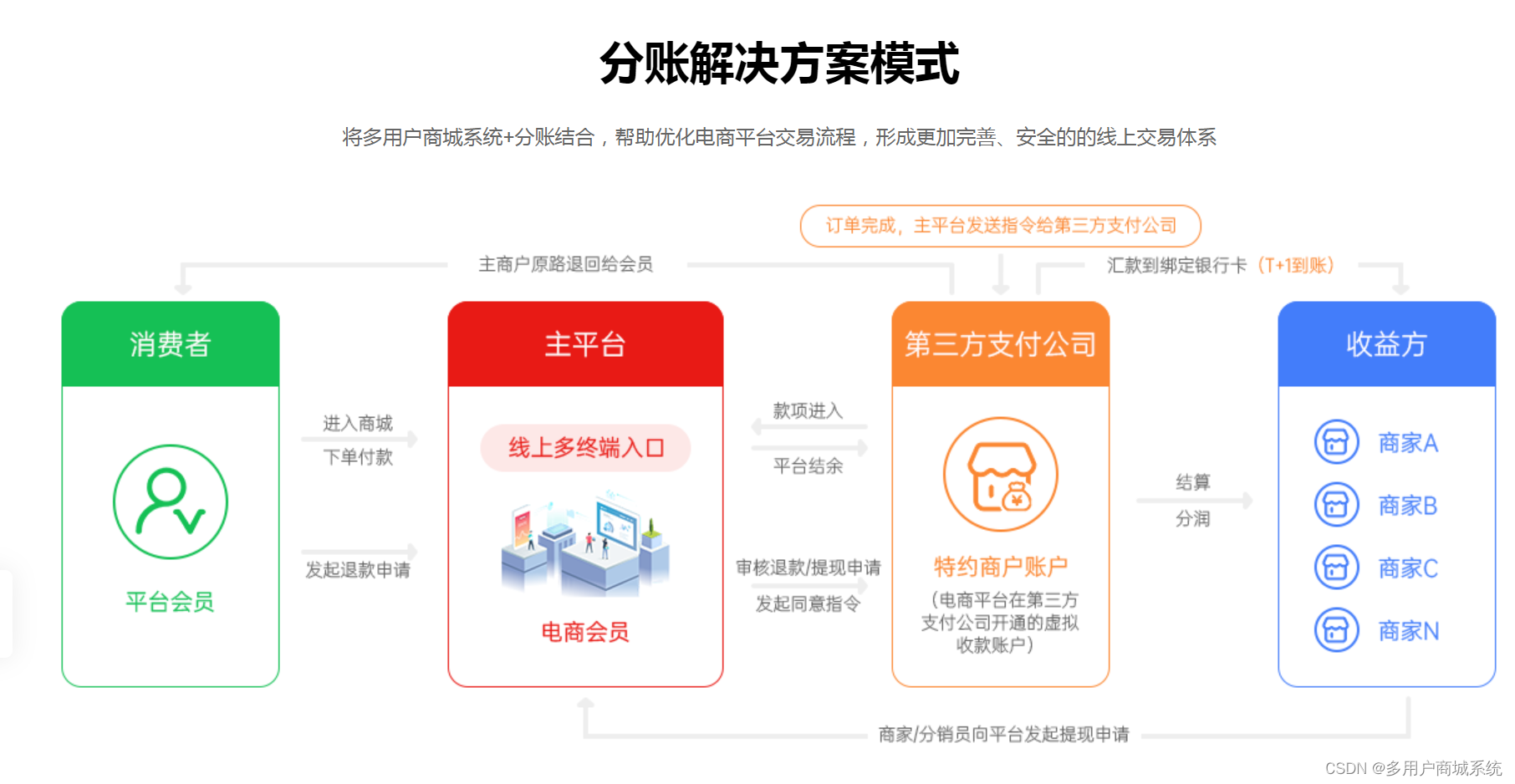
小程序分账方案:实现商户分账的简便与灵活
随着移动支付的普及和小程序的快速发展,越来越多的商家选择在微信小程序上开展业务。然而,对于一些有多个分账方的商户而言,如何实现快速、准确和灵活的资金分账成为了一个挑战。本文将介绍一种高效的小程序分账方案,帮助商户轻松…...

Python数值微积分,摆脱被高数支配的恐惧
文章目录 差分和累加积分多重积分 Python科学计算:数组💯数据生成 差分和累加 微积分是现代科学最基础的数学工具,但其应用对象往往是连续函数,而其在非连续函数的类比,便是差分与累加。在【numpy】中,可…...
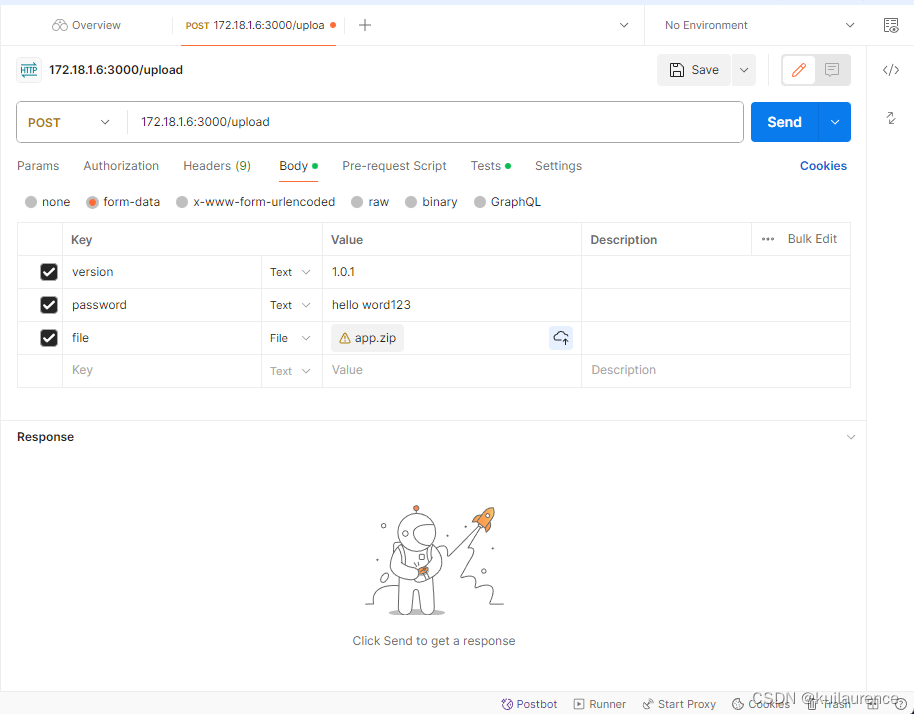
使用express+nginx+pm2+postman实现推送zip包自动更新前端网页
1.nginx配置将80端口代理到项目的3000端口 server {listen 80; #监听的端口server_name localhost; #监听的域名#charset koi8-r;#access_log logs/host.access.log main;location / {#root html;#index index.html index.html;proxy_pass http://127.0.0.1:3000; #转…...

如何在小程序中绑定身份证
在小程序中绑定身份证信息是一项常见的需求,特别是在需要进行实名认证或者身份验证的场景下。通过绑定身份证信息,可以提高用户身份的真实性和安全性,同时也为小程序提供了更多的个性化服务和功能。下面就介绍一下怎么在小程序中绑定居民身份…...
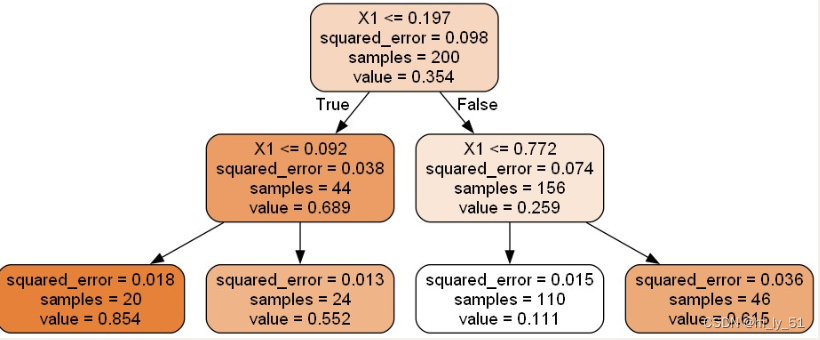
【机器学习】【决策树】分类树|回归树学习笔记总结
决策树算法概述 基本概念 决策树:从根节点开始一步步走到叶子节点,每一步都是决策过程 对于判断的先后顺序把控特别严格 一旦将判断顺序进行变化则最终的结果将可能发生改变 往往将分类效果较佳的判断条件放在前面,即先初略分在进行细节分…...
之docker搭建mysql主从集群(Replication)))
运维随录实战(14)之docker搭建mysql主从集群(Replication))
1, 从官方景镜像中拉取mysql镜像: docker pull mysql:8.0.24 --platform linux/x86_64 2, 创建master和slave容器: 在创建之前先设置网段 docker network create --subnet=172.20.0.0/24 soil_network master: docker run -d -p 3306:3306 --name mysql-master --net soi…...
CI/CD笔记.Gitlab系列:2024更新后-设置GitLab导入源
CI/CD笔记.Gitlab系列 设置GitLab导入源 - 文章信息 - Author: 李俊才 (jcLee95) Visit me at CSDN: https://jclee95.blog.csdn.netMy WebSite:http://thispage.tech/Email: 291148484163.com. Shenzhen ChinaAddress of this article:https://blog.csdn.net/qq_…...
一款Mac系统NTFS磁盘读写软件Tuxera NTFS 2023 for Mac
当您获得一台新 Mac 时,它只能读取 Windows NTFS 格式的 USB 驱动器。要将文件添加、保存或写入您的 Mac,您需要一个附加的 NTFS 驱动程序。Tuxera 的 Microsoft NTFS for Mac 2023是一款易于使用的软件,可以在 Mac 上打开、编辑、复制、移动…...
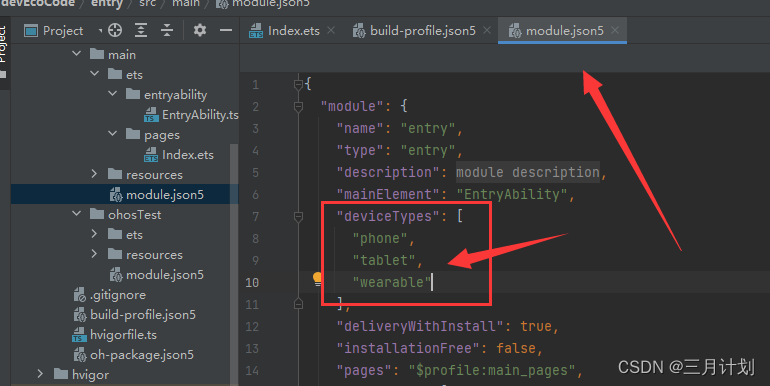
Error while Deploying HAP
第一个程序就遇到这么恶心的bug,也查了很多类似的问题是什么情况,后来无意中菜解决了这个bug,确实也是devicps下面加一个参数,但是找了半天 这是我遇到这个问题的解决办法。其他解决办法如下: https://blog.51cto.com…...

多线程扩展:乐观锁、多线程练习
悲观锁、乐观锁 悲观锁:一上来就加锁,没有安全感,每次只能一个线程进入访问完毕后,再解锁。线程安全,性能较差。 乐观锁:一开始不上锁,认为是没有问题的,等要出现线程安全问题的时…...

代码随想录day31 Java版
今天开始刷动态规划,先拿简单题练手 509. 斐波那契数 class Solution {public int fib(int n) {if (n < 1) return n; int[] dp new int[n 1];dp[0] 0;dp[1] 1;for (int index 2; index < n; index){dp[index] dp[index - 1] dp[index -…...
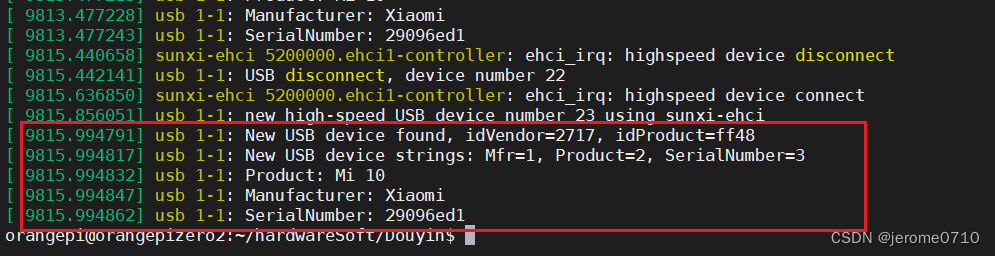
linux系统adb调试工具
adb的全称为Android Debug Bridge,就是起到调试桥的作用。通过adb可以在Eclipse中通过DDMS来调试Android程序,说白了就是调试工具。 adb的工作方式比较特殊,采用监听Socket TCP 5554等端口的方式让IDE和Qemu通讯,默认情况下adb会…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...
