Python数值微积分,摆脱被高数支配的恐惧
文章目录
- 差分和累加
- 积分
- 多重积分
Python科学计算:数组💯数据生成
差分和累加
微积分是现代科学最基础的数学工具,但其应用对象往往是连续函数,而其在非连续函数的类比,便是差分与累加。在【numpy】中,可通过【diff】和【cumsum】来完成这两项任务。
以 y = sin 2 x y=\sin 2x y=sin2x为例,其导数为 d y d x = 2 cos x \frac{\text dy}{\text dx}=2\cos x dxdy=2cosx,积分则为 ∫ y d x = − 1 2 cos 2 x + C \int y\text dx=-\frac{1}{2}\cos 2x+C ∫ydx=−21cos2x+C, C C C是某个常数。这三个函数的曲线分别为

绘图函数如下
import matplotlib.pyplot as plt
import numpy as np
dx = 0.1
x = np.arange(100)*dx
y = np.sin(2*x)
plt.plot(x, y, label="y=sin(2x)")
plt.plot(x[1:], np.diff(y)/dx, label="diff(y)/dx")
plt.plot(x, np.cumsum(y)*dx, label="cumsum(y)*dx")plt.grid()
plt.legend()
plt.show()
其中,diff用于求差分,其输入参数除了待差分数组之外,还有n和axis,比较常用,n为差分的阶数,默认为1;axis用于高维数组中,表示计算的方向,默认-1表示最后一个轴。
cumsum用于累加,对于输入数组 y y y,其返回数组为 S S S,则 S n = ∑ i = 0 n y i S_n=\sum_{i=0}^ny_i Sn=∑i=0nyi。
无论diff还是cumsum,均只针对输入数组进行操作,而不会考虑微积分中至关重要的 d x \text dx dx,所以绘图时对这一部分进行了补全。
此外,由于差分的实质是后一个减去前一个,所以元素个数必然会减少,所以在绘图时,令 x x x从1开始。这是一个在编程时很容易出错的地方,故而numpy还提供了另一个函数【ediff1d】,这是一个只做一阶差分计算的函数,但提供了to_end和to_begin参数,分别用于在diff计算结果的后面或前面补充数值。
积分
积分一开始被引入教材,是以梯形求和为示例的:将函数 y = f ( x ) y=f(x) y=f(x)无限分割,然后对相邻两点取平均,再乘以 d x \text dx dx之后进行求和,即 lim δ x → 0 ∑ y i + y i + 1 2 δ x \lim_{\delta_x\to0}\sum \frac{y_{i}+y_{i+1}}{2}\delta_x limδx→0∑2yi+yi+1δx。
【trapz】可实现上述过程,但要求 y y y是一个给定的数组,且 δ x \delta_x δx为1。很显然,这个过程只能称之为梯形求和,毕竟积分的要求是 δ x → 0 \delta_x\to0 δx→0, 1 1 1和 0 0 0有着本质的区别。
为此,【scipy.intergrate】作为顾名思义的积分模块,提供了真真正正的积分。为了行文简洁,后文将此模块简称为【si】模块。
【quad】是【si】中最常用的积分函数,以函数 x 2 x^2 x2和 sin x \sin x sinx为例,其使用流程如下
import numpy as np
from scipy.integrate import quadfunc = lambda x: x**2
quad(func, 0, 4) # (21.33, 2.37-13)
quad(np.sin, 0, np.pi) # (2.0, 2.22e-14)
其中,quad共输入了三个参数,分别是待积分函数、积分下界与积分上界,其返回值有二,分别为积分结果和计算误差。
这两个测试函数的解析形式如下,可见计算结果基本温和。
∫ 0 4 x 2 d x = 1 3 x 3 ∣ 0 4 = 64 3 ≈ 21.3 ∫ 0 π sin x d x = − cos x ∣ 0 π = 2 \int_0^4 x^2\text dx=\frac{1}{3}x^3\big|^4_0=\frac{64}{3}\approx 21.3\\ \int^\pi_0\sin x\text dx=-\cos x\big|^\pi_0=2 ∫04x2dx=31x3 04=364≈21.3∫0πsinxdx=−cosx 0π=2
除了三个必须输入的参数之外,下列参数也较为常用
args为func函数中,除待求积分参数之外的其他参数,默认为空epsabs, epsrel分别为绝对和相对误差,默认为 1.49 × 1 0 − 8 1.49\times10^{-8} 1.49×10−8limit自适应算法中子区间的个数,默认50points断点位置,默认为Noneweight, wvar定义域区间内的权重类型和权重,默认为Nonewopts, maxp1切比雪夫矩及其上限,默认为None和50- full_output=0, limlst=50, complex_func=False
其中,weight和wvar参数的具体取值如下。
| weight | wvar | 函数 |
|---|---|---|
| “cos” | w w w | cos w x \cos wx coswx |
| “sin” | w w w | sin w x \sin wx sinwx |
| “alg” | α , β \alpha, \beta α,β | g ( x ) g(x) g(x) |
| “alg-loga” | α , β \alpha, \beta α,β | g ( x ) log ( x − a ) g(x)\log(x-a) g(x)log(x−a) |
| “alg-logb” | α , β \alpha, \beta α,β | g ( x ) log ( b − x ) g(x)\log(b-x) g(x)log(b−x) |
| “alg-log” | α , β \alpha, \beta α,β | g ( x ) log ( x − a ) log ( b − x ) g(x)\log(x-a)\log(b-x) g(x)log(x−a)log(b−x) |
| “cauchy” | c c c | 1 x − c \frac{1}{x-c} x−c1 |
其中, g ( x ) = ( x − a ) α ∗ ( b − x ) β g(x)=(x-a)^\alpha*(b-x)^\beta g(x)=(x−a)α∗(b−x)β
设func为 f ( x ) = x f(x)=x f(x)=x,若weight参数为cos,而wvar取值为 w w w,则实际计算的积分表达式为
∫ a b cos w f ( x ) d x \int_a^b\cos wf(x)\text dx ∫abcoswf(x)dx
示例如下
func = lambda x : x
quad(func, 0, np.pi) # (4.935, 5.478e-14)
quad(func, 0, np.pi, weight='cos', wvar=1) # (-2.00, 1.926e-13)
多重积分
在【si】中,除了quad之外,还提供了二重、三重以及N重积分的API,分别是【dblquad, tplquad, nquad】,三者所需参数如下
MIN = 1.49e-08
dblquad(func, a, b, gfun, hfun, args=(), epsabs=MIN, epsrel=MIN)
tplquad(func, a, b, gfun, hfun, qfun, rfun, args=(), epsabs=MIN, epsrel=MIN)
nquad(func, ranges, args=None, opts=None, full_output=False)
dblquad
以二重积分为例,其对应的问题可表述为下式
∫ a b ∫ y g ( x ) y h ( x ) f ( y , x ) d x d y \int^b_a\int^{y_h(x)}_{y_g(x)} f(y,x)\text dx\text dy ∫ab∫yg(x)yh(x)f(y,x)dxdy
在函数dblquad中,func对应 f ( y , x ) f(y,x) f(y,x),a,b对那个上式的 a , b a,b a,b,gfun, hfun对应上式的 y g ( x ) , y h ( x ) y_g(x), y_h(x) yg(x),yh(x)。
接下来求解下面的积分
∫ 1 2 ∫ x 2 x 3 x y d y d x = ∫ 1 2 1 2 ( x y 2 ) ∣ x 2 x 3 d x = ∫ 1 2 1 2 ( x 7 − x 5 ) d x = 1 2 ( 1 8 x 8 − 1 6 x 6 ) ∣ 1 2 = 1 2 ( 2 8 8 − 2 6 6 ) + 1 48 = 513 48 \begin{aligned} &\int^2_1\int^{x^3}_{x^2} xy\text dy\text dx\\ =&\int^2_1 \frac{1}{2}(xy^2)\vert^{x^3}_{x^2}\text dx=&\int^2_1 \frac{1}{2}(x^7-x^5)\text dx\\ =&\frac1 2(\frac1 8x^8-\frac1 6x^6)\vert^2_1=&\frac1 2(\frac{2^8}{8}-\frac{2^6}{6})+\frac{1}{48}\\ =&\frac{513}{48} \end{aligned} ===∫12∫x2x3xydydx∫1221(xy2)∣x2x3dx=21(81x8−61x6)∣12=48513∫1221(x7−x5)dx21(828−626)+481
Python代码如下
from scipy.integrate import dblquad
func = lambda x,y : x*y
gf = lambda x: x**2
hf = lambda x: x**3
dblquad(func, 1, 2, gf, hf)
# (10.6875, 5.284867210146833e-13)
计算结果与 513 48 \frac{513}{48} 48513一致。
与二重积分相比,三重积分tplquad只是多了一组qfun和rfun,相当于z处于qfun(x,y)和rfun(x,y)之间。
【nquad】貌似不支持回调函数,其参数ranges是元组的列表,每个元组代表对应未知量的取值范围。若将其映射为三重积分函数,则ranges可表示为 ( ( a 1 , b 1 ) , ( a 2 , b 2 ) , ⋯ , ( a n , b n ) ) ((a_1,b_1), (a_2, b_2),\cdots,(a_n, b_n)) ((a1,b1),(a2,b2),⋯,(an,bn))
下面仍以函数func为例,用nquad得出结果
from scipy.integrate import nquad
nquad(func, [[1,2], [3, 4]])
#(0.39276170758930756, 4.91851540406507e-15)
相关文章:

Python数值微积分,摆脱被高数支配的恐惧
文章目录 差分和累加积分多重积分 Python科学计算:数组💯数据生成 差分和累加 微积分是现代科学最基础的数学工具,但其应用对象往往是连续函数,而其在非连续函数的类比,便是差分与累加。在【numpy】中,可…...
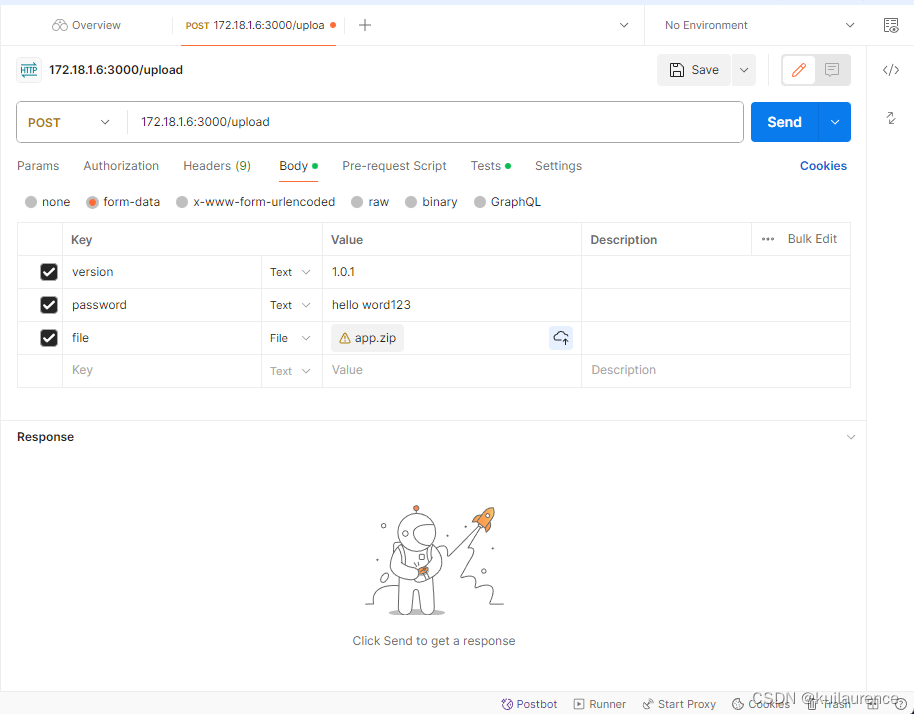
使用express+nginx+pm2+postman实现推送zip包自动更新前端网页
1.nginx配置将80端口代理到项目的3000端口 server {listen 80; #监听的端口server_name localhost; #监听的域名#charset koi8-r;#access_log logs/host.access.log main;location / {#root html;#index index.html index.html;proxy_pass http://127.0.0.1:3000; #转…...

如何在小程序中绑定身份证
在小程序中绑定身份证信息是一项常见的需求,特别是在需要进行实名认证或者身份验证的场景下。通过绑定身份证信息,可以提高用户身份的真实性和安全性,同时也为小程序提供了更多的个性化服务和功能。下面就介绍一下怎么在小程序中绑定居民身份…...
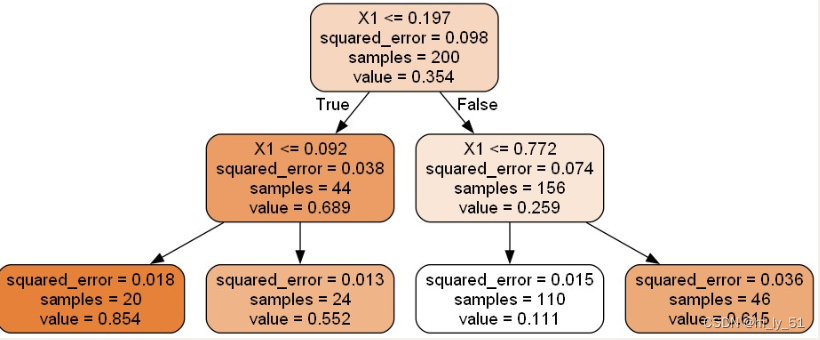
【机器学习】【决策树】分类树|回归树学习笔记总结
决策树算法概述 基本概念 决策树:从根节点开始一步步走到叶子节点,每一步都是决策过程 对于判断的先后顺序把控特别严格 一旦将判断顺序进行变化则最终的结果将可能发生改变 往往将分类效果较佳的判断条件放在前面,即先初略分在进行细节分…...
之docker搭建mysql主从集群(Replication)))
运维随录实战(14)之docker搭建mysql主从集群(Replication))
1, 从官方景镜像中拉取mysql镜像: docker pull mysql:8.0.24 --platform linux/x86_64 2, 创建master和slave容器: 在创建之前先设置网段 docker network create --subnet=172.20.0.0/24 soil_network master: docker run -d -p 3306:3306 --name mysql-master --net soi…...
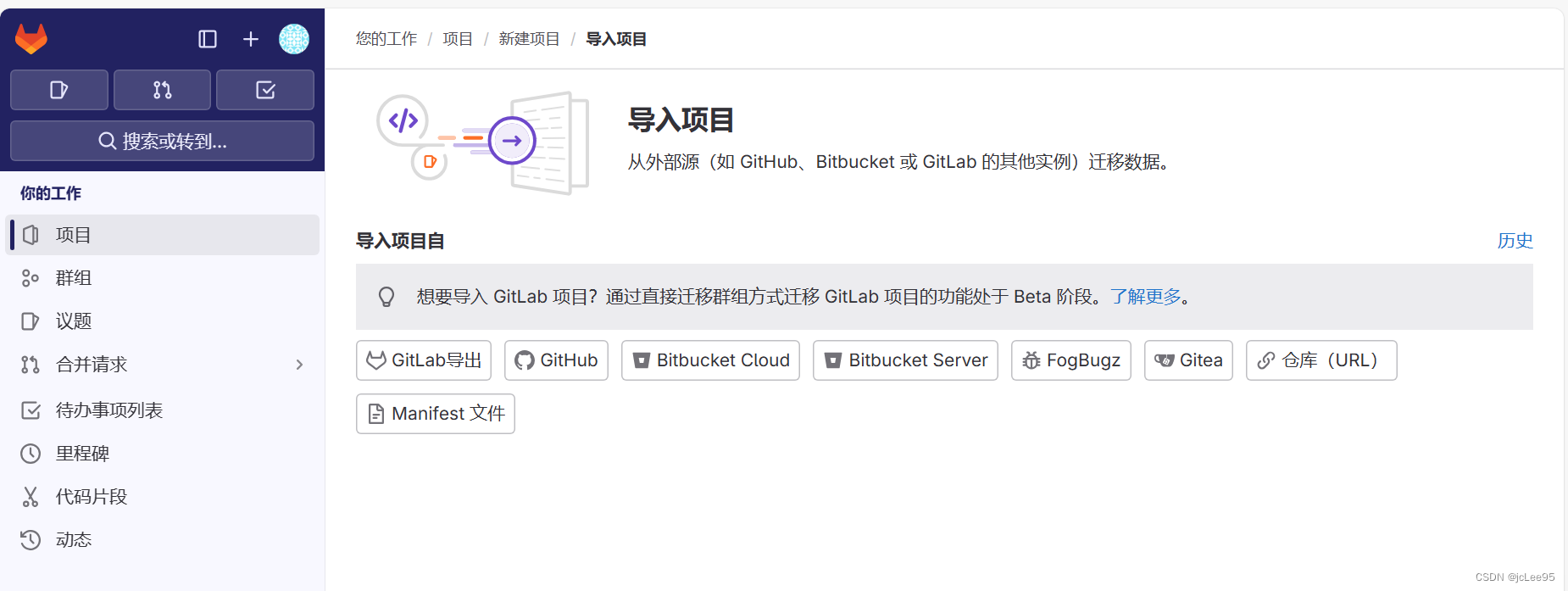
CI/CD笔记.Gitlab系列:2024更新后-设置GitLab导入源
CI/CD笔记.Gitlab系列 设置GitLab导入源 - 文章信息 - Author: 李俊才 (jcLee95) Visit me at CSDN: https://jclee95.blog.csdn.netMy WebSite:http://thispage.tech/Email: 291148484163.com. Shenzhen ChinaAddress of this article:https://blog.csdn.net/qq_…...
一款Mac系统NTFS磁盘读写软件Tuxera NTFS 2023 for Mac
当您获得一台新 Mac 时,它只能读取 Windows NTFS 格式的 USB 驱动器。要将文件添加、保存或写入您的 Mac,您需要一个附加的 NTFS 驱动程序。Tuxera 的 Microsoft NTFS for Mac 2023是一款易于使用的软件,可以在 Mac 上打开、编辑、复制、移动…...
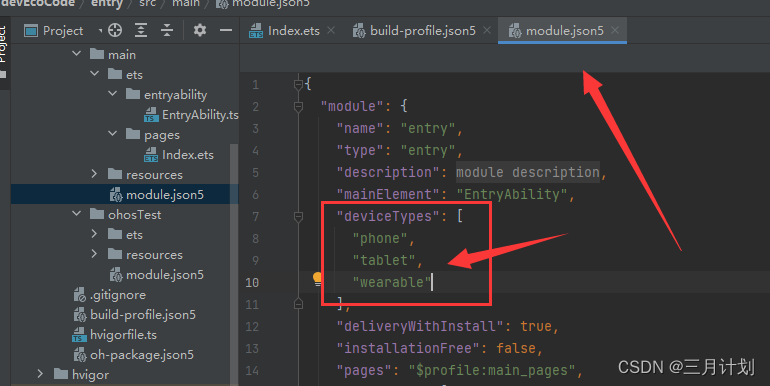
Error while Deploying HAP
第一个程序就遇到这么恶心的bug,也查了很多类似的问题是什么情况,后来无意中菜解决了这个bug,确实也是devicps下面加一个参数,但是找了半天 这是我遇到这个问题的解决办法。其他解决办法如下: https://blog.51cto.com…...

多线程扩展:乐观锁、多线程练习
悲观锁、乐观锁 悲观锁:一上来就加锁,没有安全感,每次只能一个线程进入访问完毕后,再解锁。线程安全,性能较差。 乐观锁:一开始不上锁,认为是没有问题的,等要出现线程安全问题的时…...

代码随想录day31 Java版
今天开始刷动态规划,先拿简单题练手 509. 斐波那契数 class Solution {public int fib(int n) {if (n < 1) return n; int[] dp new int[n 1];dp[0] 0;dp[1] 1;for (int index 2; index < n; index){dp[index] dp[index - 1] dp[index -…...
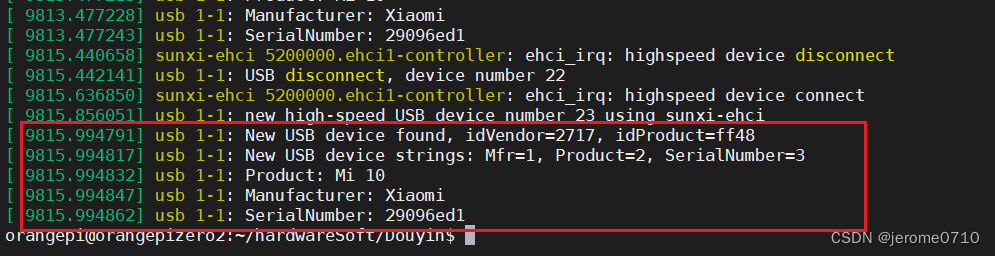
linux系统adb调试工具
adb的全称为Android Debug Bridge,就是起到调试桥的作用。通过adb可以在Eclipse中通过DDMS来调试Android程序,说白了就是调试工具。 adb的工作方式比较特殊,采用监听Socket TCP 5554等端口的方式让IDE和Qemu通讯,默认情况下adb会…...

【Golang星辰图】全面解析:Go语言在Web开发中的顶尖库和框架
创造无限可能:探索Go语言在Web开发中的强大库和框架 前言 Go语言作为一门简洁、高效的编程语言,在Web开发领域也展现出了强大的潜力。本文将会带您深入了解Go语言在Web开发中的相关库和框架,以及它们的优势和使用方法。通过学习这些内容&am…...

CSS 居中对齐 (水平居中 )
水平居中 1.文本居中对齐 内联元素(给容器添加样式) 限制条件:仅用于内联元素 display:inline 和 display: inline-block; <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8" /><…...

数据结构:图及相关算法讲解
图 1.图的基本概念2. 图的存储结构2.1邻接矩阵2.2邻接表2.3两种实现的比较 3.图的遍历3.1 图的广度优先遍历3.2 图的深度优先遍历 4.最小生成树4.1 Kruskal算法4.2 Prim算法4.3 两个算法比较 5.最短路径5.1两个抽象存储5.2单源最短路径--Dijkstra算法5.3单源最短路径--Bellman-…...
)
【c++设计模式06】创建型4:单例模式(Singleton Pattern)
【c++设计模式06】创建型4:单例模式(Singleton Pattern) 一、定义二、适用场景三、确保,一个类可以实例化一个对象四、分类1、懒汉式——首次访问时才创建实例2、饿汉式——类加载时就创建实例五、线程安全性深入讨论(懒汉式单例模式)1、懒汉式单例真的线程不安全吗?——…...

Python-OpenCV-边缘检测
摘要: 本文介绍了使用Python和OpenCV进行边缘检测的方法,涵盖了基本概念、核心组件、工作流程,以及详细的实现步骤和代码示例。同时,文章也探讨了相关的技巧与实践,并给出了常见问题与解答。通过阅读本文,…...

C#中使用 Prism 框架
C#中使用 Prism 框架 前言一、安装 Prism 框架二、模块化开发三、依赖注入四、导航五、事件聚合六、状态管理七、测试 前言 Prism 框架是一个用于构建可维护、灵活和可扩展的 XAML 应用程序的框架。它提供了一套工具和库,帮助开发者实现诸如依赖注入、模块化、导航…...
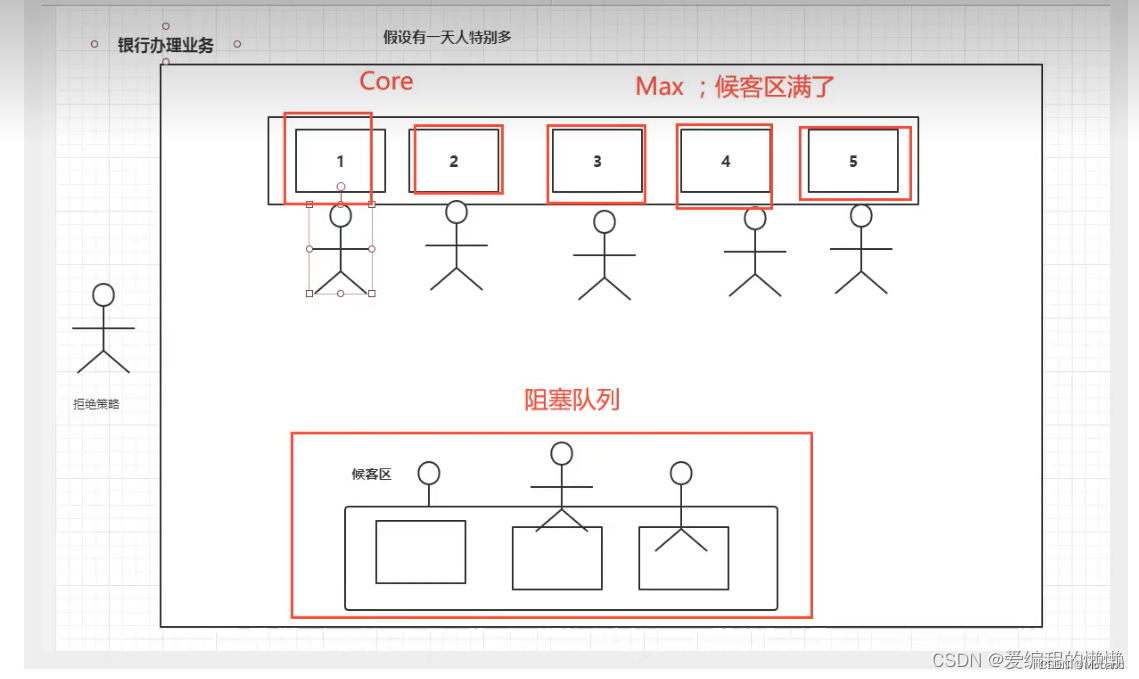
什么是线程池,线程池的概念、优点、缺点,如何使用线程池,最大线程池怎么定义?
线程池(Thread Pool)是一种并发编程中常用的技术,用于管理和重用线程。它由线程池管理器、工作队列和线程池线程组成。 线程池的基本概念是,在应用程序启动时创建一定数量的线程,并将它们保存在线程池中。当需要执行任…...
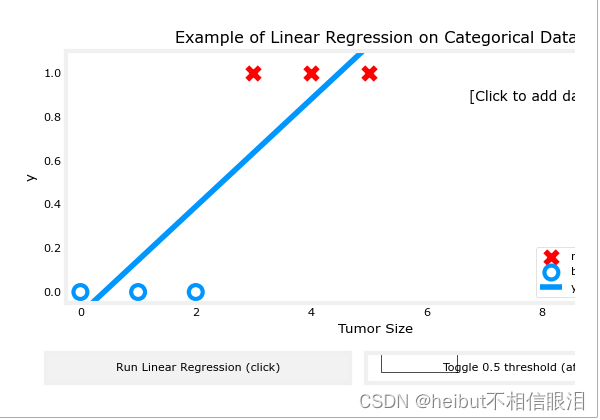
吴恩达机器学习-可选实验室:可选实验:使用逻辑回归进行分类(Classification using Logistic Regression)
在本实验中,您将对比回归和分类。 import numpy as np %matplotlib widget import matplotlib.pyplot as plt from lab_utils_common import dlc, plot_data from plt_one_addpt_onclick import plt_one_addpt_onclick plt.style.use(./deeplearning.mplstyle)jupy…...
)
序列的第 k 个数(c++题解)
题目描述 BSNY 在学等差数列和等比数列,当已知前三项时,就可以知道是等差数列还是等比数列。现在给你序列的前三项,这个序列要么是等差序列,要么是等比序列,你能求出第 m项的值吗。 如果第 项的值太大,对…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

AD学习(3)
1 PCB封装元素组成及简单的PCB封装创建 封装的组成部分: (1)PCB焊盘:表层的铜 ,top层的铜 (2)管脚序号:用来关联原理图中的管脚的序号,原理图的序号需要和PCB封装一一…...

TJCTF 2025
还以为是天津的。这个比较容易,虽然绕了点弯,可还是把CP AK了,不过我会的别人也会,还是没啥名次。记录一下吧。 Crypto bacon-bits with open(flag.txt) as f: flag f.read().strip() with open(text.txt) as t: text t.read…...

【PX4飞控】mavros gps相关话题分析,经纬度海拔获取方法,卫星数锁定状态获取方法
使用 ROS1-Noetic 和 mavros v1.20.1, 携带经纬度海拔的话题主要有三个: /mavros/global_position/raw/fix/mavros/gpsstatus/gps1/raw/mavros/global_position/global 查看 mavros 源码,来分析他们的发布过程。发现前两个话题都对应了同一…...

vxe-table vue 表格复选框多选数据,实现快捷键 Shift 批量选择功能
vxe-table vue 表格复选框多选数据,实现快捷键 Shift 批量选择功能 查看官网:https://vxetable.cn 效果 代码 通过 checkbox-config.isShift 启用批量选中,启用后按住快捷键和鼠标批量选取 <template><div><vxe-grid v-bind"gri…...

关于 ffmpeg设置摄像头报错“Could not set video options” 的解决方法
若该文为原创文章,转载请注明原文出处 本文章博客地址:https://hpzwl.blog.csdn.net/article/details/148515355 长沙红胖子Qt(长沙创微智科)博文大全:开发技术集合(包含Qt实用技术、树莓派、三维、OpenCV…...
