数据结构:图及相关算法讲解
图
- 1.图的基本概念
- 2. 图的存储结构
- 2.1邻接矩阵
- 2.2邻接表
- 2.3两种实现的比较
- 3.图的遍历
- 3.1 图的广度优先遍历
- 3.2 图的深度优先遍历
- 4.最小生成树
- 4.1 Kruskal算法
- 4.2 Prim算法
- 4.3 两个算法比较
- 5.最短路径
- 5.1两个抽象存储
- 5.2单源最短路径--Dijkstra算法
- 5.3单源最短路径--Bellman-Ford算法
- 5.4 多源最短路径--Floyd-Warshall算法
- 5.5 几个算法的比较
1.图的基本概念
概念多,但是不难理解,难的算法部分基本都是图解。
图是由顶点集合及顶点间的关系组成的一种数据结构:G = (V, E),其中V为顶点集合,E为边集合。
顶点和边:图中结点称为顶点,第i个顶点记作vi。两个顶点vi和vj相关联称作顶点vi和顶点vj之间有一条边,图中的第k条边记作ek,ek = (vi,vj)或<vi,vj>
有向图:在有向图中,顶点对<x, y>是有序的,顶点对<x,y>称为顶点x到顶点y的一条边(弧),<x, y>和<y, x>是两条不同的边,比如下图G3和G4为有向图。
无向图:顶点对(x, y)是无序的,顶点对(x,y)称为顶点x和顶点y相关联的一条边,这条边没有特定方向,(x, y)和(y,x)是同一条边,比如下图G1和G2为无向图。
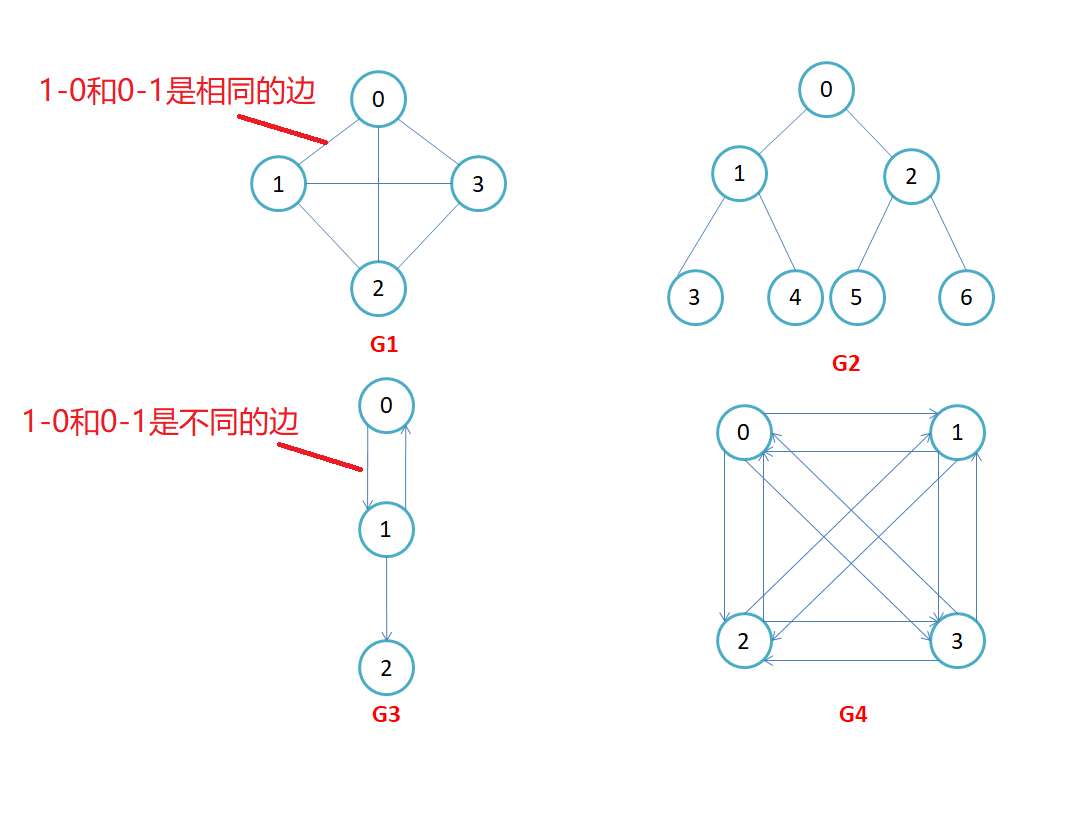
有向完全图:在有n个顶点的无向图中,若有n * (n-1)/2条边,即任意两个顶点之间有且仅有一条边,则称此图为无向完全图,比如上图G1;
无向完全图:在n个顶点的有向图中,若有n * (n-1)条边,即任意两个顶点之间有且仅有方向相反的边,则称此图为有向完全图,比如上图G4。
邻接顶点:在无向图G中,若 (u, v)是E(G)中的一条边,则称u和v互为邻接顶点,并称边(u,v)依附于顶点u和v;在有向图G中,若 <u, v>是E(G)中的一条边,则称顶点u邻接到v,顶点v邻接自顶点u,并称边<u, v>与顶点u和顶点v相关联。
顶点的度:顶点v的度是指与它相关联的边的条数,记作deg(v)。在有向图中,顶点的度等于该顶点的入度与出度之和,其中顶点v的入度是以v为终点的有向边的条数,记作indev(v);顶点v的出度是以v为起始点的有向边的条数,记作outdev(v)。因此:dev(v) = indev(v) + outdev(v)。注意:对于无向图,顶点的度等于该顶点的入度和出度,即dev(v) = indev(v) = outdev(v)。
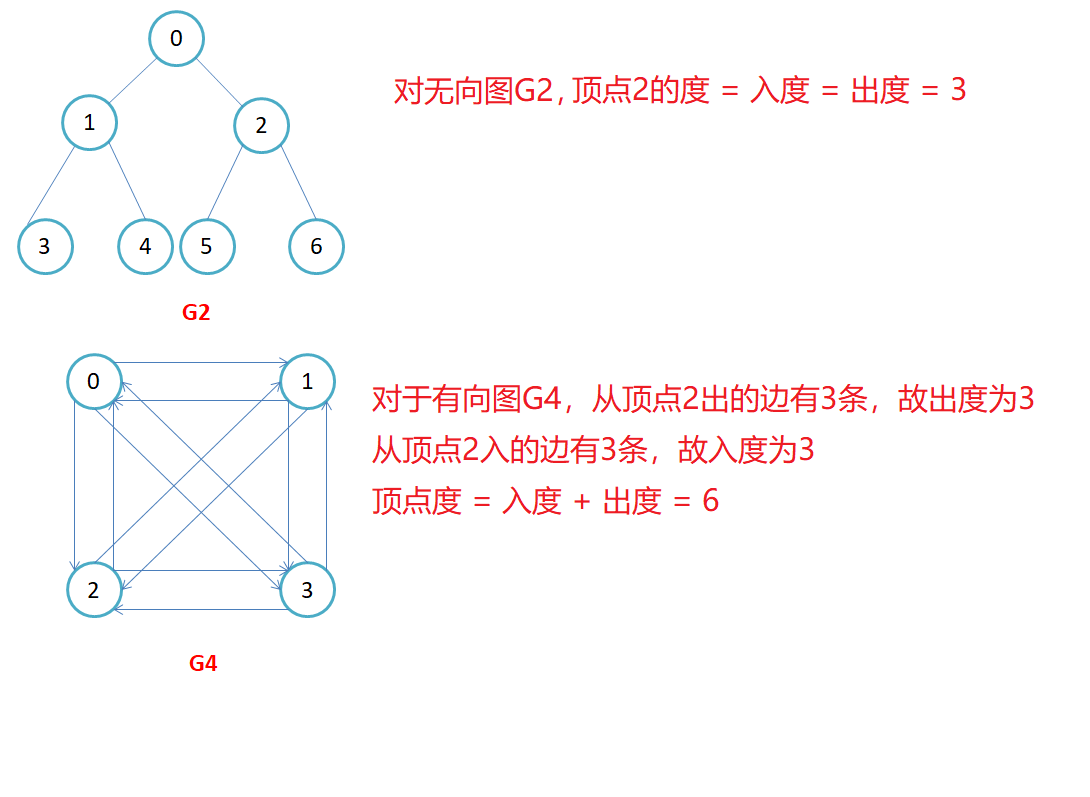
权值:边附带的数据信息。
路径:在图G = (V, E)中,若从顶点vi出发有一组边使其可到达顶点vj,则称顶点vi到顶点vj的顶点序列为从顶点vi到顶点vj的路径。
路径长度:对于不带权的图,一条路径的路径长度是指该路径上的边的条数;
对于带权的图,一条路径的路径长度是指该路径上各个边权值的总和。
简单路径与回路:若路径上各顶点v1,v2,v3,…,vm均不重复,则称这样的路径为简单路径。若路径上第一个顶点v1和最后一个顶点vm重合,则称这样的路径为回路或环。
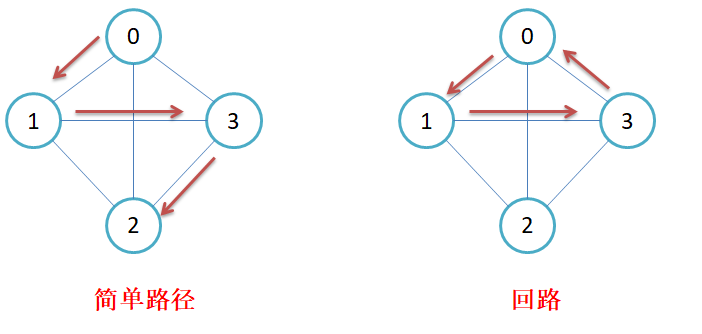
子图:设图G = {V, E}和图G1 = {V1,E1},若V1属于V且E1属于E,则称G1是G的子图。
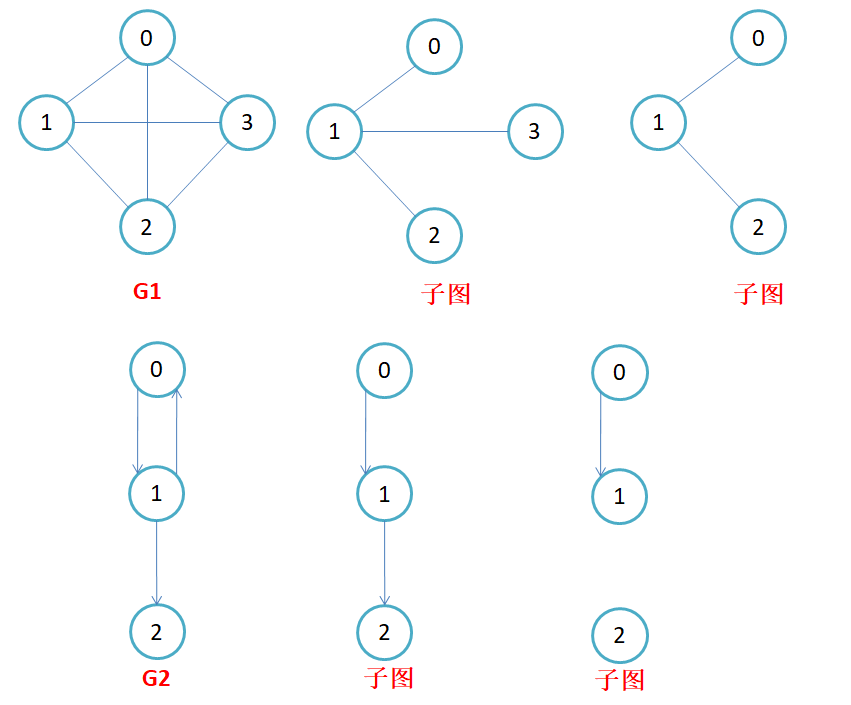
连通图:在无向图中,若从顶点v1到顶点v2有路径,则称顶点v1与顶点v2是连通的。如果图中任意一对顶点都是连通的,则称此图为连通图
强连通图:在有向图中,若在每一对顶点vi和vj之间都存在一条从vi到vj的路径,也存在一条从vj到vi的路径,则称此图是强连通图。
生成树:一个连通图的最小连通子图称作该图的生成树(形成连通图并且使用的边数量少)。有n个顶点的连通图的生成树有n个顶点和n-1条边。
图与树的关系:
- 树是一种特殊的无环连通图。
- 树关注的节点(顶点)存储的值。
- 图关注的是顶点关系以及边的权值。
2. 图的存储结构
因为图中既有节点,又有边(节点与节点之间的关系),因此,在图的存储中,只需要保存:节点和边关系即可。节点保存比较简单,只需要一段连续空间即可,那边关系该怎么保存呢?
2.1邻接矩阵
因为节点与节点之间的关系就是连通与否,即为0或者1,因此邻接矩阵(二维数组)即是:先用一个数组将定点保存,然后采用矩阵来表示节点与节点之间的关系。
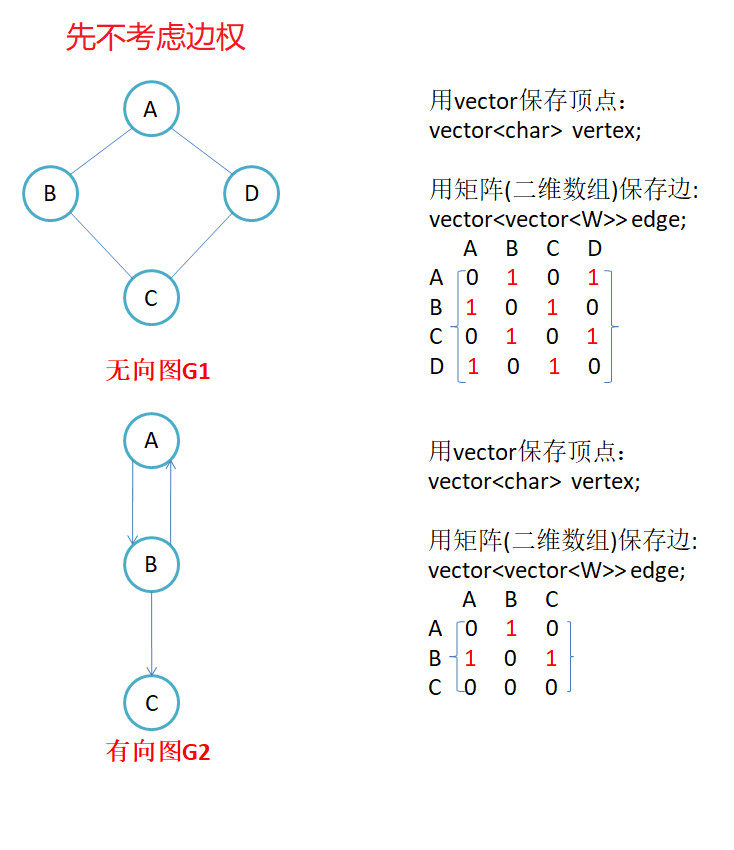
注意:
- 无向图的邻接矩阵是对称的,第i行(列)元素之和,就是顶点i的度。有向图的邻接矩阵则不一定是对称的,第i行(列)元素之后就是顶点i 的出(入)度。
- 如果边带有权值,并且两个节点之间是连通的,上图中的边的关系就用权值代替,如果两个顶点不通,则使用无穷大(自己设定值表示无穷)代替。
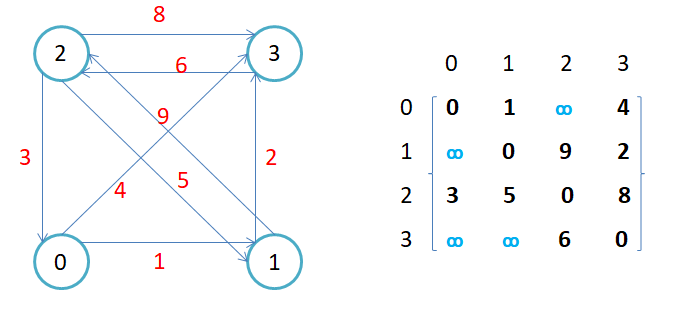
代码实现:
namespace maritx
{//V为顶点类型,无论什么类型都可以转换位对于的下标,访问时使用哈希表转换出下标//W为边类型,一般为数值类型,MAX_W代表边不存在//Direction表示方向,默认无向template<class V, class W, W MAX_W = INT_MAX, bool Direction = false> //默认无向class Graph{private:vector<V> _vertexs; //顶点map<V, size_t> _VIndexMap; //顶点 :下标vector<vector<W>> _matrix; //邻接矩阵public:typedef Graph<V, W, MAX_W, Direction> self;Graph() = default;Graph(const V* vertexs, size_t n){_vertexs.resize(n);for (size_t i = 0; i < n; i++){_vertexs[i] = vertexs[i];_VIndexMap[vertexs[i]] = i;}//初始化邻接矩阵_matrix.resize(n);for (int i = 0; i < n; i++){_matrix[i].resize(n, MAX_W);}}size_t GetVIndex(const V& v){if (_VIndexMap.count(v)){return _VIndexMap[v];}else //如果没有这个顶点{throw invalid_argument("不存在的顶点");//assert(false);return -1;}}void AddEdge(const V& src, const V& dst, const W& w){size_t srci = GetVIndex(src);size_t dsti = GetVIndex(dst);_AddEdge(srci, dsti, w);}void _AddEdge(int srci, int dsti, const W& w){_matrix[srci][dsti] = w; //有向图只需添加一边if (Direction == false){_matrix[dsti][srci] = w;}}};
}
2.2邻接表
邻接表:使用数组表示顶点的集合,使用链表表示边的关系。
-
无向图邻接表存储
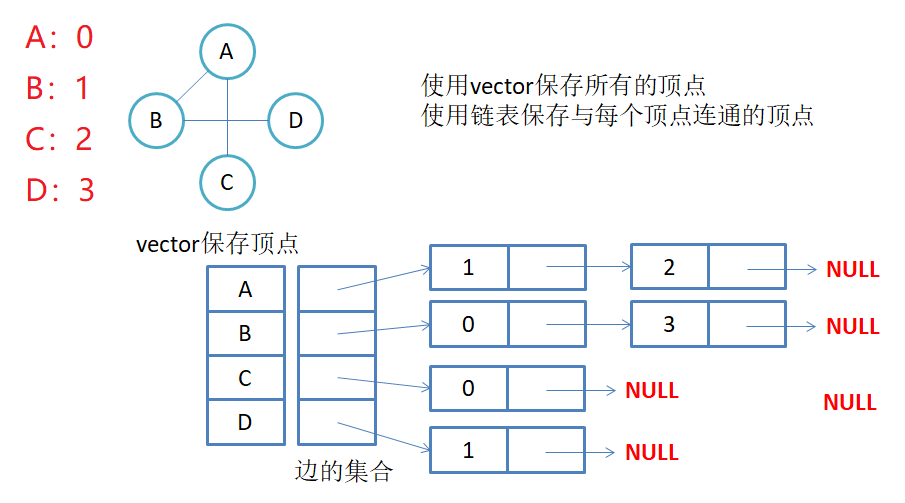
-
有向图邻接表存储
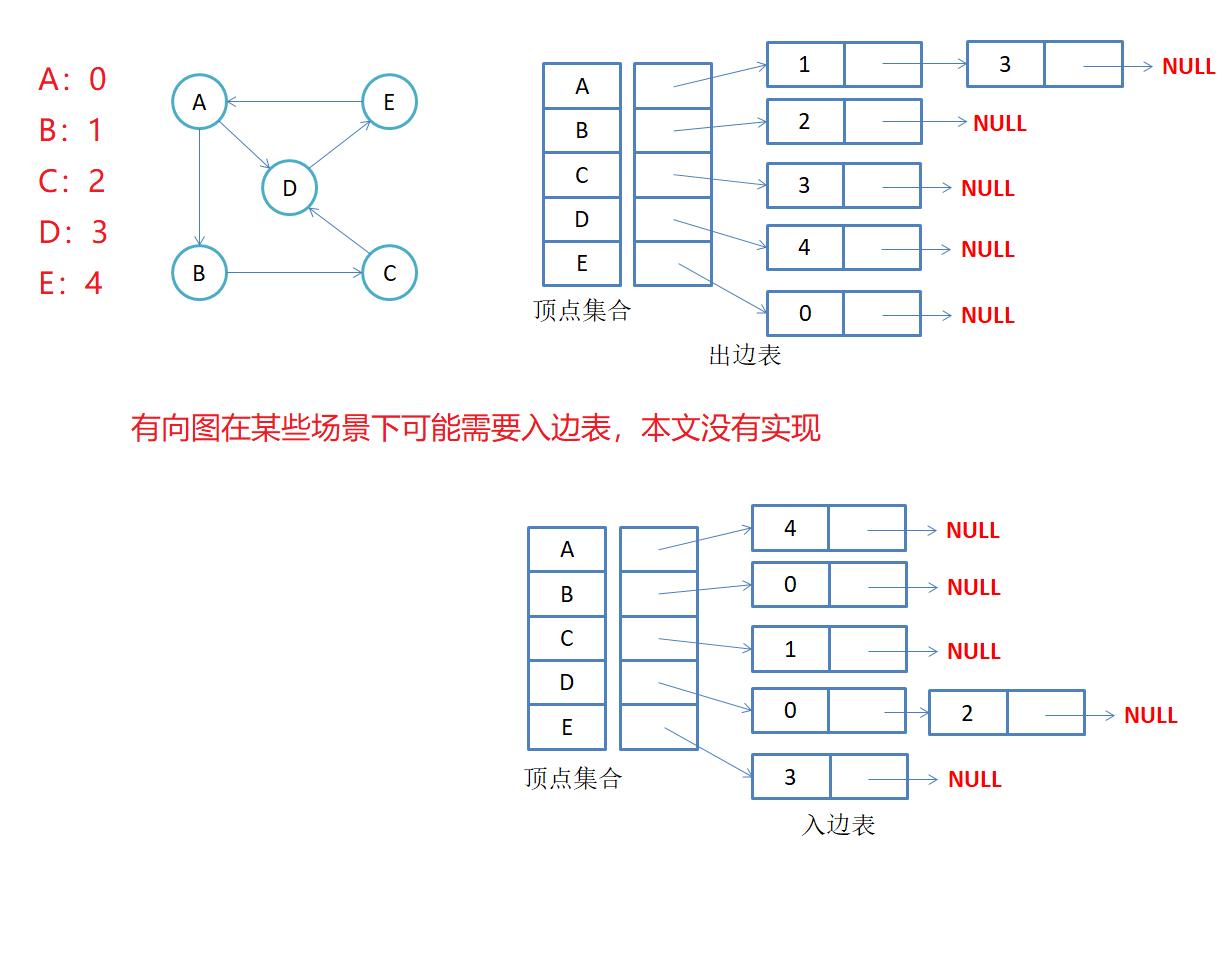
代码实现:
namespace link_table
{template<class W>struct Edge{W _w; //权值int _dsti;Edge<W>* _next;Edge(int dsti,const W& w):_dsti(dsti),_w(w),_next(nullptr){}};template<class V, class W, bool Direction = false> //默认无向class Graph{public:typedef Edge<W> Edge;Graph(const V* vertexs, size_t n){_vertexs.resize(n);for (size_t i = 0; i < n; i++){_vertexs[i] = vertexs[i];_VIndexMap[vertexs[i]] = i;}//初始化邻接矩阵_tables.resize(n, nullptr);}size_t GetVIndex(const V& v){if (_VIndexMap.count(v)){return _VIndexMap[v];}else //如果没有这个顶点{throw invalid_argument("不存在的顶点");//assert(false);return -1;}}void AddEdge(const V& src, const V& dst, const W& w){size_t srci = GetVIndex(src);size_t dsti = GetVIndex(dst);Edge* newnode = new Edge(dsti, w);newnode->_next = _tables[srci];_tables[srci] = newnode; //有向图只需添加一边if (Direction == false){Edge* newnode = new Edge(srci, w);newnode->_next = _tables[dsti];_tables[dsti] = newnode;}}void Print(){// 打印顶点和下标映射关系for (size_t i = 0; i < _vertexs.size(); ++i){cout << _vertexs[i] << "-" << i << " ";}cout << endl << endl;for (int i = 0; i < _tables.size(); i++){Edge* cur = _tables[i];if(cur) cout << i;while (cur){cout << "->" << cur->_dsti ;cur = cur->_next;}cout << endl;}}private:vector<V> _vertexs; //顶点map<V, int> _VIndexMap; //顶点:下标vector<Edge*> _tables; //邻接表};
}
2.3两种实现的比较
- 对于邻接矩阵,优点是确定AB两点间关系时方便。缺点是对于边数量少的情况,想遍历与某点的出(入)边,需要遍历矩阵的一行(N),空间也会很浪费。
- 对于邻接表,优点是边少时遍历点的出(入)边,有几条边就走几次。缺点是想确定AB两点间关系时需要遍历一次邻接表。
- 推荐关系复杂,边多时使用邻接矩阵。 关系简单,边少时使用邻接表。
- 两种存储实现图相关算法差别不大,后面的算法都是基于邻接矩阵的。
3.图的遍历
给定一个图G和其中任意一个顶点v0,从v0出发,沿着图中各边访问图中的所有顶点,且每个顶点仅被遍历一次。"遍历"即对结点进行某种操作的意思。
树的遍历是自顶点向下,图的遍历是选定一个顶点作为起点。
3.1 图的广度优先遍历
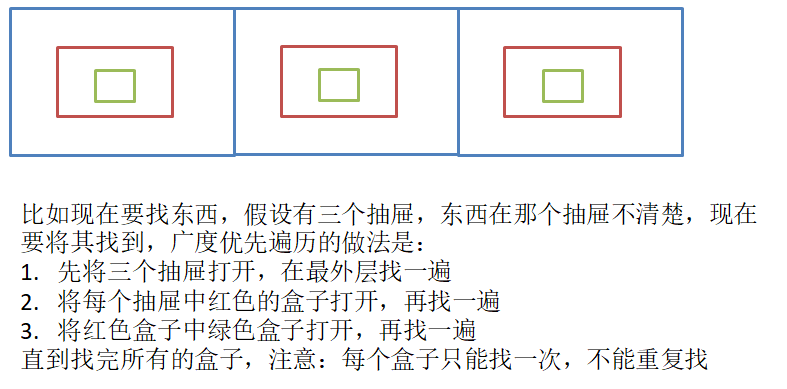
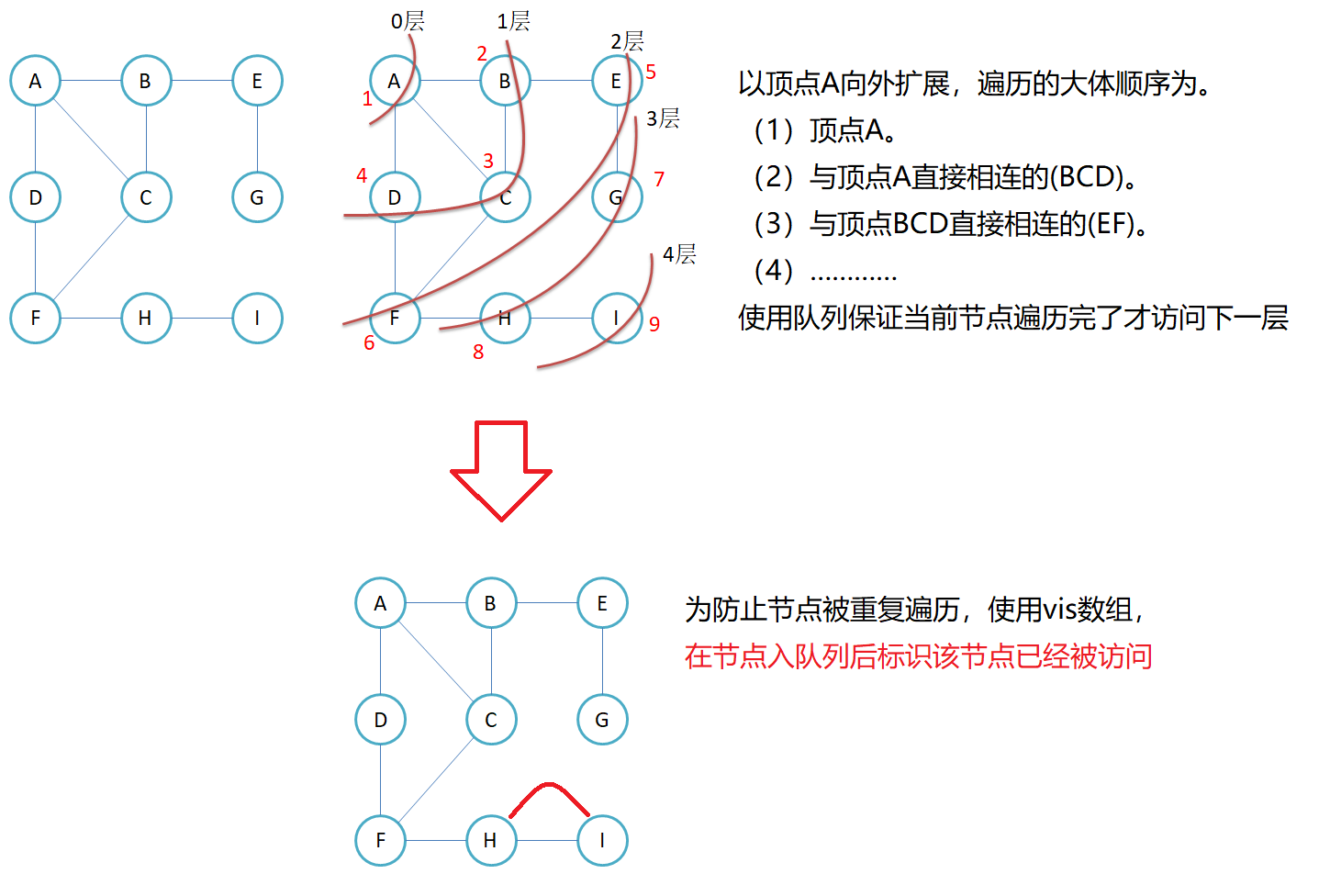
//遍历
void BFS(const V& v)
{size_t n = _vertexs.size();size_t srci = GetVIndex(v);vector<bool> visited(n);queue<size_t> q;q.push(srci);visited[srci] = true;while (!q.empty()){size_t sz = q.size();for (size_t i = 0; i < sz; i++){size_t top = q.front(); q.pop();cout << _vertexs[top] << " ";for (size_t j = 0; j < n; j++){if (_matrix[top][j] != MAX_W && visited[j] != true) //存在并且没有访问过{q.push(j);visited[j] = true;}}}}//有可能存在从v点出发到不了某些点的情况,这时可遍历vis数组for (int i = 0; i < n; i++){if (visited[i] == false){cout << _vertexs[i] << " ";}}cout << endl;
}
3.2 图的深度优先遍历
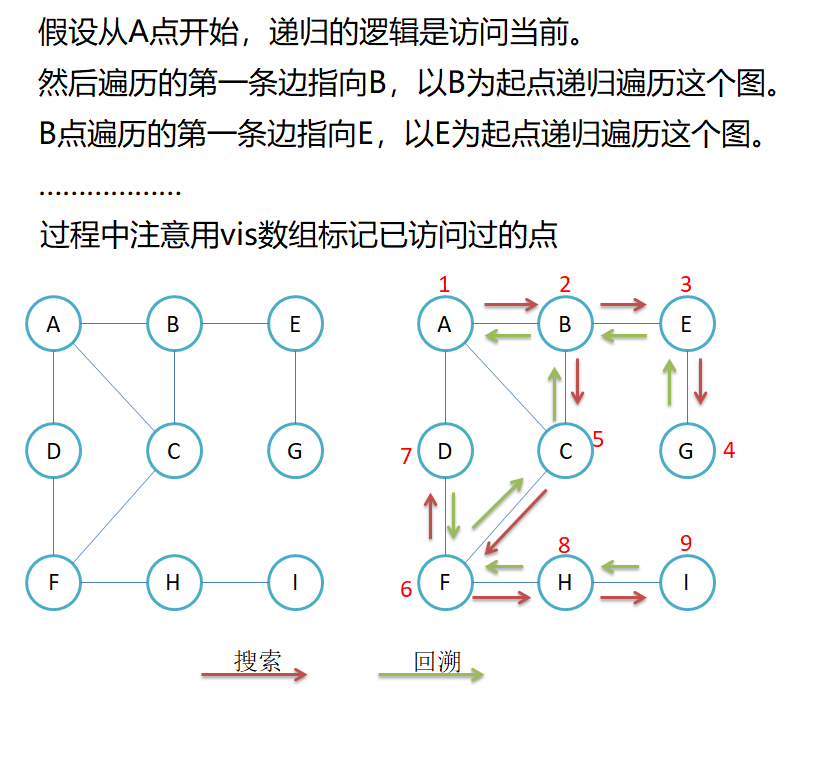
void DFS(const V& v)
{size_t srci = GetVIndex(v);vector<bool> visited(_vertexs.size());dfs(srci, visited);//有可能存在从v点出发到不了某些点的情况,这时可遍历vis数组for (int i = 0; i < n; i++){if (visited[i] == false){cout << _vertexs[i] << " ";}}
}void dfs(size_t srci, vector<bool>& visited)
{cout << _vertexs[srci] << " ";visited[srci] = true;for (int i = 0; i < _vertexs.size(); i++){if (_matrix[srci][i] != MAX_W && visited[i] != true){dfs(i, visited);}}
}
4.最小生成树
连通图中的每一棵生成树,都是原图的一个极大无环子图,即:从其中删去任何一条边,生成树就不在连通;反之,在其中引入任何一条新边,都会形成一条回路。
若连通图由n个顶点组成,则其生成树必含n个顶点和n-1条边。因此构造最小生成树的准则有三条:
- 只能使用图中的边来构造最小生成树
- 只能使用恰好n-1条边来连接图中的n个顶点
- 选用的n-1条边不能构成回路
构造最小生成树的方法:Kruskal算法和Prim算法。这两个算法都采用了逐步求解的贪心策略。
贪心算法:是指在问题求解时,总是做出当前看起来最好的选择。也就是说贪心算法做出的不是整体最优的的选择,而是某种意义上的局部最优解。贪心算法不是对所有的问题都能得到整体最优解,Kruskal算法和Prim算法都可保证最优,两种策略相当容易记忆,证明难度较大,本文不做证明。
4.1 Kruskal算法
- 每次都选用图中权值最小的边来构造,可以使用堆实现。
- 只能选n - 1条边。
- 选用的边不可构成回路,可以使用并查集来判断环是否存在。
不了解并查集的可以看这篇文章(很简单的):并查集
不了解堆的可以看这篇文章:堆
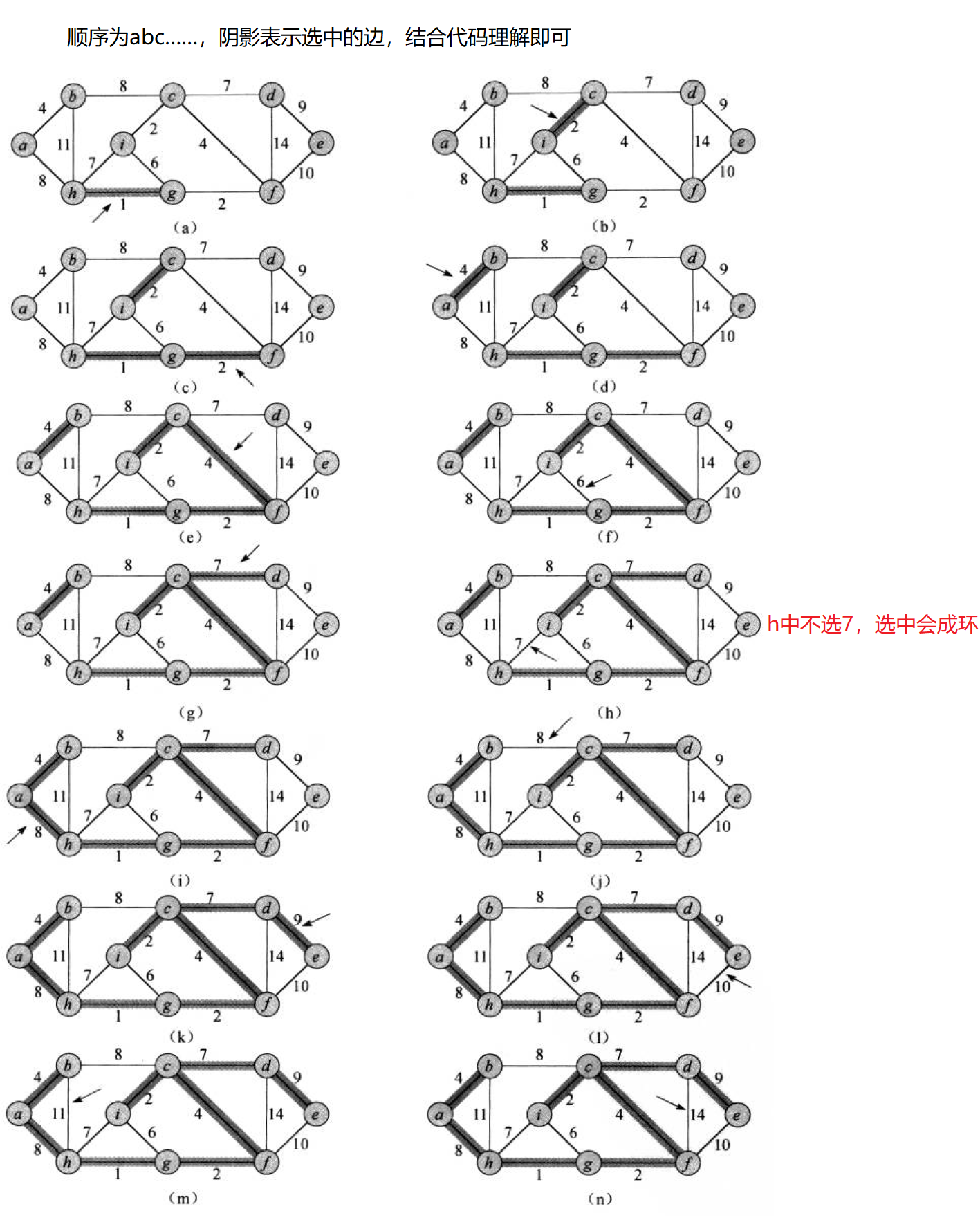
struct Edge //存储边信息
{int _srci;int _dsti;W _w;Edge(int srci, int dsti, W w):_srci(srci),_dsti(dsti),_w(w){}bool operator>(const Edge& edge) const{return _w > edge._w;}
};//Kruskal(克鲁斯卡尔),生成的了返回权值,生成不了返回W默认值
W Kruskal(self& minTree)
{//初始化一下最小生成树size_t n = _vertexs.size();minTree._vertexs = _vertexs;minTree._VIndexMap = _VIndexMap;minTree._matrix.resize(n);for (auto& e : minTree._matrix){e.resize(_vertexs.size(), MAX_W);}UnionFindSet ufs(n); //并查集priority_queue<Edge, vector<Edge>, greater<Edge>> pq; //堆//入边for (int i = 0; i < n; i++){for (int j = i; j < n; j++) //无向图只需要一半即可{if(_matrix[i][j] != MAX_W)pq.push(Edge(i, j, _matrix[i][j]));}}//依次选最小边,选n - 1size_t esum = 0;W ret = 0;//不断选最小边即可while (!pq.empty()){Edge e = pq.top(); pq.pop();if (!ufs.InSet(e._srci, e._dsti)) //不在一个集合(不构成回路),当前边可选{minTree.AddEdge(e._srci, e._dsti, e._w);esum++;ret += e._w;ufs.Union(e._srci, e._dsti);}}//判断可否形成最小生成树if (esum == n - 1){return ret;}else{return W();}
}
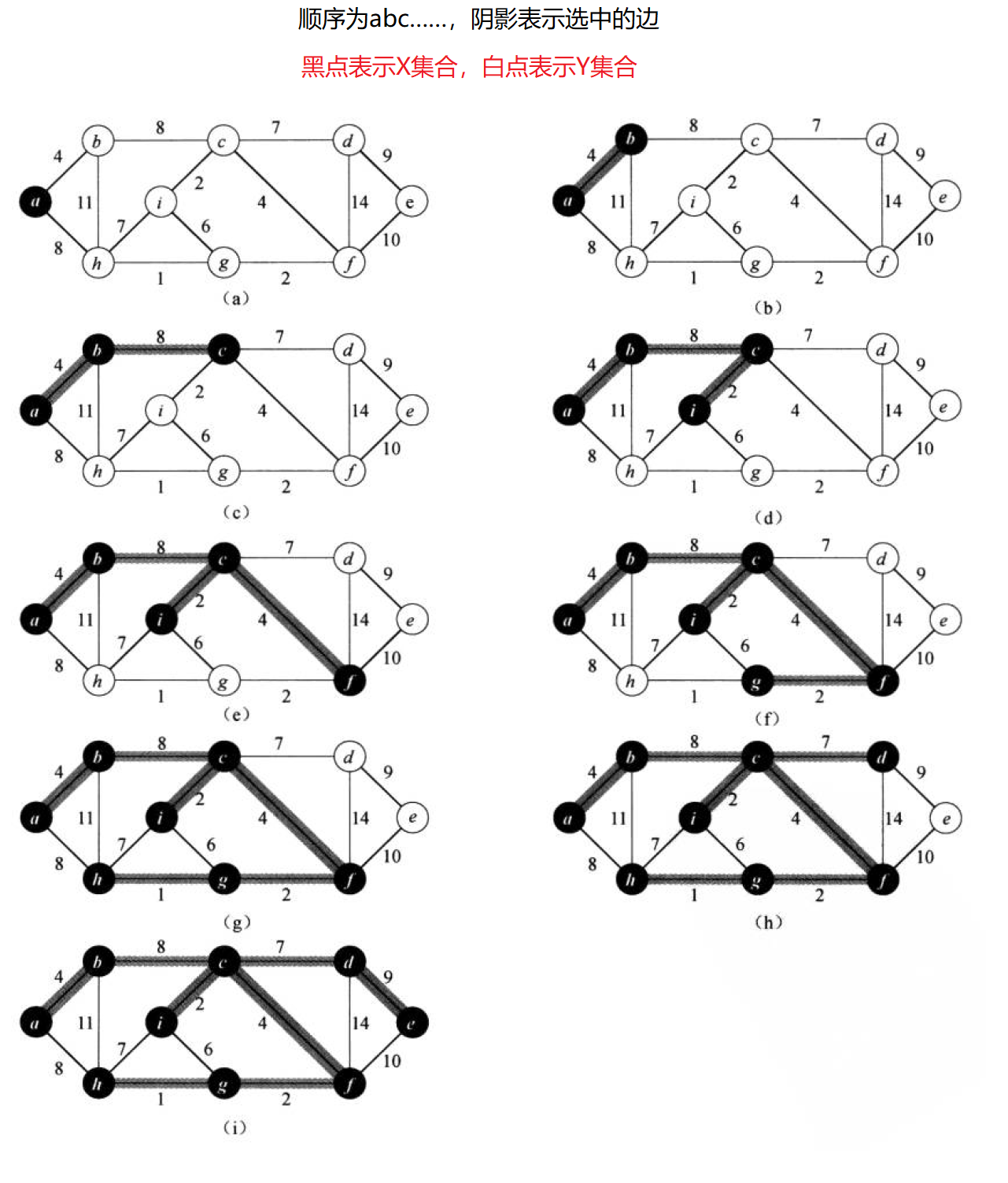
4.2 Prim算法
- Kruskal算法侧重边,Prim算法侧重点。
- 设有X,Y两个点集合,X表示已在最小生成树中的点,Y表示还未在最小生成树中的点。故选边时选的是X->Y所有边中的最小权值。
- 只能选n - 1条边。
- 选用的边不可构成回路,只需选的边起点在X,终点在Y即可。
//prim(普利姆算法)
W Prim(self& minTree, const V& src)
{//初始化一下最小生成树size_t n = _vertexs.size();minTree._vertexs = _vertexs;minTree._VIndexMap = _VIndexMap;minTree._matrix.resize(n);for (auto& e : minTree._matrix){e.resize(_vertexs.size(), MAX_W);}size_t srci = GetVIndex(src); //起点//存储边的堆priority_queue<Edge, vector<Edge>, greater<Edge>> pq;//X和Y集合(不在X就在Y)vector<bool> X(n, false);X[srci] = true;//把X初始点的边入进去for (size_t i = 0; i < n; i++){if (_matrix[srci][i] != MAX_W){pq.push(Edge(srci, i, _matrix[srci][i]));}}//选出边的条数size_t esum = 0;W ret = 0;while (!pq.empty()){Edge e = pq.top(); pq.pop();if (X[e._dsti] != true) //终点在Y,选了不成环{minTree.AddEdge(e._srci, e._dsti, e._w); esum++;ret += e._w;X[e._dsti] = true; for (int i = 0; i < n; i++){//入边为X-Y,X-X的边没必要入if (_matrix[e._dsti][i] != MAX_W && X[i] != true) {pq.push(Edge(e._dsti, i, _matrix[e._dsti][i]));}}}}//判断可否形成最小生成树if (esum == n - 1){return ret;}else{return W();}
}
4.3 两个算法比较
- Kruskal算法适用于稀疏图,即边少的图,因为该算法需要用堆维护所有的边。
- Prim算法适用于稠密图,即边多的图,因为该算法的要点在点,并不需要维护所有的边(X-X的边无需维护)。
5.最短路径
5.1两个抽象存储

基于这两个抽象数据结构还原最短路径:
//打印最短路径的算法
void PrinrtShotPath(const V& src, const vector<W>& dist, const vector<int>& pPath)
{size_t n = _vertexs.size();size_t srci = GetVIndex(src);for (size_t i = 0; i < n; i++){if (i != srci) //源到源不打印{size_t par = i;vector<size_t> path; //先从结尾开始添加while (par != srci){path.push_back(par);par = pPath[par];}path.push_back(srci); reverse(path.begin(), path.end()); //翻转过来for (auto pos : path){cout << _vertexs[pos] << "->";}cout << dist[i] << endl; //打印长度}}
}
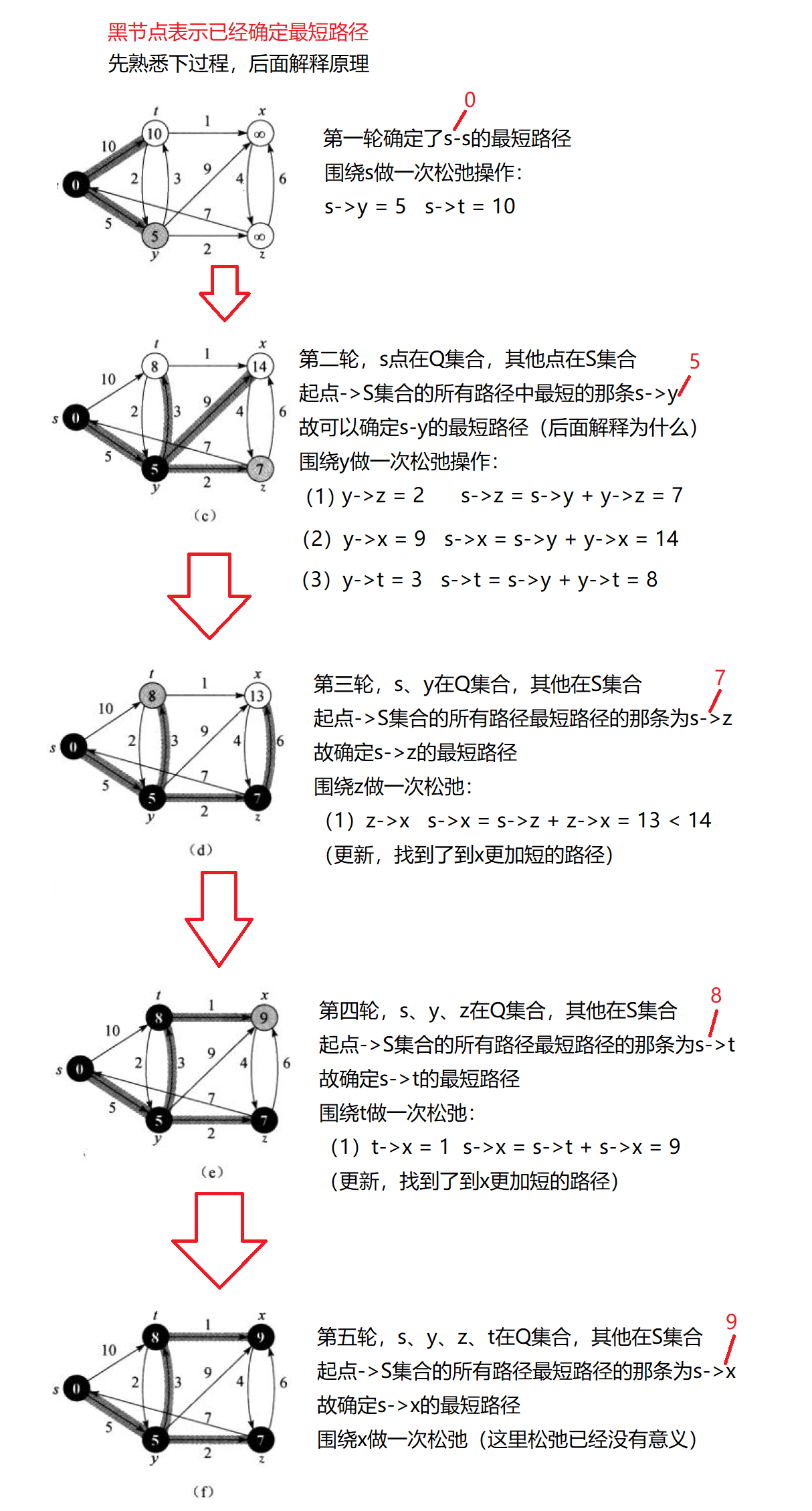
5.2单源最短路径–Dijkstra算法
- 贪心,分为两个集合Q和S,其中Q表示已经确定最短路径的顶点集合,S表示未确定最短路径的顶点集合。
- 在已有最短路径的基础上更新到其他顶点的路径,如果更短就更新,这个操作称为松弛顶点。(建议配合图解看)
- Dijkstra算法不适用于带负权的最短路径问题(后面解释)。
图解:
正确性证明:
- 图边权没有负数
(1)如果现在遍历 起点->S(未确定最短路径点集合)的边,找到一条s->x(记和为len)的最短,那就可以确定这条是s->x的最短。
(2)因为如果存在s->……(和一定小于len)->x的一条更短路径,那遍历时就会先选中s->……中的顶点进行松弛,而不是选中x进行松弛。 - 图边权有负数
(1)遍历 起点->S(未确定最短路径点集合)的边,找到一条s->x(记和为len)的最短,不能确定这条是s->x的最短。
(2)因为可能存在s->……(大于len)->负权->x(小于len),这时候就会更新不到这条真正的最短
//单源最短路径:dijkstra算法(不带负权)
//每次都可以确定一个点的最短路径,然后围绕这个点松弛
//准确性:如果当前选的不是最短,那就不会选中当前,而是其他的点,在松弛操作中更新出最短
//两个输出型参数,dist为路径长,pPath记录路径
void Dijkstra(const V& src, vector<W>& dist, vector<int>& pPath)
{size_t n = _vertexs.size();size_t srci = GetVIndex(src);//初始化dist.resize(n, MAX_W);pPath.resize(n, -1);dist[srci] = W();//Q中为true,说明已经确认最短路径vector<bool> Q(n, false);//要确定N个顶点的最短,循环N次(其实只要N-1次即可,但为了逻辑就多循环一次)for (size_t i = 0; i < n; i++){size_t u = srci;W min = MAX_W;//找到最短的路径,该路径已经可确认为最短for (size_t j = 0; j < n; j++){if (Q[j] == false && dist[j] < min){u = j;min = dist[j];}}Q[u] = true;//松弛顶点 srci-u u-v -> srci-vfor (size_t v = 0; v < n; v++){if (_matrix[u][v] != MAX_W && dist[u] + _matrix[u][v] < dist[v]){dist[v] = dist[u] + _matrix[u][v];pPath[v] = u;}} }
}
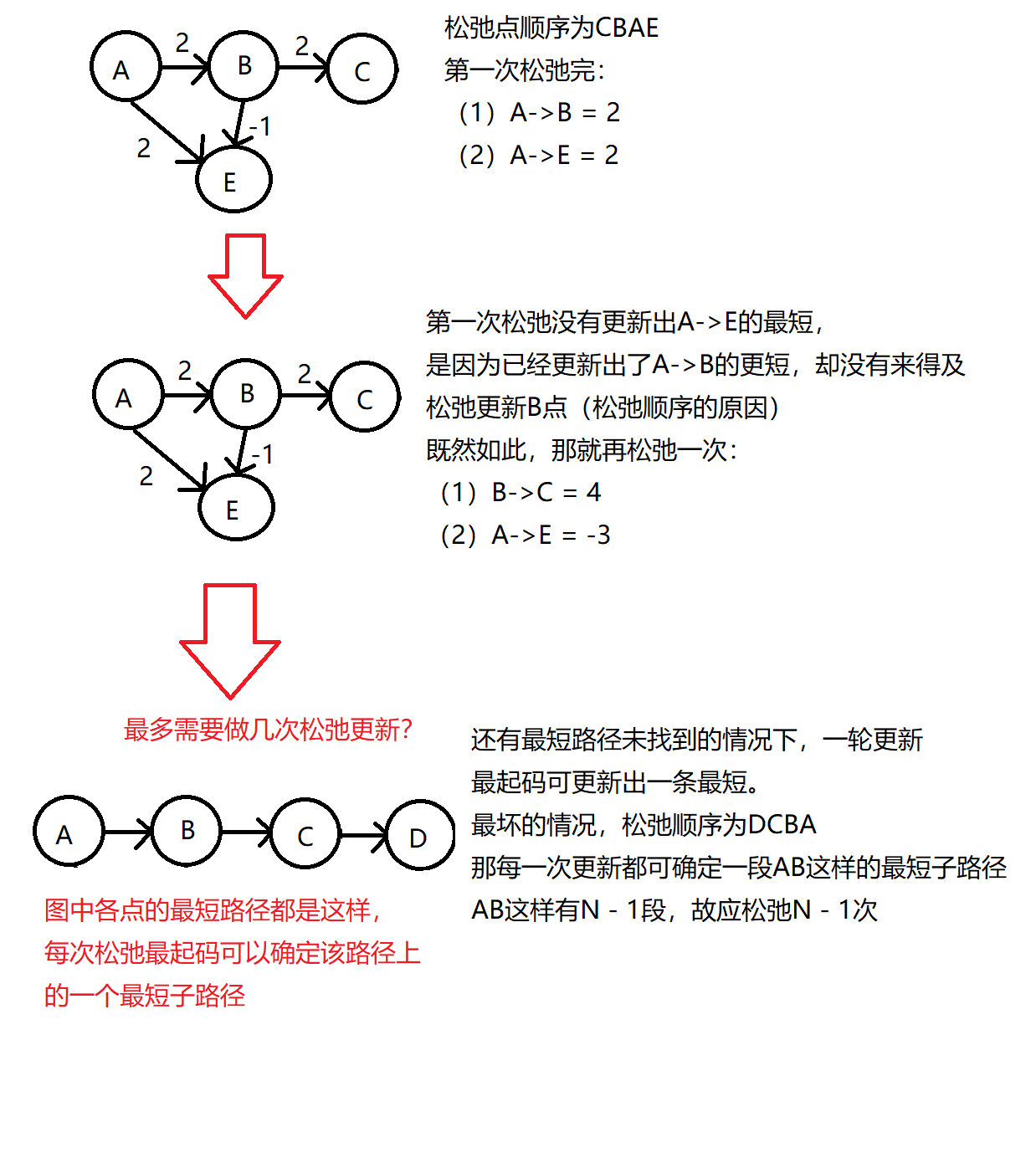
5.3单源最短路径–Bellman-Ford算法
- Bellman-Ford算法本质是暴力算法。
- Bellman-Ford算法可以解决带负权的问题。
- Bellman-Ford算法的核心在于松弛顶点。
图解:
负权回路:

//单源最短路径:BellmanFord算法(带负权,注意负权成环)
bool BellmanFord(const V& src, vector<W>& dist, vector<int>& pPath)
{size_t n = _vertexs.size();size_t srci = GetVIndex(src);//初始化dist.resize(n, MAX_W);pPath.resize(n, -1);dist[srci] = W();//最多更新n - 1for (size_t k = 0; k < n - 1; k++){//优化的标志位,如果没有松弛更短,说明所有顶点最短路径都找到了bool flag = true;//所有顶点做一次松弛for (size_t i = 0; i < n; i++){for (size_t j = 0; j < n; j++){//src - i - jif (_matrix[i][j] != MAX_W && dist[i] + _matrix[i][j] < dist[j]) //更新出更短{dist[j] = dist[i] + _matrix[i][j];pPath[j] = i;flag = false;}}}if (flag){break;}}for (size_t i = 0; i < n; i++){for (size_t j = 0; j < n; j++){//还能更新说明存在负权回路问题if (_matrix[i][j] != MAX_W && dist[i] + _matrix[i][j] < dist[j]) //更新出更短{return false;}}}return true;
}
5.4 多源最短路径–Floyd-Warshall算法
- 多源最短,即求任意两点的最短路径。
- 适用于带负权的图。
- Floyd-Warshall算法的核心是动态规划。
图解:


//多源最短路径:FloydWarshall
//vvDist和vvPPath是二维的,vvDist[x]和vvPPath[x]表示以x为起点到各点的最短路径情况
void FloydWarShall(vector<vector<W>>& vvDist, vector<vector<int>>& vvPPath)
{size_t n = _vertexs.size();vvDist.resize(n);vvPPath.resize(n);// 初始化权值和路径矩阵for (size_t i = 0; i < n; ++i){vvDist[i].resize(n, MAX_W);vvPPath[i].resize(n, -1);}//把直接相连的边入进来for (size_t i = 0; i < n; i++){for (size_t j = 0; j < n; j++){if (_matrix[i][j] != MAX_W){vvDist[i][j] = _matrix[i][j];vvPPath[i][j] = i;}//i == j,即自己到自己if (i == j){vvDist[i][j] = W();}}}//中间经过了(0, k)这些顶点for (size_t k = 0; k < n; ++k){for (size_t i = 0; i < n; i++){for (size_t j = 0; j < n; j++){if (vvDist[i][k] != MAX_W && vvDist[k][j] != MAX_W && vvDist[i][k] + vvDist[k][j] < vvDist[i][j]){vvDist[i][j] = vvDist[i][k] + vvDist[k][j];vvPPath[i][j] = vvPPath[k][j];}}}}
}
5.5 几个算法的比较
- 假设图是稠密图,我们使用矩阵存储。 对这些算法的时间复杂度分析:
Dijkstra算法:O(N ^ 2)。
Bellman-Ford算法:O(N ^ 3)。
Floyd-Warshall算法:O(N ^ 3)。 - Dijkstra算法适用于不带负权的图,如果想对不带负权的图找多源最短路径,也可以循环N次Dijkstra算法,效率和Floyd-Warshall差不多。
- Bellman-Ford算法和Floyd-Warshall算法都可以解决带负权的问题。
- Bellman-Ford算法大多数情况是快于Floyd-Warshall算法的,只是要单源最短且带负权用Bellman-Ford即可。而且针对Bellman-Ford算法可以用SPFA队列优化。(SPFA优化本文不讲,SPFA优化后时间复杂度不变,最坏的情况和朴素Bellman-Ford算法一致)
- Floyd-Warshall算法用于解决多源最短路径是效果较好,而且可解决带负权问题。
相关文章:

数据结构:图及相关算法讲解
图 1.图的基本概念2. 图的存储结构2.1邻接矩阵2.2邻接表2.3两种实现的比较 3.图的遍历3.1 图的广度优先遍历3.2 图的深度优先遍历 4.最小生成树4.1 Kruskal算法4.2 Prim算法4.3 两个算法比较 5.最短路径5.1两个抽象存储5.2单源最短路径--Dijkstra算法5.3单源最短路径--Bellman-…...
)
【c++设计模式06】创建型4:单例模式(Singleton Pattern)
【c++设计模式06】创建型4:单例模式(Singleton Pattern) 一、定义二、适用场景三、确保,一个类可以实例化一个对象四、分类1、懒汉式——首次访问时才创建实例2、饿汉式——类加载时就创建实例五、线程安全性深入讨论(懒汉式单例模式)1、懒汉式单例真的线程不安全吗?——…...

Python-OpenCV-边缘检测
摘要: 本文介绍了使用Python和OpenCV进行边缘检测的方法,涵盖了基本概念、核心组件、工作流程,以及详细的实现步骤和代码示例。同时,文章也探讨了相关的技巧与实践,并给出了常见问题与解答。通过阅读本文,…...

C#中使用 Prism 框架
C#中使用 Prism 框架 前言一、安装 Prism 框架二、模块化开发三、依赖注入四、导航五、事件聚合六、状态管理七、测试 前言 Prism 框架是一个用于构建可维护、灵活和可扩展的 XAML 应用程序的框架。它提供了一套工具和库,帮助开发者实现诸如依赖注入、模块化、导航…...
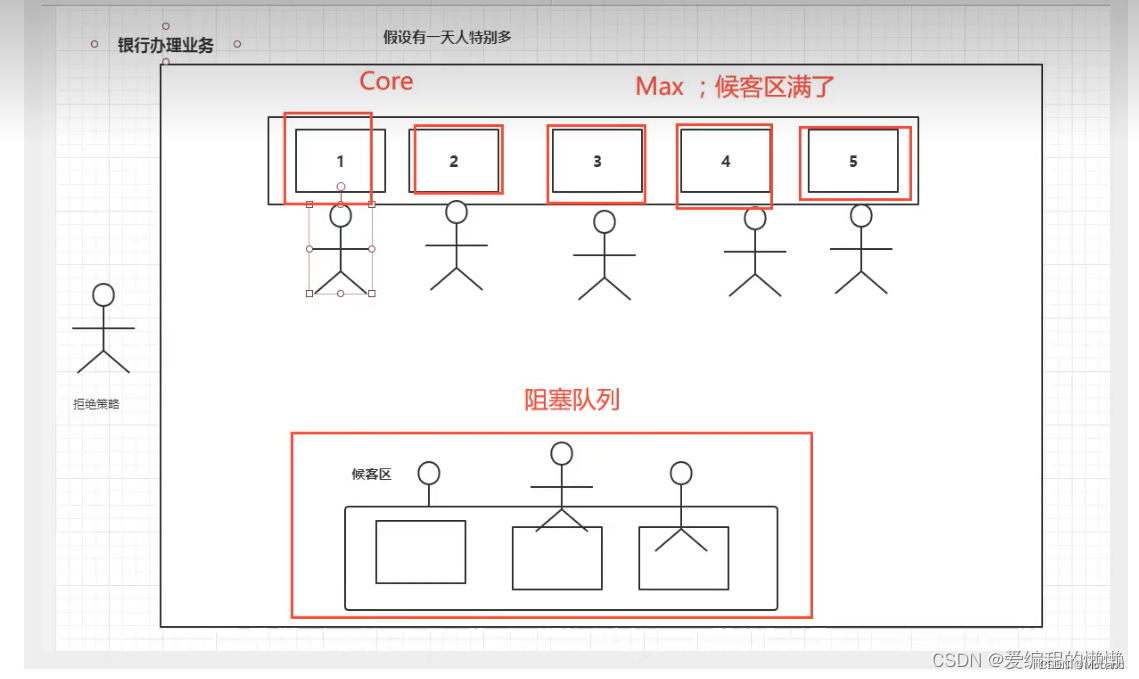
什么是线程池,线程池的概念、优点、缺点,如何使用线程池,最大线程池怎么定义?
线程池(Thread Pool)是一种并发编程中常用的技术,用于管理和重用线程。它由线程池管理器、工作队列和线程池线程组成。 线程池的基本概念是,在应用程序启动时创建一定数量的线程,并将它们保存在线程池中。当需要执行任…...
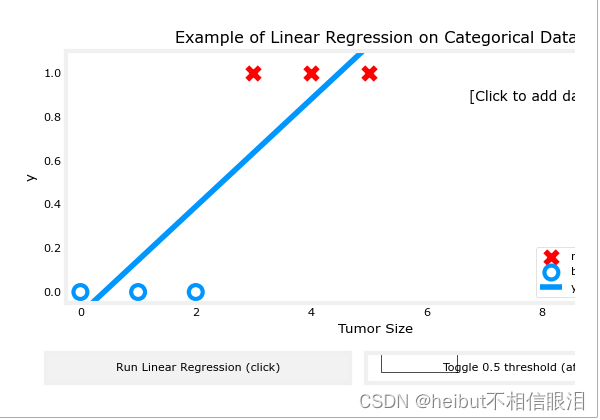
吴恩达机器学习-可选实验室:可选实验:使用逻辑回归进行分类(Classification using Logistic Regression)
在本实验中,您将对比回归和分类。 import numpy as np %matplotlib widget import matplotlib.pyplot as plt from lab_utils_common import dlc, plot_data from plt_one_addpt_onclick import plt_one_addpt_onclick plt.style.use(./deeplearning.mplstyle)jupy…...
)
序列的第 k 个数(c++题解)
题目描述 BSNY 在学等差数列和等比数列,当已知前三项时,就可以知道是等差数列还是等比数列。现在给你序列的前三项,这个序列要么是等差序列,要么是等比序列,你能求出第 m项的值吗。 如果第 项的值太大,对…...
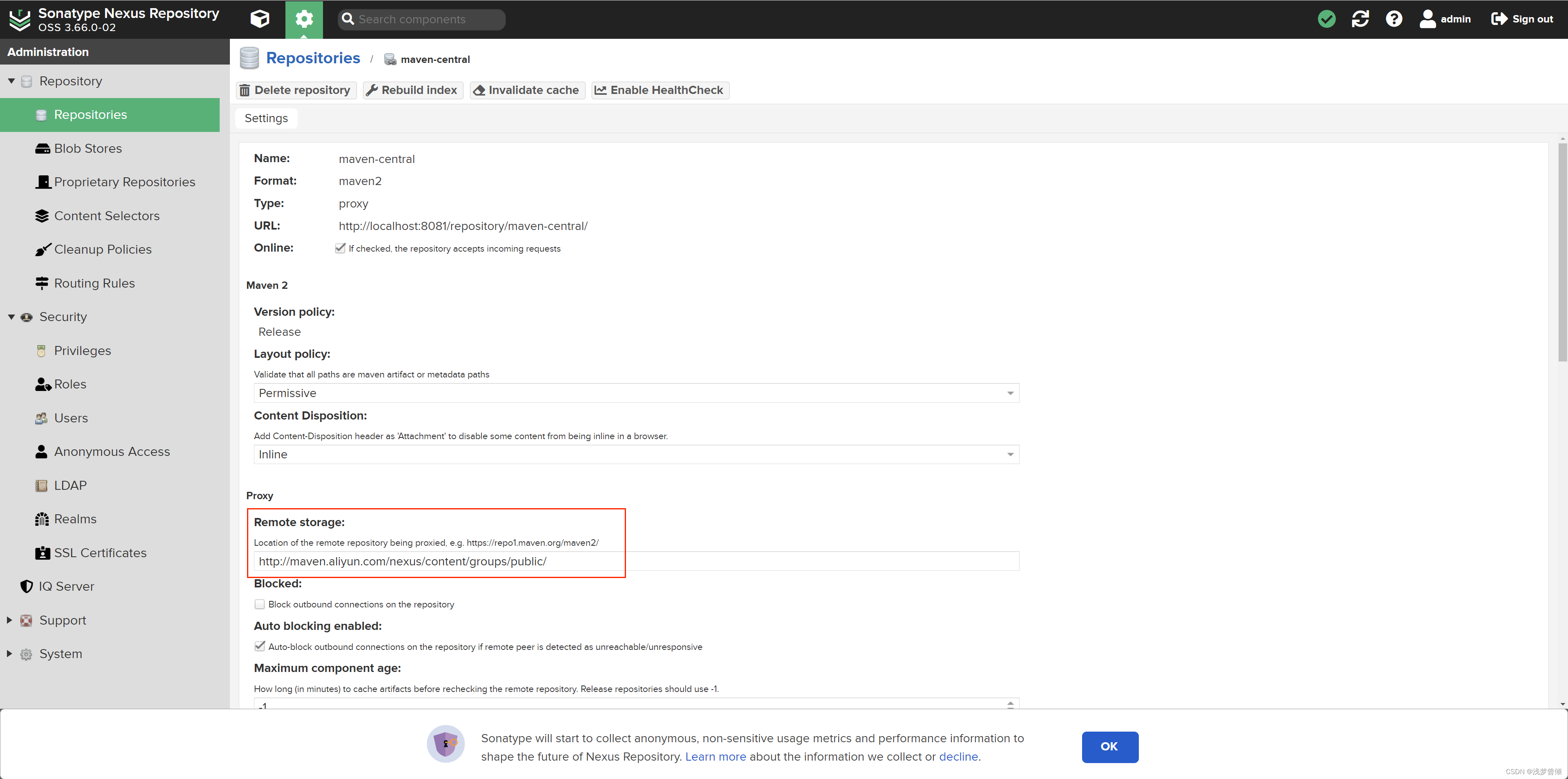
Nexus - Maven私服构建和使用
文章目录 1. Maven 私服简介2. Nexus下载安装3. 如何使用Nexus私服3.1 通过Nexus下载Jar包3.2 将Jar包部署到Nexus3.3 引用别人部署的jar包 1. Maven 私服简介 Maven 私服是一种特殊的Maven远程仓库,它是架设在局域网内的仓库服务,用来代理位于外部的远…...

SpringMVC09、Ajax
9、Ajax 9.1、简介 AJAX Asynchronous JavaScript and XML(异步的 JavaScript 和 XML)。 AJAX 是一种在无需重新加载整个网页的情况下,能够更新部分网页的技术。 Ajax 不是一种新的编程语言,而是一种用于创建更好更快以及交互…...

【数据结构初阶 9】内排序
文章目录 🌈 1. 直接插入排序🌈 2. 希尔排序🌈 3. 简单选择排序🌈 4. 堆排序🌈 5. 冒泡排序🌈 6. 快速排序6.1 霍尔版快排6.2 挖坑版快排6.3 双指针快排6.4 非递归快排 🌈 7. 归并排序7.1 递归版…...

后端八股笔记------Redis
Redis八股 上两种都有可能导致脏数据 所以使用两次删除缓存的技术,延时是因为数据库有主从问题需要更新,无法达到完全的强一致性,只能达到控制一致性。 一般放入缓存中的数据都是读多写少的数据 业务逻辑代码👇 写锁Ǵ…...
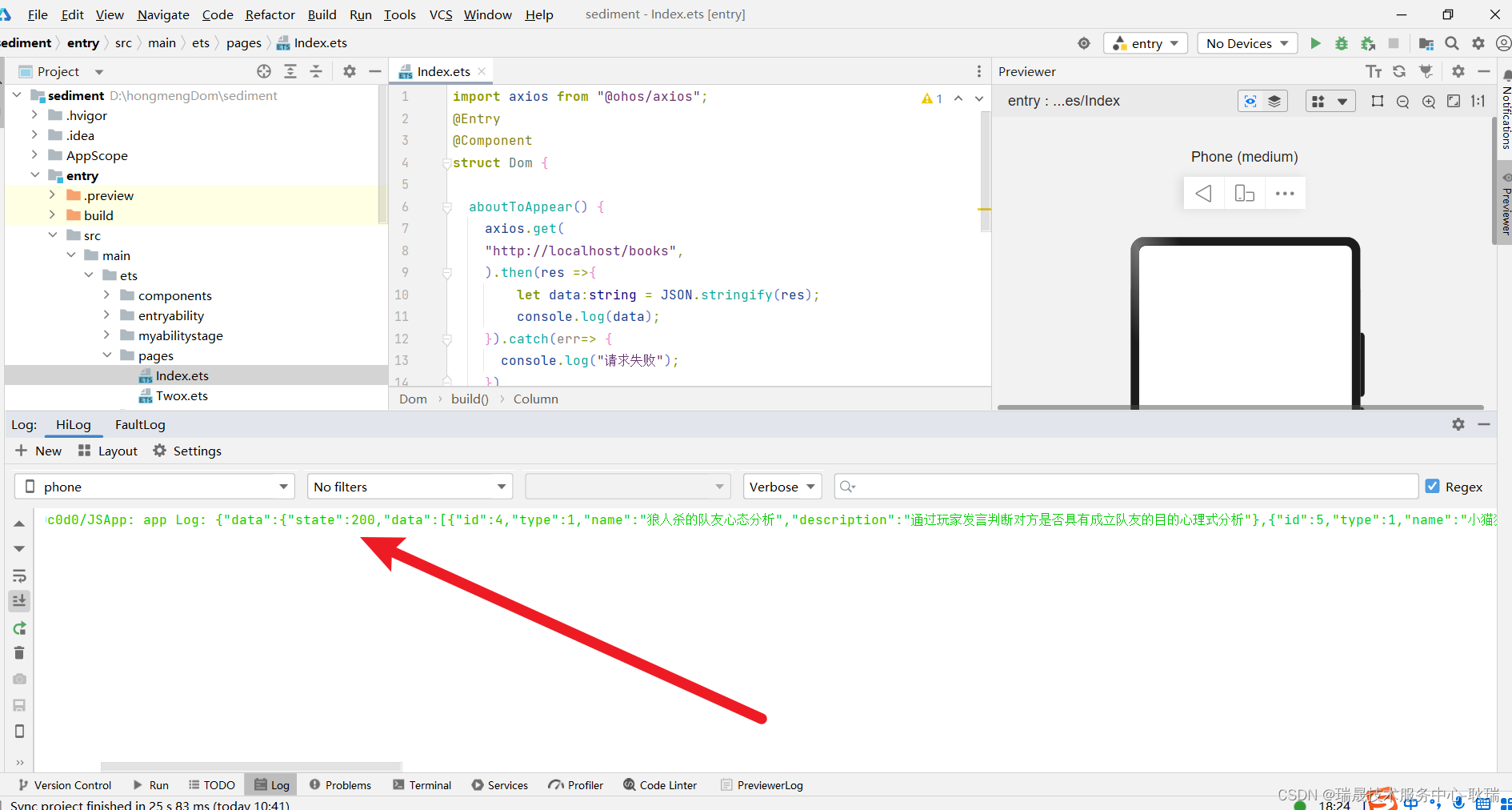
HarmonyOS通过 axios发送HTTP请求
我之前的文章 HarmonyOS 发送http网络请求 那么今天 我们就来说说axios 这个第三方工具 想必所有的前端开发者都不会陌生 axios 本身也属于 HTTP请求 所以鸿蒙开发中也支持它 但首先 想在HarmonyOS中 使用第三方工具库 就要先下载安装 ohpm 具体可以参考我的文章 HarmonyOS 下…...
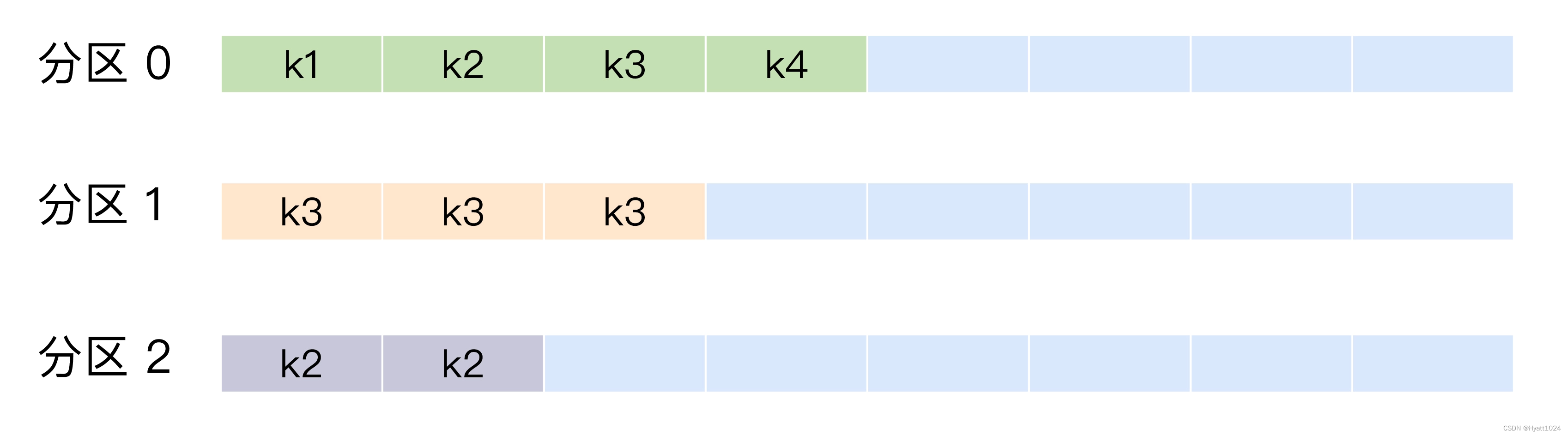
【Kafka系列 08】生产者消息分区机制详解
一、前言 我们在使用 Apache Kafka 生产和消费消息的时候,肯定是希望能够将数据均匀地分配到所有服务器上。 比如很多公司使用 Kafka 收集应用服务器的日志数据,这种数据都是很多的,特别是对于那种大批量机器组成的集群环境,每分…...

【PyTorch】进阶学习:BCEWithLogitsLoss在多标签分类任务中的正确使用---logits与标签形状指南
【PyTorch】进阶学习:BCEWithLogitsLoss在多标签分类任务中的正确使用—logits与标签形状指南 🌈 个人主页:高斯小哥 🔥 高质量专栏:Matplotlib之旅:零基础精通数据可视化、Python基础【高质量合集】、PyTo…...

ocr关键信心提取数据集
doc/doc_ch/dataset/kie_datasets.md PaddlePaddle/PaddleOCR - Gitee.com https://huggingface.co/datasets/howard-hou/OCR-VQA OCR-VQA Dataset | Papers With Code...
Linux中,配置systemctl操作Nginx
最近在通过Linux系统学一些技术,但是在启动Nginx时,总是需要执行其安装路径下的脚本文件,要么我们需要先进入其安装路径,要么我们每次执行命令直接拼上Nginx的完整目录,如启动时命令为/usr/local/nginx/sbin/nginx。 可…...
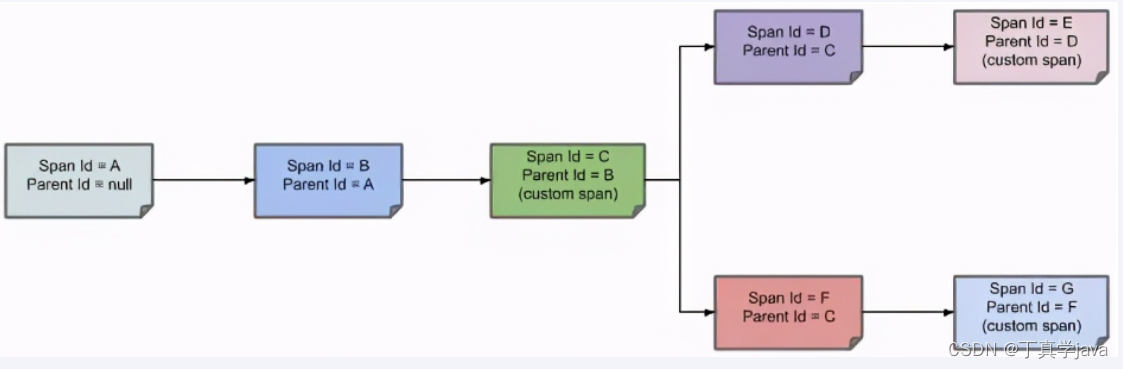
Sleuth(Micrometer)+ZipKin分布式链路追踪
Sleuth(Micrometer)ZipKin分布式链路追踪 Micrometer springboot3之前还可以用sleuth,springboot3之后就被Micrometer所替代 官网https://github.com/spring-cloud/spring-cloud-sleuth 为什么会出现这个技术? 在微服务框架中,一个由客户…...

fanout模式
生产者: public class Provider {public static void main(String[] args) throws IOException {Connection connection RabbitMQUtils.getConnection();Channel channel connection.createChannel();//通道声明指定的交换机 参数1:交换机名称 参数2&…...

Docker基础—CentOS中卸载Docker
要卸载已经安装好的 Docker,可以按照以下步骤进行: 1 停止正在运行的 Docker 服务 sudo systemctl stop docker 2 卸载 Docker 软件包 sudo yum remove docker-ce 3 删除 Docker 数据和配置文件(可选) sudo rm -rf /var/lib…...

深入解读 Elasticsearch 磁盘水位设置
本文将带你通过查看 Elasticsearch 源码来了解磁盘使用阈值在达到每个阶段的处理情况。 跳转文章末尾获取答案 环境 本文使用 Macos 系统测试,512M 的磁盘,目前剩余空间还有 60G 左右,所以按照 Elasticsearch 的设定,ES 中分片应…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...

13.10 LangGraph多轮对话系统实战:Ollama私有部署+情感识别优化全解析
LangGraph多轮对话系统实战:Ollama私有部署+情感识别优化全解析 LanguageMentor 对话式训练系统架构与实现 关键词:多轮对话系统设计、场景化提示工程、情感识别优化、LangGraph 状态管理、Ollama 私有化部署 1. 对话训练系统技术架构 采用四层架构实现高扩展性的对话训练…...
